Free energies for coarse-grained proteins by integrating multibody statistical contact potentials with entropies from elastic network models

Abstract

We propose a novel method of calculation of free energy for coarse grained models of proteins by combining our newly developed multibody potentials with entropies computed from elastic network models of proteins. Multi-body potentials have been of much interest recently because they take into account three dimensional interactions related to residue packing and capture the cooperativity of these interactions in protein structures. Combining four-body non-sequential, four-body sequential and pairwise short range potentials with optimized weights for each term, our coarse-grained potential improved recognition of native structure among misfolded decoys, outperforming all other contact potentials for CASP8 decoy sets and performance comparable to the fully atomic empirical DFIRE potentials. By combing statistical contact potentials with entropies from elastic network models of the same structures we can compute free energy changes and improve coarse-grained modeling of protein structure and dynamics. The consideration of protein flexibility and dynamics should improve protein structure prediction and refinement of computational models. This work is the first to combine coarse-grained multibody potentials with an entropic model that takes into account contributions of the entire structure, investigating native-like decoy selection.

Introduction

One of the most striking properties of globular proteins is their high packing density, observed at both atomics and amino acid resolution. Because of hydrophobic clusters and the network of hydrogen bonds, proteins can be expected (and have been shown) to behave in highly collective ways. Yet, the main tools that are used to assess these structures are pair-wise interactions for energies and local environments for entropies. There is a clear need for more rigorous methods for evaluating the free energies of protein structures. Coarse-grained models of proteins have found favor due to their ability to satisfactorily reproduce results obtained at atomic detail and also their computational speed. This article discusses an investigation of two highly cooperative representations using coarse-grained models: four-body contact potentials for energy and elastic network models for entropy. The latter have been shown through multiple studies that most important motions of globular proteins are the large collective (often domain) motions, indicating that entropy evaluations should be based on the entire structure. Here we propose the integration of these two methodologies to evaluate protein free energies that should offer improvements for the evaluation of protein structure predictions, comparison of structures, and the refinement of computational models of proteins. Success with this approach would improve upon the present parlous state of protein thermodynamic assessment.

Different types of computational protein studies have been performed using knowledge-based potential functions, including structure prediction [1–5], design [6–9], docking prediction [10–13], and folding [14–17]. Atomic [18–20] and coarse-grained potential functions [21–24] have been developed utilizing diverse methodologies. Knowledge-based potentials not only can significantly reduce the computational cost of modeling but can also improve predictions by selecting good predictions from a set. Extraction of better, computationally less expensive coarse-grained potentials that are able to perform as well as atomic potentials is an important challenge in computational biology.

Both coarse-grained and atomic structures use many different types of potentials in assessing protein models and for native structure recognition. The Miyazawa-Jernigan potential [22] is one of the most widely used coarse-grained two-body potentials. However, as suggested by Betancourt and Thirumalai [25], pair-wise potentials are unlikely to be sufficient for threading applications. In principle, multi-body potentials should better account for the more complex three dimensional interactions in densely packed structures, and more importantly, capture the strong cooperativity operative within protein structures. Three-body potentials proposed and developed by Munson and Singh [26] as well as by Li and Liang [27] all showed improvements over two-body potentials. Four-body potentials by Krishnamoorthy and Tropsha [28] (first derived in the context of Delaunay tessellation) also performed better than two-body potentials.

Our group, through a simple geometric construction, recently developed four-body contact potentials [29] incorporating sequence information and details of interactions between backbones and side chains. These potentials also enable us to distinguish between different levels of solvent accessibility for the residues.

Overall performance has been enhanced by combining the four-body sequential [29] with the four-body non-sequential potentials [30] and with a short range potential [31]. The results for the rankings of the best models are obtained by combining these three sets of terms, and globally optimizing the weights for each term based on performance [32].

Four-body contact potentials

Most two-body potentials neglect the sequence information of proteins while both types (sequential and non-sequential) of four-body contact potentials derived by our group [29] consider the interactions between the backbones and side chains and the long-range interactions between side chains. These four-body contact potentials give a more cooperative representation of protein interaction energies and can discriminate well between native structures and partially unfolded or deliberately misfolded structures.

Geometric construction of four-body contacts

Residues are all represented by the geometric centers of the side chain heavy atoms, except for Glycine, where the alpha carbon atom is used.

The geometric construction of four-body contacts is shown in Fig. 1. Three residues form a sequence triplet of a four-body, whose residue types were reduced to eight classes (Table 1). The fourth point in the “4-body” set is the closest nonbonded alpha carbon to the centroid of the three sequential residues. The non-bonded point retains its specific amino acid type as one of the 20 amino acids. Thus a four body set for side chain-backbone interactions always has three sequential points and one non-sequential in the

$$\begin{array}{cc}\hfill P_{4\mid X}& =\frac{\text{number of specific quadruplets given Bu, E, or I in the data set}}{\text{total number of all types of quadruplets given Bu, E, or I in the data set}}\hfill \\ \hfill P_{3\mid X}& =\frac{\text{number of specific triplets given Bu, E, or I in the data set}}{\text{total number of all triplets given Bu, E, or I in the data set}}\hfill \\ \hfill P_A& =\frac{\text{number of specific type of amino acid A in the data set}}{\text{total number of all amino acids in the data set}}\hfill \end{array}$$ (1)

quartet of interacting residues. All possible four body sets are taken into consideration. This is repeated to derive the non-sequential 4-body interactions, where the 4 residues involved are not close in sequence.

Fig. 1.

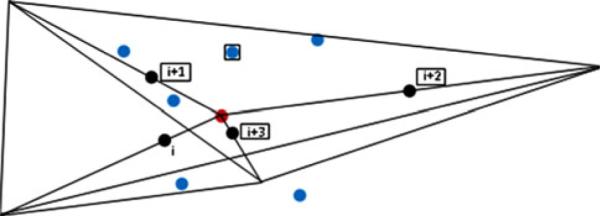
Identification of residue points for use in the four-body contacts. The four black points represent the side chain geometric centers of sequential residues i, i + 1, i + 2, and i + 3. The red point is the geometric center of the four black points which is chosen as the center of the interacting group. The six planes, defined by each of the six combinations of pairs of black points and the central red point, fully subdivide the space surrounding the red point into four tetrahedra. The blue points represent other residues in close proximity to the red point, within the interaction range of 8.0 Å from it. An example of a set of four contacting residues used for potential extraction is shown by the four residues in boxes

Table 1.

The eight classes of residue types chosen to reduce the amino acid alphabet

4-Body class	Residues	Type
A	E, D	Acidic
B	R, K, H	Basic
C	C	Cysteine
H	W, Y, F, M, L, I, V	Hydrophobic
N	Q, N	Amide
O	S, T	Hydroxyl
P	P	Proline
S	A, G	Small

The specific sequence order of the three residues within each backbone triplet is ignored. As a result there are only 120 different triplets instead of 8³ = 512. Data is collected by including the fourth point (one of the 20 types of residues), which is within the cutoff distance (8Å) from the coordinate center (red point in Fig. 1), and assigning it to one of the corresponding four tetrahedra defined by the vectors originating from the red point to three of the black points. Thus, four body sets comprised of the three sequential residues and a non-sequential nearby residue are obtained. This procedure is then repeated for all quartets defining close interacting residues and for the entire set of proteins.

Each of the residues can be fully or partly exposed to solvent when it is on the surface of the protein or buried inside the protein core. These three situations were considered separately for each type of 4-body potential. Relative solvent accessible surface area (RSA) is used to group the triplet into three groups corresponding to buried (with all three residues in the triplet having RSA<20%, denoted as Bu), exposed (with all three having RSA<20%, denoted as E), and intermediate (some of the residues in the triplet being exposed, and some being buried, denoted as I). Better results were obtained in discriminating native structures from a large number of decoys by incorporating surface exposure.

Four-body contact potential energy function

Inverse Boltzmann principle is used to calculate a four-body contact potential energy. First, the probabilities of P_4|X, P_3|X, and P_A, are calculated using the equations shown below. Here P_4|X, and P_3|X are respectively the frequencies of quadruplets and triplets in each of the sets specified by X (=Bu, E, or I) and P_A is the frequency of amino acid type singlets in the protein datasets.

Then, the four-body contact potential energy is calculated using the inverse Boltzmann relationship:

$$E_{4\mid X}=-\mathit{RT}\ln \left(\frac{P_{4\mid X}}{P_{3\mid X}{P}_A}\right)$$ (2)

The total energy for a protein is obtained by summing the four-body contact potential energies over all quadruplets n_q.

$$E_{\text{total}}=\sum _{n_q}{E}_{4\mid X}$$ (3)

This is the equation used to estimate the free energy of native structures and their decoys.

The results are shown in Ref. [29] (see Figure 3 in Ref. [29]) where the relative values of these four-body contact potentials are shown, as a heat map). For these sequential four-body potentials we require the triplet of amino acids to be sequential, but for the non-sequential four-body potentials this requirement is no longer enforced.

Fig. 3.

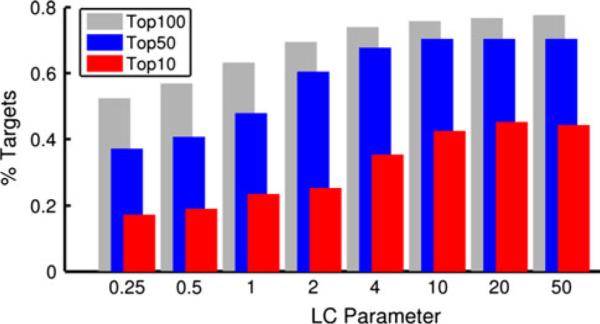
Performance of classification by local character of ΔS. The local character (LC) index is conceptually similar to the metric used in [51, 52], see text and Supplemental Figure 1 for further detail. The percent of targets for which the lowest RMSD decoy appears in the top 10, 50, or 100 is shown. For a parameter value of 4, the LC index has nearly converged to its limit of classification power. From this data, it is evident that ΔS alone is capable of ranking decoys in a meaningful way

Performance of different knowledge-based potential functions has been compared [20, 33, 34] on large data sets of protein models. They have carried out evaluations by finding the success in the ranking of the native structure as the conformation having the lowest energy, and also by obtaining the average Z-score between the energy of the native structure and the next most favorable structure. The Larger the Z-score, the better is the performance.

Performances of different individual potential functions for model ranking

In evaluating the performance of two-body and four-body potential functions in identifying the native (or near native) protein structure CASP8 decoy sets were used. Altogether 23 different two-body (see Pokarowski et al. [35] for details) and four-body potentials (both sequential [29] and non-sequential [30]) were used [32].

All knowledge-based coarse-grained potentials based on coordinates of C^α (sometimes C^β) atoms that are usually designed to capture the statistics of contacts, are tested. For template modeling targets, the BT potential derived by Betancourt and Thirumalai [25] performs best (in terms of correlation coefficients, average Z-score and average RMSD) individually in comparison with other two-body potentials and the two four-body potentials; the best RMSD values being in the range of 4–5 Å [32]. Four-body potentials perform well in the identification of native structures. A few two-body potentials show similar performances with RMSD in the 4 Å range.

The performance for targets from template-free modeling is not as good as that for the homology based targets. However, potentials that perform better for template-free modeling targets also perform better for homology modeling targets but do not yield results that are as good as for the latter. This is due to the fact that the models submitted to CASP8 usually deviate significantly from the native protein structures for the template-free modeling cases, more than for the homology modeling ones, and are usually more poorly packed and/or poorly folded. Therefore empirical potentials which are derived based on real globular protein interactions do not perform well when applied to these cases.

Rankings, RMSDs and correlation coefficients all show that both four-body sequential and four-body non-sequential potentials, on average, perform better than or as well as the two-body potentials [32].

Obtaining an optimized potential

The four-body sequential, four-body non-sequential and short-range potentials were combined linearly using a different weight for each potential according to the following formula:

$$V=w_{4-\text{body}-\text{seq}}{V}_{4-\text{body}-\text{seq}}+w_{4-\text{body}-\text{nonseq}}{V}_{4-\text{body}-\text{nonseq}}+w_{\text{SR}}{V}_{\text{SR}}$$ (4)

An optimization of the weight for each term was performed to find an optimized potential.

The optimization was carried out using the Particle Swarm Optimization (PSO) technique [36]. The weight of the four-body sequential term was set to 1.0 (w_4-body-seq = 1) while the weights for the other two terms (w_{4-body-nonseq} and w_SR) were varied by using the PSO.

For each combination of terms, the average RMSD for the best ranked model and the Z-scores for all CASP8 targets were calculated. CASP8 targets were divided into two subsets according to the method used to generate decoys. One set was comprised of models obtained using homology modeling (153 cases) while the other was obtained from template-free modeling approaches (12 cases).

For the homology modeling targets, the optimized weights obtained for the four-body non-sequential and short-range potentials were 0.28 and 0.22 respectively. For template-free modeling targets, the corresponding weights were different at 1.01 and 0.56.

The native structure rankings obtained for the optimized potential were compared with those obtained for other coarse-grained potentials and for the empirical atomistic potential DFIRE [20]. The Decoys 'R' Us dataset [33] was used for the comparison with the atomistic potential. Both single and multiple decoy sets were used. The weights obtained for homology modeled targets were used in assessing the quality of our optimized potential.

Performance of the optimized potential

The resulting combined potential performs better than the two four-body potentials individually and better than all other coarse-grained potentials (with an average RMSD ~ 3.7 Å for the homology modeling targets using CASP8 decoys), and almost at the same level of performance as the empirical atomistic potentials (using Decoys 'R'Us database). For template-free modeling targets the Betancourt-Thirumalai [25] potentials perform almost as well as the optimized potentials but for homology modeling targets the improvement found for the RMSDs with the optimized potentials is significantly better.

For the misfolded, asilmarh and Pdberr&sgpa data sets from the Decoys 'R'Us database the optimized potentials identify all native structures from these datasets and thereby perform as well as the other empirical atomistic potentials [32] like RAPDF [33], atomic KBP [19] and DFIRE. The native structure ranks and the Z-scores are compared for the above atomistic potentials and for our optimized potentials using multiple decoy sets [32]. Optimized potentials are able to predict all native structures in the lattice-ssfit decoy set, and they fail to identify only two native states in the 4-state reduced decoy set. The average Z-score for the optimized potentials for these decoys is 1.87. Multi-body potentials perform well, if the protein structures are large enough, sufficiently compact, and well-packed with many multi-body contacts.

The explosive growth in the number of protein structures [37], presents many new opportunities. The deeper comprehension of the functional role of a protein requires not only the structure but also information about its dynamics. Dynamics information can be extracted directly from the structures if sufficient numbers of structures of the same protein have been determined [38–40], but these are not so commonly available, and hence, computational approaches are usually used for this purpose. An important lesson from the use of coarse-grained models of proteins is that their motions are dependent on the entire structure, and consequently their entropies should also be dependent on the whole structure. This provides an important new way to extract entropies of protein structures.

Elastic network models

One of the simplest ways to extract dynamics from a static structure is to apply Elastic Network Models (ENM), which employ a simplified energy function together with a coarse-grained representation of the structure. The two major ENM types are the Gaussian Network Model (GNM) [41] and the Anisotropic Network Model (ANM) [42]. Briefly, both of these models represent a structure as a set of masses connected by harmonic springs. Normal modes are calculated from this system which provides information about the dominant motions that are available for the structure. These motions are also the most entropically favored due to the inherent geometry of the conformation. GNM assumes that motion around the native structure is isotropic (Gaussian) and thus does not provide information about the direction of motion, yielding only the magnitude of motion for each point. ANM, on the other hand, yields directional information that is usually referred to as the normal mode shape. For reviews of ENM methods and their use in structural biology, see Refs. [43, 44].

The stiffness matrix describes how resistant to deformation each point in the structure is, within the context of the whole structure and the cooperative interactions within it. In other words, given a deformation with a certain energy (k_BT), the model can be used to determine how far each point will be displaced and, for ANM, in what direction. The GNM stiffness (Kirchhoff) matrix Γ is given by

$$\Gamma =\{\begin{array}{cc}-\lambda \hfill & d_{\mathit{ij}}\le r_c\hfill \\ 0\hfill & d_{\mathit{ij}}>r_c\hfill \\ -\sum _{k=1,k\ne j}^N{\Gamma }_{ik}\hfill & i=j\hfill \end{array}\phantom{\}}$$ (5)

where d_ij is the Euclidean distance between two points, r_c the interaction cutoff, and γ the spring constant. To obtain the mean square fluctuation (MSF) of each point in the structure, the stiffness matrix must be inverted. A pseudo-inverse is computed using Eq. 6 since the stiffness matrix is singular. This is commonly done to compute the mean square fluctuations (MSF), which are related to the B-factors from crystallography.

$${\Gamma }^{-1}=\sum _{i=2}^N\frac{1}{{\lambda }_k}\left(Q_k{Q}_k^{\mathrm{T}}\right)$$ (6)

In Eq. 6, N is the number of points, λ_k is the kth eigenvalue, Q_k the kth normal mode eigenvector, and the superscript T denotes the matrix transpose. The ENMs rely on packing density, a property that plays a key role in the dynamics of biomolecules [45].

If Γ is expressed as Γ = Γ₁ + Γ₂ = Γ₁ − (−Γ₂) where Γ₁ represents the diagonal elements of Γ and Γ₂ the off-diagonal ones, then Γ⁻¹ can be approximated as a Neumann series [46, 47] as

$$\begin{array}{cc}\hfill {\Gamma }^{-1}& ={(I+{\Gamma }_1^{-1}{\Gamma }_2)}^{-1}\times {\Gamma }_1^{-1}\hfill \\ \hfill & =\left[\sum _{i=0}^{\infty }{\left({\Gamma }_1^{-1}{\Gamma }_2\right)}^i\right]\times {\Gamma }_1^{-1}\hfill \\ \hfill & =\left[{\left({\Gamma }_1^{-1}{\Gamma }_2\right)}^0+{\left({\Gamma }_1^{-1}{\Gamma }_2\right)}^1+{\left({\Gamma }_1^{-1}{\Gamma }_2\right)}^2+\cdots \right]\times {\Gamma }_1^{-1}\hfill \\ \hfill & =[I+{\Gamma }_1^{-1}{\Gamma }_2+\cdots ]\times {\Gamma }_1^{-1}\hfill \\ \hfill & ={\Gamma }_1^{-1}-{\Gamma }_1^{-1}{\Gamma }_2{\Gamma }_1^{-1}+{\left({\Gamma }_1^{-1}{\Gamma }_2\right)}^2{\Gamma }_1^{-1}-{\left({\Gamma }_1^{-1}{\Gamma }_2\right)}^3{\Gamma }_1^{-1}+\cdots \hfill \end{array}$$ (7)

where I is the identity matrix. A first order approximation is to replace Γ⁻¹ with ${\Gamma }_1^{-1}$ under the assumption that the ${\Gamma }_1^{-1}{\Gamma }_2$ terms is small. This corresponds to an assumption that the entropy of each point (atom) is independent but provides a simple way to relate it to the freedom of each point. From its definition (Eq. 5) it is evident that Γ₁ contains the degree (number of edges) of each atom along its main diagonal and zeros elsewhere. The degree is often referred to as the atom's coordination number, z_i, as it is a count of the closely packed atoms.

The equation for the change in entropy for point i is computed with the GNM, and the details can be found in Ref. [48]. The basic assumption behind this is that the fluctuations of point i about its mean position obey the Gaussian distribution

$$W\left(\Delta R_i\right)=\text{exp}\left\{\frac{-3{\left(\Delta R_i\right)}^2}{2\langle {\left(\Delta R_i\right)}^2\rangle }\right\}$$ (8)

The corresponding change in entropy is:

$$\Delta S_i=k_B\text{ln}W\left(\Delta R_i\right)=\frac{-\gamma {\left(\Delta R_i\right)}^2}{2T{\left[{\Gamma }^{-1}\right]}_{ii}}$$ (9)

where ΔR_i is the deformation vector representing the changes in positions, T the temperature, k_B the Boltzmann constant, and ΔS_i the change in entropy for the ith point. Upon deformation of the structure, the change in entropy of point i then originates directly from the inverse connectivity of that point (to a first approximation). The deformation is given by the normal mode shape as the deformation vector in Eq. 10, where the amplitude factor, A, can be based on a fixed energy for each mode, the RMSD from the native positions, or by the inverse of the corresponding eigenvalue (the mode's square frequency).

$$\Delta R_k=A{Q}_k$$ (10)

Energy and entropy changes for different structure pairs of the same protein

For the assumption of first approximation by Neumann series given above, there is perfect energy/entropy compensation as seen in the following equation for the change in entropy ΔS_i, and change in energy ΔV_i. Beginning with Eq. 9 we can substitute in the first order approximation ${\Gamma }^{-1}={\Gamma }_1^{-1}$ (Eq. 7).

$$\begin{array}{cc}\hfill \Delta S_i& =\frac{-\gamma {\left(\Delta R\right)}^2}{2T{\Gamma }_{ii}^{-1}}=\frac{-\gamma {\left(\Delta R\right)}^2}{2T\left(\frac{1}{z_i}\right)}=\frac{-\gamma {\left(\Delta R\right)}^2{z}_i}{2T}\hfill \\ \hfill & =\left(\frac{\gamma }{2T}\right){\left(\Delta R\right)}^2{\Gamma }_{ii}=\frac{-\Delta V_i}{T}\hfill \end{array}$$ (11)

where the coordination number of point i is z_i. Also, note that the spring constant γ used is arbitrary and usually set to 1, and the change in potential energy is that of a Hooke's law spring $\Delta V=\frac{\gamma }{2}\Delta R^2$. Since the change in free energy is

$$\Delta G=\Delta V-T\Delta S$$ (12)

the contributions from energy and entropy terms to the free energy change are exactly equal. In Dubois et al. [46] we find that the Neumann series approximation will hold if the largest magnitude eigenvalue of ${\Gamma }_1^{-1}{\Gamma }_2$ is less than 1. For the 10 structures initially considered (see Table 2) we find that the largest magnitude eigenvalue is exactly equal to 1 and that the expansion may not converge. For these reasons we will use the pseudo-inverse definition given by Eq. 6.

Table 2.

Five structure pairs from the MolMovDB database [49]

Structure pair	PDB 1	PDB 2	N
Biotin carboxylase	1DV1A	1DV2A	433
ATP sulfurylase	1I2DA	1M8PA	573
Elongation factor 2	1N0VC	1N0UA	842
Adelylate kinase	1AKEA	4AKEA	214
Acetyl-CoA-synthasea	ACS1	ACS11	728

Four letter PDB IDs are given as well as the chain ID from the structure

^aFor this structural transition, no PDB files were listed. Instead, we chose the first and last frame (1 and 11) from the morph. N is the number of matching residues between the two structures

Our initial exploration of the energy and entropy relationship from the ENMs utilizes five structure pairs from the database MolMovDB [49]. This is a database of known conformations and computed interpolations between structures that employs a short range energy minimization for each intermediate structure to attain feasible conformations. The protein names, PDB IDs, and the number of residues are given in Table 2. The changes in potential energy for each point ΔV_i are calculated by assuming that each point moves independently in a given normal mode. That is, we initially calculate the amplitude that will deform the structure by k_BT energy, i.e., thermal energy. A temperature of 300 K was used for all calculations. From this deformation, we then calculate the potential energy change for each atom assuming all others remain fixed. We calculate the deformations based on the entire structure experiencing the thermal background energy. The change in entropy for each point in the ENM was calculated using Eq. 9 with the pseudo-inverse defined in Eq. 6.

We calculate the effect of deforming the structures based on the three lowest frequency normal modes, and the results are summarized in Table 3. For each normal mode used, we deformed the structure so that the total change in potential energy is k_BT. The mean change in potential energy is estimated here with the GNM, which does not have directions of motion, so this may not be so precise and may overestimate the energetic contribution to ΔG (which is defined in Eq. 12). Despite this, the entropic changes still amount to 20–50% of the free energy changes.

Table 3.

Sum of changes in entropy and energy upon deformation by the first three normal modes

PDB	$\sum _{i=1}^3-T\times \overline{\Delta S^i}$	$\sum _{i=1}^3\overline{\Delta V^i}$	% S
1DV1A	0.202	0.350	41
1DV2A	0.203	0.250	46
1I2DA	0.233	0.780	24
1M8PA	0.248	1.060	23
1N0UA	0.243	0.840	23
1N0VC	0.243	0.840	30
1AKEA	0.155	0.290	35
4AKEA	0.187	0.550	26
ACS1	0.226	0.390	36
ACS11	0.210	0.270	45

The effect of deforming the structure by the first three modes is summed. The rightmost column is the average percent of the total change in the entropic component of the free energy. All modes are assigned k_bT total energy for their deformation

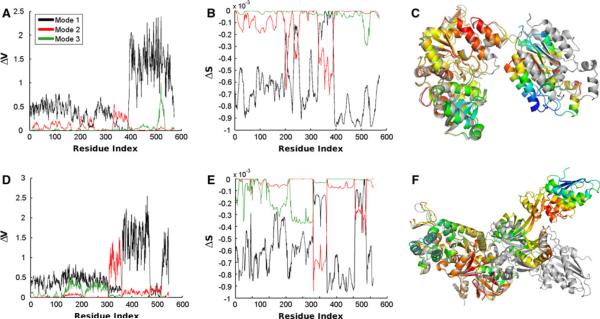
Figure 2 compares the change in energy (a) and entropy (b) upon deformation by the first three normal modes for the ATP sulfurylase structure 1I2DA (structure shown in panel c). We show the entropic change on the structure corresponding to mode 1. Coloring is spectrally, from red, to yellow, to green, and finally to blue. The red side of the spectrum corresponds to zero and blue to the largest change in entropy. The structure 1M8PA is shown in gray. This structure pair is the most similar of the five. d, e, and f of Fig. 2 are similar to a–c, but for the elongation factor 2 structures and panel f shows the structure pair 1N0VC. This structure pair has the largest total RMSD of the five pairs. In both examples, we find that the part of the structure that requires the largest fluctuations to attain the other conformation also has the largest change in entropy in the first mode of motion.

Fig. 2.

Comparison of the change in energy and entropy upon deformation by the first three normal modes. a–c Data is shown for the ATP sulfurylase structure 1I2DA. c We show the entropic change on the structure corresponding to mode 1. Coloring is spectral from red, to yellow, to green, and finally to blue. The red parts correspond to zero and blue parts to the largest change in entropy. The structure 1M8PA is shown in gray. This structure pair is the most similar of the five. Parts d–f are similar to a–c, but for the elongation factor 2 structures and in f is shown the structure pair 1N0VC. This structure pair has the largest total RMSD of the five pairs

In Table 4 we show the differences in energy and entropy between the structure pairs for the slowest global mode of motion. Differences in entropy and free energy changes between the structure pairs do not appear to relate closely to either the sizes or the RMSD changes (shown computed in two different ways). This is possibly because in this exploration we are considering only the single difference between two structures whereas each of the individual structures should be more properly represented as an ensemble of conformers. The background energy here is simply taken as k_bT at T = 300, or about 0.6 kcal/mol. In calculating the amplitude of deformation we have scaled the total deformation to be k_bT in one normal mode. Normal modes represent the natural vibrational frequencies of the structure.

Table 4.

The mean difference in computed energy (V) (ENM), entropy (S), and free energy (G) for the five structure pairs

Structure pair	Δ V	– T Δ S	Δ G	RMSDCE	RMSDTotal
Biotin carboxylase	0.087	0.003	0.165	4.17	11.48
ATP sulfurylase	−0.253	0.011	0.271	2.63	6.41
Elongation factor 2	0.226	−0.034	0.267	2.49	23.61
Adenylate kinase	−0.188	0.034	0.256	3.57	9.35
Acetyl-CoA-synthase	0.093	−0.034	0.339	5.14	8.06

Entropy is calculated using Eq. 9 with the pseudo-inverse defined in Eq. 6. Equation 12 gives the change in free energy. RMSD_CE is the root mean square deviation returned by the CE algorithm for superimposing the two structures. It is thus the RMSD of the aligned section. RMSD_Total is the RMSD of all matching alpha carbons. In this case, matching is for the residues chosen for comparison. For example, the two biotin carboxylase structures have 433 and 450 residues. We choose for comparison the 433 residues that most closely match after alignment with CE

In Tables 3 and 4 we report the average change in entropy across all residues in the structure, whereas in Table 5 we calculate the total entropic contribution to free energy. Combined with the average change in contact potential energy, average changes in residue entropy provides insight into the relative contribution of energy and entropy for each deformation of each structure. Within the ENM framework, we can see from Table 3 that the entropic contribution to free energy is significant. Thus, the development of better methods to take into account entropic as well as energetic contributions is needed. In Table 5 we present a first look at combining contact potentials for energetic evaluation with entropy calculations from ENMs. The entropy values compared here are difference in the total free energy change of entropic origin if the structure was influenced by all three of the lowest frequency normal modes. That is, we first compute

$$\Delta S_T=\sum _{k=1}^3\sum _{i=1}^N\Delta S_{ki}$$ (13)

for each of the structure pairs, where k indexes the mode and i the residue. The difference in ΔS_T between the structure pairs is reported and indicates the difference in total entropy change upon excitation of the first three modes.

Table 5.

Free energy changes by combining the optimized four body energies with the entropies estimated from the elastic network model. The corresponding RMSDs are in Table 4

Structure and PDB IDs	Δ E	– T Δ S	Δ G
Biotin Carboxylase (1DV1A-1DV2A)	−14.6	−2.8	−17.4
ATP sulfurylase (1I2DA-1M8PA)	−12.4	−6.3	−18.7
Elongation Factor 2 (1N0UA-1N0VC)	−15.1	26.9	11.8
Adenylate Kinase (1AKEA-4AKEA)	5.5	−7.2	−1.7
Acetyl-CoA-Synthase (ACS1-ACS11)	−8.2	24.6	16.4

Inspection of the results in Table 5 show some interesting features. In the case of biotin carboxylase the structures are with and without ATP bound. The contact potentials show a lower energy for the ATP bound form and also that the ATP bound form has a negative entropic contribution. Likewise for ATP sulfurylase the T state has both lower energy and lower entropy than the R state. For elongation factor 2, the inhibitor bound form is favored energetically but not entropically, presumably because of tight binding that reduces conformational freedom. The two adenylate kinase structures are open and closed. The energy favors flap closing but entropy disfavors closing. However, the net free energy difference between open and closed forms is quite small, perhaps pointing to the relative ease of this structural transition. For acetyl co-A synthase the transition is favorable energetically but is overall unfavorable because of a large unfavorable entropy change.

The ENMs are entropic models that depend on the shape and packing density of the modeled structures. They can be used to extract entropic changes for the various deformations of the structure. The energies used for the exploration in Table 4 are not fully reliable. The entropies computed here can, however, be combined more reliably with energies from pair-wise, 4-body [29], or distance dependent potentials [50] to provide a better understanding of protein structural energetics and their dynamics. This has been done in Table 5. Also, it would be possible to generate ENM models using all atoms, this approach could allow comparison and evaluation with commonly used atomic force fields such as AMBER or CHARMM to increase the accuracy, specificity, and breadth of the free energy analyses.

The inclusion of ΔS in the calculation of ΔG is used to improve two aspects of structure prediction. First, the more standard metric of structure prediction is compared in Fig. 3 using the CASP9 dataset, where the target sequence is modeled as a monomer and we use ΔS alone as a classifier for decoys being native-like. Testing numerous aspects of the ΔS profiles, we find that a local character index (LC) similar in concept to the metric used by Brooks et al. [51] and Lu and Ma [52] provided the best classification based on the number of times we find the decoy with lowest RMSD to the target in the top 10 ranked decoys. The LC index used here is computed as LC = Σ(ΔS^1/ρ), where ρ is the LC parameter. In the following, ΔG is always normalized by the number of residues in the decoy.

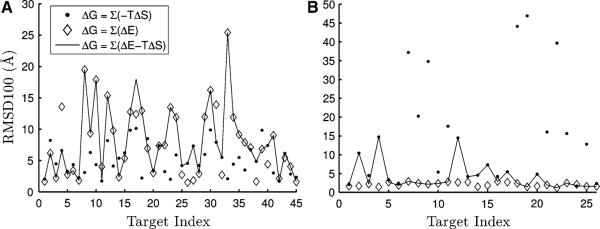
In Fig. 4 a comparison between ΔE (from 4-body potentials), ΔS, and ΔG for classification of decoys is made. For clarity, we denote changes in potential energy from the ENM as ΔV and energetic changes calculated from the 4-body potentials as ΔE. An important initial point is the lack of convergence in decoy prediction as judged by the range of RMSD100 values in Supplemental Figure 2. The RMSD100 is a normalized RMSD proposed in Ref. [53] and is interpreted as the RMSD between two 100 residue proteins of equivalent similarity to the structure pair in question. Some targets have no decoys within 5Å RMSD100. Utilizing the energy or entropy alone, we achieve an average classification accuracy of 10.5 and 17.1Å, respectively, across all targets. By combining the two metrics into one classifier, the average RMSD100 remains at 10.5Å. This is due to increased performance for some targets, but decreased performance for others (Fig. 4), showing that the entropic contribution to ΔG upon mode motions is meaningful for structure prediction, but our present treatment is likely still too simple. In this case, we observe in Fig. 4 that ΔS performs poorly for some targets, but significantly outperforms ΔE for others. These tests were performed on 110 out of the 129 published CASP9 targets. We report RMSD100 values, but the CASP typically uses a Z-score describing the significance of the structure alignment. The Z-score is more lenient for unpredicted parts of a structure. For instance, most of the RMSD100 values that are over 50Å are due to the decoy containing a long (mostly linear) terminus. These extended termini are residues that were not significantly modeled, but were retained in the deposited prediction so that the sequence would match that of the target. Their inclusion in RMSD-based comparisons may be misleading. See Supplemental Figure 4 for a listing of the RMSD for the best decoy for each target. The dataset was limited by the resolution of the resolved experimental structure, presence of oligomeric state prediction (see below), and size of the target sequence.

Fig. 4.

Result of classifying CASP9 monomer decoys using entropy, energy, and a free energy. a The 45 targets that have the lowest ΔG calculated using only ΔS are selected. We plot the RMSD to the native structure of the decoy with lowest ΔG as calculated using only ΔS (filled circle), only ΔE (open diamond), and a combination (dash) using δ = 1 in Eq. 14. For these targets, ΔS outperforms ΔE yielding a mean decoy RMSD100 of 5.2 and 7.9 Å, respectively. The combined method does not significantly outperform the 4-body potential for these targets. b A similar plot, but now the 26 targets with the best classification using only ΔE are shown. For these structures, the 4-body potential significantly outperforms the entropy and combined classification, with mean RMSD100 of the lowest RMSD decoy of 2.1, 14.5 and 4.0 Å, respectively. Other interesting patterns emerge for different subsets; see text for details

Across most subsets considered, there were no size or “presence of good decoy” effects seen. The latter refers to the case where a target has no decoy within 5Å RMSD. An interesting exception is when the targets are limited to those where the ΔG of entropic origin is below a threshold—then there is a strong correlation between the presence of native-like decoys and the computed ΔG. For instance, if the threshold is set to −1, the correlation of the RMSD of the most native-like decoy with either ΔE or ΔS is 0.69 and 0.53, respectively. Such a metric might be useful to determine whether a set of decoys contains any native-like predictions and if so, how native-like they are likely to be.

We also perform a test using a newly available metric—oligomeric state prediction. In the most recent CASP competition, contributors had the option of predicting not only the structure of target sequences in monomer form, but also of the higher order oligomers. In our dataset there are a total of 65 monomers, 33 dimers, 4 trimers, and 8 tetramers, as determined by the experimentally determined structure corresponding to the CASP9 target sequence. Correspondence between the target and decoy structures was obtained using the Smith-Waterman [54] local alignment algorithm and a low gap opening penalty to allow for unresolved loops in the crystal structure or parts of the sequence not modeled by the decoy. Following sequence alignment, a structure alignment between reasonable pairs was performed and normalized using the RMSD100 metric of Carugo and Pongor [53]. For all combinations of ΔS and ΔE, the monomer predictions are correctly identified because these structures were never predicted to occupy higher oligomeric states. Using only energetic contributions to ΔG, we obtain an average classification index of 2.0, 5.3, and 1.0 for dimers, trimers, and tetramers, respectively. If the entropic contribution is used alone, the average classification index moves to 3.0, 4.5, and 7.1—worse for even numbered oligomers. If the two contributions are combined in equal proportion, an improved classification index of 1.9, 5.3, and 1.0 is obtained. Scale values (δ) from 0 to 100 in increments of 0.1 were tested which relate the contribution to ΔG of ΔE and ΔS by:

$$\Delta G=\Delta E-\delta \mid \overline{\Delta E}∕\overline{\Delta S}\mid k_{B}T\Delta S$$ (14)

The prediction values listed previously were for δ = 1 and are quite similar for δ ≤ 1.8. However, for δ > 1.8, there is improved accuracy for trimer predictions (to 4.5Å), and decreased performance for even numbered oligomeric states. Interestingly, these minor gains in monomer and oligomeric state prediction point to the possibility of improving evaluations of protein thermodynamics by utilizing information from the entire structure.

There are a number of aspects of ΔG that are not yet accounted for. For instance, in calculating ΔE, the theory applied here assumes that the contribution is a change in energy from a disordered state to the folded state. However, the entropic contribution to free energy is computed as the change in entropy upon excitation of the normal modes. A more accurate model for the inclusion of the entropic penalty for folding (entropy of the denatured state) might yield a ΔS that is more comparable to the ΔE computed by the 4-body potentials and improve oligomeric state prediction and decoy selection in the future. A further consideration is the change in molecular volume. For heat pumps, engines, and many other objects the change in internal energy is often calculated in a way that takes into account the work done by changes in pressure and volume within the system. This aspect of entropy is usually ignored for protein systems, but must be a contributor as the compactness (volume) of a protein changes upon folding. Also, a protein structure exists as an ensemble of structure sampling from the feasible motions. As the structure samples conformations it also may change the molecular volume, which could be another contributing factor.

The proposed integration of statistical contact potentials with elastic network models of proteins will potentially improve coarse-grained modeling of protein structure and dynamics. The consideration of protein flexibility and its fluctuation dynamics should improve protein structure prediction, and should lead to a better refinement of computational models of proteins, demonstrated here to improve the selection of native-like decoys.