Abstract
A significant problem in the study of Pavlovian conditioning is characterizing the nature of the representations of events that enter into learning. This issue has been explored extensively with regards to the question of what features of the unconditioned stimulus enter into learning, but considerably less work has been directed to the question of characterizing the nature of the conditioned stimulus. This paper introduces a multilayered connectionist network approach to understanding how “perceptual” or “conceptual” representations of the conditioned stimulus might emerge from conditioning and participate in various learning phenomena. The model is applied to acquired equivalence/distinctiveness of cue effects, as well as a variety of conditional discrimination learning tasks (patterning, biconditional, ambiguous occasion setting, feature discriminations). In addition, studies that have examined what aspects of the unconditioned stimulus enter into learning are also reviewed. Ultimately, it is concluded that adopting a multilayered connectionist network perspective of Pavlovian learning provides us with a richer way in which to view basic learning processes, but a number of key theoretical problems remain to be solved particularly as they relate to the integration of what we know about the nature of the representations of conditioned and unconditioned stimuli.
Keywords: Connectionist models, Multimodal processing, Conditional Discrimination learning, Sensory-Specific Associations
Early theories of learning focused on the question of associative structure, e.g., whether learning was best described in terms of stimulus-stimulus (S-S) or stimulus-response (S-R) associations. Although much progress had been made on that problem with the innovative ideas of Tolman (in introducing the reinforcer revaluation test), this issue became seemingly intractable in mid 20th century psychology to a large extent because theorists of different persuasions were unwilling to reach a consensus as to what counted as basic evidence for or against a given approach (see Kendler, 1952, but also see Rozeboom, 1958). It is, perhaps, no surprise, then, that subsequent major developments in learning theory occurred with the advent of quantitative models of basic learning processes that were entirely agnostic with respect to the question of associative content (e.g., Mackintosh, 1975; Rescorla and Wagner, 1972). Theorists realized that whatever the elements were that became associated there was much merit behind the notion that the associative process itself could be understood in isolation. This had the important effect of side stepping a potentially highly theoretically charged quagmire of arguments over issues of associative content.
Although this general approach was important in a historical context, more recent advancements in learning theory have led to a more integrative understanding of basic learning processes where a reasonable consensus has been reached concerning evidence for different forms of associative content. Moreover, there is also growing recognition that adequate theories of learning must simultaneously consider issues of associative content together with a quantitative description of the process. The clearest example of this is probably the AESOP theory of Wagner and Brandon (1989) that recognizes that certain types of data can most readily be understood only when fractionating learning into its different emotive and sensory contents. These two prevailing sentiments bode well for the development of more complete theories of basic learning processes.
Another example comes from Konorski’s (1967; see also Pearce & Hall, 1980) description of Pavlovian learning as a connection between mental representations of conditioned and unconditioned stimuli (CS and US, respectively). This view (depicted in Figure 1) has come to be known as the “standard model of associative learning” (e.g., Hall, 1996; 2002). Mental representations of the CS and US can be depicted as separate nodes within a simple computational architecture or “neural net,” and, indeed, a great deal of research has gone into characterizing the rules for adjusting the connection weights between such nodes. However, although this general depiction of Pavlovian learning does emphasize that learning is to be construed in terms of an association between two stimulus events, it is far from clear just what is the nature of the mental representations of those stimulus events (i.e., of CS and US).
Figure 1.

The standard view of Pavlovian learning posits that learning consists of connections forming between representations of conditioned (CS) and unconditioned (US) stimuli. The arrow denotes the direction of this associative connection.
The main goal of this paper is to offer some thoughts on the nature of the CS and US representations that develop during Pavlovian conditioning. Regarding the ‘nature of the CS’ question, I will first consider some of the behavioral phenomena that I think have critical implications in addressing this question. Then I will offer a connectionist learning framework that does a reasonable job of capturing the main facts considered here. Regarding the ‘nature of the US’ question, I will first provide a sketch of a framework for thinking about learning involving multiple attributes of the US, selectively review some of the data illustrating learning involving those different US attributes, and then consider research that addresses the important question of the potential independence of learning involving those distinct US attributes. Finally, I will conclude by offering some final comments regarding the importance of examining the questions of the nature of CS and US representations.
Nature of the CS
Traditional models of Pavlovian learning have had little to say about the question of the nature of the CS (e.g., Rescorla and Wagner, 1972). Once a stimulus has been processed and gains access to the associative learning system, then modifications in the associative strength connecting two events is commonly thought to take place. Just how the CS reaches this learning system has, by some accounts, been immaterial for an accounting of the associative learning process itself. However, as was pointed out by Rescorla (1980), and more recently by others, the organism very likely learns to represent the conditioned stimulus as well as the associative relation between the CS and US. Early work on within-compound conditioning highlighted the importance of this (e.g., Rescorla, 1980). However, there are a number of ways in which one can imagine how modifications in the CS representation might take place as a result of learning, and each way may have very different implications for understanding associative learning phenomena of interest.
It is worth distinguishing two very different sorts of answers to this general question of how the organism learns about the stimulus. On the one hand, there are models having to do with fairly low-level experience-dependant changes in sensory and attentional processing of the stimulus, and, on the other hand, there are models asserting rather higher-level experience-dependent changes in what may be referred to as the perceptual and conceptual processing of the stimulus. The basis for this distinction is where learning is assumed to take place within the associative circuitry. When modifications in learning take place at an initial layer of processing I refer to this as involving “low-level” changes. In contrast, as will be seen shortly, learning may also take place at a “hidden-layer” of processing that exists between input and output layers. I refer to changes at this hidden layer as involving “higher-level” changes in stimulus processing because when such changes occur it results in a recoding of the input representations at this somewhat deeper “hidden” layer.
The first type of model is well exemplified by the theories of Blough (1975), Mackintosh (1975), Pearce and Hall (1980), Wagner (1978), Pearce (1987; 1994; 2002), Wagner and Brandon (2001; see also Wagner, 2003; 2008), McLaren and Mackintosh (2000; 2002), and Harris (2006). Although these theories differ in many ways from one another, one commonality is the assumption that experience produces changes in the manner in which the stimuli are initially processed. Specific assumptions in this regard differ in whether attention to distinct stimulus features varies with experience (Harris, 2006; Mackintosh, 1975; Pearce and Hall, 1980; Wagner, 1978), whether stimuli are represented in terms of configural processes (Pearce, 1994; Wagner and Brandon, 2001), or whether the representation of stimuli change with experience as a function of detailed interactions among component elements that define the stimulus (Blough, 1975; McLaren and Mackintosh, 2000; 2002; Wagner and Brandon, 2001).
In contrast, another set of theories focus on experience-dependent changes in the stimulus that occur at a deeper level within the processing system. Characteristic of this class of theories are the neural network models of Gluck and Myers (1993), Schmajuk and DiCarlo (1992; see also, Schmajuk, Lamoureux, and Holland, 1998), Kehoe (1988), and Honey (2000; see also Honey and Ward-Robinson, 2002; Honey, Close, and Lin, 2010). Each of these models has in common the idea that conditioned stimuli are represented at an initial processing stage by distinct low-level features. However, neural network approaches additionally assume that these low level stimulus features then receive further processing in a system whose processing elements are initially independent of the input features, the so-called “hidden layer” of processing elements. Over the course of training, an internal representation of the stimulus “emerges” from the new connections established between input level features and elements of the hidden layer. Furthermore, these internal representations of the stimuli are additionally assumed to enter into associations with output level representations that include representations of the US. The idea that internal representations of stimuli change with experience and play a fundamental role in cognition has its origins in the parallel distributed processing models of cognition in the 1980s (see Rumelhart, McClelland, and the PDP research group, 1986).
Figure 2 depicts the main distinction between these two classes of model. It shows that stimulus representations depend, on the one hand, on changes at the input layer (Panel A) or at a more internal layer (Panel B). In both cases, stimuli (CS1, CS2, CS3, etc) are assumed to activate sets of sensory features (a, b, c, d, etc). Similarity among stimuli can be coded in different ways, but one simple way is to assume that similar stimuli activate features that may be specific to a particular stimulus or that may be activated by multiple stimuli (e.g., feature a versus feature b). Models of the type shown in Panel A differ in their assumptions regarding the nature of the interactions among features, but all construe learning in terms of new connections forming directly between stimulus features and the US, as well as new connections among the features themselves. In Panel B a basic connectionist network architecture is presented in which stimuli are also coded in terms of the sets of sensory features they activate. However, learning in this situation is construed in terms of two types of learned connections. New connections can be established between the initial sensory feature layer and the hidden layer of processing units, and also between the hidden layer of processing units and the outcome or US layer. As noted above, changes in input-hidden layer connections result in the stimuli becoming re-coded at the hidden layer by the particular hidden layer activation patterns obtained when different stimuli are presented. It makes sense to think of this as involving “perceptual” or “conceptual” changes in the stimulus representation because initially these hidden layer units play no special role in representing the physical stimulus. Their role is governed by experience-dependent changes in input-hidden layer connections that ultimately result in stable hidden layer activation patterns when a stimulus is presented. The representation of the stimulus truly emerges from these changes in connection strengths. Thus, so-called higher-level representations of stimulus configurations, stimulus categories, or of abstract representations (e.g., various sequential dependencies among cues) may emerge at this level. Learning between the hidden layer and outcome layer can then be thought of as involving new associations between internal representations of stimuli and the US.
Figure 2.
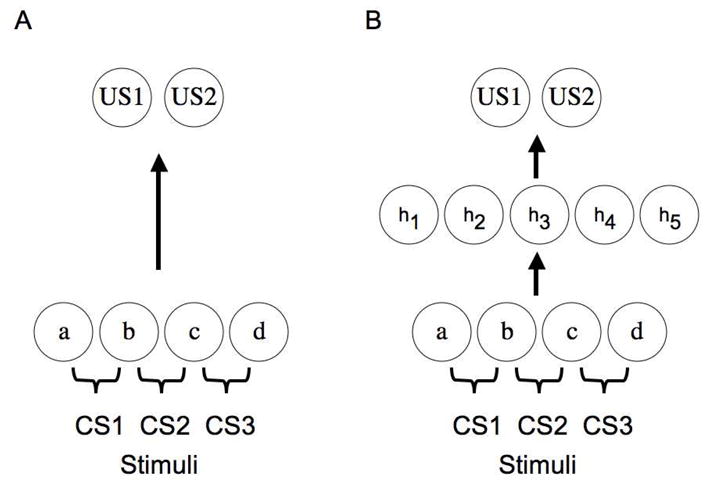
Panel A depicts a simple connectionist network where conditioned stimuli (CS1, CS2, CS3) activate low-level stimulus features (a, b, c, d) and learning involves changes in connection weights between this feature layer and an output layer consisting of unconditioned stimuli (US1, US2). Panel B depicts a more complex connectionist network where stimulus features activate unconditioned stimuli by first activating a hidden layer of units (h1, h2, h3, h4, h5). Learning takes place from feature to hidden and hidden to US layers.
Phenomena Most Relevant to a Hidden Layer Approach to Perceptual Representations
Is there any empirical evidence that might point to an associative network approach that goes beyond the standard model by including a level of representational elements at some hidden layer intermediate between input and output layers? This question has received some but not an extensive amount of attention in the literature. Models of this general sort are well known for their ability to solve complex conditional discrimination learning problems, especially so-called non-linear problems. Examples of this class of problems include biconditional, negative patterning, and ambiguous occasion setting discrimination learning. However, although all of the models cited above can, in one way or another, provide an account for these sorts of discrimination learning phenomena, not all of the models do so in accurate ways. For instance, Pearce and his colleagues have collected an extensive amount of data pointing to shortcomings of the Rescorla-Wagner model in accounting for many of these phenomena (e.g., Haselgrove, Robinson, Nelson, & Pearce, 2008; Pearce, Esber, George, & Haselgrove, 2008; Redhead and Pearce, 1995). At the same time, the configural model advanced by Pearce has difficulties of its own. One particularly striking problem is that it fails to account adequately for the basic difference that animals routinely display in mastering feature positive versus feature negative discriminations. The basic “feature positive effect” as it has sometimes been called (e.g., Hearst, 1984; Jenkins and Sainsbury, 1969) is a very robust effect in which animals solve a feature positive discrimination (e.g., AB+, B−) much more rapidly than a feature negative discrimination (i.e., AB−, B+). Since the Pearce model (Pearce, 1987; 1994; 2002) assumes that similarity between compound and element is symmetrical it predicts that discrimination learning in these two tasks should proceed at identical rates. However, if the experimental context is also assumed to play a role, then this model can predict a very slight advantage in learning the feature positive discrimination. But even under these circumstances, the advantage for the feature positive discrimination is meager even after allowing the context salience to be set to the unreasonable level of 5 times greater than the salience of the discrete stimuli. Thus, this model fails to adequately capture the robust difference that researchers have often observed when animals learn these two tasks.
Another class of phenomena that more uniquely suggests a hidden layer perspective is variously referred to as “acquired equivalence and/or distinctiveness of cue effects” or “common coding effects.” One excellent experiment that illustrates the basic issues is that of Honey and Hall (1989). In this experiment rats initially learned to associate two auditory stimuli with a food pellet and to discriminate these from a third auditory stimulus that was presented without food. In a subsequent phase, one of the food-associated auditory stimuli was then presented without food and paired with foot shock, thus establishing a fear response to that auditory cue. At issue was the extent that this new fear response would generalize to the other two remaining auditory stimuli. In this test the rats displayed more fear to the other auditory cue that was also paired with food in the first phase, suggesting that, in some sense, the two food-paired cues had become “equivalent” (or that the two food cues had become “distinctive” from the non-food cue). Although various mechanisms have been offered to explain results like these perhaps the most reasonable account is the representation-mediated explanation offered by Honey and Hall (1989; also Hall, 1996). According to this view the food-paired cue evoked a representation of the food pellet during the time it was paired with shock, and this resulted not only in the formation of an association between the auditory cue and shock but between the pellet representation and shock as well. When the other food-paired cue was presented during the test session, it, too, evoked this pellet representation, and its association with shock resulted in greater generalization of fear compared to the other auditory stimulus.
Although this account is appealing and there is much evidence to support it (see Hall, 1996; Kerfoot et al., 2007), the mechanism cannot explain all instances of acquired equivalence and/or distinctiveness of cue effects. These other effects more strongly point to the involvement of a deeper level of stimulus processing illustrated by the hidden layer neural network in Figure 2B. For instance, Delamater (1998; see also Delamater, Kranjec, & Fein, 2010) reported that rats were better able to discriminate between two stimuli within the same sensory modality if those stimuli were previously paired with distinctive outcomes (pellet and sucrose) as opposed to the same outcome. The representation-mediated account could explain this finding by assuming that during discrimination learning each stimulus evokes a distinct outcome representation and these are differentially paired with reward and non-reward during the discrimination learning phase to aid the discrimination. However, particularly problematic for the representation-mediated account just described were the results from Experiment 3 in that report. Initially, rats were taught to discriminate between two auditory and two visual stimuli when only one of the stimuli from each modality was paired with a distinctive outcome (i.e., A1-O1, A2−, V1−, V2-O2). Subsequently, all of the animals were trained on a reversal of this discrimination in which only A2 and V1 were now reinforced. However, one group was reversed such that the same outcome was used within each modality (i.e., A1−, A2-O1, V1-O2, V2−) whereas the other group was trained with different outcomes within each modality during the reversal phase (i.e., A1−, A2-O2, V1-O1, V2−). Rats trained on the latter reversal learned the task more rapidly. Delamater (1998) argued that these results imply that a representation-mediated mechanism of the sort described by Honey and Hall (1989) cannot accommodate these findings because in both reversal tasks the representations of each outcome should be similarly noninformative. Consider a simple reversal involving two auditory stimuli, i.e., A1-US, A2− in phase 1 followed by A1−, A2-US in phase 2. If we admit that during phase 1 A1 evokes a representation of the US then it should continue to do so, at least for some time, during phase 2. In other words, the US representation evoked by A1 will signal nonreinforcement during phase 2 on these trials. As A2 begins to associate with the US during phase 2, however, this will enable A2 to also evoke a representation of the US; but on these trials since reward occurs the US representation will signal reinforcement. Taken together, the US representation will be noninformative because it sometimes signals reinforcement and sometimes nonreinforcement. The point of the Delamater (1998) study was to ensure that in both groups the outcome representations would be similarly noninformative because on some trials they signal reinforcement and on others nonreinforcement. This sort of account, therefore, cannot readily explain why the two groups acquired the reversal at different rates.
As an alternative, Delamater (1998) suggested that when stimuli within a modality are reinforced with distinctive outcomes, then the internal representations of those cues become more distinctive, enabling faster discrimination between them (even if this distinctiveness training occurs over separate phases of the experiment). In contrast, when stimuli from the same modality are paired with the same outcome, then the internal representations of those stimuli will become more equivalent. Gluck and Myers (1993) suggested very similar ideas to these in their neural network model of hippocampal-cortical interactions during learning. Moreover, Honey and his colleagues have produced an impressive amount of additional empirical support for the general claim that stimuli become recoded at some intermediate “hidden” layer of processing (e.g., see Honey, et al, 2010). These ideas, therefore, are quite naturally captured by the neural network approach depicted in Figure 2B.
The manner in which these neural network approaches achieve these effects is not mysterious, and a simple illustration of how this could work is shown in Figure 3. It is assumed that presenting a given stimulus to such a network, activates a set of input units, based on the senory chracteristics of the stimuli, at the lowest level of the network. Since, at the outset of conditioning, the connection strengths between the various input units and the hidden layer units are assumed to be random, then various stimuli presented to the network will randomly activate various hidden layer units in an uncorrelated way. As noted above, the specific pattern of activations of the hidden units can be thought of as the “internal” representation of the stimulus. Over training, however, various connections throughout the network will be modified based on the network’s prediction errors (i.e., differences between the activation values of output layer units and the desired output layer activation values). These modifications will ensure that specific input stimuli will come to activate only specific subsets of hidden units, and that these hidden units, in turn, will be strongly connected to particular outcome units providing that the stimuli activating such hidden units are actually paired with a rewarding outcome on the training trial.
Figure 3.
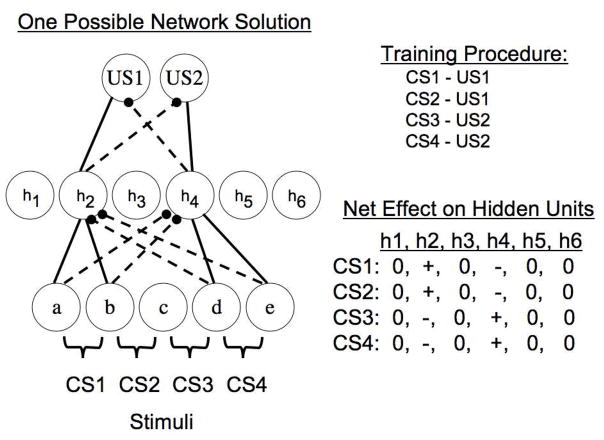
One possible 3-layer connectionist network solution to an acquired equivalence/distinctiveness task. The task consists of four separate training trials indicated to the right. CSs associated with US1 activate h2 but inhibit h4, whereas CSs associated with US2 activate h4 but inhibit h2. The hidden unit h2 develops an excitatory connection with US1 and an inhibitory connection with US2, whereas hidden unit h4 develops the opposite connections with US units. This pattern of connections within the network results in similar hidden unit activation patterns on CS1 and CS2 trials, and also on CS3 and CS4 trials but the two sets of activation patterns are negatively correlated with one another.
In the problem depicted, CS1 and CS2 are each trained with US1 whereas CS3 and CS4 are each trained with US2. Notice that by the end of training the stimulus features activated by CS1 and CS2 form excitatory connections with hidden unit 2 and inhibitory connections with hidden unit 4, whereas the reverse is true for stimulus features activated by CS3 and CS4. Hidden unit 2, in turn, forms an excitatory connection with US1 and an inhibitory connection with US2, whereas the reverse is true for hidden unit 4. Thus, over training, the initially uncorrelated patterns of hidden unit activation by stimuli change such that stimuli predicting the same outcome tend to activate similar subsets of hidden units, i.e., their hidden unit activation vectors become highly correlated. Stimuli predicting different outcomes will, by the end of training, tend to activate subsets of hidden layer units that are negatively correlated with one another. Thus, these basic properties of the network will enable the internal representations of stimuli to become more alike in the case of acquired equivalence treatments and more dissimilar in the case of acquired distinctiveness manipulations (as can be seen by the depiction on the right of the hidden unit activation patterns in the presence of each stimulus).
A New Neural Network Model of Pavlovian Conditioning
The tendencies of neural networks with hidden unit layers to produce converging internal representations in situations where multiple stimuli predict the same outcomes, but diverging internal representations where multiple stimuli predict different outcomes has been noted previously (see Gluck and Myers, 1993; Honey and Ward-Robinson, 2002; Schmajuk and DiCarlo, 1992; Schmajuk, Lamaoreaux, & Holland, 1998). However, what is less clear is whether such networks will accommodate a range of phenomena that would constitute a core set of facts that any model will need to capture. In this section I will introduce a preliminary neural net model that does a reasonably good job of accounting for the acquired equivalence and/or distinctiveness effect described above (Delamater, 1998). Then I will show how the model also captures several other empirical facts concerning various conditional discrimination learning phenomena – facts that any model should be sensitive to. Ways in which this approach might profit from further theoretical development will then be mentioned.
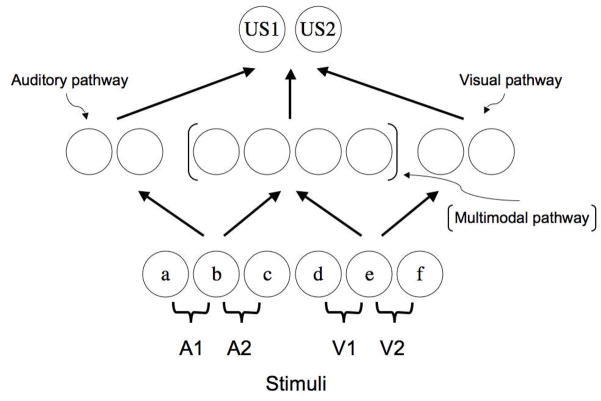
The neural network architecture is presented in Figure 4. This network is similar in spirit to the Schmajuk and DiCarlo (1992; Schmajuk et al., 1998) model in that it assumes that there exist different pathways connecting CS inputs to US outputs. As noted above, I assume that when a given CS is presented to the network it may activate a single input-level unit or some subset of input-level units, depending upon the situation one wishes to model. In other words, at this level one may adopt Blough’s (1975) assumption that different input units are activated according to Gaussian activation functions, or one might more simply attempt to model stimulus similarity, following Rescorla (1976), by assuming that two similar stimuli activate two distinct input units plus a third unit in common. In either case, CSs are assumed to be processed initially by this network by activation of input layer units.
Figure 4.
Connectionist network architecture used in the simulations reported in this paper. Auditory or visual conditioned stimuli (A1, A2, V1, V2) were assumed to activate different sets of stimulus features that could activate US layer units through separate unimodal and multimodal processing pathways. The [ ] symbols indicate that multimodal hidden layer units could be activated by any input stimuli whereas hidden layer units not inside these brackets could only be activated by modality-specific feature stimuli. Arrows indicate the direction of activation as well as places within the network where plasticity (i.e., learning) can take place.
The hidden layer in this model consists of three separate collections of units. Two of these collections are meant to capture the idea that there are stimulus modality-specific pathways connecting physical stimuli to associated outcomes. In this case, one set of inputs, for example, may simulate processing of visual stimuli, while another set of inputs simulates the processing of auditory stimuli. A third collection of hidden units is assumed to reflect the fact that the nervous system is wired in such a way to permit for multimodal processing pathways as well as unimodal pathways (e.g., see Poremba, Saunders, Crane, Cook, Sokoloff, & Mishkin, 2003). This collection of hidden units can receive activation from any input unit, and, thus, captures the fact that there exist in the nervous system structures where auditory and visual inputs converge. Thus, when a visual stimulus is presented it will be permitted to activate hidden units not only from the “visual pathway” set of hidden units but also from the “multimodal pathway” set of units. An auditory stimulus, likewise, will activate “auditory pathway” hidden units as well as multimodal hidden units.
Finally, USs, i.e., reinforcing outcomes, are modeled by distinct units at the output layer. It is at this layer that prediction errors are computed and used to modify connection weights throughout the network.
The model assumes a two-stage process in determining (1) output activation levels, and (2) connection weight adjustments on any simulated conditioning trial. For the simulation results to be presented shortly, I used conventional activation functions and learning rules to govern network performance (see Rumelhart, Hinton, & Williams, 1986). Briefly, input units are activated with a +1 or 0 level of activation (depending upon the CS being present or not). Any given hidden unit activation was calculated by the following formulae:
| (1) |
where ai refers to the activation level of the ith input unit and wih refers to the connection weight (associative strength) between the ith input unit and the hidden unit in question. The net input levels then were converted into an activation value for the hidden unit in question by using a logistic activation function:
| (2) |
Use of this activation function will result in activation levels that range from 0 to 1. However, the normal logistic activation function ensures that an activation level of 0.5 is produced when the net input is 0. Since it is unreasonable to assume that neurons without receiving any input would adopt a resting activation level equal to 50% of their maximal level, the value 2.2 is subtracted from the net input in the exponent in order to shift this activation function to the right such that when the net input is 0 only a very low output activation level is produced (0.1 in this case). This low level of activation in the absence of any input reflects the fact that neurons possess a low spontaneous firing rate.
The process of determining the activation of US units is similar except that these are calculated by summing across hidden unit to US unit connections. Once again, the US unit activation is determined by passing the net input through the logistic activation function. US activation levels calculated in this manner form the basis of the model’s predictions.
Once US unit activations are determined, then the procedures suggested by Rumelhart, Hinton, and Williams (1986) were followed for modifying connection weights throughout the network. The Appendix presents the full set of formulae. Briefly, prediction errors were first calculated by taking the difference between the US unit’s activation level and the desired level for that conditioning trial (i.e., λ). These prediction errors are then used to modify the connection weights between the various hidden units and the US units. In addition, the prediction error is also propagated back through the network to the hidden units in order to determine how to adjust the CS-to-hidden unit weights. Each US unit contains its own prediction error on any given simulated conditioning trial and these, in turn, are passed back to the hidden units as a weighted proportion of their contribution to the total prediction error on the trial. Thus, some hidden units will bear the burden of responsibility more than others for producing the incorrect US predictions and, consequently, connections between input units and these particular hidden units will be more strongly adjusted. This two-step process – activation and weight modification – is followed until the network learns the task, i.e., learns to generate appropriate US-unit activations on every type of conditioning trial presented to the network.
One point worth noting is that this back-propagation learning rule has been criticized for its lack of biological plausibility (e.g., see Schmajuk & DiCarlo, 1992). On the other hand, more biologically realistic learning algorithms (e.g., see O’Reilly, 1996) have been shown to display similar properties to the back-propagation rule suggested by Rumelhart et al. (1986). Thus, as a first approximation towards evaluating the network presented here, this rule was adopted. In future versions of the model the use of different learning algorithms will be explored.
Simulation of the Acquired Equivalence/Distinctiveness Study by Delamater (1998)
In order to simulate the results from Experiment 3 in Delamater (1998) a decision needs to be made concerning how to code the various stimuli used in the experiment. Initially, rats were trained on one visual discrimination and one auditory discrimination but with each reinforced stimulus reinforced with a different US (i.e., V1 – US1, V2 -, A1 −, A2 – US2). These stimuli were modeled in the following way. Each visual stimulus was assumed to activate one distinct input unit together with a second input unit that was activated by both visual stimuli. In other words, inputs A and B were assumed to code the distinct features of the two visual stimuli, respectively, whereas input unit X was assumed to code the common visual features shared by the two visual stimuli. Thus, AX and BX stimuli coded the two visual stimuli. In a similar way CY and DY stimuli coded the two auditory stimuli. Note that X and Y input units are assumed to be units that are activated by all visual or auditory stimuli, respectively. For the purposes of this simulation there were no truly general units in the sense that any stimulus from any modality could activate such inputs. In addition, the two USs used in the study were coded by different output level units.
In simulating this experiment the network was first “trained” with 4 different input-output pairs (corresponding to different conditioning trials: AX – US1, BX-, CY-, DY – US2). Output activations were generated with each input presentation and then prediction errors were generated for each US unit and these were then used to modify connection weights, as described above, throughout the network. The network was trained in this manner eight times, each with a different random configuration of starting weights. Different random configurations of starting weights can lead to different solutions or rates of learning. Conducting multiple simulations, therefore, provides a better estimate of the model’s predictions than simply conducting a single simulation (cf. Schmajuk & DiCarlo, 1992; Schmajuk, et al., 1998). Furthermore, each run can be considered a separate simulated subject in the experiment. Further details can be found in the Appendix.
As can be seen in Figure 5 the model learned to generate appropriate US-unit activations for each of the different simulated conditioning trials. Plotted are the mean activation values for each of the two US units on each of the four trial types across 30-trial blocks during the initial acquisition phase and 20-trial blocks during the reversal phase. These data reflect the average performance across 8 separate simulations (corresponding to different simulated “subjects”). It is clear that by the end of the initial training phase (the first eight blocks of the figure), the network learns to strongly activate the appropriate US unit during AX and DY trials while at the same time keeps US activation levels low on BX and CY trials. In addition, the reinforced AX and DY stimuli selectively activate their associated US units while not activating the other US unit.
Figure 5.
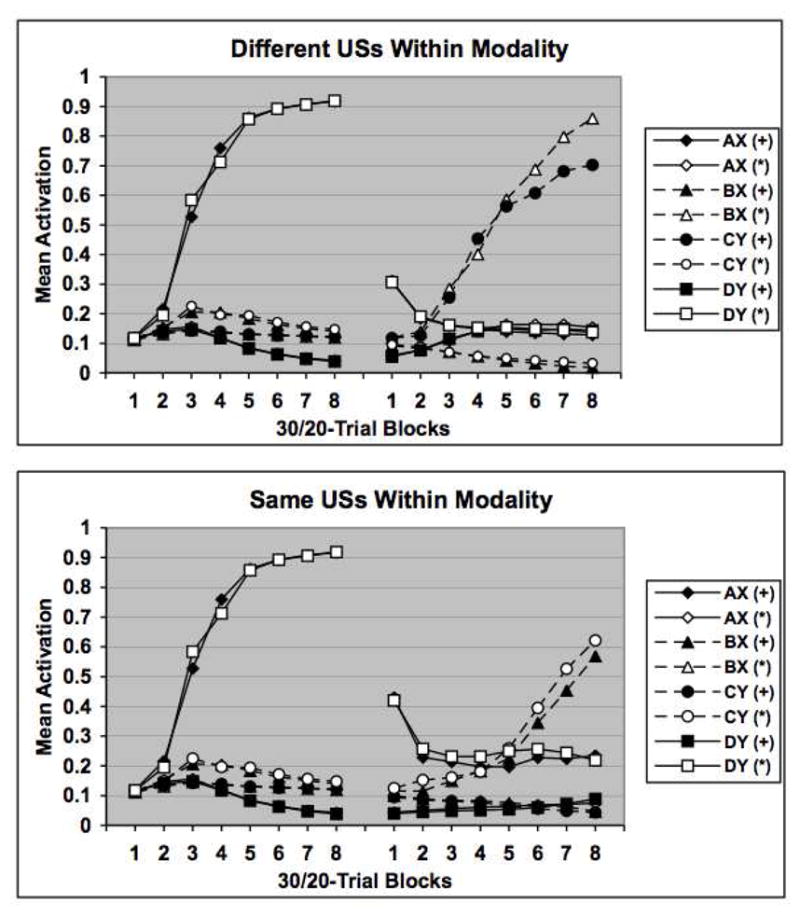
Simulation results of the Delamater (1998) Experiment 3 task. US activation values are presented after separate blocks of training on individual training trials. US1 and US2 activation values are indicated by the symbols + and *, respectively. Individual stimuli are coded by the features they are assumed to activate (AX, BX, CY, DY). The upper graph indicates how the network learns the original discrimination as well as a reversal in which different USs were used within each stimulus modality, whereas the lower graph displays network performance when the same USs were used within each stimulus modality during the reversal phase. Note that activation values are reported for both + and * US representations in the presence of each stimulus. See text for additional details.
Of more interest is how the network performs during the simulated reversal phase. The upper panel of the figure displays the results for the simulated group trained with different USs across phases within each modality (i.e., AX-, BX – US2, CY – US1, DY-), and the lower panel shows corresponding data for the simulated group trained with the same USs across phases within each modality (i.e., AX-, BX – US1, CY – US2, DY-). It is clear that while both groups successfully reverse their US unit activation patterns across the four trial types during the reversal phase, this is accomplished more efficiently in the group trained with different USs within each modality across the two phases. Consistent with the data reported by Delamater (1998) the model successfully simulates that reversal learning should proceed more rapidly in the within-modality differential outcome condition. The model accomplishes this by virtue of the fact that the internal representations across the hidden units tend to converge when the different stimuli from the same modality are reinforced with the same US across the phases. The opposite tendency occurs when different USs are used across the phases, thus, enabling more distinctive internal representations to control performance more efficiently.
Given the success of the model in accounting for the acquired equivalence/distinctiveness effects reported by Delamater (1998), it is reasonable to ask how the model might fare in accounting for a variety of other tasks thought to engage hidden layer representations. As noted above, conditional discrimination tasks are well solved by multilayered network models because hidden layer representations of stimuli permit for solution to so-called non-linear tasks. I have begun exploring the model by asking whether it might capture some of the basic facts about patterning, biconditional discrimination, ambiguous occasion setting, and feature positive and negative occasion setting tasks. In each case, some of the main facts seem to be well reproduced.
Simulation of Patterning Discriminations
Two basic facts about patterning discrimination learning that should be accommodated by any model include (1) that positive patterning discriminations are easier to learn than negative patterning discriminations (e.g., see Bellingham, et al., 1985; Delamater, Sosa, & Katz, 1999; Harris, et al., 2008; Harris, et al., 2009), and (2) the more subtle fact that negative patterning learning is sensitive to the relative salience of the stimuli. In particular, Redhead and Pearce (1995; see also, Delamater, Sosa, & Katz, 1999) discovered that when stimuli with different saliences are used in a negative patterning task, discrimination is first learned between the nonreinforced compound and the less salient element compared to the more salient element. While this basic result presents a challenge to the elemental theory of Rescorla and Wagner (1972) and confirms predictions derived from configural theory (Pearce, 1987; 1994; 2002), it should be recognized that other elemental theories may also anticipate these findings (see also Wagner and Brandon, 2001).
The results of two simulations of patterning tasks are shown in Figure 6. In the first simulation the network was trained with one stimulus from each modality on either a positive (A−, V−, AV+) or negative patterning (A+, V+, AV−) task. In addition, a contextual cue was included on every simulated conditioning trial and also on a separate nonreinforced trial type (simulating the intertrial interval) in which there were no other stimuli present. Including this contextual cue made a difference (to be explained below) in comparing the positive and negative patterning tasks, but the inclusion or not of a context stimulus did not impact any of the other simulation results described in this paper. As before, there were 8 runs through each task and the average performance of the model is shown in the form of US activation levels on the various trial types across blocks of trials. The top panel of Figure 6 shows that the model learns a positive patterning discrimination more rapidly than a negative patterning discrimination. This same pattern of results was also obtained when the contextual cue was not included in the simulation (data not shown). However, in this case, by the end of training performance on the negative patterning task surpassed that of the positive patterning task. This unusual effect can be understood by considering how the network solves these two patterning tasks. In the negative patterning discrimination, the network learns to represent the stimuli on the three different trials differently. In particular, each individual stimulus acquires the capacity to activate the US node through a different route through the hidden layer. On the compound trials the two input stimuli individually come to inhibit one another’s activation of hidden layer units. The result is that three distinct patterns of activation occur at the hidden layer on the three trial types. Only when the two hidden layer activation patterns produced by the two individual stimuli occur will the US unit become fully active. In contrast, in the positive patterning task each input stimulus learns to converge on the same set of hidden units that are strongly connected to the US unit. Responding will naturally be greater on compound trials than on element trials due to a simple (and familiar) summation principle. However, some mechanism must exist to suppress US unit activation on element alone trials. The context acquires this capacity by providing enough inhibition of hidden layer units to suppress the internal representation of each stimulus individually, but not in combination. In this way the relevant hidden layer units function as an “And-Gate.” One interesting prediction stemming from this mechanism is that positive patterning discriminations should be more impaired by a context switch following training than negative patterning discriminations. To my knowledge this idea has not been examined experimentally.
Figure 6.
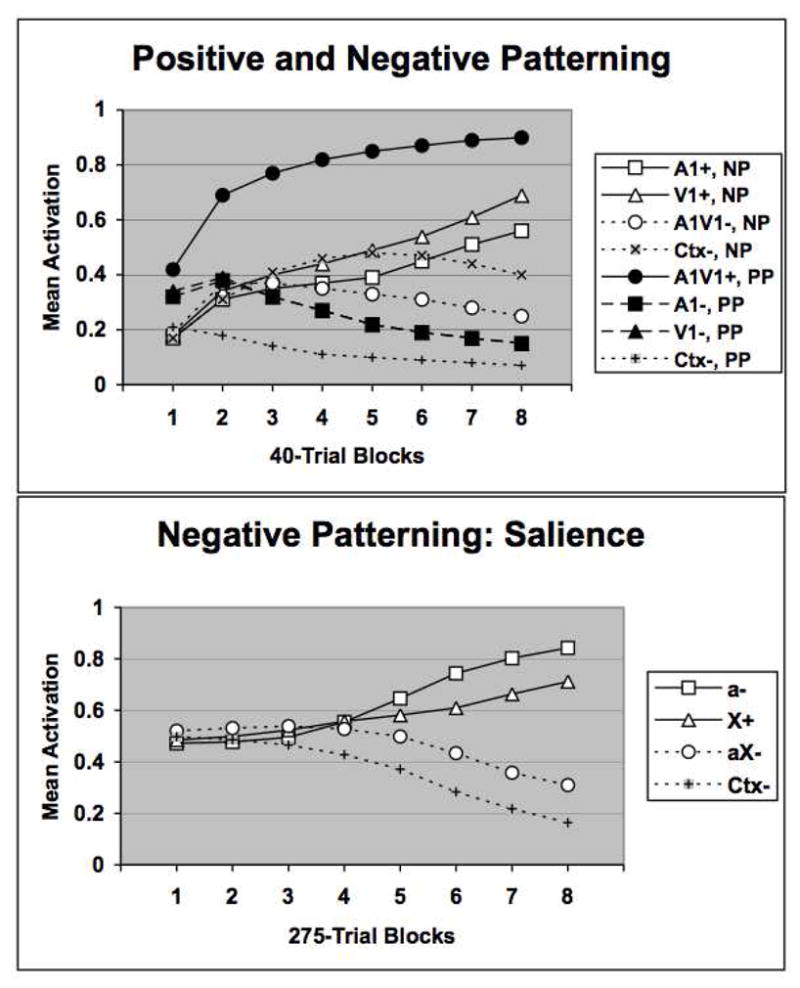
The upper panel compares network performance on negative (NP) and positive (PP) patterning tasks. One auditory and one visual stimulus (A1, V1) were used to train the network on these tasks. In addition a contextual stimulus (Ctx) was also assumed to occur on every trial type as well as when no stimuli were presented. The symbols + and − indicate reinforcement or nonreinforcement, respectively. The lower panel displays network performance on a negative patterning task where the saliences of the two stimuli differed. Stimulus “a” was assumed to be less salient than stimulus “X.”
The bottom panel of Figure 6 shows that the model learns a negative patterning discrimination by more successfully distinguishing the nonreinforced compound from a less salient element compared to a more salient one. This was modeled by assigning a higher input activation value to the salient stimulus, X, compared to the less salient stimulus, a. The results follow from the fact that learning the negative patterning task requires that the model develop three distinct internal representations of the stimuli – one for the more salient element, one for the less salient element, and one for the compound. Since this pattern separation (O’Reilly and Rudy, 2001) process will be more easily accomplished when the stimuli are less similar to one another, as in Pearce’s configural theory, the discrimination between the compound and the less salient element should be easier.
Simulation of a Biconditional Discrimination with Differential Outcomes
Recently, we have demonstrated that rats are able to solve a biconditional discrimination problem more successfully if the reinforced compounds are reinforced with distinct USs (Delamater, Kranjec, & Fein, 2010). We note that a Pavlovian biconditional discrimination is formally equivalent to instrumental biconditional discrimination tasks and given that training with differential outcomes aids learning in the latter situation it may very well aid learning in a Pavlovian task as well. We trained two groups of rats on a task where two long duration visual stimuli (each 2 min in length) were trained with two different short duration (10 s) auditory stimuli occurring in their presence at different times. Only one of the auditory stimuli was reinforced in the presence of one visual “background” stimulus, whereas the other auditory stimulus was reinforced in the presence of the other visual background stimulus. However, one group of rats learned this task with differential outcomes (i.e., V1: A1 – US1, V1: A2−, V2: A1−, V2: A2 – US2), while a second group of rats was trained with nondifferential outcomes (each US occurred with equal probability following each reinforced stimulus). We observed that the group trained with differential outcomes acquired the task more successfully.
This observation can be understood in terms of an acquired distinctiveness effect in subjects given differential outcome training. In other words, discrimination between the two auditory stimuli should be more easily accomplished if each auditory stimulus is reinforced with different outcomes. This would tend to make the internal representations of the two auditory stimuli more distinctive, and this would be a precondition for learning the task. If, by contrast, training with nondifferential outcomes tends to make the internal representations of the two auditory stimuli more equivalent, then, in the extreme where the two auditory stimuli are perceived as the same event, subjects will be unable to solve the task.
Figure 7 shows that the network learns the biconditional discrimination task more readily when differential outcomes are used than when nondifferential outcomes are used. Notice also that the simulated difference is greater than initially appears in the figure because twice as many simulated trials (30- versus 15-trial blocks) were required for the single US task to approach the level of discrimination performance seen in the different USs task. The network solves this problem more rapidly with differential outcomes for the reason specified above, namely, that distinct internal representations of the two auditory stimuli more readily form when the two events are associated with different outcomes.
Figure 7.
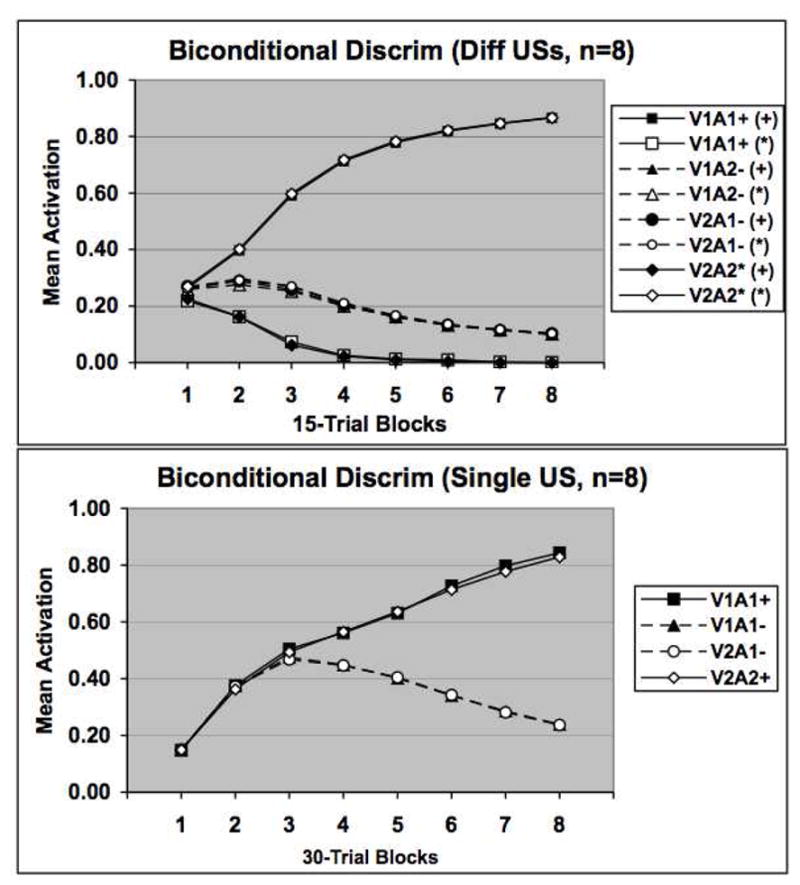
Network performance on a biconditional discrimination task in which different USs (upper) or a single US was used in training. In these tasks the V1A1 and V2A2 stimulus compounds were reinforced whereas the V1A2 and V2A1 stimulus compounds were not reinforced. Symbols are the same as in the previous figures. Note that activation values are reported for both + and * US representations in the presence of each stimulus. See text for additional details.
Simulation of Biconditional and Patterning Discriminations
Harris and his colleagues recently explored the relative speeds that rats performing in a magazine approach paradigm learned positive patterning, negative patterning, and biconditional discriminations (Harris, et al., 2008). They observed that while rats learned a positive patterning discrimination faster than a negative patterning discrimination in a within-subjects task, other rats acquired a biconditional discrimination (with the same stimuli and frequencies of reward and nonreward as in the patterning task) more slowly than either patterning discrimination. In order to simulate these data it was assumed that each of two auditory stimuli activated one common input unit and different distinct input units, and that all three of these input units were processed along the auditory and multimodal stimulus pathways. The same was true for each of two visual stimuli (but the common visual stimulus was different from the common auditory stimulus and each of these visual inputs was processed along the visual and multimodal pathways). The network was then trained with 8 simulated subjects in the patterning task with the following trial types: A1+, V1+, A1V1−, A2−, V2−, A2V2+ (where + indicates reinforcement and – indicates nonreinforcement). The biconditional task was separately trained with 8 additional simulated subjects with A1V1+, A1V2-, A2V1-, A2V2+ trial types. In addition, in order to be consistent with the other simulations reported here a contextual input (capable of activating all hidden units because contexts, by definition, include both auditory and visual components) was present on every trial and also on a trial type in which no other stimuli were present and this latter trial type (simulating the intertrial interval) was nonreinforced.
The results of this simulation, presented in Figure 8, reproduce the main findings of Harris, et al. (2008). In particular, the network acquired the positive patterning task more rapidly than the negative patterning task (as reported above in a “between group” simulation), and also the biconditional task was acquired more slowly than the negative patterning task. The network finds a solution more slowly for the biconditional task than the negative patterning task because the biconditional task is more complex. In this task each stimulus can be construed as simultaneously playing the role of an element both in a negative patterning and a positive patterning task. Therefore, in order for the network to find a solution to this problem four distinct patterns of hidden unit activations must develop for each of the corresponding trial types, but this will be made more difficult because of the more intricate interchangeability of roles for each stimulus in this task relative to the patterning task.
Figure 8.
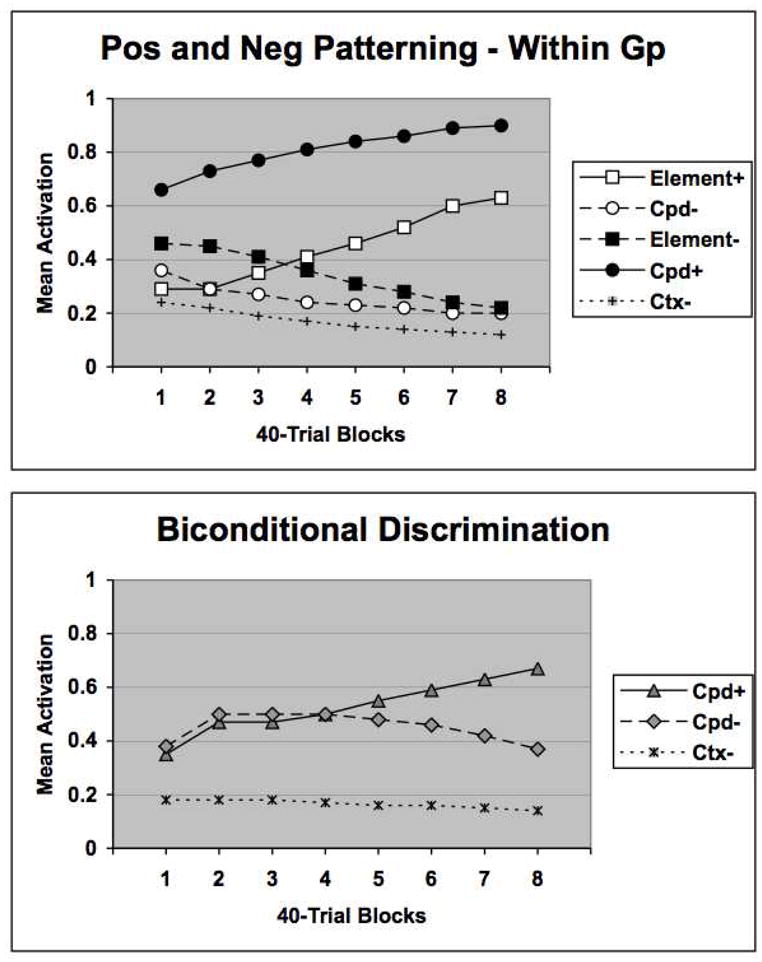
Network performance on the Harris, et al (2008) task. The upper panel compares US activation patterns on element alone and compound trials when the network was trained concurrently with positive and negative patterning problems. The symbols are as in the previous figures. The lower panel displays network performance on a biconditional discrimination task. US activation patterns on reinforced compound (Cpd+) and nonreinforced (Cpd−) compound trials are displayed separately. See text for additional details.
Simulation of Ambiguous Occasion Setting with Differential Outcomes
A closely related discrimination problem to the biconditional task is ambiguous occasion setting. In this task, one target stimulus is reinforced in the presence, but not absence, of a background “occasion setting” stimulus, while a second target stimulus is reinforced only in the absence, but not presence, of the very same background stimulus. Since the background stimulus indicates reinforcement of one target cue but nonreinforcement of a second target cue, its status is, in some ways, “ambiguous.” In the paper mentioned above, Delamater et al., (2010) demonstrated that rats trained in an ambiguous occasion setting task with differential outcomes were more successful in acquiring the task compared to animals trained with nondifferential outcomes. In their procedure one 10-s auditory stimulus was reinforced in the presence of a 2-min visual stimulus, but not in its absence, and a second 10-s auditory stimulus was reinforced in the absence but not the presence of the 2-min visual stimulus. One group of rats was trained with distinct USs occurring with the different auditory cues on reinforced trials, whereas a second group of rats received both types of USs with each auditory cue across reinforced trials. The differential outcome group learned the task rapidly, while the nondifferential outcome group failed to learn the discrimination after 24 sessions of training.
A second aspect of these results is noteworthy and should help to further constrain efforts at modeling these results. The differential outcome group acquired the positive occasion setting component of the task (V: A1 – US1, A1−) more successfully than the negative occasion setting component of the task (V: A2−, A2 – US2). This result replicates other findings of Holland and his colleagues (Holland, 1991; Holland and Reeve, 1991; also Nakajima and Kobayashi, 2000) who reported similar effects (but with a procedure using a single US). Indeed, this basic difference in mastering the different occasion setting components of the task can be a very large difference and, therefore, seems a rather fundamental feature of this form of learning.
Figure 9 displays the results of a simulation of this experiment using the network described above. In the upper panel the results are shown for a simulation of the ambiguous occasion setting procedure when differential USs are used and the bottom panel displays the results when a single US is used. (We have collected other data showing that the rats do not learn any more rapidly when a single US is used compared to when two USs nondifferentially reinforce the appropriate stimuli). Once again, 8 simulated subjects were run in each case and it is clear that the network solves the ambiguous task quite readily, but, importantly, the positive occasion setting component of the task is learned more rapidly than the negative occasion setting component. Further, comparing the upper and lower panels reveals that the network acquires both components of the task more rapidly when different USs are used than when only a single US is used to train the network. This result, once again, is obtained because the network learns to represent the two auditory target CSs more distinctively when they are reinforced with different USs.
Figure 9.
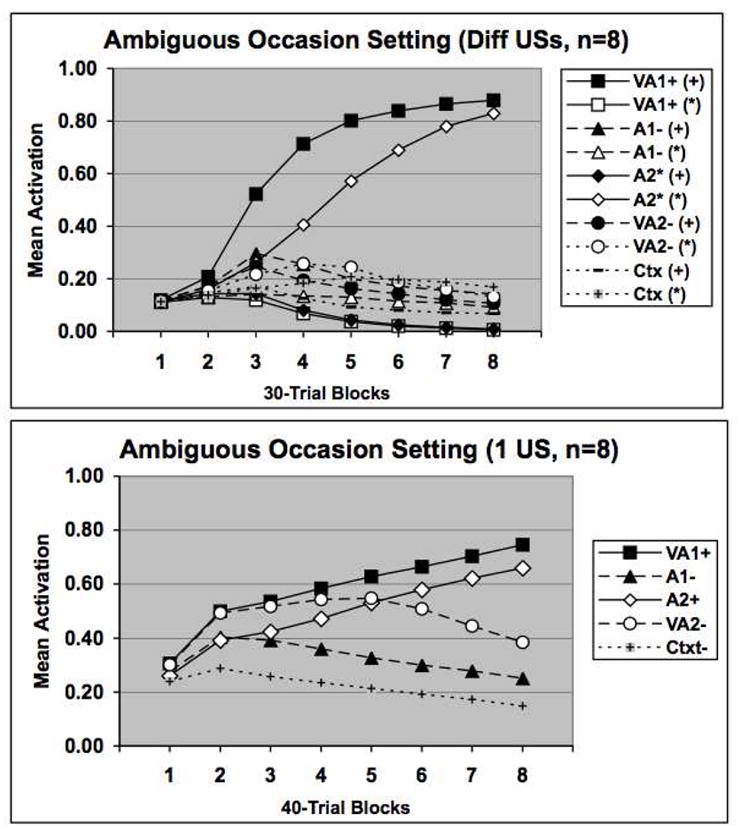
Network performance on the Delamater, Kranjec, & Fein (2010) task. The upper panel displays activation patterns on the separate trials of an ambiguous occasion setting task that used differential USs. The lower panel displays network performance when a single US was used to train the network on the same ambiguous occasion setting task. Symbols are as in the previous figures. See text for additional details.
Simulation of a Feature Positive versus Feature Negative Occasion Setting
A perhaps more fundamental fact about feature discrimination learning is that, quite generally, feature positive discriminations are learned more readily than feature negative discriminations. Not only does this “feature positive” effect occur in ambiguous occasion setting procedures (as noted above), but in more simple feature discrimination tasks as well (e.g., see Hearst, 1984; Jenkins and Sainsbury, 1970). As noted above, it is a rather striking failure of some models that this most basic and robust phenomenon cannot be easily accommodated.
Figure 10 shows the results of a simulation using the neural network introduced here. A within-group comparison between feature positive and feature negative discriminations was simulated. For one of these problems the feature stimulus was assumed to be visual and the target auditory, whereas for the other problem the feature stimulus was auditory and the target visual (i.e., A1V1+, V1−, A2+, V2A2−). The same assumptions for coding similarity within a stimulus modality were made as in the simulations reported above. The results illustrate that the feature positive task is learned more rapidly than the feature negative task, as also occurred in the ambiguous feature discrimination reported earlier. Separate simulations (not shown) also revealed this pattern of results but under conditions where the two feature stimuli were both from one modality and the two target stimuli from the other.
Figure 10.
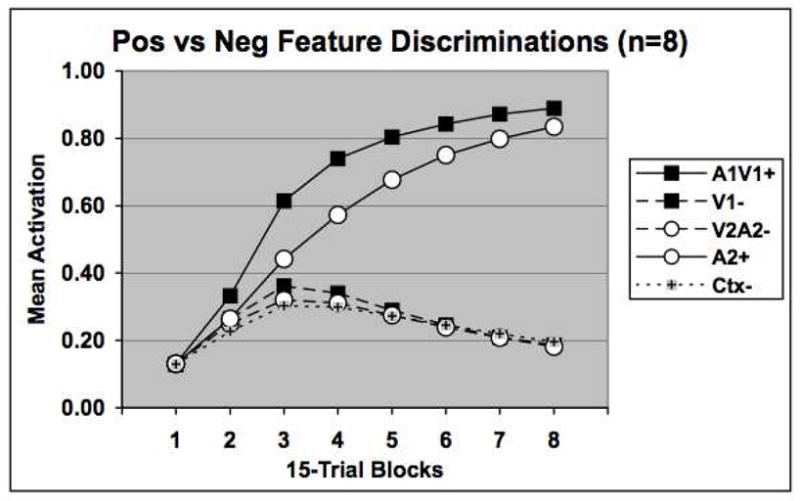
Network performance on a within-subject feature positive (A1V1+, V1−) versus feature negative (A2+, V2A2−) discrimination task.
It is of interest to understand how the network solves these discrimination problems in order to appreciate why the feature positive task is easier to learn. Two mechanisms contribute to this feature positive effect. First, the specific role played by the feature stimulus differs in the two problems. In the feature positive discrimination problem the target stimulus acquires both excitatory and inhibitory connections through the hidden layer to the US unit. The feature stimulus primarily develops excitatory connections through the hidden layer to the US unit. This results in a strong bias of the network to excite the US unit on compound trials but not target alone trials. In contrast, in the feature negative task, the target stimulus develops primarily excitatory connections through the hidden layer with the US unit, while the feature stimulus excites hidden units that inhibit the US unit and also inhibits those hidden units that are excited by the target stimulus. In other words, the feature stimulus becomes both a classic inhibitor of the US as well as an inhibitory modulator (or negative occasion setter) that opposes the target stimulus’ excitatory pathway to the US (see Holland, 1985; Rescorla, 1985). This added complexity in the roles of the feature stimulus in the feature negative task likely contributes to the added time it takes to solve this problem.
The second mechanism that contributes to the feature positive effect has to do with the learning rule itself. The delta rule used in the back-propagation algorithm essentially states that a difference between obtained and predicted outcomes is what governs learning (see also Rescorla & Wagner, 1972). This ensures that early in training when the network fails to strongly activate the US unit positive prediction errors on reinforced trials will be greater in absolute terms than negative prediction errors on nonreinforced trials. Since the size of the prediction error affects the amount, and, hence, rate, of learning, this will lead to faster learning of the feature positive task because, whenever the feature stimulus is presented in this task, the large positive prediction error will ensure that the feature stimulus undergoes a relatively large associative change. The negative prediction error that occurs on feature trials in the feature negative task will be relatively smaller early in training than in the feature positive task, and this will produce a smaller associative change to the feature stimulus.
Some Limitations and Future Developments of the Neural Network Model
The neural network model presented here bears some resemblance to existing models, however there are marked differences as well. For instance, the model is fundamentally elementalistic but configural internal representations may also be learned. Rather than assuming that various configural representations of stimuli are hard-wired into the system (see Wagner and Brandon, 2001) or rapidly recruited on the first presentation of a compound stimulus (Pearce, 1994), the present model allows for elemental or configural solutions to develop as may be determined by the structure of the task. For example, and as also noted by Delamater, Sosa, and Katz (1999; also Bellingham, et al., 1985), a negative patterning task will initially be governed by an elemental process, but with additional training configural processes will control performance as well. This can be clearly seen by the fact that early in training responding to the compound follows the elemental excitatory summation rule, but by the end of training different internal representations of the elements and compound emerge at the hidden layer. This flexible feature of the framework should be regarded as a virtue. It seems unreasonable to assume that the nervous system is hard wired to represent (or instantly recruit a unique representation) of every conceivable configuration of stimuli. This “explosion of representation” problem is easily avoided in the neural network framework by allowing for such unique representations to be learned over the course of training. Thus, this framework offers a more biologically reasonable way to think about configural and elemental representations.
However, and as alluded to above, one major drawback of the present neural network model has to do with the biologically implausible backpropogation rule adopted here. Individual neurons do not appear capable of propogating prediction error signals in the backward direction (e.g., see O’Reilly and Munakata, 2000). On the other hand, it is intriguing that neural circuits for learning do seem to be structured in such a way that implements prediction error computations of the sort envisioned by the Rescorla-Wagner model (e.g., see Cole and McNally, 2007; 2009; Kim, Krupa, & Thompson, 1998). Nevertheless, since the changes in connection weights are assumed to depend upon local computations of error signals, it would be desirable to have a more biologically realistic learning algorithm to implement this. O’Reilly (1996) suggested that a “contrastive” Hebbian rule is more biologically plausible and functions similarly to the backpropagation rule used here. According to this rule changes in associative strength are governed by a comparison between the products of the activations in two units prior to the US being presented versus after the US is presented. Since such a rule only requires comparisons of local activation values, the rule is more biologically plausible (for a more extensive discussion see O’Reilly & Munakata, 2000). It will be important to determine how the adoption of a more realistic learning algorithm will affect performance of the neural network proposed here.
Another important development of the neural network model proposed here will involve extending it to include real time effects. This issue may be intricately intertwined with the appropriate learning algorithm issue because certain learning rules may require recurrent connections within the network (see Honey, et al, 2010), and as soon as recurrence is introduced then it contains real-time elements. This extension will be necessary to help explain real time effects such as the reported differences between sequential and simultaneous feature discrimination tasks (e.g., see Schmajuk, Lamoureaux, & Holland, 1998).
It is of additional interest that the present model offers a framework within which to think of how some stimulus elements might come to “replace” other stimulus elements in their processing (see Wagner and Brandon, 2001; Wagner, 2003; 2008). This interesting idea can perhaps be realized in the present framework by allowing lateral inhibition to occur between hidden layer units. For instance, if multimodal hidden units can exert inhibitory effects on clusters of unimodal hidden units, then this would allow for a natural way of implementing the idea that activation of “context-dependent” configural units can replace “context-independent” units. One major difference, however, is that the present framework assumes no hard-wired competition from the outset. Rather, it allows for plasticity to take this form.
One rather fundamental problem with the neural network model presented here has to do with its account of patterning discriminations. Several aspects are noteworthy. First, Bellingham, et al. (1985) found that rats initially trained on a positive patterning task subsequently learned, only with great difficulty, a negative patterning task with the same stimuli, whereas transferring from a negative to a positive patterning task was not nearly as disruptive. Simulations of this experiment (not shown) revealed that prior training on a negative patterning problem more severely impaired learning the positive patterning task than vice versa. The reasons for this discrepancy are not clear. Second, Pearce and Redhead (1993) demonstrated that a negative patterning problem was learned more slowly when an irrelevant stimulus was added to all the conditioning trials. A simulation of this experiment (not shown) failed to reproduce these results. However, Williams, et al. (2002) also demonstrated that excessively high levels of conditioning accrue to the irrelevant stimulus in this discrimination problem, and this result was also obtained in a simulation of this problem. Third, it was suggested above that negative patterning is learned by virtue of the fact that the network develops different internal representations of the stimuli on each of the three types of conditioning trials. This is accomplished by each stimulus coming to inhibit the other element’s excitatory path to the US. The problem with this solution to negative patterning is that recent evidence suggests that individual elements of a negative patterning task become more functionally equivalent, not distinctive (Grand & Honey, 2008).
More research needs to be performed on this problem because one clear prediction made by the current framework is that training the two elements of the negative patterning discrimination with different USs should enhance the distinctiveness of these cues, and, therefore, enable the network to reach a solution quicker. Given the results of Delamater (1998) it is likely that this effect will be more marked when similar stimuli are chosen. However, if the Grand and Honey (2008) results are general, then exactly the opposite results should be obtained in such an experiment. To my knowledge this has not been empirically explored.
One set of phenomena that seems outside of the present scope is perceptual learning phenomena that serve as the basis for other elemental models (e.g., McLaren and Mackintosh, 2000; 2002). As stated above, the present neural network approach is intended to illustrate how changes in what might be referred to as the perceptual or conceptual representation of stimuli might take place with conditioning. Other effects caused by mere exposure to stimuli in the absence of USs will not be accounted for in the present model. It is perhaps reasonable to think that changes in the manner in which individual low-level stimulus elements might interact with one another (McLaren and Mackintosh, 2000; 2002) or be attended to (Harris, 2006) are best thought of as occurring at the input layer of the present framework. In all likelihood plasticity will occur at many levels within a learning system and a complete model will need to integrate mechanisms from different levels within a more unified approach. Moreover, the present approach suggests that different neural manipulations directed to distinct regions within the processing system should have different effects on these different classes of phenomena (e.g., perceptual learning and acquired distinctiveness phenomena). It remains to be determined whether an investigation of the neural substrates of these two classes of phenomena would support the basic distinction suggested here.
Finally, one further issue is worth some comment. In category learning tasks one common finding is that subjects learn in an initial training phase to sort different sets of exemplars into two distinct categories (i.e., by making distinct responses). Following this training, reversal learning proceeds rapidly when all the members of each category are reversed together compared to when only some of each category are reversed – so-called total reversal shifts are more rapidly learned than partial reversal shifts (e.g., Zentall, et al., 1991; Delamater & Joseph, 2000; Honey & Ward-Robinson, 2001). Neural networks of the sort proposed here will encounter difficulties with this result because connections across the entire network will be altered whenever there are prediction errors, and since there will be prediction errors on every trial in the total reversal condition this will result in a complete restructuring of the network. This is one example of the well-known “catastrophic interference” problem faced by these types of models (e.g., see McCloskey & Cohen, 1989). On the other hand, if the network was to learn to adjust most rapidly the weights of those connections between hidden layer units (the internal representations of the distinct categories) and the output layer units (the category responses) then the total reversal shift advantage will occur. In the total reversal condition this will lead to rapid reversal learning because the exemplar-category mappings that applied in phase 1 also apply in the reversal phase. However, in the partial reversal condition rapid adjustments made from the hidden layer to output layer will result in poor performance because the exemplars are no longer parsed into the same two categories as was learned initially. What would be needed here is a complete remapping of the exemplars to hidden layer category representations. The present framework has no way of accomplishing this in its present form. However, preliminary simulations confirmed that these results occur providing that a parameter is included to allow the network to shift its “attention” from the input layer early in training to the hidden layer representations late in training. This is akin to having the system pay less attention to input stimuli as they become better predictors of its outcomes (Pearce and Hall, 1980) while at the same time increasing attention to hidden layer representations of stimuli (Mackintosh, 1975). While it is becoming increasingly popular to view “hybrid” models of attention (Haselgrove, et al., 2010; Le Pelley, 2004; Pearce and Mackintosh, 2010), the present neural network framework may offer a realistic way in which these different attentional processes may be understood.
In summary, the present neural network model has many ways in which it should be developed to better accommodate existing data. Nevertheless, even in its present form it can handle many of the basic facts of discrimination learning that any theory should be able to address. The present model differs from most in emphasizing changes in the perceptual representations of stimuli. By emphasizing such changes it offers us a natural way of conceptualizing acquired distinctiveness/equivalence effects together with a wide variety of conditional discrimination learning effects.
Nature of the US
Returning now to the standard model of Pavlovian learning depicted in Figure 1, the other main topic to discuss here concerns the nature of the US representation. Historically, theorists have treated this issue quite independently of specifying the nature of the CS representation. A considerable amount of research concerning the issue of “what are the determinants of learning?” led to discussion of how organisms process stimuli in compound conditioning situations. This, in turn, led to the development of a plethora of basic learning models, such as those noted above, that were all concerned with specifying how organisms learned about particular stimuli present in given situations. However, a second key issue in the study of basic learning processes has been concerned with the question of “what is learned?” For an analysis of Pavlovian learning, this issue is directed more to the question of specifying the nature of the US representation. While, ultimately, I believe that these two main issues are intimately interrelated, current levels of understanding do not permit for an adequate integration. Whereas our level of understanding of how CS representations operate during learning is fairly advanced, the amount of basic empirical research directed to the nature of US representations, and, as a result, the level of theoretical sophistication in this realm is more limited by comparison. Nevertheless, a rather intriguing story concerning the nature of the US representation in Pavlovian learning is currently emerging. The point of this section of the paper will be to explore several of the key elements of learning and also attempt to identify some critically important questions that will require further analysis. This part of the review will take on a different flavor, but it is hoped that by discussing this work here it will serve to further encourage the development of a more integrative framework that acknowledges key problems in the study of both CS and US representations.
It is commonly recognized in the literature that unconditioned stimuli are complex events consisting of a variety of attributes (e.g., see Konorski, 1967; Wagner and Brandon, 1989). When a CS comes to associate with a US it can potentially enter into associations with each and every one of these US attributes (see also Delamater and Oakeshott, 2007). For example, the US is a specific sensory event characterized by a number of particular sensory and perceptual features. It is also an event that elicits an immediate and presumably short-lived hedonic reaction (of positive or negative valence), as well as a more generalized and presumably longer-lived motivational/emotional state (appetitive or aversive). Evidence to support this distinction comes from studies showing that “liking” and “wanting” processes involve different neural substrates (e.g., Berridge, 2009; Smith, Berridge, & Aldridge, 2011). The US is also a biologically significant event that occurs at a specific point in time. And, finally, it is an event that is itself capable of evoking specific responses or sets of responses. All of these attributes may, indeed, prominently figure into the learning that occurs when a given CS comes to associate with a given US.
There are clear examples in the literature illustrating that a CS associates with some, but not all, of these various US attributes. In this section I will selectively review some of the many studies supporting at least some of these claims and also point out areas in need of further exploration. In addition, a supplementary question arises from this perspective, and that has to do with the issue of the independence of learning about these different US attributes. This question has not been thoroughly studied although there is relevant evidence concerning potential distinctions in learning about different US attributes. Some of this work will also be described in this section, though this work is really only in its beginning stages.
Learning about specific sensory features of the US: Images and expectancies
There are a wide variety of studies illustrating that in Pavlovian conditioning the CS enters into an association with some of the highly specific sensory qualities of the US. This claim receives support from studies examining US devaluation effects (e.g., Colwill and Motzkin, 1994; Holland and Rescorla, 1975; and for an early review see Delamater and LoLordo, 1991), US-specific reinstatement effects (Delamater, 1997), US-specific contingency effects (Delamater, 1995; Ostlund and Balleine, 2007, 2008), US-specific Pavlovian-to-instrumental transfer effects (e.g., Kruse, et al., 1983), US-based acquired distinctiveness of cue effects (Delamater, 1998; Delamater, Kranjec, and Fein, 2010), US-specific excitatory summation effects (Rescorla, 1999; Watt & Honey, 1997), and mediated conditioning and extinction effects (e.g., Holland, 1990). However, although there is good evidence to support the basic claim that CSs associate with specific sensory qualities of USs, it is less clear just what is the nature of the sensory-specific quality of the US then enters into this association.
One intriguing possibility is that there may be two quite distinct sensory-specific components of reward that enters into the learning. One of these could be a rather low-level sensory “image” of the US (see also Hall, 1996) (much like what occurs when the US is actually presented), while the other might be a more high-level “expectancy” of the US (as occurs when one anticipates an event without actually experiencing it). Consider the following set of studies.
Delamater, LoLordo, and Berridge (1986) studied the orofacial taste reactivity responses rats displayed to plain water under conditions when water was presented alone, when water was accompanied by an auditory CS that had previously been paired with sucrose, and when water was accompanied by a different auditory CS that had previously been paired with quinine. It was observed in this study that rats displayed orofacial taste reactivity responses to water in a manner that was appropriate to the taste predicted by the auditory cue. It is tempting to conclude from this study that the auditory cue for sucrose caused the rats to perceive water as though it actually was sucrose, and the auditory cue for quinine caused the rats to perceive water as though it was quinine. This result alone, however, does not uniquely support this conclusion because the specific responses that the auditory cues elicited in response to water also had an opportunity to directly associate with the cues during the earlier training phase when sucrose and quinine, respectively, were paired with those cues.
However, this interpretation cannot be applied to a set of findings reported more recently by Holland and his colleagues. Kerfoot, Agarwall, Lee, and Holland (2007) used the same general procedure as Delamater et al (1986) but, prior to assessing the effects of the auditory CS associated with sucrose upon taste reactivity responses to water, sucrose was first devalued through pairings with LiCl in some subjects. These authors observed (like Delamater, et al, 1986) that the sucrose-paired CS caused non-devalued control rats to display highly ingestive taste reactivity responses characteristic of those seen to sucrose itself, but, more importantly, the CS caused sucrose-devalued rats to display highly aversive taste reactivity responses to water. This result more strongly suggests that the CS evoked a highly specific representation of sucrose at the time water was being consumed, and this was responsible for determining the taste reactivity responses shown to water.
It still remains to be determined if this sensory-specific representation of sucrose is best characterized as an “image” of sucrose or an “expectancy.” Additional findings are relevant to this question. Holland, Lasseter, and Agarwal (2008) recently extended an earlier finding of Holland (1998) in which it was demonstrated that mediated conditioning but not US devaluation effects are affected by the amount of CS-US training trials administered prior to the critical treatment. For instance, Holland, et al (2008) demonstrated that the influence of an auditory cue for sucrose upon the rats’ taste reactivity responses to plain water is diminished as the number of CS-US pairings is increased. However, at the same time, these authors also reported that the number of training trials did not reduce the sensitivity of the auditory-cue-evoked magazine approach response to sucrose devaluation. In other words, following a large number of conditioning trials the auditory cue was capable of evoking a sensory-specific representation of sucrose that could diminish magazine approach responses when sucrose was devalued, but the cue would not simultaneously cause the rats to misperceive water as though it actually was sucrose. The cue seems to be having at least two effects in these circumstances. With minimal amounts of training, the cue causes the rat to actually perceive (hallucinate) water as though it was sucrose, but with extended training the rat seems to realize that in the presence of the CS although the water is not sweet, sucrose is still likely to be delivered to the food well. In this sense, it appears as though the CS initially evokes a specific “image” of sucrose, but with extended training the CS loses this ability but maintains the ability to evoke an “expectation” that sucrose will occur. Both representations are sensory-specific, but they have different functional properties.
The story is made more interesting by additional recent observations that a cue for sucrose and sucrose itself have been shown to activate overlapping populations of neurons within the gustatory cortex (GC) and also the basolateral amygdala (BLA). In these studies Saddoris, Holland, & Gallagher (2009) and Desgranges, et al (2010) used immediate early gene staining techniques to demonstrate that an olfactory-gustatory cue paired with sucrose activated some of the very same cells within the GC or BLA that were also activated by sucrose presented alone. Furthermore, many more of these doubly activated cells were observed under conditions where the CS and US were paired during training than when they were unpaired, suggesting that this effect was due to conditioning. These data provide direct confirmation of the idea that a CS comes to at least partly activate a psychological process that is also activated by the US itself. Further work will be needed to clarify exactly the nature of these overlapping cell populations when CSs and USs are presented, but the results are highly suggestive of the possibility that the CS evokes an image of the US (at least early in training).
Learning about general motivational features of the US
There is ample evidence to suggest that when a CS and US are paired the CS enters into an association with some rather general central motivational state, and that this association is quite different from that formed between the CS and the sensory properties of the US (as discussed above). Following Konorski (1967), Wagner and Brandon’s (1989) AESOP theory makes this assumption explicit. Some compelling evidence comes from transreinforcer blocking studies in the 1970s and, more recently, from Pavlovian to instrumental transfer studies.
One particularly interesting demonstration was provided by Dickinson and Dearing (1979). In this study, one stimulus was trained with a Pavlovian conditioned inhibition procedure as a signal for the absence of food reward. This stimulus was then presented with a second stimulus and the compound was paired with a shock US. Aversive conditioning to the second stimulus was then assessed in separate test trials, and it was observed that prior conditioning of the first stimulus as a conditioned inhibitor for food enabled this cue to successfully block aversive conditioning to the added cue during aversive conditioning. The most natural interpretation of this result is that appetitive inhibitory conditioning resulted in the first stimulus acquiring an association between the cue and some central aversive motivational state. If during fear conditioning a cue would normally associate with this same (or similar) aversive motivational state, then blocking by an appetitive inhibitory stimulus could very well take place. If one did not appeal to this mechanism it is difficult to understand this pattern of results. It is also worth noting, however, that the basic ideas that this logic is based on have not received much attention in the years since this report appeared.
Another approach to this issue comes from more recent studies of Pavlovian-to-instrumental transfer and its neural basis. Blundell, Hall, and Killcross (2001; also Corbit and Balleine, 2005) trained hungry rats to press one lever for food pellets and another lever for liquid sucrose. In separate training sessions conducted off-baseline, two different Pavlovian cues were separately paired either with the food pellet or sucrose US, respectively. In a subsequent transfer test, each CS was presented in test sessions where both instrumental responses were concurrently available. Control subjects displayed above-baseline levels of responding in the presence of both CSs, and, in addition, a greater elevation of the response previously reinforced with the same US as that associated with the test CS. These results suggest that the CS’s evoked both a generally activating central motivational state as well as sensory-specific representations of their associated USs. These processes, respectively, were responsible for general and selective Pavlovian to instrumental transfer. In contrast, a second group of animals was trained and tested in the same manner, but these animals had been given pre-training lesions of the BLA. In these subjects, both CSs increased instrumental responding above pre-stimulus baseline levels, however, the selective transfer effect was lost. This result suggests that while these animals were incapable of forming associations with the sensory-specific properties of reward, the stimuli, nevertheless, did form associations with the general motivational properties shared by the two appetitive rewards. Increased instrumental responding in the presence of these cues presumably reflects the increased general activating effects of such a state upon performance (see also Rescorla and Solomon, 1972).
Learning about temporal features of the US
There are a wide variety of ways of illustrating that during Pavlovian conditioning animals learn about the temporal location of the US. Indeed, various theories of Pavlovian learning are built on the very premise that timing processes play a significant role in learning (e.g., Balsam & Gallistel, 2009; Arcediano & Miller, 2002; Gallistel & Gibbon, 2000; Gibbon & Balsam, 1981). When a CS, for instance, comes to evoke a CR just prior to the US, then how can this learning be best characterized? An answer to this question goes beyond the scope of the present article, but for the present it is worth stating the basic problem. On the one hand we can assert that associations between events are learned whereby some representation of time is incorporated into that association (e.g., Cole, Barnet, & Miller, 1995). What exactly this means is not obvious, but if we had a good understanding of how the brain represents specific temporal intervals (e.g., see Church & Broadbent, 1990), then it seems possible that stimuli could come to associate with such representations and provide a basis for an explanation. On the other hand, some have advocated abandoning, altogether, the associative framework in favor of a more computational approach where temporal intervals are at the core of what is learned (e.g., see Balsam & Gallistel, 2009). Clearly, some consensus on this issue will require a clearer integration between theories of timing and of associative learning than is presently the case.
Learning about hedonic characteristics of the US
It is also logically possible that when CS and US are associated, the CS may form a direct connection with the hedonic qualities of the US. This possibility may be especially likely in flavor preference paradigms where flavor cues are mixed in solution with highly palatable nutrient USs. Harris, Shand, Carroll, and Westbrook (2004) suggested that this possibility might contribute to observations of why conditioned flavor preferences persist following extinction manipulations. However, Dwyer, et al. (2009) more recently provided evidence to suggest that a learned flavor preference persists even after conditioned hedonic responses shown to the flavor cue extinguish, as assessed with a detailed analysis of licking patterns. Thus, an appeal to hedonic associations to explain persisting learned preferences following extinction may not be warranted.
Nevertheless, the general question is a valuable one to ask and there is, unfortunately, very little evidence in the literature that can provide an adequate answer at the present time. Perhaps what is needed is some way to isolate associations based on hedonic and sensory properties of reward and differentially manipulate those associations experimentally. For instance, it has already been mentioned above that the BLA may be critically involved in the encoding of sensory-specific CS-US associations. Other structures (e.g., the orbitofrontal cortex) may also play critical roles (see Delamater, 2007b). If damage to one of these regions could be shown to eliminate control by sensory-specific associations while at the same time not impair control by hedonic associations, then this would be promising. The problem is that it is not so clear what would constitute a good measure of control by hedonic associations. Perhaps some measure of palatability (e.g., orofacial taste reactivity or lick patterns, see Dwyer, 2008; Dwyer, et al., 2009) could be useful in connection with lesion techniques to provide more direction on this problem.
Learning about specific responses to the US
This final category of learning is perhaps the most difficult one to assess. Authors have sometimes assumed that after a conditioned response has been established what remains of that response following a US devaluation treatment must be understood in terms of S-R associations. However, as Colwill and Rescorla (1990) demonstrated some time ago even under conditions where residual conditioned responses remain following a US devaluation treatment, a more complete US devaluation treatment more successfully abolishes conditioned responding. Thus, we will not know if residual responding reflects residual US value or control by some associative structure that is unaffected by the US devaluation technique.
Another logical problem is that if residual responding occurs despite complete loss of US value in a devaluation test, we would not know whether this reflects control by S-R associations or some other associative structure that is also insensitive to US devaluation (such as associations with the hedonic properties of the US or with the general motivational properties of the US). The problem with inferring S-R associations as a default is that there are too many other default possibilities. Until we can assess more directly the presence of S-R associations, it will likely be impossible to provide evidence for them. Once again, evidence at the neural systems level of analysis may be a more promising route to take in this regard. If plasticity can be shown to take place directly between a sensory and motor neuron, then this would be clear evidence to support the S-R possibility. However, in organisms more complex than the simplest, evidence of this sort will likely be harder to come by.
On the possibility of independence of learning
If we admit that the US is a complex event, including multiple component features (sensory, hedonic, motivational/emotive, temporal, response) then one very natural question concerns whether learning about these multiple components of the US occurs independently or in an interdependent manner. There is not much data examining this issue, but it is an important one. Current work at the neural systems level of analysis is beginning to provide some evidence that is relevant to the question.
In one study, Corbit and Balleine (2005) demonstrated that learning about the sensory-specific and general motivational qualities of food reward rely on different underlying neural substrates. These authors used a variant of the Pavlovian-instrumental transfer design described above to show that stimuli can exert outcome-specific and outcome-general control over instrumental responses, and that each of these forms of transfer depends upon different neural substrates. In particular, they demonstrated that animals given pretraining BLA lesions displayed no selective Pavlovian-to-instrumental transfer, but they did display general transfer, and that, conversely, other animals given pretraining lesions of the central nucleus of the amygdala displayed selective but not general transfer. The results imply that learning about the sensory specific and general qualities of reward can occur independently of one another (see also Betts, Brandon, and Wagner, 1996).
This evidence is compelling. However, it raises another question. If the two forms of learning can be acquired independently of one another in brain-lesioned animals, do they interact in any way under normal circumstances? To address this issue Gewirtz, Brandon, and Wagner (1998) examined the effect of long duration “contextual” cues on eyeblink conditioning in rabbits. These authors found that a contextual cue blocked or facilitated learning of an eyeblink CR when a short duration CS was paired with an eyeshock US in its presence. If the locus of the shock US during the pretraining and blocking phases was the same then blocking was observed. However, if the locus of the shock US was to different eyes in the two phases, then the contextual cue facilitated learning to the CS. This result was interpreted as reflecting the possibility that in the latter condition, facilitated learning occurred because the general aversive motivational state evoked by the contextual cue heightened processing of the CS, and this enabled it to be more strongly associated with the US. This effect would have been counteracted by a blocking effect when the locus of shock was the same in the two phases. Thus, there is some evidence to suggest that, as Konorski (1967) had earlier speculated, learning about motivational properties of reward may positively influence learning about other properties of reward.
These two strands of evidence are interesting, but the story is far from complete. For one thing, very different learning paradigms were used in the two studies noted above, so the generality of the results is unknown. Furthermore, if sensory-specific and general motivational learning processes are distinct but interacting processes, other questions present themselves. For instance, what is the nature of the learning rules that govern learning within a given system? Can we assume, for instance, that whatever learning rule we wish to adopt, that the same rule applies to learning of each and every type of association mentioned above? It is probably unwise to make such an assumption. Thus, the door is wide open to examining the possibility that the variety of types of associations mentioned here may obey different learning rules in different learning systems.
Once again, there is some intriguing neural systems work on this possibility. Delamater (1995) demonstrated that when CSs are paired with distinct USs but one of those USs is also presented noncontingently during the intertrial interval, conditioned responding selectively decreases to the CS whose contingency has been degraded. More recently, Ostlund and Balleine (2007; 2008) demonstrated that post-training lesions of the orbitofrontal cortex (OFC), the mediodorsal thalamus (MD), and the BLA had different effects upon sensitivity to this selective contingency degradation procedure. In particular, in all three cases rats lost the selectivity of the contingency degradation. However, with OFC and MD lesions the rats decreased their response levels to both CSs equally. It was as though these subjects encoded both USs in the same way, and so their learning was based on a general contingency degradation process. However, BLA lesioned-rats maintained their response levels at high levels as though these subjects were insensitive to the contingency-degradation process itself. The authors suggested that these rats no longer were sensitive to the selective prediction error process that supports contingency learning, and, instead, were maintained through purely contiguity mechanisms.
This intriguing possibility would point to the presence in the nervous system of both contiguity and prediction error mechanisms, and also lead to the suggestion that multiple learning rules might apply in different circumstances. The interesting theoretical question then emerges as to the nature of the learning rules for the various types of learned associations reviewed in this section. Further research will hopefully provide some answers.
The same sort of interaction question can be applied to learning of the different types of associations discussed above. One particularly interesting contrast is between learning about sensory and temporal properties of reward. Delamater and Oakeshott (2007) presented some evidence to suggest that these two forms of learning might involve different systems (see also Delamater & Holland, 2008), but firm conclusions regarding the nature of these systems and their interactions will require further work.
Closing Thoughts on the Nature of CS and US Represenations in Pavlovian Learning
At the very heart of a modern analysis of Pavlovian learning is the idea that learning consists of the formation of new connections between mental representations of CS and US – what has been referred to as the standard model. The main thrust of the present paper is that while this general statement can be taken as reasonably accurate, at the same time the overall approach becomes much more rich with additional questions when one considers in more detail the nature of the mental representations of CS and US.
I have offered one way of developing the idea that CS representations might change over the course of learning, and how such changes can be thought about while still maintaining an associative approach. While some of the details of the connectionist model proposed here will most surely require modification, I hope I have persuaded the reader that the key ideas have merit. In particular, since sensory systems are organized with separate modality-specific and multi-modal processing streams, it seems reasonable to constrain a connectionist model to include these separate processing streams. In addition, I have emphasized the importance of incorporating into the network architecture a hidden layer of processing elements. Given the complexity of the brain it seems that our standard model in which connections form directly between CS and US representations will, in the end, be considered an oversimplification, as we have always imagined it to be. Perhaps now is the time to take more seriously the idea that more complexity is, indeed, advantageous in theory development (see also, Gluck and Myers, 1993; Honey, et al., 2010; Schmajuk, Lamoureaux, & Holland, 2008). The incorporation of a hidden layer into the formulation of learning has the advantage, as noted above, of providing us with a way of conceptualizing how the representation of the CS might evolve over the conditioning experience. At a psychological level, this can be thought of as one way in which sensation and perception differs. There might be inherent truth to earlier ideas that perception involves both refinement as well as embellishment (see Gibson & Gibson, 1955). Perhaps the sort of learning to refine sensory experiences, rendering them more veridical with the physical source of stimulation, is what occurs at a low level within the processing system, but the more elaborative process is what takes place at deeper levels of processing – here captured by the hidden layer. In any case, the inclusion of the hidden layer increases the breadth of phenomena that can be fairly plausibly explained. In particular, I have shown how a variety of phenomena from conditional learning to patterning and acquired equivalence-type tasks can be brought under the same umbrella.
The other main part of this paper was to discuss the question concerning the nature of the US representation. At least since Konorski (1967) we have seriously entertained the idea that Pavlovian learning entails the association of the CS with sensory and motivational/emotive elements of the US. But this, it seems, is only the start. The US has hedonic, response, and temporal qualities as well, and learning involving these other features very likely also takes place, although the evidence is not overwhelming at present. Furthermore, I have reviewed data above suggesting that the CS associates with different types of specific sensory US representations – images and expectancies. The results that this claim is based on are very intriguing and highlights further the idea that important changes take place across conditioning.
The specific way in which the brain processes USs is undoubtedly complex. The task for the theorist is multi-fold. First, we must understand which categories of US features enter into learning. I have reviewed, very selectively, studies indicating that sensory, motivational, and temporal aspects of the US are well learned about. However, other questions remain concerning hedonic and specific response properties of the US. Second, we must understand the degree to which learning about different US features involves independent or interdependent systems. This issue is only just beginning to receive attention. Current research suggests that learning involving sensory and motivational qualities of reward depend upon separate underlying systems, but that they may interact as well. Large looming questions remain, however, in terms of the independence of other learning systems, particularly involving temporal features of reward and its interaction with sensory and/or motivational qualities. Balsam and Gallistel (2009; Balsam, Drew, & Yang, 2002) have recently put forth the radical claim that learning is first and foremost about temporal intervals and temporal uncertainty reduction. Associative learning is entirely secondary to this other temporal learning system. It remains to be seen how far this idea will lead us, but it will surely be important for us to determine to what extent interactions take place between various learning systems. For instance, ‘to what extent do different systems involve different learning rules?’ and ‘how do such systems interact?’ are just some important questions that we will need to cope with in order to press the analysis further.
Finally, I have spoken about the nature of CS and US representations as though these were separate questions. The connectionist network model proposed here regarded the US representation in terms of its sensory specific features. Ultimately, however, we will need to integrate our understanding about both CS and US representations in the context of some more comprehensive modeling efforts. Just what form this will take will very likely depend upon answers we provide about some of the interaction questions raised above. Wagner and Brandon’s AESOP theory (1989) represents one such attempt along these lines. Recent work distinguishing between images and expectancies shows this to be an oversimplification. In addition, if learning systems are truly independent, in the sense that they obey different learning rules, then these requirements will need careful consideration.
All in all, there is much to be excited about in associative learning theory. There is increasing sophistication with which problems are studied, there is much effort directed to the analysis of the neural systems of learning, and there are many interesting empirical and theoretical problems that will need further analysis. I have tried to illustrate one perspective that may be useful in helping us approach some of these pursuits for the next several years. I suppose time will tell if this is a useful one.
Acknowledgments
Some of the research cited here was supported by National Institute of Mental Health (065947) and Professional Staff Congress – City University of New York (62413-00 40) grants awarded to the author. The author gratefully acknowledges Stefano Ghirlanda for stimulating discussions concerning the neural net model presented here.
Appendix
The equations used in the simulations reported here were based on those found in Rumelhart, Hinton, & Williams (1986). The activation functions used throughout the network are presented in the text as equations (1) and (2). Presented here are the equations used for determining prediction error terms for US units and for hidden units. In addition, the equation used to modify connection weights throughout the network is also presented.
Prediction Errors of US units
The following equation was used to calculate US unit prediction errors:
| (1) |
where δi is the US unit’s prediction error, λ is the target US activation level (1 for reinforcement and 0 for nonreinforcement) and ai is the current activation level of US unit i. The product of the second and third terms, ai (1 − ai), is the derivative of the activation function and this is needed in order to guarantee that the network undergoes smooth gradient descent in prediction error reductions.
Prediction Errors of hidden units
| (2) |
where δi is the prediction error for hidden unit i, ai is the current activation level of hidden unit i, δj is the prediction error (as defined above) for US unit j, and wij is the associative strength between hidden unit i and US unit j. Notice that the “prediction error” for a given hidden unit is calculated by summing across the US prediction error terms for each US unit weighted by the strength of the connection between the hidden unit in question with those US units. This is then multiplied by the derivative of the hidden unit activation function in order to ensure proper gradient descent.
Learning Rule
| (3) |
where Δwij(t) describes the weight change on trial t, α is a learning rate parameter (assumed to be 0.1), ai is the activation level of the sending unit, δj is the error term for the receiving unit, and β is a “momentum” parameter (assumed to be 0.9) that ensures smooth and rapid gradient descent. Notice that with this momentum parameter changes in connection strengths on trial t are a function of the change in strength that took place on trial t-1.
References
- Arcediano F, Miller RR. Some constraints for models of timing: A temporal coding hypothesis perspective. Learning and Motivation. 2002;33 (1):105–123. [Google Scholar]
- Balsam PD, Gallistel CR. Temporal maps and informativeness in associative learning. Trends in NeurosciencesR. 2009;32(2):73–78. doi: 10.1016/j.tins.2008.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balsam PD, Drew MR, Yang C. Timing at the start of associative learning. Learning and Motivation. 2002;33:141–155. [Google Scholar]
- Bellingham WP, Gillette-Bellingham, Kehoe EJ. Summation and configuration in patterning schedules with the rat and rabbit. Animal Learning & Behavior. 1985;13:152–164. [Google Scholar]
- Berridge KC. ‘Liking’ and ‘wanting’ food rewards: Brain substrates and roles in eating disorders. Physiology & Behavior. 2009;97:537–550. doi: 10.1016/j.physbeh.2009.02.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betts SL, Brandon SE, Wagner AR. Dissociation of the blocking of conditioned eyeblink and conditioned fear following a shift in US locus. Animal Learning & Behavior. 1996;24(4):459–470. [Google Scholar]
- Blough DS. Steady state data and a quantitative model of operant generalization and discrimination. Journal of Experimental Psychology: Animal Behavior Processes. 1975;1:3–21. [Google Scholar]
- Blundell P, Hall G, Killcross S. Lesions of the Basolateral Amygdala Disrupt Selective Aspects of Reinforcer Representation in Rats. The Journal of Neuroscience. 2001;21:9018–9026. doi: 10.1523/JNEUROSCI.21-22-09018.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church RM, Broadbent HA. Alternative representations of time, number, and rate. Cognition. 1990;37:55–81. doi: 10.1016/0010-0277(90)90018-f. [DOI] [PubMed] [Google Scholar]
- Cole RP, Barnet RC, Miller RR. Temporal encoding in trace conditioning. Animal Learning & Behavior. 1995;23:144–153. [Google Scholar]
- Cole S, McNally GP. Opioid receptors mediate direct predictive fear learning: evidence from one-trial blocking. Learn Mem. 2007;14(4):229–235. doi: 10.1101/lm.489507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole S, McNally GP. Complementary roles for amygdala and periaqueductal gray in temporal-difference fear learning. Learn Mem. 2009;16(1):1–7. doi: 10.1101/lm.1120509. [DOI] [PubMed] [Google Scholar]
- Colwill RM, Motzkin DK. Encoding of the unconditioned stimulus in Pavlovian conditioning. Animal Learning & Behavior. 1994;22:384–394. [Google Scholar]
- Colwill RM, Rescorla RA. Effect of reinforcer devaluation on discriminative control of instrumental behavior. Journal of Experimental Psychology: Animal Behavior Processes. 1990;16:40–47. [PubMed] [Google Scholar]
- Corbit LH, Balleine BW. Double dissociation of basolateral and central amygdala lesions on the general and outcome-specific forms of pavlovian-instrumental transfer. Journal of Neuroscience. 2005;25:962–970. doi: 10.1523/JNEUROSCI.4507-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delamater AR. Outcome-selective effects of intertrial reinforcement in a Pavlovian appetitive conditioning paradigm with rats. Animal Learning & Behavior. 1995;23:31–39. [Google Scholar]
- Delamater AR. Selective reinstatement of stimulus-outcome associations. Animal Learning & Behavior. 1997;25:400–412. [Google Scholar]
- Delamater AR. Associative mediational processes in the acquired equivalence and distinctiveness of cues. Journal of Experimental Psychology: Animal Behavior Processes. 1998;24:467–482. [PubMed] [Google Scholar]
- Delamater AR. Extinction of Conditioned Flavor Preferences. Journal of Experimental Psychology: Animal Behavior Processes. 2007;33:160–171. doi: 10.1037/0097-7403.33.2.160. [DOI] [PubMed] [Google Scholar]
- Delamater AR. The role of the orbitofrontal cortex in sensory-specific encoding of associations in pavlovian and instrumental conditioning. Ann N Y Acad Sci. 2007b;1121:152–173. doi: 10.1196/annals.1401.030. [DOI] [PubMed] [Google Scholar]
- Delamater AR, Holland PC. The influence of CS-US interval on several different indices of learning in appetitive conditioning. Journal of Experimental Psychology: Animal Behavior Processes. 2008;34:202–222. doi: 10.1037/0097-7403.34.2.202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delamater AR, Joseph P. Common coding in symbolic matching tasks with humans: Training with a common consequence or antecedent. Quarterly Journal of Experimental Psychology: Comparative & Physiological Psychology. 2000;53B:255–274. doi: 10.1080/027249900411182. [DOI] [PubMed] [Google Scholar]
- Delamater AR, LoLordo VM. Event revaluation procedures and associative structures in Pavlovian conditioning. In: Dachowski L, Flaherty CF, editors. Current topics in animal learning: Brain, emotion, and cognition. Hillsdale, NJ: Lawrence Erlbaum Associates; 1991. pp. 55–94. [Google Scholar]
- Delamater AR, Oakeshott S. Learning about Multiple Attributes of Reward in Pavlovian Conditioning. Annual New York Academy of Science. 2007;1104:1–20. doi: 10.1196/annals.1390.008. [DOI] [PubMed] [Google Scholar]
- Delamater AR, Kranjec A, Fein M. Differential outcome effects in Pavlovian biconditional and ambiguous occasion setting tasks. Journal of Experimental Psychology: Animal Behavior Processes. 2010;36:471–481. doi: 10.1037/a0019136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delamater AR, LoLordo VM, Berridge KC. Control of fluid palatability by exteroceptive Pavlovian signals. Journal of Experimental Psychology Animal Behavior Processes. 1986;12:143–152. [PubMed] [Google Scholar]
- Delamater AR, Sosa W, Katz M. Elemental and configural processes in patterning discrimination learning. Quarterly Journal of Experimental Psychology: B. 1999;52:97–124. [Google Scholar]
- Desgranges B, Ramirez-Amaya V, Ricaño-Cornejo I, Levy F, Ferreira G. Flavor Preference Learning Increases Olfactory and Gustatory Convergence onto Single Neurons in the Basolateral Amygdala but Not in the Insular Cortex in Rats. Plos One. 2010;5:1–8. doi: 10.1371/journal.pone.0010097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickinson A, Dearing MF. Appetitive-aversive interactions and inhibitory processes. In: Dickinson A, Boakes RA, editors. Mechanisms of Learning and Motivation. Lawrence Erlbaum Associates; Hillsdale NJ: 1979. pp. 203–231. [Google Scholar]
- Dwyer DM. Microstructural analysis of conditioned and unconditioned responses to maltodextrin. Learning & Behavior. 2008;36:149–157. doi: 10.3758/lb.36.2.149. [DOI] [PubMed] [Google Scholar]
- Dwyer DM, Pincham HL, Thein T, Harris JA. A learned flavor preference persists despite the extinction of conditioned hedonic reactions to the cue flavors. Learning & Behavior. 2009;37:305–310. doi: 10.3758/LB.37.4.305. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gibbon J. Time, rate, and conditioning. Psychological Review. 2000;107:289–344. doi: 10.1037/0033-295x.107.2.289. [DOI] [PubMed] [Google Scholar]
- Gewirtz JC, Brandon SE, Wagner AR. Modulation of the acquisition of the rabbit eyeblink conditioned response by conditioned contextual stimuli. Journal of Experimental Psychology: Animal Behavior Processes. 1998;24:106–117. doi: 10.1037//0097-7403.24.1.106. [DOI] [PubMed] [Google Scholar]
- Gibbon J, Balsam PD. The spread of association in time. In: Locurto CM, Terrace HS, Gibbon J, editors. Autoshaping and conditioning theory. New York: Academic Press; 1981. [Google Scholar]
- Gibson JJ, Gibson EJ. Perceptual learning: Differentiation or enrichment? Psychological Review. 1955;62:32–41. doi: 10.1037/h0048826. [DOI] [PubMed] [Google Scholar]
- Gluck MA, Myers CE. Hippocampal mediation of stimulus representation: a computational theory. Hippocampus. 1993;3:491–516. doi: 10.1002/hipo.450030410. [DOI] [PubMed] [Google Scholar]
- Grand C, Honey RC. Solving XOR. J Exp Psychol Anim Behav Process. 2008;34:486–493. doi: 10.1037/0097-7403.34.4.486. [DOI] [PubMed] [Google Scholar]
- Hall G. Learning about associatively activated stimulus representations: Implications for acquired equivalence and perceptual learning. Animal Learning & Behavior. 1996;24:233–255. [Google Scholar]
- Hall G. Associative structures in Pavlovian and instrumental conditioning. In: Gallistel R, editor. Stevens’ handbook of experimental psychology Volume 3: Learning, Motivation, and Emotion. New York: John Wiley & Sons, Inc; 2002. pp. 1–45. [Google Scholar]
- Harris JA. Elemental representations of stimuli in associative learning. Psychol Rev. 2006;113(3):584–605. doi: 10.1037/0033-295X.113.3.584. [DOI] [PubMed] [Google Scholar]
- Harris JA, Gharaei S, Moore CA. Representations of single and compound stimuli in negative and positive patterning. Learn Behav. 2009;37(3):230–245. doi: 10.3758/LB.37.3.230. [DOI] [PubMed] [Google Scholar]
- Harris JA, Livesey EJ, Gharaei S, Westbrook RF. Negative patterning is easier than a biconditional discrimination. J Exp Psychol Anim Behav Process. 2008;34(4):494–500. doi: 10.1037/0097-7403.34.4.494. [DOI] [PubMed] [Google Scholar]
- Harris JA, Shand FL, Carroll LQ, Westbrook RF. Persistence of preference for a flavor presented in simultaneous compound with sucrose. Journal of Experimental Psychology: Animal Behavior Processes. 2004;30:177–189. doi: 10.1037/0097-7403.30.3.177. [DOI] [PubMed] [Google Scholar]
- Haselgrove M, Esber GR, Pearce JM, Jones PM. Two kinds of attention in Pavlovian conditioning: evidence for a hybrid model of learning. J Exp Psychol Anim Behav Process. 2010;36(4):456–470. doi: 10.1037/a0018528. [DOI] [PubMed] [Google Scholar]
- Haselgrove M, Robinson J, Nelson A, Pearce JM. Analysis of an ambiguous-feature discrimination. Quarterly Journal of Experimental Psychology. 2008;61:1710–1725. doi: 10.1080/17470210701680746. [DOI] [PubMed] [Google Scholar]
- Hearst E. The feature-positive effect in pigeons: Conditionality, overall predictiveness, and type of feature. Bulletin of the Psychonomic Society. 1984;26:73–76. [Google Scholar]
- Holland PC. The nature of conditioned inhibition in serial and simultaneous feature negative discriminations. In: Miller RR, Spear NE, editors. Information processing in animals: Conditioned inhibition. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc; 1985. pp. 267–298. [Google Scholar]
- Holland PC. Event representations in Pavlovian conditioning: Image and action. Cognition. 1990;37:105–131. doi: 10.1016/0010-0277(90)90020-k. [DOI] [PubMed] [Google Scholar]
- Holland PC. Transfer of control in ambiguous discriminations. J Exp Psychol Anim Behav Process. 1991;17:231–248. doi: 10.1037//0097-7403.17.3.231. [DOI] [PubMed] [Google Scholar]
- Holland P. Amount of training affects associatively-activated event representation. Neuropharmacology. 1998;37:461–469. doi: 10.1016/s0028-3908(98)00038-0. [DOI] [PubMed] [Google Scholar]
- Holland PC, Reeve CE. Acquisition and transfer of control by an ambiguous cue. Animal Learning & Behavior. 1991;19:113–124. [Google Scholar]
- Holland PC, Rescorla RA. The effect of two ways of devaluing the unconditioned stimulus after first- and second-order appetitive conditioning. J Exp Psychol Anim Behav Process. 1975;1(4):355–363. doi: 10.1037//0097-7403.1.4.355. [DOI] [PubMed] [Google Scholar]
- Holland PC, Lasseter H, Agarwal I. Amount of training and cue-evoked taste-reactivity responding in reinforcer devaluation. Journal of Experimental Psychology: Animal Behavior Processes. 2008;34:119–132. doi: 10.1037/0097-7403.34.1.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey RC. Associative priming in Pavlovian conditioning. Q J Exp Psychol B. 2000;53:1–23. doi: 10.1080/027249900392977. [DOI] [PubMed] [Google Scholar]
- Honey RC, Hall G. Acquired equivalence and distinctiveness of cues. J Exp Psychol Anim Behav Process. 1989;15:338–346. [PubMed] [Google Scholar]
- Honey RC, Ward-Robinson J. Transfer between contextual conditional discriminations: an examination of how stimulus conjuctions are represented. J Exp Psychol Anim Behav Process. 2001;27(3):196–205. [PubMed] [Google Scholar]
- Honey RC, Ward-Robinson J. Acquired equivalence and distinctiveness of cues: I. Exploring a neural network approach. J Exp Psychol Anim Behav Process. 2002;28:378–387. [PubMed] [Google Scholar]
- Honey RC, Close J, Lin TE. Acquired distinctiveness and equivalence: A synthesis. In: Mitchell CJ, Le Pelley ME, editors. Attention and associative learning: From brain to behaviour. Oxford: Oxford University Press; 2010. [Google Scholar]
- Jenkins HM, Sainsbury RS. The development of stimulus control through differential reinforcement. In: Mackintosh NJ, Honig WK, editors. Fundamental issues in associative learning. Halifax, NS, Canada: Dalhousie University Press; 1969. pp. 239–273. [Google Scholar]
- Kehoe EJ. A layered network model of associative learning: Learning to learn and configuration. Psychological Review. 1988;95(4):411–433. doi: 10.1037/0033-295x.95.4.411. [DOI] [PubMed] [Google Scholar]
- Kendler HH. “What is learned?” – A theoretical blind alley. Psychological Review. 1952;59:269–277. doi: 10.1037/h0057469. [DOI] [PubMed] [Google Scholar]
- Kerfoot EC, Agarwal I, Lee HJ, Holland PC. Control of appetitive and aversive taste-reactivity responses by an auditory conditioned stimulus in a devaluation task: a FOS and behavioral analysis. Learning & Memory. 2007;14(9):581–589. doi: 10.1101/lm.627007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim JJ, Krupa DJ, Thompson RF. Inhibitory cerebello-olivary projections and blocking effect in classical conditioning. Science. 1998;279(5350):570–573. doi: 10.1126/science.279.5350.570. [DOI] [PubMed] [Google Scholar]
- Konorski J. Integrative activity of the brain. Chicago: University of Chicago Press; 1967. [Google Scholar]
- Kruse JM, Overmier JB, Konz WA, Rokke E. Pavlovian conditioned stimulus effects upon instrumental choice behavior are reinforcer specific. Learning & Motivation. 1983;14(2):165–181. [Google Scholar]
- Mackintosh NJ. A theory of attention: Variation in the associability of stimuli with reinforcement. Psychological Review. 1975;82:276–298. [Google Scholar]
- McCloskey M, Cohen NJ. Catastrophic interference in connectionist networks: The sequential learning problem. In: Bower GH, editor. The psychology of learning and motivation. Vol. 24. New York: Academic Press; 1989. pp. 109–164. [Google Scholar]
- McLaren IPL, Mackintosh NJ. An elemental model of associative learning: I. Latent inhibition and perceptual learning. Animal Learning & Behavior. 2000;26:211–246. [Google Scholar]
- McLaren IPL, Mackintosh NJ. Associative learning and elemental representation: II. Generalization and discrimination. Anim Learn Behav. 2002;30(3):177–200. doi: 10.3758/bf03192828. [DOI] [PubMed] [Google Scholar]
- Nakajima S, Kobayashi H. Differential outcomes effect on instrumental serial feature-ambiguous discrimination in rats. The Psychological Record. 2000;50:189–198. [Google Scholar]
- O’Reilly RC. Biologically plausible error-driven learning using local activation differences: The generalized recirculation algorithm. Neural Computation. 1996;8:895–938. [Google Scholar]
- O’Reilly RC, Munakata Y. Computational explorations in cognitive neuroscience: Understanding the mind by simulating the brain. Cambridge, MA: MIT Press; 2000. [Google Scholar]
- O’Reilly RC, Rudy JW. Conjunctive representations in learning and memory: principles of cortical and hippocampal function. Psychol Rev. 2001;108(2):311–345. doi: 10.1037/0033-295x.108.2.311. [DOI] [PubMed] [Google Scholar]
- Ostlund SB, Balleine BW. Orbitofrontal Cortex Mediates Outcome Encoding in Pavlovian but not Instrumental Conditioning. The Journal of Neuroscience. 2007;27:4819–4825. doi: 10.1523/JNEUROSCI.5443-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostlund SB, Balleine BW. Differential Involvement of the Basolateral Amygdala and Mediodorsal Thalamus in Instrumental Action Selection. The Journal of Neuroscience. 2008;28:4398–4405. doi: 10.1523/JNEUROSCI.5472-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce JM. A model for stimulus generalization in Pavlovian conditioning. Psychological Review. 1987;94:61–73. [PubMed] [Google Scholar]
- Pearce JM. Similarity and discrimination: A selective review and a connectionist model. Psychological Review. 1994;101:587–607. doi: 10.1037/0033-295x.101.4.587. [DOI] [PubMed] [Google Scholar]
- Pearce JM. Evaluation and development of a connectionist theory of configural learning. Animal Learning & Behavior. 2002;30:73–95. doi: 10.3758/bf03192911. [DOI] [PubMed] [Google Scholar]
- Pearce JM, Hall G. A model for Pavlovian learning: Variations in the effectiveness of conditioned but not of unconditioned stimuli. Psychological Review. 1980;87:532–552. [PubMed] [Google Scholar]
- Pearce JM, Mackintosh NJ. Two theories of attention: A review and a possible integration. In: Le Pelley ME, Mitchell CJ, editors. Learning and attention. Oxford, England: Oxford University Press; 2010. [Google Scholar]
- Pearce JM, Redhead ES. The influence of an irrelevant stimulus on two discriminations. Journal of Experimental Psychology: Animal Behavior Processes. 1993;19:180–190. [Google Scholar]
- Pearce JM, Esber GR, George DN, Haselgrove M. The nature of discrimination learning in pigeons. Learning & Behavior. 2008;36:188–199. doi: 10.3758/lb.36.3.188. [DOI] [PubMed] [Google Scholar]
- Poremba A, Saunders RC, Crane AM, Cook M, Sokoloff L, Mishkin M. Functional mappinjg of the primate auditory system. Science. 2003;299:568–572. doi: 10.1126/science.1078900. [DOI] [PubMed] [Google Scholar]
- Redhead ES, Pearce JM. Stimulus salience and negative patterning. Quarterly Journal of Experimental Psychology (B): Comparative and Physiological Psychology. 1995;48B:67–83. [PubMed] [Google Scholar]
- Rescorla RA. Stimulus generalization: Some predictions from a model of Pavlovian conditioning. Journal of Experimental Psychology: Animal Behavior Processes. 1976;2(1):88–96. doi: 10.1037//0097-7403.2.1.88. [DOI] [PubMed] [Google Scholar]
- Rescorla RA. Simultaneous associations. In: Harzem P, Zeiler M, editors. Advances in analysis of behavior. 2. New York: Wiley; 1980. [Google Scholar]
- Rescorla RA. Pavlovian second-order conditioning: Studies in associative learning. Hillsdale, NJ: Lawrence Erlbaum Associates; 1980. [Google Scholar]
- Rescorla RA. Conditioned inhibition and facilitation. In: Miller RR, Spear NE, editors. Information processing in animals: Conditioned inhibition. Hillsdale, NJ: Erlbaum; 1985. pp. 299–326. [Google Scholar]
- Rescorla RA. Summation and overexpectation with qualitatively different outcomes. Animal Learning & Behavior. 1999;27(1):50–62. [Google Scholar]
- Rescorla RA, Solomon RL. Two-process learning theory: relationship between Pavlovian conditioning and instrumental learning. Psychological Review. 1967;74:151–182. doi: 10.1037/h0024475. [DOI] [PubMed] [Google Scholar]
- Rescorla RA, Wagner AR. A theory of Pavlovian conditioning: Variations in the effectiveness of reinforcement and nonreinforcement. In: Black AH, Prokasy WF, editors. Classical conditioning II: Current research and theory. New York: Appleton-Century-Crofts; 1972. pp. 64–99. [Google Scholar]
- Rozeboom WW. “What is learned?”: An empirical enigma. Psychological Review. 1958;65:22–33. doi: 10.1037/h0045256. [DOI] [PubMed] [Google Scholar]
- Rumelhart DE, McClelland JL the PDP Research Group. Parallel distributed processing: Explorations in the microstructure of cognition. Cambridge, MA: The MIT Press; 1986. [Google Scholar]
- Rumelhart DE, Hinton GE, Williams RJ. the PDP Research Group. Learning internal representations by error propagation. In: Rumelhart DE, McClelland JL, editors. Parallel distributed processing: Explorations in the microstructure of cognition. Vol. 1: Foundations. Cambridge, MA: MIT Press; 1986. pp. 318–362. [Google Scholar]
- Saddoris MP, Holland PC, Gallagher M. Associatively Learned Representations of Taste Outcomes Activate Taste-Encoding Neural Ensembles in Gustatory Cortex. The Journal of Neuroscience. 2009;29:15386–15396. doi: 10.1523/JNEUROSCI.3233-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmajuk NA, DiCarlo JJ. Stimulus configuration, classical conditioning, and hippocampal function. Psychol Rev. 1992;99:268–305. doi: 10.1037/0033-295x.99.2.268. [DOI] [PubMed] [Google Scholar]
- Schmajuk NA, Lamoureux JA, Holland PC. Occasion setting: A neural network approach. Psychological Review. 1998;105(1):3–32. doi: 10.1037/0033-295x.105.1.3. [DOI] [PubMed] [Google Scholar]
- Smith KS, Berridge KC, Aldridge JW. Disentangling pleasure from incentive salience and learning signals in brain reward circuitry. Proceedings of the National Academy of Sciences. 2011 doi: 10.1073/pnas.1101920108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner AR. Expectancies and the priming of STM. In: Hulse SH, Fowler H, Honig WK, editors. Cognitive processes in animal behavior. Hillsdale, NJ: Erlbaum; 1978. pp. 177–209. [Google Scholar]
- Wagner AR. Context-sensitive elemental theory. Q J Exp Psychol B. 2003;56(1):7–29. doi: 10.1080/02724990244000133. [DOI] [PubMed] [Google Scholar]
- Wagner AR. Evolution of an elemental theory of Pavlovian conditioning. Learn Behav. 2008;36:253–265. doi: 10.3758/lb.36.3.253. [DOI] [PubMed] [Google Scholar]
- Wagner AR, Brandon SE. Evolution of a structured connectionist model of Pavlovian conditioning (AESOP) In: Klein SB, Mowrer RR, editors. Contemporary learning theories: Pavlovian conditioning and the status of traditional learning theory. Hillsdale, NJ: Erlbaum; 1989. pp. 149–189. [Google Scholar]
- Wagner AR, Brandon SE. A componential theory of Pavlovian conditioning. In: Mowrer RR, Klein SB, editors. Handbook of contemporary learning theories. Mahwah, NJ: Lawrence Erlbaum Associates, Inc., Publishers; 2001. pp. 23–64. [Google Scholar]
- Watt A, Honey RC. Combining CSs associated with the same or different USs. Q J Exp Psychol B. 1997;50(4):350–367. doi: 10.1080/713932659. [DOI] [PubMed] [Google Scholar]
- Williams DA, Mehta R, Poworoznyk TM, Orihel JS, George DN, Pearce JM. Acquisition of superexcitatory properties by an irrelevant background stimulus. Journal of Experimental Psychology: Animal Behavior Processes. 2002;28:284–297. [PubMed] [Google Scholar]
- Zentall TR, Steirn JN, Sherburne LM, Urcuioli PJ. Common coding in pigeons assessed through partial versus total reversals of many-to-one conditional and simple discriminations. Journal of Experimental Psychology: Animal Behavior Processes. 1991;17:194–201. [Google Scholar]