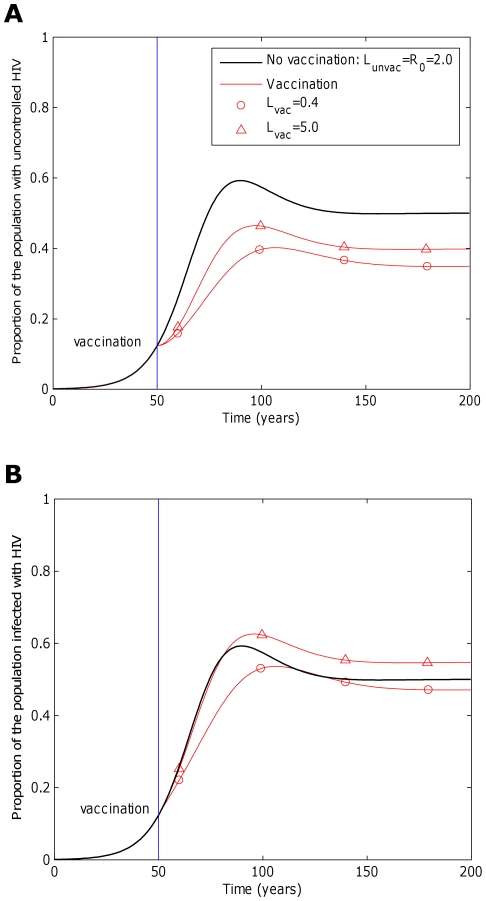
Figure 2. The impact of a CTL-based vaccine is dependent upon the extent to which it affects transmission potential.
This figure considers the impact that a five-epitope vaccine could have on an epidemic. Two measurements are considered: A) the proportion of hosts in the population with uncontrolled infections and B) the proportion of hosts who are infected. In each panel two vaccines with different average transmission potentials are explored and compared to the scenario when the vaccine is absent (black line). Our simulations are based upon an epidemic in a sub-saharan community, thus we assume a basic reproductive number of 2 in the absence of vaccination (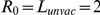 ,
,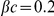 ,
,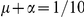 years−1). One vaccine (circles, A and B) considerably reduces transmission probability by a factor of 25 (
years−1). One vaccine (circles, A and B) considerably reduces transmission probability by a factor of 25 (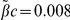 ), but restores life expectancy to its normal value (50 years;
), but restores life expectancy to its normal value (50 years; 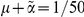 years−1). This vaccine reduces transmission potential by a factor of 5 (from
years−1). This vaccine reduces transmission potential by a factor of 5 (from 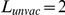 to
to 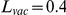 ). The second example vaccine (triangles, A and B) causes a modest two fold reduction in transmission probability (
). The second example vaccine (triangles, A and B) causes a modest two fold reduction in transmission probability (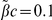 ) and restores life expectancy to the its uninfected value (
) and restores life expectancy to the its uninfected value (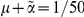 ). Thus, this vaccine more than doubles the transmission potential (
). Thus, this vaccine more than doubles the transmission potential (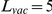 ). In both cases the vaccine is administered to all unvaccinated hosts 50 years into the epidemic and to all newborns (γ = 1) thereafter, but provides no level of sterilizing immunity (r = 0). This figure shows that a vaccine that reduces the transmission potential (
). In both cases the vaccine is administered to all unvaccinated hosts 50 years into the epidemic and to all newborns (γ = 1) thereafter, but provides no level of sterilizing immunity (r = 0). This figure shows that a vaccine that reduces the transmission potential (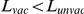 ) – i.e. suppresses infectiousness by a greater factor than it increases life expectancy – would reduce both the proportion of hosts with uncontrolled HIV (circles, A) and the proportion of hosts infected with HIV (circles, B). A vaccine that reduces transmission potential (
) – i.e. suppresses infectiousness by a greater factor than it increases life expectancy – would reduce both the proportion of hosts with uncontrolled HIV (circles, A) and the proportion of hosts infected with HIV (circles, B). A vaccine that reduces transmission potential (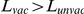 ) would also decrease the proportion of hosts with uncontrolled HIV (triangles, A), but would marginally increase the proportion of hosts infected with HIV (triangles, B). For these figures we assume that the vaccine elicits responses to five CTL epitopes. At each epitope escape in HLA matched hosts escape takes an average 8 years following infection (
) would also decrease the proportion of hosts with uncontrolled HIV (triangles, A), but would marginally increase the proportion of hosts infected with HIV (triangles, B). For these figures we assume that the vaccine elicits responses to five CTL epitopes. At each epitope escape in HLA matched hosts escape takes an average 8 years following infection (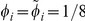 years−1 for i = 1∶5). Reversion in HLA mismatched hosts takes an average of 36 years at each epitope (
years−1 for i = 1∶5). Reversion in HLA mismatched hosts takes an average of 36 years at each epitope (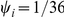 years−1 for i = 1∶5). We also assume that at the start of the epidemic 0.1% of the population are infected and that all of these hosts are infected with the wildytype strain.
years−1 for i = 1∶5). We also assume that at the start of the epidemic 0.1% of the population are infected and that all of these hosts are infected with the wildytype strain.