Functional regression via variational Bayes

Abstract

We introduce variational Bayes methods for fast approximate inference in functional regression analysis. Both the standard cross-sectional and the increasingly common longitudinal settings are treated. The methodology allows Bayesian functional regression analyses to be conducted without the computational overhead of Monte Carlo methods. Confidence intervals of the model parameters are obtained both using the approximate variational approach and nonparametric resampling of clusters. The latter approach is possible because our variational Bayes functional regression approach is computationally efficient. A simulation study indicates that variational Bayes is highly accurate in estimating the parameters of interest and in approximating the Markov chain Monte Carlo-sampled joint posterior distribution of the model parameters. The methods apply generally, but are motivated by a longitudinal neuroimaging study of multiple sclerosis patients. Code used in simulations is made available as a web-supplement.

1. Introduction

Due to ever-expanding methods for the acquisition and storage of information, functional data is often encountered in scientific applications. A common problem in the field of functional data analysis is determining the relationship between a scalar outcome Y and a densely observed functional predictor X(t) [18, 22, 9]. Increasingly, this problem is longitudinal in that both the functional predictors and scalar outcomes are observed at several visits for each subject. Bayesian approaches to cross-sectional and longitudinal functional regression possess a number of advantages, including the ability to jointly model the observed functions and scalar outcomes and easily constructed credible intervals [5, 7]. However, these approaches require computationally expensive Markov chain Monte Carlo (MCMC) simulations of joint posterior distributions. The goal of this paper is to introduce a fast and scalable alternative to accommodate new types of data sets.

Variational approximations, now regularly used in computer science, are a collection of techniques for deriving approximate solutions to inference problems [10, 11, 25]. They have a growing visibility in the statistics literature [16, 19, 24]. In the Bayesian context, these methods are useful in approximating intractable posterior density functions. While this approximation sacrifices some of MCMC’s accuracy, it provides large gains in terms of computational feasibility, especially in large-data settings.

In this article, we derive an iterative algorithm for approximate Bayesian inference in functional regression. Using this algorithm, inference on model parameters can be obtained several orders of magnitude faster than MCMC sampling methods. Importantly, the construction of credible intervals for the functional coefficient is straightforward. Moreover, this procedure retains the ability to jointly model the predictor process and the scalar outcome. The computational advantage conveyed by the variational methods also allows resampling techniques, such as the nonparametric bootstrap of subjects, to be used. Unlike MCMC sampling, the variational approach cannot be made arbitrarily accurate. However, simulations indicate that the quality of the approximation is high in our setting. Our variational method is not designed to replace MCMC sampling, but it is a useful additional inferential tool in that it provides near-instant and highly accurate approximate posterior distributions. This will become increasingly relevant as functional datasets become larger and more complex.

In particular, we develop variational Bayes methods for two functional regression models: the classic cross-sectional case, in which a single scalar outcome and functional predictor are observed for each subject; and the more recent longitudinal case, in which scalar outcomes and functional predictors are observed repeatedly for each subject. This methodology is based on a penalized approach to functional regression that is flexible and widely applicable [6]. Although variational techniques typically incur initial algebraic and implementation costs, the present article alleviates these considerations.

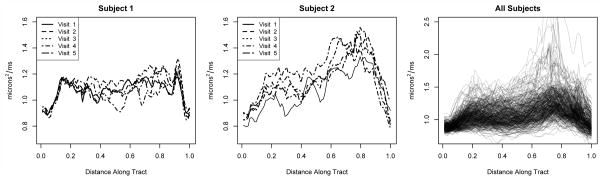
We apply the methods developed to a longitudinal neuroimaging study, in which multiple sclerosis patients undergo both tests of cognitive ability and a diffusion tensor imaging scan at each of several visits. From the diffusion tensor imaging scans, we construct functional predictors that provide detailed quantitative information about major white matter fiber bundles (see Figure 1). Because multiple sclerosis results in the degradation of cerebral white matter, researchers hope to use the functional predictors and cognitive disability measures to understand the progression of the disease. This study was previously analyzed in [7].

Fig 1.

The functional predictor used in our diffusion tensor imaging application. The left and middle panels show the functional predictors observed for individual subjects; the right panel shows the collection of all observed functions.

In Section 2 we introduce variational Bayes and a penalized approach to functional regression. Section 3 combines these ideas and develops a scalable iterative algorithm for approximate Bayesian inference in functional regression. The results of a simulation study are described in Section 4 and a real-data analysis is performed in Section 5. We conclude the main text with a discussion in Section 6. Appendices A and B contain algebraic derivations and expressions used in the construction of the iterative algorithm. All code used in the simulation study is available as a web-supplement to this article.

2. Background

In the following subsections we introduce variational approximations for Bayesian inference and an approach to functional regression which uses penalized B-splines to estimate the coefficient function.

2.1. Variational Bayes

Here we give an overview of variational Bayes; for a more complete treatment see [19] and [3], Chapter 10.

Bayesian inference is based on the posterior density function

$$p(\mathit{\theta }\mid \mathit{y})=\frac{p(\mathit{y},\mathit{\theta })}{p(\mathit{y})}$$

where θ ∈ Θ is the parameter vector, y is the observed data, p(y) is the marginal likelihood of the observed data, and p(y, θ) is the joint likelihood of the data and model parameters. The goal of the density transform approach is to approximate the posterior density p(θ|y) by a function q(θ) for which the q-specific lower bound on the marginal likelihood (defined below) is more tractable than the marginal likelihood itself. The first step is to restrict q to a more manageable class of densities and choose the element of that class with minimum Kullback-Leibler distance from p(θ|y).

More concretely, let q be an arbitrary density function over Θ. Then

$$logp(\mathit{y})\ge \int q(\mathit{\theta })log\left\{\frac{p(\mathit{y},\theta )}{q(\mathit{\theta })}\right\}d\mathit{\theta }.$$ (2.1)

with equality if and only if q(θ) = p(θ|y) almost everywhere [12]. It follows that $p(\mathit{y})\ge exp\int q(\mathit{\theta })log\left\{\frac{p(\mathit{y},\theta )}{q(\mathit{\theta })}\right\}d\mathit{\theta }$; we define the q-specific lower bound on the marginal likelihood as

$$\underset{\_}{p}(\mathit{y};q)\equiv exp\int q(\mathit{\theta })log\left\{\frac{p(\mathit{y},\theta )}{q(\mathit{\theta })}\right\}d\mathit{\theta }.$$ (2.2)

It can be shown that minimizing the Kullback-Leibler distance between q(θ) and p(θ|y) is equivalent to maximizing p(y; q). Stated generally, the following result holds.

Result 2.1

Let u and v be continuous random vectors with joint density p(u, v). Then

$$su{p}_q\left\{\int q(\mathit{u})log\left[\frac{p(\mathit{u},\mathit{v})}{q(\mathit{u})}d\mathit{u}\right]\right\}$$

is achieved by q^*(u) = p(u|v).

Next, we restrict q to a class of functions for which p(y; q) is more tractable than p(y). While several restrictions are possible, here we focus on the product density transform: we assume that for some partition {θ₁, …, θ_L} of θ it is possible to write $q(\mathit{\theta })={\prod }_{l=1}^L{q}_l({\mathit{\theta }}_l)$. In the functional regression setting, the posterior dependence of some subsets of the model parameters is weak and the assumption that q factorizes provides accurate approximate inference. In other settings where the posterior dependence of parameters is stronger, this assumption may lead to poor approximations and inference due to the failure to account for correlations between model parameters. There are three simple strategies to gain insight into what sets of parameters are a-posteriori weakly correlated: 1) theoretical work on asymptotic posterior correlations; 2) Bayesian inference on smaller or simpler data sets; and 3) prior experience. If posterior correlation is potentially problematic, a more flexible component density q_l that allows for this correlation could be used; however, this must be balanced against the simplification desired in the approximating class of functions. While none of the approaches above is infallible, when combined with powerful variational approximations they can provide a valuable alternative to Bayesian inference. The methods provided in this paper are intended as a reasonable and tractable complement of and not replacement for Bayesian computations.

Combining the assumption that q factorizes over a partition of θ with Result 2.1, we can derive explicit solutions for each factor q_l(θ_l), 1 ≤ l ≤ L, in terms of the remaining factors. Solving for each factor in terms of the others leads to an iterative algorithm for obtaining a solution for q. The explicit solution for each q_l(θ_l) is derived as follows. Assuming that q is subject to the factorization restriction, it follows that

$$\begin{array}{l}log\underset{\_}{p}(\mathit{y};q)=\int \left(\prod _{l=1}^L{q}_i({\mathit{\theta }}_i)\right)\left(logp(\mathit{y},\mathit{\theta })-\sum _{l=1}^{L}log{q}_i({\mathit{\theta }}_i)\right)d{\mathit{\theta }}_1\dots d{\mathit{\theta }}_L\\ =\int q_1({\mathit{\theta }}_1)\left(\int logp(\mathit{y},\mathit{\theta })q_2({\mathit{\theta }}_2)\dots q_L({\mathit{\theta }}_L)d{\mathit{\theta }}_2\dots d{\mathit{\theta }}_L\right)d{\mathit{\theta }}_1-\int q_1({\mathit{\theta }}_1)log{q}_1({\mathit{\theta }}_1)d{\mathit{\theta }}_1+\text{terms}\text{not}\text{involving}{q}_1\end{array}$$

Define the joint density function p̃ (y, θ₁) to be

$$\stackrel{\sim }{p}(\mathit{y},{\mathit{\theta }}_1)\equiv \frac{exp\int logp(\mathit{y},\mathit{\theta })q_2({\mathit{\theta }}_2)\cdots q_M({\mathit{\theta }}_M)d{\mathit{\theta }}_2\cdots d{\mathit{\theta }}_M}{\int \int \{exp\int logp(\mathit{y},\mathit{\theta })q_2({\mathit{\theta }}_2)\cdots q_M({\mathit{\theta }}_M)d{\mathit{\theta }}_2\cdots d{\mathit{\theta }}_M\}d{\mathit{\theta }}_{1}d\mathit{y}}$$

so that

$$log\underset{\_}{p}(\mathit{y};q)=\int q_1({\mathit{\theta }}_1)log\left[\frac{\stackrel{\sim }{p}(\mathit{y},{\mathit{\theta }}_1)}{q_1({\mathit{\theta }}_1)}\right]+\text{terms}\text{not}\text{involving}{q}_1.$$

Then, using Result 2.1, the optimal q₁ is

$$\begin{array}{l}{q}_1^{\ast }({\mathit{\theta }}_1)=\stackrel{\sim }{p}({\mathit{\theta }}_1\mid \mathit{y})=\frac{\stackrel{\sim }{p}(\mathit{y},{\mathit{\theta }}_1)}{\int \stackrel{\sim }{p}(\mathit{y},{\mathit{\theta }}_1)d{\mathit{\theta }}_1}\\ \propto exp\left[\int logp(\mathit{y},\theta )q_2({\mathit{\theta }}_2)\dots q_L({\mathit{\theta }}_L)d{\mathit{\theta }}_2\dots d{\mathit{\theta }}_L\right]\\ =exp[E_{{\mathit{\theta }}_{-1}}logp(\mathit{y},\mathit{\theta })]\end{array}$$

where E_θ−1 log p(y, θ) is the expectation with respect to q₂(θ₂) … q_L(θ_L). The same argument for l in 1, …, L yields optimal densities satisfying

$$q_l^{\ast }({\mathit{\theta }}_l)\propto exp[E_{{\mathit{\theta }}_{-l}}logp(\mathit{y},\mathit{\theta })]\propto exp[E_{{\mathit{\theta }}_{-l}}logp({\mathit{\theta }}_l\mid \text{rest})]$$ (2.3)

where rest ≡ {y, θ₁, …, θ_l−1, θ_l+1, …, θ_L} is the collection of all remaining parameters and the observed data. Solving for each factor in terms of the others leads to an iterative algorithm for obtaining a solution for q. We update each factor in turn until the change in p(y; q) is negligible.

2.2. Penalized functional regression

Next we introduce penalized approaches to cross-sectional and longitudinal functional regression [5, 6, 7].

In the cross-sectional case, we observe data of the form [Y_i, X_i(t), z_i] for subjects 1 ≤ i ≤ I, where Y_i is a continuous outcome, X_i(t) is a functional covariate, and z_i is a 1 × p vector of non-functional covariates. The linear functional regression model is given by [4, 21]

$$\begin{array}{l}{Y}_i={\mathit{z}}_i\mathit{\beta }+{\int }_0^1{X}_i(t)\gamma (t)dt+{\epsilon }_i^Y\\ {\epsilon }_i^Y\sim \text{N}(0,{\sigma }_Y^2).\end{array}$$ (2.4)

We call the parameter γ(t) the coefficient function. In practice, the predictor functions X_i(t) are observed over a discrete grid, and often with error. That is, we observe {W_i(t_ij): t_ij ∈ [0, 1]} for 1 ≤ i ≤ I and 1 ≤ j ≤ J_i, where $W_i(t_{ij})=X_i(t_{ij})+{\epsilon }_i^X(t_{ij})$ and ${\epsilon }_i^X(t_{ij})\sim \text{N}(0,{\sigma }_X^2)$. The sampling scheme on which the functional predictors are observed may take a variety of forms: points may be equally or unequally spaced, sparse or dense at the subject level, identical or different across subjects. For simplicity, we will assume that all subjects are observed over the same grid {t₁, …, t_N } and are observed at an equal number of visits J. Extensions to different grids and different number of visits is straightforward, but with considerable increase in notational complexity.

To estimate the parameters in model (2.4), we use the following two-stage procedure. First, the predictor functions X_i(t) are expressed using a principal components (PC) decomposition. Second, the coefficient function γ(t) is estimated using penalized B-splines. Smoothness of γ̂(t) is explicitly induced via a mixed effects model. Specifically, let Σ̂^X(s, t) be an estimator of the covariance operator Cov (X_i(s), X_i(t)) based on the available functional observations. Further, let ${\sum }_{k=1}^{\infty }{\lambda }_k{\psi }_k(s){\psi }_k(t)$ be the spectral decomposition of Σ̂^X(s, t), where λ₁ ≥ λ₂ ≥ · · · are the non-increasing eigenvalues and ψ(t) = {ψ_k(t): k ∈ Z⁺} are the corresponding orthonormal eigenfunctions. An approximation for X_i(t), based on a truncated Karhunen-Lóeve expansion, is given by $X_i(t)=\mu (t)+{\sum }_{k=1}^{K_x}{c}_{ik}{\psi }_k(t)$, where K_x is the truncation lag, the PC loadings $c_{ik}={\int }_0^1\{X_i(t)-\mu (t)\}{\psi }_k(t)dt$ are uncorrelated random variables with variance λ_k, and μ(t) is the mean function over all subjects and visits.

Next, we use a large cubic B-spline basis to smoothly estimate the coefficient function γ(t) using a mixed effects model. Let φ(t) = {φ₁(t), …, φ_Kg(t)} be a cubic B-spline basis of dimension K_g. Then the integral in model (2.4) can be written as ${\int }_0^1{X}_i(t)\gamma (t)dt=a+{\int }_0^1{\mathit{c}}_i^{\prime }{\mathit{\psi }}^T(t)\mathit{\phi }(t)\mathit{g}dt=a+{\mathit{c}}_i^{\prime }\mathit{Mg}$ where $a={\int }_0^1\mu (t)\gamma (t)dt,{\mathit{c}}_i^{\prime }=[c_{i1},\dots ,c_{i{K}_x}]$ is the row vector of subject i’s PC loadings, and M is a K_x × K_g matrix with (k, l)^th entry ${\int }_0^1{\psi }_k(t){\phi }_l(t)dt$. Smoothness of γ̂(t) is enforced by assuming a modified first order random walk prior on the vector g [13]. That is, we assume $g_l\sim \text{N}(g_{l-1},{\sigma }_{\mathit{g}}^2)$ for 2 ≤ l ≤ K_g and let $g_1\sim \text{N}(0,0.01{\sigma }_{\mathit{g}}^2)$. These are standard assumptions in Bayesian P-splines modeling [23, 13]. Taken together, we jointly model the scalar outcome Y_i and the functional exposure X_i(t) using the following model:

$$\begin{array}{lll}{Y}_i\hfill & \sim \hfill & \text{N}({\mathit{z}}_i\mathit{\beta }+{\mathit{c}}_i^{\prime }\mathit{Mg},{\sigma }_{\mathit{Y}}^2);{\sigma }_{\mathit{Y}}^2\sim \text{IG}(A_{\mathit{Y}},B_{\mathit{Y}})\hfill \\ W_i(t)\hfill & \sim \hfill & \text{N}(\mu (t)+{\mathit{c}}_i^{\prime }\mathit{\psi }{(t)}^T,{\sigma }_{\mathit{X}}^2\mathit{I});{\sigma }_{\mathit{X}}^2\sim \text{IG}(A_{\mathit{X}},B_{\mathit{X}})\hfill \\ {\mathit{c}}_i^{\prime }\hfill & \sim \hfill & \text{N}(0,\mathrm{\Lambda });{\lambda }_k\sim \text{IG}(A_{\lambda },B_{\lambda })\text{for}1\le k\le K_x\hfill \\ \mathit{g}\hfill & \sim \hfill & \text{N}(0,{\sigma }_{\mathit{g}}^2\mathit{D});{\sigma }_{\mathit{g}}^2\sim \text{IG}(A_{\mathit{g}},B_{\mathit{g}})\hfill \\ \mathit{\beta }\hfill & \sim \hfill & \text{N}\left(0,{\sigma }_{\mathit{\beta }}^2\mathit{I}\right)\hfill \end{array}$$ (2.5)

where β are treated as fixed parameters with diffuse priors, D is the covariance matrix induced by the first order random walk prior, and Λ = diag[λ₁, …, λ_Kx]. Inference for the functional regression model is based on the posterior density

$$p(\mathit{g},\mathit{C},\mathit{\beta },{\sigma }_{\mathit{Y}}^2,{\sigma }_{\mathit{X}}^2,{\sigma }_{\mathit{g}}^2,{\lambda }_1,\dots ,{\lambda }_{K_x}\mid \mathit{Y},\mathit{W})$$ (2.6)

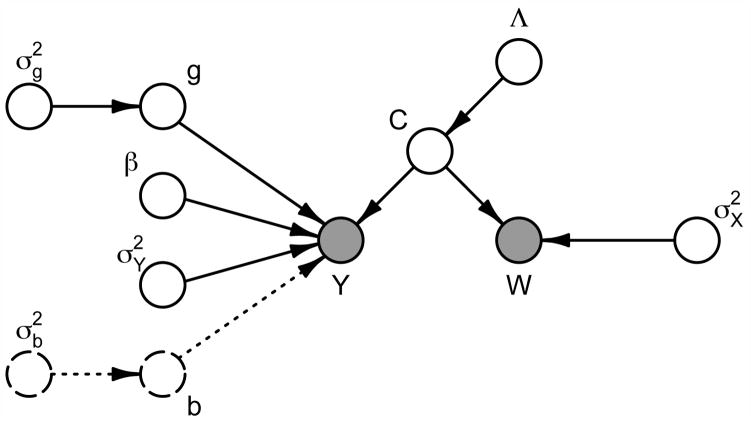
where C is the matrix of PC loadings constructed by row-stacking the c_i, $\mathit{Y}={\left\{Y_i\right\}}_{i=1}^I$, and W is the matrix of observed predictor functions constructed by row-stacking the W_i(t). Because the functional predictors X_i(t) are observed with error, this model extends Bayesian inference for measurement error regression problems to the functional setting. A directed acyclic graph depicting model (2.5) is presented in Figure 2.

Fig 2.

Directed acyclic graph corresponding to the functional regression model (2.5). Shaded nodes correspond to observed data, and unshaded nodes to model parameters. Arrows indicate conditional dependence. The nodes for ${\sigma }_{\mathit{b}}^2$ and b, shown as dashed lines, appear in the longitudinal functional regression model (2.8) but not in the cross-sectional model (2.5).

In the longitudinal case, we observe data of the form [Y_ij, X_ij(t), z_ij] for 1 ≤ i ≤ I and 1 ≤ j ≤ J_i. Thus we observe a distinct functional predictor and scalar outcome for each subject over several visits, and again note that in place of the true functional predictors X_ij(t) we often observe a measured-with-error function W_ij(t). The longitudinal functional regression model is given by [7]

$$\begin{array}{l}{Y}_{ij}={\mathit{Z}}_i\mathit{b}+{\mathit{z}}_{ij}\mathit{\beta }+{\int }_0^1{X}_{ij}(t)\gamma (t)dt+{\epsilon }_{ij}^Y\\ {\epsilon }_i^Y\sim \text{N}(0,{\sigma }_Y^2);\end{array}$$ (2.7)

this differs from model (2.4) in the use of subject-specific random effects Z_i to account for correlation in the repeated outcomes at the subject level. Moreover, longitudinal data sets tend to be much larger than cross-sectional data sets because of the number of visits.

Given the advent of multiple observational studies collecting dense functional data at multiple visits, the importance of longitudinal functional regression cannot be understated. Unfortunately, with the exception of the work in [7], no other approach can currently deal with the combination of subject-specific random effects and functional predictors necessary to capture the structure of the data. While a wide array of functional regression methods exist, we contend that the specific modeling choices described here made the extension not only possible, but seamless. Estimation of the parameters in the longitudinal setting extends naturally from the procedure outlined for the cross-sectional setting. Again, we express the functional predictors using a PC basis and use a penalized B-spline expansion for the coefficient function. The joint model for the outcome, Y_ij, and exposure, X_ij(t), becomes

$$\begin{array}{lll}{Y}_{ij}\hfill & \sim \hfill & \text{N}({\mathit{Z}}_i\mathit{b}+{\mathit{z}}_{ij}\mathit{\beta }+{\mathit{c}}_{ij}^{\prime }\mathit{Mg},{\sigma }_{\mathit{Y}}^2);{\sigma }_{\mathit{Y}}^2\sim \text{IG}(A_{\mathit{Y}},B_{\mathit{Y}})\hfill \\ W_{ij}(t)\hfill & \sim \hfill & \text{N}(\mu (t)+{\mathit{c}}_{ij}^{\prime }\mathit{\psi }{(t)}^T,{\sigma }_{\mathit{X}}^2\mathit{I});{\sigma }_{\mathit{X}}^2\sim \text{IG}(A_{\mathit{X}},B_{\mathit{X}})\hfill \\ {\mathit{c}}_{ij}^{\prime }\hfill & \sim \hfill & \text{N}(0,\mathrm{\Lambda });{\lambda }_k\sim \text{IG}(A_{\lambda },B_{\lambda })\text{for}1\le k\le K_x\hfill \\ \mathit{g}\hfill & \sim \hfill & \text{N}(0,{\sigma }_{\mathit{g}}^2\mathit{D});{\sigma }_{\mathit{g}}^2\sim \text{IG}(A_{\mathit{g}},B_{\mathit{g}})\hfill \\ \mathit{b}\hfill & \sim \hfill & \text{N}(0,{\sigma }_{\mathit{b}}^2\mathit{I});{\sigma }_{\mathit{b}}^2\sim \text{IG}(A_{\mathit{b}},B_{\mathit{b}})\hfill \\ \mathit{\beta }\hfill & \sim \hfill & \text{N}\left(0,{\sigma }_{\mathit{\beta }}^2\mathit{I}\right)\hfill \end{array}$$ (2.8)

Again, inference is based on the posterior density

$$p(\mathit{g},\mathit{C},\mathit{\beta },\mathit{b},{\sigma }_{\mathit{Y}}^2,{\sigma }_{\mathit{X}}^2,{\sigma }_{\mathit{g}}^2,{\sigma }_{\mathit{b}}^2,{\lambda }_1,\dots ,{\lambda }_{K_x}\mid \mathit{Y},\mathit{W})$$ (2.9)

A directed acyclic graph of the longitudinal functional regression model appears in Figure 2.

3. Variational approximations for penalized functional regression

We now combine the ideas introduced above to develop a scalable iterative algorithm for approximate Bayesian inference in functional regression. We will focus on the longitudinal functional regression model (2.8); the cross-sectional case can be obtained as a special case by omitting the vector of subject-specific random effects b. We pause briefly to introduce the following useful notation: for a scalar random variables θ, let

$$\begin{array}{l}{\mu }_{q(\theta )}\equiv {\text{E}}_q[\theta ]=\int {\theta }_{0}q({\theta }_0)d{\theta }_0\\ {\sigma }_{q(\theta )}\equiv {\text{Var}}_q[\theta ]=\int {({\theta }_0-\text{E}[\theta ])}^{2}q({\theta }_0)d{\theta }_0\end{array}$$

be the mean and variance with respect to the q distribution. For a vector parameter θ, we use the analogously defined μ_q(θ) and Σ_q(θ).

As noted, inference in the longitudinal functional regression model is based on the posterior density (2.9). Using variational Bayes, we approximate this posterior density using

$$q(\mathit{g},\mathit{C},\mathit{\beta },\mathit{b},{\sigma }_{\mathit{Y}}^2,{\sigma }_{\mathit{X}}^2,{\sigma }_{\mathit{g}}^2,{\sigma }_{\mathit{b}}^2,{\lambda }_1,\dots ,{\lambda }_{K_x})=q(\mathit{g})q(\mathit{C})q(\mathit{\beta })q(\mathit{b})q({\sigma }_{\mathit{Y}}^2,{\sigma }_{\mathit{X}}^2,{\sigma }_{\mathit{g}}^2,{\sigma }_{\mathit{b}}^2,{\lambda }_1,\dots ,{\lambda }_{K_x})$$ (3.1)

and by solving for each factor q(·) in terms of the remaining factors. The additional factorization

$$q({\sigma }_{\mathit{Y}}^2,{\sigma }_{\mathit{X}}^2,{\sigma }_{\mathit{g}}^2,{\sigma }_{\mathit{b}}^2,{\lambda }_1,\dots ,{\lambda }_{K_x})=q({\sigma }_{\mathit{Y}}^2)q({\sigma }_{\mathit{X}}^2)q({\sigma }_{\mathit{g}}^2)q({\sigma }_{\mathit{b}}^2)\prod _{j=1}^{K_x}q({\lambda }_j)$$

follows as a consequence of (2.3) and the structure of the current model as shown in Figure 2 [3, Sec. 10.2.5]. We take advantage of this induced factorization in deriving optimal densities for the variance components in the penalized functional regression model.

To provide an example of how optimal densities are constructed, we derive the optimal densities q^*(g) and $q^{\ast }({\sigma }_{\mathit{g}}^2)$; derivations of these and for the other parameters are provided in Appendix A. Recall that $\mathit{g}\sim \text{N}(0,{\sigma }_{\mathit{g}}^2\mathit{D})$ and ${\sigma }_{\mathit{g}}^2\sim \text{IG}(A_{\mathit{g}},B_{\mathit{g}})$. According to (2.3), the optimal densities are given by

$$q^{\ast }(\mathit{g})\propto exp\{E_{-\mathit{g}}logp(\mathit{g}\mid \text{rest})\}\text{and}{q}^{\ast }({\sigma }_{\mathit{g}}^2)\propto exp\left\{E_{-{\sigma }_{\mathit{g}}^2}logp({\sigma }_{\mathit{g}}^2\mid \text{rest})\right\}$$

where rest includes both the observed data and all parameters not currently under consideration.

Using the full conditional distribution $p(\mathit{g}\mid \text{rest})\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)$, the optimal density q^*(g) is

$$\begin{array}{l}{q}^{\ast }(\mathit{g})\propto exp\{E_{-\mathit{g}}logp(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)\}\\ \propto exp[-\frac{1}{2}{\text{E}}_{-\mathit{g}}\{{\mathit{g}}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{M}}^T{\mathit{C}}^T\mathit{CM}+\frac{1}{{\sigma }_{\mathit{g}}^2}{\mathit{D}}^{-1}\right)\mathit{g}-2\left(\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-{\mathit{b}}^T{\mathit{Z}}^T\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{CM}\right)\right)\mathit{g}\left\}\right]\\ \propto exp\left\{-\frac{1}{2}{\left(\mathit{g}-{\mathit{\mu }}_{q(\mathit{g})}\right)}^T{\mathbf{\sum }}_{q(\mathit{g})}^{-1}\left(\mathit{g}-{\mathit{\mu }}_{q(\mathit{g})}\right)\right\}\end{array}$$

where

$$\begin{array}{l}{\mathbf{\sum }}_{q(\mathit{g})}={\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+n{\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}+{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}{\mathit{D}}^{-1}\right\}}^{-1},\\ {\mathit{\mu }}_{q(\mathit{g})}={\mathbf{\sum }}_{q(\mathit{g})}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{z}}^T-{\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{Z}}^T)({\mu }_{q(\mathit{C})}\mathit{M})\right\}}^T.\end{array}$$ (3.2)

Thus the optimal density q^*(g) is N(μ_q(g), Σ_q(g)). Similarly, the optimal density $q^{\ast }({\sigma }_{\mathit{g}}^2)$ is

$$\begin{array}{l}{q}^{\ast }({\sigma }_{\mathit{g}}^2)\propto exp\{E_{-\mathit{g}}logp(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)p({\sigma }_{\mathit{g}}^2)\}\\ \propto {({\sigma }_{\mathit{g}}^2)}^{-A_{\mathit{g}}-K_g/2-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{g}}^2}{\text{E}}_{-{\sigma }_{\mathit{g}}^2}\left(B_{\mathit{g}}+\frac{1}{2}{\mathit{g}}^T{\mathit{D}}^{-1}\mathit{g}\right)\right\}.\end{array}$$

Thus $q^{\ast }({\sigma }_{\mathit{g}}^2)$ is $\text{IG}(A_{\mathit{g}}+K_g/2,B_{q({\sigma }_{\mathit{g}}^2)})$ where

$$B_{q({\sigma }_{\mathit{g}}^2)}=B_{\mathit{g}}+\frac{1}{2}\left({\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{D}}^{-1}{\mathit{\mu }}_{q(\mathit{g})}+\text{tr}({\mathit{D}}^{-1}{\mathbf{\sum }}_{q(\mathit{g})})\right)$$ (3.3)

Note that, when $q({\sigma }_{\mathit{g}}^2)=q^{\ast }({\sigma }_{\mathit{g}}^2)$, the term ${\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}$ appearing in (3.2) is equal to $\frac{A_{\mathit{g}}+K_g/2}{B_{q({\sigma }_{\mathit{g}}^2)}}$.

Thus, the optimal densities q^*(g) and $q^{\ast }({\sigma }_{\mathit{g}}^2)$ belong to parametric families with the parameters explicitly determined by the distributions of the remaining model parameters and the observed data. Similar derivations for the parameters of the remaining optimal densities are derived in Appendix A. Taken together, these solutions lead to Algorithm 1 for approximate Bayesian inference in the functional linear regression setting.

Algorithm 1.

Iterative scheme for obtaining the parameters in the optimal densities in the longitudinal functional regression model (2.8).

Initialize: $B_{q({\sigma }_{\mathit{g}}^2)}\dots B_{q({\sigma }_{\mathit{Y}}^2)}>0$, , μq(C) = 0, μq(g) = 0, μq(β) = 0, Σq(g) = I, Λq = I.

Cycle:

$$\begin{array}{l}{\mathbf{\sum }}_{q(\mathit{\beta })}\leftarrow {\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{z}}^T\mathit{z}+\frac{1}{{\sigma }_{\mathit{\beta }}^2}\mathit{I}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{\beta })}\leftarrow {\mathbf{\sum }}_{q(\mathit{\beta })}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{Z}}^T-{\mathit{\mu }}_{q(\mathit{g})}^T\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}^T\right)\mathit{z}\right\}}^T\\ {\mathbf{\sum }}_{q(\mathit{b})}\leftarrow {\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{Z}}^T\mathit{Z}+{\mu }_{q(1/{\sigma }_{\mathit{b}}^2)}\mathit{I}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{b})}\leftarrow {\mathbf{\sum }}_{q(\mathit{b})}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{z}}^T-{\mathit{\mu }}_{q(\mathit{g})}^T\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}^T\right)\mathit{Z}\right\}}^T\\ {\mathbf{\sum }}_{q(\mathit{C})}\leftarrow {\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\mathit{M}({\mathit{\mu }}_{q(\mathit{g})}{\mathit{\mu }}_{q(\mathit{g})}^T+{\mathbf{\sum }}_{q(\mathit{g})}){\mathit{M}}^T+{\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}{\mathit{\psi }}^T\mathit{\psi }+{\mathrm{\Lambda }}_q^{-1}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{C})}^T\leftarrow {\mathbf{\sum }}_{q(\mathit{C})}{({\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}Y{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T-{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mu }_{q(\mathit{\beta })}\mathit{z}{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\mathit{Z}{\mathit{\mu }}_{q(\mathit{b})}{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T+{\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}\mathit{W}\mathit{\psi })}^T\\ {\mathbf{\sum }}_{q(\mathit{g})}\leftarrow {\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+n{\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}+{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}{\mathit{D}}^{-1}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{g})}\leftarrow {\mathbf{\sum }}_{q(\mathit{g})}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{z}}^T-{\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{Z}}^T\right)({\mathit{\mu }}_{q(\mathit{C})}\mathit{M})\right\}}^T\\ B_{q({\lambda }_k)}\leftarrow B_{\lambda }+\frac{1}{2}\left({({\mathit{\mu }}_{q(\mathit{C})}^k)}^T({\mathit{\mu }}_{q(\mathit{C})}^k)+n{({\mathbf{\sum }}_{q(\mathit{C})})}_{kk}\right),1\le j\le K_x\\ B_{q({\sigma }_{\mathit{X}}^2)}\leftarrow B_{\mathit{X}}+\frac{1}{2}\left\{{\sum }_{i=1}^I{\sum }_{j=1}^J{\left|\right|{({\mathit{W}}_{ij}-{\mathit{\mu }}_{q(\mathit{c}),ij}{\mathit{\psi }}^T)}^T\left|\right|}^2+(nJ)\text{tr}({\mathit{\psi }}^T\mathit{\psi }{\mathbf{\sum }}_{q(\mathit{C})})\right\}\\ B_{q({\sigma }_{\mathit{b}}^2)}\leftarrow B_{\mathit{b}}+\frac{1}{2}\left({\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{\mu }}_{q(\mathit{b})}+\text{tr}({\mathbf{\sum }}_{q(\mathit{b})})\right)\\ B_{q({\sigma }_{\mathit{g}}^2)}\leftarrow B_{\mathit{g}}+\frac{1}{2}\left({\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{D}}^{-1}{\mathit{\mu }}_{q(\mathit{g})}+\text{tr}({\mathit{D}}^{-1}{\mathbf{\sum }}_{q(\mathit{g})})\right)\\ B_{q({\sigma }_{\mathit{Y}}^2)}\leftarrow B_{\mathit{Y}}+\frac{1}{2}[{\left|\right|\mathit{Y}-\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{Zb}-{\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\left|\right|}^2+\text{tr}({\mathit{z}}^T\mathit{z}{\mathbf{\sum }}_{q(\mathit{\beta })})\\ -{({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})})}^T({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})})\\ +{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\\ +\text{tr}\left\{{\mathit{M}}^T\left({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})}\right)\mathit{M}{\mathbf{\sum }}_{q(\mathit{g})}\right\}\\ +\text{tr}\left\{{\mathit{Z}}^T\mathit{Z}{\mathbf{\sum }}_{q(\mathit{b})}\right\}]\end{array}$$

until the increase in p(Y, W; q) is negligible.

Further, as shown in Appendix B, the q-specific lower bound on the marginal log-likelihood has the form

$$\begin{array}{l}log\underset{\_}{p}(\mathit{Y},\mathit{W};q)=\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{\beta })}\mid }{{\sigma }_{\beta }^{2p}}\right)-\frac{1}{2{\sigma }_{\mathit{\beta }}^2}\left\{{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{\mu }}_{q(\mathit{\beta })}+\text{tr}({\mathbf{\sum }}_{q(\mathit{\beta })})\right\}\\ +\frac{1}{2}{\text{E}}_{q^{\ast }}[log(\mid {\mathbf{\sum }}_{q(\mathit{g})}\mid )]+\sum _{k=1}^{K_x}\frac{nJ}{2}log({({\mathbf{\sum }}_{q(\mathit{C})})}_{kk})\\ +\frac{1}{2}{\text{E}}_{q^{\ast }}[log(\mid {\mathbf{\sum }}_{q(\mathit{b})}\mid )]-\left(A_{\mathit{g}}+\frac{K_g}{2}\right)log\left(B_{q({\sigma }_{\mathit{g}}^2)}\right)\\ -\left(A_{\mathit{b}}+\frac{n}{2}\right)log\left(B_{q({\sigma }_{\mathit{b}}^2)}\right)-\left(A_{\mathit{Y}}+\frac{nJ}{2}\right)log\left(B_{q({\sigma }_{\mathit{Y}}^2)}\right)\\ -\left(A_{\mathit{X}}+\frac{\mathit{nJN}}{2}\right)log\left(B_{q({\sigma }_{\mathit{X}}^2)}\right)\\ -\sum _{k=\text{1}}^{K_x}\left\{\left(A_{\lambda }+\frac{nJ}{2}\right)log\left(B_{q({\lambda }_k)}\right)\right\}+\text{const}.\end{array}$$

where const. is an additive constant that remains unchanged in the iterations of Algorithm 1. All parameters denoted A and B and indexed by a subscript are hyperparameters of the inverse gamma prior distributions of the variance components. The quantity log p(Y, W; q) is typically monitored for convergence in place of p(Y, W; q). Note that, because several substitutions are made to simplify the expression, this form for log p(Y, W; q) is only valid at the end of each iteration of Algorithm 1, and only if the parameters are updated in the order given.

Finally, posterior credible intervals are readily obtained for all model parameters. However, variational approximations in effect fit a parametric distribution to a mode of the posterior density, which may have consequences when the posterior is multi-modal or more diffuse than the approximating parametric distribution; in such cases one could expect that credible intervals from variational Bayes and MCMC sampling may not agree. This was not a problem in our simulations, where the agreement between the approximate and MCMC-sampled posterior distribution is high, although in our application the variational credible intervals are slightly narrower than those from MCMC sampling.

4. Simulations

In this section we undertake simulation exercises with two goals. First, we evaluate our approach’s overall ability to accurately estimate all coefficients in a functional regression model. Second, we compare the individual approximate posterior distributions q^*(θ_l) ≈ p(θ_l | rest) to those given by Markovchain Monte Carlo (MCMC) sampling in order to examine the quality of the variational approximation in the functional regression setting. We conduct separate simulations for the cross-sectional and longitudinal situations. The MCMC sampling was executed in WinBUGS and the variational Bayes approach was implemented in R.

4.1. Cross-sectional functional regression

We generate samples from the model

$$\begin{array}{l}{Y}_i={\beta }_1+z_i{\beta }_2+{\int }_0^1{X}_i^S(t)\gamma (t)dt+{\epsilon }_i^Y\\ {\epsilon }_i^Y\sim \text{N}(0,{\sigma }_Y^2).\end{array}$$ (4.1)

Here we assume I = {100, 500} subjects and generate z_i ~ Unif [−5, 5]. We take ${\sigma }_Y^2=5,{\beta }_1={\int }_0^1\mu (t)\gamma (t)dt=3.47$, β₂ = 3, and γ(t) = cos(2πt).

To generate our simulated functional predictors $X_i^S(t)$, we use the functional predictors $X_i^A(t)$ from our scientific application in the following way. First, we compute a functional principal components decomposition of the $X_i^A(t)$ with eigenfunctions ψ₁(t), ψ₂(t), … and corresponding eigenvalues λ₁, λ₂, …. Recall that the application predictors can be approximated using $X_i^A(s)=\mu (t)+{\sum }_{k=1}^{K_x}{c}_{ik}{\psi }_k(t)$ where μ(t) is a population mean function, K_x is the truncation lag and the c_ik are uncorrelated random variables with variance λ_k. Using this, we construct simulated regressors

$$\begin{array}{l}{X}_i^S(t)=\mu (t)+\sum _{k=1}^{K_x}{c}_{ik}{\psi }_k(t)+{\epsilon }_i^X(t)\\ {\mathit{c}}_i\sim \text{N}(\mathbf{0},\text{diag}({\lambda }_1,\dots ,{\lambda }_{K_x}));{\epsilon }_i^X(t)\sim \text{N}(0,{\sigma }_X^2).\end{array}$$

This parametric construction of the simulated functional predictors is related to the application predictors through the mean function μ(t), the eigenfunctions ψ_k(t), and the variance components λ_k. As in our application, the simulated predictors are observed on a grid of length 93.

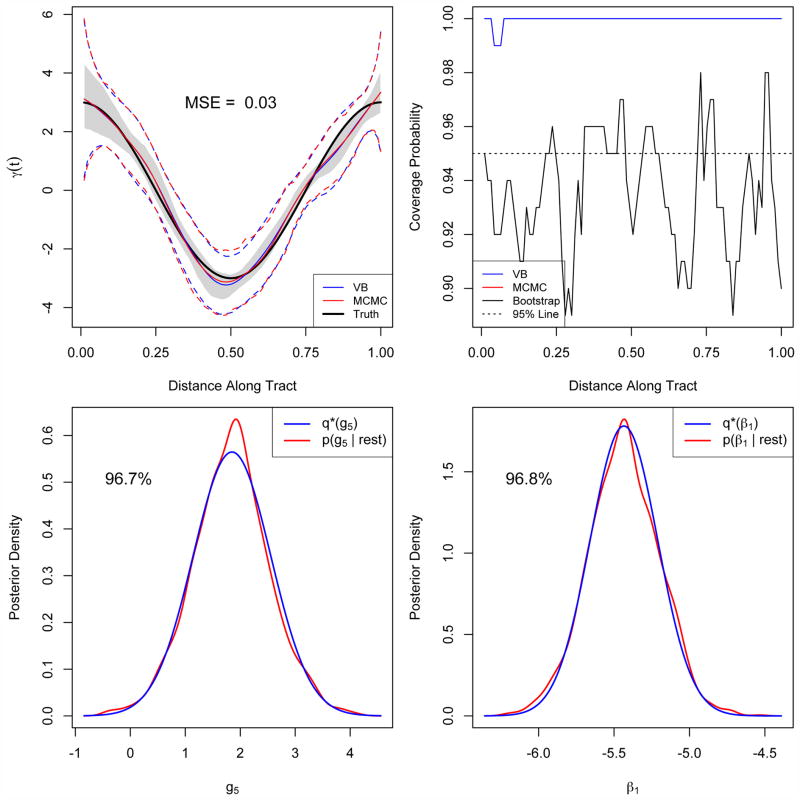
We generate 100 such datasets for I = 100 and I = 500 and fit model (4.1) using both MCMC simulation and the variational approximation approach. For the MCMC simulation, we use chains of length 2500 with the first 1000 as burn-in. Representative examples of the MCMC model fits were inspected using trace and autocorrelation plots to ensure that the posterior samples were reasonable and that the comparison with variational Bayes was fair. To evaluate the ability of the proposed approach to estimate the functional coefficient γ(t) we use the mean squared error (MSE) ${\int }_0^1{(\widehat{\gamma }(t)-\gamma (t))}^{2}dt$. A comparison of MSEs for the variational approach with the more computationally intensive MCMC sampling is given in table 1. To provide context for this table, in the left panel of Figure 3 we plot the estimated coefficient function resulting in the median MSE for I = 100.

Table 1.

Average integrated MSE for γ(t) and average MSE for the non-functional covariates β₁, β₂ estimated using the variational approximation, taken over 100 simulated datasets. For I = 500, large outlier for the MCMC MSE were removed in the calculation of the average

		γ(t)	β1	β2
I = 100	VB	.050	.071	.051
	MCMC	.054	.071	.051
I = 500	VB	.046	.008	.001
	MCMC	.120	.008	.001

Fig 3.

The top left panel shows the estimated coefficient function corresponding to the median MSE = 0.049, as well as variational and MCMC 95% credible intervals (dashed lines) and the 95% bootstrap interval (shaded region). The top-right panel displays the coverage probabilities of the credible intervals over the domain of the predictor (note there is perfect overlap of the VB and MCMC coverage probabilities). The bottom panels show posterior densities estimated by variational approximations and by MCMC sampling from the same simulated dataset (shown in dashed and solid lines, respectively), and provide the accuracy of the approximation expressed as a percent.

Interestingly, when I = 500 the MSEs for MCMC sampling contain several large outliers, which raises the average MSE for the coefficient function in Table 1. Upon inspection, it was found that these large values corresponded to model fits in which the chains for g were bimodal. A large primary mode surrounded the true parameter value but a smaller, more diffuse mode corresponded to a model overfit. We refit these models using as initial parameter values the estimates provided by the variational approach, which caused the bimodal behavior to disappear and brought the MSEs (and average MSE) down to levels similar to the remaining model fits.

We also quantify the quality of the variational approximation to the MCMC-sampled posterior by computing the accuracy for each parameter in the model using $\text{Accuracy}=1-\frac{\mid p({\theta }_l\mid \text{rest})-q^{\ast }({\theta }_l)\mid }{2}\in [0,1]$; scores near 1 indicate a high 2 level of agreement between the two densities. Due to the large number of parameters in the model, we present only a subset of the average accuracies in Table 2. As with the MSE, context for this table in given in Figure 3. The accuracy of g is affected by the presence of outliers, attributable to the same bimodal MCMC samples that caused the very large MSEs appearing in Table 1.

Table 2.

The accuracy of the variational approximation to the MCMC-sampled posterior, expressed as a percentage, for a subset of parameters in the cross-sectional functional regression model (2.5)

Accuracy	g5	g20	c1,1	c1,10	λ1,1	λ1,10	${\sigma }_{\mathit{Y}}^2$
I = 100	96.3	95.1	98.3	98.0	96.9	97.2	95.0
I = 500	86.7	82.6	97.6	97.8	97.6	88.3	96.3

Due to the substantial decrease in computation time using variational Bayes over MCMC methods, we are able to construct 95% bootstrap confidence intervals by sampling subjects with replacement and refitting model (4.1) using the variational approach. While credible intervals provided by MCMC or by a single variational fit are overly conservative, the bootstrap intervals are on average .46 times narrower and, averaged over the domain, have coverage probability 93.4% for I = 100 and 93.6% for I = 500. The far right panel of Figure 3 displays the coverage probabilities of the various credible and confidence intervals for I = 500.

As demonstrated in Table 2 and Figure 3, the variational approximation performs well in this functional regression setting, both in terms of low MSEs and of agreement the with MCMC-sample posterior density. This stems from the low posterior dependence between the parameters, which is assumed in the use of the density transform approach. Additionally, the use of the bootstrap allows the construction of confidence intervals that are not overly conservative.

Importantly, even in this simulation the computational burden is greatly reduced through the use of variational approximations. For I = 100, the MCMC sampling took on average 315 seconds, while the approximation was computed in on average 0.04 seconds (Dual Core 3.06GHz Processor; 4 GB RAM; OS X 10.6.4). For I = 500, the respective times were 1614 and 0.2 seconds. Constructing the bootstrap confidence intervals, based on 400 bootstrap samples, took on average an additional 20 and 76 seconds for I = 100 and I = 500, respectively.

4.2. Longitudinal functional regression

Next, we generate samples from the model

$$\begin{array}{l}{Y}_{ij}={\beta }_1+z_{ij}{\beta }_2+{\mathit{b}}_i+{\int }_0^1{X}_{ij}^S(t)\gamma (t)dt+{\epsilon }_{ij}^Y\\ {\epsilon }_{ij}^Y\sim \text{N}(0,{\sigma }_Y^2).\end{array}$$ (4.2)

We take I = 100 subjects with J = 3 visits per subject; random effects b are $\text{N}(0,{\sigma }_{\mathit{b}}^2)$ with ${\sigma }_{\mathit{b}}^2=5$. Again, we generate z_i ~ Unif [−5, 5], take ${\sigma }_Y^2=5,{\beta }_1={\int }_0^1\mu (t)\gamma (t)dt=12.68$, β₂ = 3, and select γ(t) = cos(2πt). The functional predictors $X_{ij}^S(t)$ are constructed as above; we take c_ij ~ N (0, diag(λ₁, …, λ_ijKx)) so that the PC loadings are not correlated within subjects.

We fit model (2.8) for 100 simulated datasets. As in the cross-sectional case, we use chain lengths of 2500, with 1000 as burn-in, for the MCMC sampling. In Table 3 we display the average MSE of the estimated functional and scalar parameters and the subject-specific random effects. Again, the variational approximation performs as well as the MCMC sampling with a substantial difference in computation time: the MCMC sampling took on average 973 seconds, while the approximation was calculated in on average .2 seconds.

Table 3.

Average integrated MSE for γ(t) and average MSE for the non-functional covariates β₁, β₂ estimated using the variational approximation, taken over 100 simulated datasets

		γ(t)	β1	β2
I = 100, J = 3	VB	.026	.0003	.0002
	MCMC	.030	.0002	.0002

5. Application

In our scientific application, we analyze the association between measures of intracranial white matter and cognitive decline in multiple sclerosis patients. White matter is made up of myelinated axons, the long fibers used to transmit electrical signals in the brain, and is organized into bundles, or tracts. Major examples of white matter tracts are the corpus callosum, the corticospinal tracts, and the optic radiations. Here we focus on the corpus callosum, a collection of white-matter fibers which connects the two hemispheres of the brain.

Myelin, the fatty insulation surrounding white matter fibers, allows electrical signals to be propagated at high speeds along white matter tracts. Multiple sclerosis is a demyelinating autoimmune disease that causes in lesions in the white matter. These lesions disrupt electrical signals, and, over time, result in severe disability in affected patients. To measure cognitive disability, we use the Paced Auditory Serial Addition Test (PASAT), which assesses auditory processing speed and calculation ability. In this test, a proctor reads aloud a sequence of 60 numbers at three-second intervals, while the subject provides the sum of the previous two numbers spoken. This test has scores between 0 and 60 indicating the number of correct sums provided by the subject; the score 60 indicates the highest level of cognitive ability [8].

To quantify white matter, we use diffusion tensor imaging, a magnetic resonance imaging that measures the diffusivity of water in the brain. Because white matter is organized in bundles, water tends to diffuse anisotropically along the tract, which makes their reconstruction from MRI possible. By measuring diffusivity along several gradients, diffusion tensor imaging is able to produce detailed images of intracranial white matter [1, 2, 14, 17]. Moreover, continuous summaries of individual white matter tracts, parameterized by distance along the tract and called tract profiles, can be constructed from diffusion tensor images. Here we study the fractional anisotropy tract profile of the right corticospinal tract; this gives a measure of how anisotropic diffusion is along the tract.

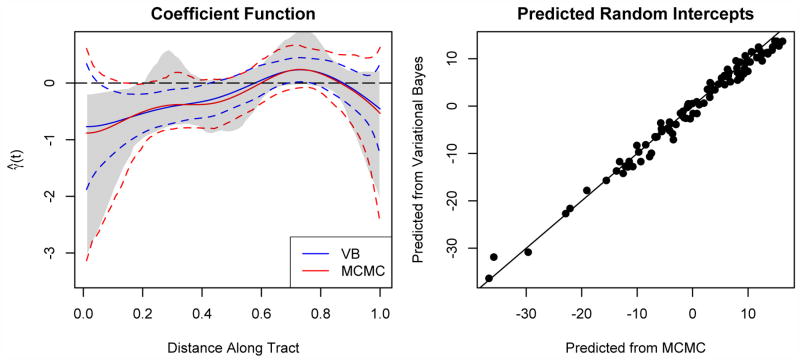
Our study consists of 100 multiple sclerosis patients with between two and eight visits each; a total of 334 visits were observed. Study participants had ages between 21 and 71 years, and 63% were women. We fit model (2.8), using age and gender as non-functional covariates and the mean diffusivity tract profile of the corpus callosum as a functional predictor. We include subject-specific random intercepts to account for the repeated observations at the subject level. The model was fit using both the variational approximation and MCMC sampling; the results are shown in Figure 4.

Fig 4.

Results of fitting model (2.8) to the diffusion tensor imaging dataset. The left panel shows the estimated coefficient function; credible intervals for both methods are shown in dashed lines, and the nonparametrically bootstrapped interval shown in grey; the right panel shows the random intercepts predicted by both variational Bayes and MCMC sampling.

Previous studies have linked damage in the corpus callosum to cognitive decline as measured by PASAT and other tests [15, 20]. However, these studies lacked the spatial information present in the functional treatment here, which proves to be important. From the estimated coefficient function and bootstrapped confidence intervals, we see that the region from roughly 0 to .2 is negatively associated with the PASAT outcome – that is, subjects with above-average mean diffusivity in these regions tend to have lower PASAT scores. A second region, from .65 to .8, is positively associated with the outcome. We base inference on the bootstrapped intervals due to the overly conservative coverage of the MCMC and variational Bayes credible intervals; however, there is broad agreement between all intervals regarding the location of regions of interest. Note the interpretation of the coefficient function is marginal, rather than conditional on a subject’s random intercept. The random intercepts are an important component of the model: a model including only random intercepts explains roughly 80% of the outcome variability, while adding functional and nonfunctional covariates raises this to 89%. Finally, age and gender were not found to be statistically significant, but were retained as scientifically important covariates. Their inclusion did not meaningfully affect the shape or significance of the functional predictor.

There is broad agreement between the variational Bayes and MCMC model fits: the point estimates of the coefficient and the random intercepts are very similar, and the credible intervals indicate the same regions of significance. On the other hand, the credible interval using MCMC is wider than that using variational Bayes. As noted above, the variational method can result in narrower confidence intervals if the approximating density is less diffuse than the MCMC-sampled posterior which appears to be the case here. In this application, we posit that the lesser importance of the functional predictors in comparison to the random intercepts leads to increased posterior variability in the estimated functional coefficient. Indeed, when we fit a model without the random subject-specific intercept the confidence intervals for Bayesian and variational Bayesian approximations became indistinguishable.

Also shown in Figure 4 as a grey band is the 95% bootstrap confidence interval, constructed by nonparametrically resampling subjects and fitting the longitudinal functional regression model using variational Bayes. Inference for the coefficient function is largely unchanged based on the bootstrap interval except in the region from .2 to .4, which does not appear to be significantly associated with the outcome. Although the credible intervals using variational Bayes are likely too narrow, the computational gain and accurate point estimates provided by this method allow for the construction of bootstrap confidence intervals, which performed much better in our simulations.

6. Discussion

The variational Bayes approach to functional regression was motivated by a pressing need for computationally feasible Bayesian inference in a large-data setting. We have developed iterative algorithms for approximate inference in both the cross-sectional and longitudinal regression settings, and analyzed a longitudinal neuroimaging study. The methods developed: 1) flexibly estimate all parameters in the cross-sectional and longitudinal functional regression models; 2) accurately approximate the posterior distributions of all model parameters; 3) retain the advantages of Bayesian inference, including the ability to jointly model the functional predictors and scalar outcomes and easily constructed credible bands; 4) require orders of magnitude less computational effort than MCMC techniques; and 5) allow the construction of nonparametric bootstrap confidence intervals, which seem to have good coverage probabilities.

A few limitations of the variational Bayes method are apparent. While our simulations indicate that variational techniques can be used with confidence in the functional regression setting, the approximation cannot be made more accurate by increasing computation time. Additionally, the iterative algorithms are based on involved algebraic derivations; those needed for functional regression have been carried out here, but additional work may be needed to adapt these algorithms to specific scientific settings. Lastly, the performance of credible intervals approximated using variational Bayes may not be satisfactory if the posterior distribution is multimodal or more diffuse than the approximating distribution, although the use of the nonparametric bootstrap can alleviate this issue.

Future work may proceed in several directions. The adaptation of the approach to non-Gaussian outcomes will expand the class of applications in which variational Bayes may be used for functional regression. Very large gains in computation time may be found in functional magnetic resonance imaging or other studies where the predictors are sampled at thousands or tens of thousands of points. More generally, variational Bayes has potential applications in several functional data analysis topics, including function-on-function regression and the decomposition of populations of functions.

Appendix A: Derivations

In this appendix we derive the optimal densities q^* for approximate Bayesian inference in the longitudinal functional regression model. For the cross-sectional case, one may omit the random effects b. We recall that, given a partition {θ₁, …, θ_L} of the parameter space θ, the explicit solution for q(θ_l), 1 ≤ l ≤ L, has the form

$$q_l^{\ast }({\mathit{\theta }}_l)\propto exp\{E_{{\mathit{\theta }}_{-l}}logp({\mathit{\theta }}_l\mid \text{rest})\};1\le l\le L$$ (A.1)

where rest ≡ {y, θ₁, …, θ_l−1, θ_l+1, …, θ_L}

A.1. Optimal densities for g and ${\sigma }_{\mathit{g}}^2$

Recall that $\mathit{g}\sim \text{N}(0,{\sigma }_{\mathit{g}}^2\mathit{D})$ and ${\sigma }_{\mathit{g}}^2\sim \text{IG}(A_{\mathit{g}},B_{\mathit{g}})$. According to (A.1), the optimal densities are given by

$$q^{\ast }(\mathit{g})\propto exp\{E_{-\mathit{g}}logp(\mathit{g}\mid \text{rest})\}\text{and}{q}^{\ast }({\sigma }_{\mathit{g}}^2)\propto exp\left\{E_{-{\sigma }_{\mathit{g}}^2}logp({\sigma }_{\mathit{g}}^2\mid \text{rest})\right\}.$$

The full conditional distribution p(g|rest) appearing above is given by

$$\begin{array}{l}p(\mathit{g}\mid \text{rest})\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)\\ \propto exp\left[-\frac{1}{2}\left\{\frac{1}{{\sigma }_{\mathit{Y}}^2}{\left(\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\right)}^T\left(\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\right)+\frac{1}{{\sigma }_{\mathit{g}}^2}{\mathit{g}}^T{\mathit{D}}^{-1}\mathit{g}\right\}\right]\\ \propto exp[-\frac{1}{2}\{{\mathit{g}}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{M}}^T{\mathit{C}}^T\mathit{CM}+\frac{1}{{\sigma }_{\mathit{g}}^2}{\mathit{D}}^{-1}\right)\mathit{g}\\ -2\left(\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-\mathit{Zb}\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{CM}\right)\right)\mathit{g}\left\}\right].\end{array}$$

Therefore the optimal density q^*(g) is

$$\begin{array}{l}{q}^{\ast }(\mathit{g})\propto exp[-\frac{1}{2}{\text{E}}_{-\mathit{g}}\{{\mathit{g}}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{M}}^T{\mathit{C}}^T\mathit{CM}+\frac{1}{{\sigma }_{\mathit{g}}^2}{\mathit{D}}^{-1}\right)\mathit{g}-2\left(\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-{\mathit{b}}^T{\mathit{Z}}^T\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{CM}\right)\right)\mathit{g}\left\}\right]\\ \propto exp\left\{-\frac{1}{2}{\left(\mathit{g}-{\mathit{\mu }}_{q(\mathit{g})}\right)}^T{\mathbf{\sum }}_{q(\mathit{g})}^{-1}\left(\mathit{g}-{\mathit{\mu }}_{q(\mathit{g})}\right)\right\}\end{array}$$

where

$$\begin{array}{l}{\mathbf{\sum }}_{q(\mathit{g})}={\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+n{\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}+{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}{\mathit{D}}^{-1}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{g})}={\mathbf{\sum }}_{q(\mathit{g})}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{z}}^T-{\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{Z}}^T\right)\left({\mathit{\mu }}_{q(\mathit{C})}\mathit{M}\right)\right\}}^T.\end{array}$$ (A.2)

Thus the optimal density q^*(g) is N(μ_q(g), Σ_q(g)).

Further, the full conditional $p({\sigma }_{\mathit{g}}^2\mid \text{rest})$ is given by

$$\begin{array}{l}p({\sigma }_{\mathit{g}}^2\mid \text{rest})\propto p(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)p({\sigma }_{\mathit{g}}^2)\\ \propto {({\sigma }_{\mathit{g}}^2)}^{-K_g/2}exp\left\{-\frac{1}{2{\sigma }_{\mathit{g}}^2}{\mathit{g}}^T{\mathit{D}}^{-1}\mathit{g}\right\}\times {({\sigma }_{\mathit{g}}^2)}^{-A_{\mathit{g}}-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{g}}^2}{B}_{\mathit{g}}\right\}\\ ={({\sigma }_{\mathit{g}}^2)}^{-A_{\mathit{g}}-K_g/2-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{g}}^2}\left(B_{\mathit{g}}+\frac{1}{2}{\mathit{g}}^T{\mathit{D}}^{-1}\mathit{g}\right)\right\}\end{array}$$

so that the optimal density $q^{\ast }({\sigma }_{\mathit{g}}^2)$ is

$$q^{\ast }({\sigma }_{\mathit{g}}^2)\propto exp\left\{-(A_{\mathit{g}}+K_g/2+1)log({\sigma }_{\mathit{g}}^2)-\frac{1}{{\sigma }_{\mathit{g}}^2}{\text{E}}_{-{\sigma }_{\mathit{g}}^2}\left(B_{\mathit{g}}+\frac{1}{2}{\mathit{g}}^T{\mathit{D}}^{-1}\mathit{g}\right)\right\}.$$

Thus $q^{\ast }({\sigma }_{\mathit{g}}^2)$is $\text{IG}\left(A_{\mathit{g}}+K_g/2,B_{q({\sigma }_{\mathit{g}}^2)}\right)$ where

$$B_{q({\sigma }_{\mathit{g}}^2)}=B_{\mathit{g}}+\frac{1}{2}\left({\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{D}}^{-1}{\mathit{\mu }}_{q(\mathit{g})}+\text{tr}({\mathit{D}}^{-1}{\mathbf{\sum }}_{q(\mathit{g})})\right)$$ (A.3)

Note that, when $q({\sigma }_{\mathit{g}}^2)=q^{\ast }({\sigma }_{\mathit{g}}^2)$, the term ${\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}$ appearing in (A.2) is equal to $\frac{A_{\mathit{g}}+K_g/2}{B_{q({\sigma }_{\mathit{g}}^2)}}$.

A.2. Optimal densities for b and ${\sigma }_{\mathit{b}}^2$

Recall that $\mathit{b}\sim \text{N}(0,{\sigma }_{\mathit{b}}^2\mathit{I})$ and ${\sigma }_{\mathit{b}}^2\sim \text{IG}(A_{\mathit{b}},B_{\mathit{b}})$.

The full conditional distribution p(b|rest) is given by

$$\begin{array}{l}p(\mathit{b}\mid \text{rest})\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p(\mathit{b}\mid {\sigma }_{\mathit{b}}^2)\\ \propto exp\left[-\frac{1}{2}\left\{\frac{1}{{\sigma }_{\mathit{Y}}^2}{(\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg})}^T(\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg})+\frac{1}{{\sigma }_{\mathit{b}}^2}{\mathit{b}}^T{\mathit{I}}^{-1}\mathit{b}\right\}\right]\\ \propto exp\left[-\frac{1}{2}\left\{{\mathit{b}}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{Z}}^T\mathit{Z}+\frac{1}{{\sigma }_{\mathit{b}}^2}\mathit{I}\right)\mathit{b}-2\left(\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-{\mathit{g}}^T{\mathit{M}}^T{\mathit{C}}^T\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{Z}\right)\right)\mathit{b}\right\}\right]\end{array}$$

Therefore, by (A.1), the optimal density q^*(b) is

$$q^{\ast }(\mathit{b})\propto exp[-\frac{1}{2}{\text{E}}_{-\mathit{b}}\{{\mathit{b}}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{Z}}^T\mathit{Z}+\frac{1}{{\sigma }_{\mathit{b}}^2}\mathit{I}\right)\mathit{b}-2\left(\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-{\mathit{g}}^T{\mathit{M}}^T{\mathit{C}}^T\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{Z}\right)\right)\mathit{b}\left\}\right].$$

After taking the expectation above, the optimal density q^*(b) is N(μ_q(b), Σ_q(b)) where

$$\begin{array}{l}{\mathbf{\sum }}_{q(\mathit{b})}={\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{Z}}^T\mathit{Z}+{\mu }_{q(1/{\sigma }_{\mathit{b}}^2)}\mathit{I}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{b})}={\mathbf{\sum }}_{q(\mathit{b})}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{z}}^T-{\mathit{\mu }}_{q(\mathit{g})}^T\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}^T\right)\mathit{Z}\right\}}^T.\end{array}$$ (A.4)

Further, the full conditional $p({\sigma }_{\mathit{b}}^2\mid \text{rest})$ is given by

$$\begin{array}{l}p({\sigma }_{\mathit{b}}^2\mid \text{rest})\propto p(\mathit{b}\mid {\sigma }_{\mathit{b}}^2)p({\sigma }_{\mathit{b}}^2)\\ \propto {({\sigma }_{\mathit{b}}^2)}^{-n/2}exp\left\{-\frac{1}{2{\sigma }_{\mathit{b}}^2}{\mathit{b}}^T\mathit{b}\right\}\times {({\sigma }_{\mathit{b}}^2)}^{-A_{\mathit{b}}-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{g}}^2}{B}_{\mathit{b}}\right\}\\ ={({\sigma }_{\mathit{b}}^2)}^{-A_{\mathit{b}}-n/2-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{b}}^2}\left(B_{\mathit{b}}+\frac{1}{2}{\mathit{b}}^T\mathit{b}\right)\right\}\end{array}$$

so that the optimal density $q^{\ast }({\sigma }_{\mathit{b}}^2)$ is

$$q^{\ast }({\sigma }_{\mathit{b}}^2)\propto exp\left\{-(A_{\mathit{b}}+n/2+1)log({\sigma }_{\mathit{b}}^2)-\frac{1}{{\sigma }_{\mathit{b}}^2}{\text{E}}_{-{\sigma }_{\mathit{b}}^2}\left(B_{\mathit{b}}+\frac{1}{2}{\mathit{b}}^T\mathit{b}\right)\right\}.$$

Thus $q^{\ast }({\sigma }_{\mathit{b}}^2)$ is $\text{IG}(A_b+n/2,B_{q({\sigma }_{\mathit{b}}^2)})$ where

$$B_{q({\sigma }_{\mathit{b}}^2)}=B_{\mathit{b}}+\frac{1}{2}\left({\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{\mu }}_{q(\mathit{b})}+\text{tr}\text{(}{\mathbf{\sum }}_{q(\mathit{b})}\text{)}\right)$$ (A.5)

Note that, when $q({\sigma }_{\mathit{b}}^2)=q^{\ast }({\sigma }_{\mathit{b}}^2)$, the term ${\mu }_{q(1/{\sigma }_{\mathit{b}}^2)}$ appearing in (A.4) is equal to $\frac{A_{\mathit{b}}+n/2}{B_{q({\sigma }_{\mathit{b}}^2)}}$.

A.3. Optimal densities for C and λ_j

Recall that c_ij ~ N (0, Λ), where Λ = diag(λ₁, …, λ_Kx) and λ_k ~ IG (A_λ, B_λ) for 1 ≤ k ≤ K_x. In the following, we continue to use c_ij as the PC loadings for subject i at visit j and C as the matrix constructed by row-stacking the c_ij. We additionally use μ_q(c),ij as the expected value of c_ij with respect to the q(C) distribution and μ_q(C) as the matrix constructed by row-stacking the μ_q(c),ij. Finally, let ${\mathrm{\Lambda }}_q^{-1}=\text{diag}({\mu }_{q(1/{\lambda }_1)},\dots ,{\mu }_{q(1/{\lambda }_k)})$

The full conditional distribution p(C|rest) is given by

$$\begin{array}{l}p(\mathit{C}\mid \text{rest})\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p(\mathit{W}\mid \mathit{C},{\sigma }_{\mathit{X}}^2)p(C\mid \mathrm{\Lambda })\\ \propto exp\left[-\frac{1}{2}\text{tr}\left\{\frac{1}{{\sigma }_{\mathit{Y}}^2}{\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-{\mathit{b}}^T{\mathit{Z}}^T-{\mathit{g}}^T{\mathit{M}}^T{\mathit{C}}^T\right)}^T\left({\mathit{Y}}^T-{\mathit{\beta }}^T{\mathit{z}}^T-{\mathit{b}}^T{\mathit{Z}}^T-{\mathit{g}}^T{\mathit{M}}^T{\mathit{C}}^T\right)\right\}\right]\times exp\left[-\frac{1}{2}\text{tr}\left\{\frac{1}{{\sigma }_{\mathit{X}}^2}{\left({\mathit{W}}^T-\mathit{\psi }{\mathit{C}}^T\right)}^T\left({\mathit{W}}^T-\mathit{\psi }{\mathit{C}}^T\right)\right\}\right]\times exp\left\{-\frac{1}{2}\text{tr}(\mathit{C}{\mathrm{\Lambda }}^{-1}{\mathit{C}}^T)\right\}\\ \propto exp[-\frac{1}{2}\text{tr}\{\mathit{C}\left(\frac{{\mathit{Mg}\mathit{g}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}+\frac{{\mathit{\psi }}^T\mathit{\psi }}{{\sigma }_{\mathit{X}}^2}+{\mathrm{\Lambda }}^{-1}\right){\mathit{C}}^T-2\left(\frac{{\mathit{Yg}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}-\frac{\mathit{z}\mathit{\beta }{\mathit{g}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}-\frac{\mathit{Zb}{\mathit{g}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}+\frac{\mathit{W}\mathit{\psi }}{{\sigma }_{\mathit{X}}^2}\right){\mathit{C}}^T\}]\end{array}$$

Therefore, by (A.1), the optimal density q^*(C) is

$$\begin{array}{l}{q}^{\ast }(\mathit{C})\propto exp[-\frac{1}{2}{\text{E}}_{-\mathit{C}}\left[\text{tr}\right\{\mathit{C}\left(\frac{{\mathit{Mgg}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}+\frac{{\mathit{\psi }}^T\mathit{\psi }}{{\sigma }_{\mathit{X}}^2}+{\mathrm{\Lambda }}^{-1}\right){\mathit{C}}^T-2\left(\frac{{\mathit{Yg}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}-\frac{\mathit{z}\mathit{\beta }{\mathit{g}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}-\frac{\mathit{Zb}{\mathit{g}}^T{\mathit{M}}^T}{{\sigma }_{\mathit{Y}}^2}+\frac{\mathit{W}\mathit{\psi }}{{\sigma }_{\mathit{X}}^2}\right){\mathit{C}}^T\}\left]\right]\\ \propto exp\left\{-\frac{1}{2}\left[\sum _{i=1}^I\sum _{j=1}^J{\left\{{({\mathit{c}}_{ij})}^T-{({\mathit{\mu }}_{q(\mathit{c}),ij})}^T\right\}}^T{\mathbf{\sum }}_{q(\mathit{C})}^T\left\{{({\mathit{c}}_{ij})}^T-{({\mathit{\mu }}_{q(\mathit{c}),ij})}^T\right\}\right]\right\}\end{array}$$

where

$$\begin{array}{l}{\mathbf{\sum }}_{q(\mathit{C})}={\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\mathit{M}({\mathit{\mu }}_{q(\mathit{g})}{\mathit{\mu }}_{q(\mathit{g})}^T+{\mathbf{\sum }}_{q(\mathit{g})}){\mathit{M}}^T+{\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}{\mathit{\psi }}^T\mathit{\psi }+{\mathrm{\Lambda }}_q^{-1}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{C})}^T={\mathbf{\sum }}_{q(\mathit{C})}{({\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}Y{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T-{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{\mu }}_{q(\mathit{\beta })}\mathit{z}{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T-{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\mathit{Z}{\mathit{\mu }}_{q(\mathit{b})}{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T+{\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}\mathit{W}\mathit{\psi })}^T.\end{array}$$ (A.6)

Thus the optimal density q^*(C) is a product of Normally distributed random vectors sharing a common covariance matrix and with means the rows of μ_q(C).

In the derivation of the optimal density q^*(λ_k), 1 ≤ k ≤ K_x, we let C^k denote the k^th column of C and ${\mathit{\mu }}_{q(\mathit{C})}^k$ denote the k^th column of μ_q(C). Further, we let (Σ_q(C))_kk denote the (k, k)^th element of Σ_q(C). The full conditional p(λ_k|rest) is given by

$$\begin{array}{l}p({\lambda }_k\mid \text{rest})\propto p({\mathit{C}}^k\mid {\lambda }_k)p({\lambda }_k)\\ \propto {({\lambda }_k)}^{-(nJ)/2}exp\left\{-\frac{1}{2{\lambda }_k}{({\mathit{C}}^k)}^T({\mathit{C}}^k)\right\}\times {({\lambda }_k)}^{-A_{\lambda }-1}exp\left\{-\frac{1}{{\lambda }_k}{B}_{\lambda }\right\}\\ ={({\lambda }_k)}^{-A_{\lambda }-(nJ)/2-1}exp\left\{-\frac{1}{{\lambda }_k}\left(B_{\lambda }+\frac{1}{2}{({\mathit{C}}^k)}^T({\mathit{C}}^k)\right)\right\}\end{array}$$

so that the optimal density q^*(λ_k) is

$$q^{\ast }({\lambda }_k)\propto exp\left\{-(A_{\lambda }+(nJ)/2+1)log({\lambda }_k)-\frac{1}{{\lambda }_k}{\text{E}}_{-{\lambda }_k}\left(B_{\lambda }+\frac{1}{2}{({\mathit{C}}^k)}^T({\mathit{C}}^k)\right)\right\}.$$

Thus q^*(λ_k) is IG(A_λ + (nJ)/2, B_q(λk) where

$$B_{q({\lambda }_k)}=B_{\lambda }+\frac{1}{2}\left({({\mathit{\mu }}_{q(\mathit{C})}^k)}^T({\mathit{\mu }}_{q(\mathit{C})}^k)+n{({\mathbf{\sum }}_{q(\mathit{C})})}_{kk}\right)$$ (A.7)

Note that, when q(λ_k) = q*(λ_k), the term (k, k)^th entry of ${\mathrm{\Lambda }}_q^{-1}$ appearing in (A.6) is equal to $\frac{A_{\lambda }+(nJ)/2}{B_{q({\lambda }_k)}}$.

A.4. Optimal density for β

Recall that $\mathit{\beta }\sim \text{N}(0,{\sigma }_{\mathit{\beta }}^2\mathit{I})$.

The full conditional distribution p(β|rest) is given by

$$\begin{array}{l}p(\mathit{\beta }\mid \text{rest})\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p(\mathit{\beta })\\ \propto exp\left[-\frac{1}{2}\left\{\frac{1}{{\sigma }_{\mathit{Y}}^2}{\left(\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\right)}^T\left(\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\right)+\frac{1}{{\sigma }_{\mathit{\beta }}^2}{\mathit{\beta }}^T{\mathit{I}}^{-1}\mathit{\beta }\right\}\right]\\ \propto exp[-\frac{1}{2}\{{\mathit{\beta }}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{z}}^T\mathit{z}+\frac{1}{{\sigma }_{\mathit{\beta }}^2}\mathit{I}\right)\mathit{\beta }-2\left(\left({\mathit{Y}}^T-{\mathit{b}}^T{\mathit{Z}}^T-{\mathit{g}}^T{\mathit{M}}^T{\mathit{C}}^T\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{z}\right)\right)\mathit{\beta }\left\}\right]\end{array}$$

Therefore, by (A.1), the optimal density q^*(β) is

$$q^{\ast }(\mathit{\beta })\propto exp\left[-\frac{1}{2}{\text{E}}_{-\mathit{\beta }}\left\{{\mathit{\beta }}^T\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}{\mathit{z}}^T\mathit{z}+\frac{1}{{\sigma }_{\mathit{\beta }}^2}\mathit{I}\right)\mathit{\beta }-2\left(\left({\mathit{Y}}^T-{\mathit{b}}^T{\mathit{Z}}^T-{\mathit{g}}^T{\mathit{M}}^T{\mathit{C}}^T\right)\left(\frac{1}{{\sigma }_{\mathit{Y}}^2}\mathit{z}\right)\right)\mathit{\beta }\right\}\right].$$

After taking the expectation above, the optimal density q^*(β) is N(μ_q(β), Σ_q(β)) where

$$\begin{array}{l}{\mathbf{\sum }}_{q(\mathit{\beta })}={\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}{\mathit{z}}^T\mathit{z}+\frac{1}{{\sigma }_{\mathit{\beta }}^2}\mathit{I}\right\}}^{-1}\\ {\mathit{\mu }}_{q(\mathit{\beta })}={\mathbf{\sum }}_{q(\mathit{\beta })}{\left\{{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left({\mathit{Y}}^T-{\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{Z}}^T-{\mathit{\mu }}_{q(\mathit{g})}^T\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}^T\right)\mathit{z}\right\}}^T.\end{array}$$ (A.8)

A.5. Optimal density for ${\sigma }_X^2$

Recall that the functional predictors are observed over a grid of length N. The full conditional $p({\sigma }_{\mathit{X}}^2\mid \text{rest})$ is given by

$$\begin{array}{l}p({\sigma }_{\mathit{X}}^2\mid \text{rest})\propto p(\mathit{W}\mid {\sigma }_{\mathit{X}}^2)p({\sigma }_{\mathit{X}}^2)\\ \propto \left[\prod _{i=1}^I\prod _{j=1}^J{({\sigma }_{\mathit{X}}^2)}^{-N/2}exp\left\{-\frac{1}{2{\sigma }_{\mathit{X}}^2}(W_{ij}-C_{ij}{\mathit{\psi }}^T){(W_{ij}-C_{ij}{\mathit{\psi }}^T)}^T\right\}\right]·\left[{({\sigma }_{\mathit{X}}^2)}^{-A_{\mathit{X}}-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{X}}^2}{B}_{\mathit{X}}\right\}\right]\\ ={({\sigma }_{\mathit{X}}^2)}^{-A_{\mathit{X}}-(\mathit{nJN})/2-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{X}}^2}(B_{\mathit{X}}+\frac{1}{2}\sum _{i=1}^I\sum _{j=1}^J({\mathit{W}}_{ij}-{\mathit{C}}_{ij}{\mathit{\psi }}^T){({\mathit{W}}_{ij}-{\mathit{C}}_{ij}{\mathit{\psi }}^T)}^T)\right\}\end{array}$$

so that the optimal density $q^{\ast }{\sigma }_{\mathit{X}}^2$ is

$$q^{\ast }({\sigma }_{\mathit{X}}^2)\propto exp\{-A_{\mathit{X}}+(\mathit{nNJ}/2+1)log({\sigma }_{\mathit{X}}^2)-\frac{1}{{\sigma }_{\mathit{X}}^2}\left(B_{\mathit{X}}+\frac{1}{2}{\text{E}}_{-{\sigma }_{\mathit{X}}^2}\sum _{i=1}^I\sum _{j=1}^J({\mathit{W}}_{ij}-{\mathit{C}}_{ij}{\mathit{\psi }}^T){({\mathit{W}}_{ij}-{\mathit{C}}_{ij}{\mathit{\psi }}^T)}^T\right)\}.$$

Thus $q^{\ast }({\sigma }_{\mathit{X}}^2)$ is $\text{IG}(A_{\mathit{X}}+(\mathit{nNJ})/2,B_{q({\sigma }_{\mathit{X}}^2)})$ where

$$B_{q({\sigma }_{\mathit{X}}^2)}=B_{\mathit{X}}+\frac{1}{2}\left\{\sum _{i=1}^I\sum _{j=1}^J{\left|\right|{({\mathit{W}}_{ij}-{\mathit{\mu }}_{q(\mathit{c}),ij}{\mathit{\psi }}^T)}^T\left|\right|}^2+(nJ)\text{tr}\left({\mathit{\psi }}^T\mathit{\psi }{\mathbf{\sum }}_{q(\mathit{C})}\right)\right\}$$ (A.9)

Note that, when $q({\sigma }_{\mathit{X}}^2)=q^{\ast }({\sigma }_{\mathit{X}}^2)$, the term ${\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}$ appearing in (A.6) is equal to $\frac{A_{\mathit{X}}+nJ/2}{B_{q({\sigma }_{\mathit{X}}^2)}}$.

A.6. Optimal density for ${\sigma }_Y^2$

Finally, the full conditional $p({\sigma }_{\mathit{Y}}^2\mid \text{rest})$ is given by

$$\begin{array}{l}p({\sigma }_{\mathit{Y}}^2\mid \text{rest})\propto p(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)p({\sigma }_{\mathit{Y}}^2)\\ \propto {({\sigma }_{\mathit{Y}}^2)}^{-(nJ)/2}exp\left\{-\frac{1}{2{\sigma }_{\mathit{Y}}^2}{\left|\right|\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\left|\right|}^2\right\}\times {({\sigma }_{\mathit{Y}}^2)}^{-A_{\mathit{Y}}-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{Y}}^2}{B}_{\mathit{Y}}\right\}\\ ={({\sigma }_{\mathit{Y}}^2)}^{-A_{\mathit{Y}}/(nJ)/2-1}exp\left\{-\frac{1}{{\sigma }_{\mathit{Y}}^2}\left(B_{\mathit{Y}}+\frac{1}{2}{\left|\right|\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\left|\right|}^2\right)\right\}\end{array}$$

so that the optimal density $q^{\ast }({\sigma }_{\mathit{Y}}^2)$ is

$$q^{\ast }({\sigma }_{\mathit{Y}}^2)\propto exp\{-(A_{\mathit{Y}}+(nJ)/2+1)log({\sigma }_{\mathit{Y}}^2)-\frac{1}{{\sigma }_{\mathit{Y}}^2}\left(B_{\mathit{Y}}+\frac{1}{2}{\text{E}}_{-{\sigma }_{\mathit{Y}}^2}{\left|\right|\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\left|\right|}^2\right)\}.$$

Next, we see that

$$\begin{array}{l}{\text{E}}_{-{\sigma }_{\mathit{Y}}^2}\left\{{\left|\right|\mathit{Y}-\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{Zb}-{\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\left|\right|}^2\right\}\\ ={\left|\right|\mathit{Y}-\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{Zb}-{\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\left|\right|}^2\\ +{\text{E}}_{-{\sigma }_{\mathit{Y}}^2}\left\{{(\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{z}\mathit{\beta })}^T(\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{z}\mathit{\beta })\right\}\\ +{\text{E}}_{-{\sigma }_{\mathit{Y}}^2}\left\{{({\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}-\mathit{CMg})}^T({\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}-\mathit{CMg})\right\}\\ +{\text{E}}_{-{\sigma }_{\mathit{Y}}^2}\left\{{(\mathit{Z}{\mathit{\mu }}_{q(\mathit{b})}-\mathit{Zb})}^T(\mathit{Z}{\mathit{\mu }}_{q(\mathit{b})}-\mathit{Zb})\right\}\\ ={\left|\right|\mathit{Y}-\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{Zb}-{\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\left|\right|}^2+\text{tr}({\mathit{z}}^T\mathit{z}{\mathbf{\sum }}_{q(\mathit{\beta })})\\ -{\left({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}\right)}^T\left({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}\right)\\ +{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\\ +\text{tr}\left\{{\mathit{M}}^T\left({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})}\right)\mathit{M}{\mathbf{\sum }}_{q(\mathit{g})}\right\}\\ +\text{tr}\left\{{\mathit{Z}}^T\mathit{Z}{\mathbf{\sum }}_{q(\mathit{b})}\right\}.\end{array}$$ (A.10)

Thus $q^{\ast }({\sigma }_{\mathit{Y}}^2)$ is $\text{IG}(A_{\mathit{Y}}+(nJ)/2,B_{q({\sigma }_{\mathit{Y}}^2)})$ where

$$\begin{array}{l}{B}_{q({\sigma }_{\mathit{Y}}^2)}=B_{\mathit{Y}}+\frac{1}{2}[{\left|\right|\mathit{Y}-\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{Zb}-{\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\left|\right|}^2+\text{tr}\left({\mathit{z}}^T\mathit{z}{\mathbf{\sum }}_{q(\mathit{\beta })}\right)\\ -{\left({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}\right)}^T\left({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}\right)\\ +{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\\ +\text{tr}\left\{{\mathit{M}}^T\left({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})}\right)\mathit{M}{\mathbf{\sum }}_{q(\mathit{g})}\right\}+\text{tr}\left\{{\mathit{Z}}^T\mathit{Z}{\mathbf{\sum }}_{q(\mathit{b})}\right\}]\end{array}$$ (A.11)

Note that, when $q({\sigma }_{\mathit{Y}}^2)=q_{{\sigma }_{\mathit{Y}}^2}^{\ast }({\sigma }_{\mathit{Y}}^2)$, the term ${\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}$ appearing regularly above is equal to $\frac{A_{\mathit{Y}}+(nJ)/2}{B_{q({\sigma }_{\mathit{Y}}^2)}}$.

Appendix B: Expression for p(Y, W; q)

In this appendix we derive an expression for the lower bound of the log likelihood. This quantity is use to monitor convergence in Algorithm 1, and its derivation takes advantage of the order of updates in the algorithm to simplify the expression.

We have that $log\underset{\_}{p}(\mathit{Y},\mathit{W};q^{\ast })=\int q(\mathit{\theta })log(\frac{p(\mathit{Y},\mathit{W},\mathit{\theta })}{q^{\ast }(\mathit{\theta })})d\mathit{\theta }={\text{E}}_{q^{\ast }}[logp(\mathit{Y},\mathit{W},\mathit{\theta })-log{q}^{\ast }(\mathit{\theta })]$. Now,

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{Y},\mathit{W},\mathit{\theta })-log{q}^{\ast }(\mathit{\theta })]\\ ={\text{E}}_{q^{\ast }}[logp(\mathit{Y}\mid ,\mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)]+{\text{E}}_{q^{\ast }}[logp(\mathit{W}\mid \mathit{C},{\sigma }_{\mathit{X}}^2)]\\ +{\text{E}}_{q^{\ast }}[logp(\mathit{\beta })-log\{q^{\ast }(\mathit{\beta })\}]+{\text{E}}_{q^{\ast }}[logp(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)-log\{q^{\ast }(\mathit{g})\}]\\ +{\text{E}}_{q^{\ast }}[logp(\mathit{b}\mid {\sigma }_{\mathit{b}}^2)-log\{q^{\ast }(\mathit{b})\}]+{\text{E}}_{q^{\ast }}[logp(\mathit{C}\mid \lambda )-log\{q^{\ast }(\mathit{C})\}]\\ +{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{g}}^2)-log\{q^{\ast }({\sigma }_{\mathit{g}}^2)\}]+{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{b}}^2)-log\{q^{\ast }({\sigma }_{\mathit{b}}^2)\}]\\ +{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{Y}}^2)-log\{q^{\ast }({\sigma }_{\mathit{Y}}^2)\}]+{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{X}}^2)-log\{q^{\ast }({\sigma }_{\mathit{X}}^2)\}]\\ +\sum _{k=1}^{K_x}{\text{E}}_{q^{\ast }}[logp({\lambda }_k)-log\{q^{\ast }({\lambda }_k)\}]\end{array}$$ (B.1)

The first term appearing in (B.1) is

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2]\\ ={\text{E}}_{q^{\ast }}\left[-\frac{nJ}{2}log(2\pi )-\frac{1}{2}log(\mid {\sigma }_{\mathit{Y}}^2\mathit{I}\mid )-\frac{1}{2}\frac{1}{{\sigma }_{\mathit{Y}}^2}{\left|\right|\mathit{Y}-\mathit{z}\mathit{\beta }-\mathit{Zb}-\mathit{CMg}\left|\right|}^2\right]\\ =-\frac{nJ}{2}log(2\pi )-\frac{nJ}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{Y}}^2)\\ -\frac{1}{2}{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\{{\left|\right|\mathit{Y}-\mathit{z}{\mathit{\mu }}_{q(\mathit{\beta })}-\mathit{Zb}-{\mathit{\mu }}_{q(\mathit{C})}\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\left|\right|}^2+\text{tr}({\mathit{z}}^T\mathit{z}{\mathbf{\sum }}_{q(\mathit{\beta })})\\ -{\left({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}\right)}^T\left({\mathit{\mu }}_{q(\mathit{g})}\mathit{M}{\mathit{\mu }}_{q(\mathit{C})}\right)\\ +{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{M}}^T({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})})\mathit{M}{\mathit{\mu }}_{q(\mathit{g})}\\ +\text{tr}\left\{{\mathit{M}}^T\left({\mathit{\mu }}_{q(\mathit{C})}^T{\mathit{\mu }}_{q(\mathit{C})}+(nJ){\mathbf{\sum }}_{q(\mathit{C})}\right)\mathit{M}{\mathbf{\sum }}_{q(\mathit{g})}\right\}+\text{tr}\left\{{\mathit{Z}}^T\mathit{Z}{\mathbf{\sum }}_{q(\mathit{b})}\right\}\}.\end{array}$$

The second term is

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{W}\mid \mathit{C},{\sigma }_{\mathit{X}}^2)]={\text{E}}_{q^{\ast }}\left[\sum _{i=1}^n\sum _{j=1}^J\left(\frac{-N}{2}log(2\pi )-\frac{N}{2}log({\sigma }_{\mathit{X}}^2)-\frac{1}{2}\frac{1}{{\sigma }_{\mathit{X}}^2}{\left|\right|{\left({\mathit{W}}_{ij}-{\mathit{C}}_{ij}{\mathit{\psi }}^T\right)}^T\left|\right|}^2\right)\right]\\ =-\frac{\mathit{nJN}}{2}log(2\pi )-\frac{\mathit{nJN}}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{X}}^2)-\frac{1}{2}{\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}\left[\sum _{i=1}^n\sum _{j=1}^J{\left|\right|{({\mathit{W}}_{ij}-{\mathit{\mu }}_{q(\mathit{c}),ij}{\mathit{\psi }}^T)}^T\left|\right|}^2+(nJ)\text{tr}\left({\mathit{\psi }}^T\mathit{\psi }{\mathbf{\sum }}_{q(\mathit{C})}\right)\right].\end{array}$$

Next, we have

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{\beta })-log\{q^{\ast }(\mathit{\beta })\}]={\text{E}}_{q^{\ast }}\left[\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{\beta })}\mid }{{\sigma }_{\beta }^{2p}}\right)-\frac{1}{2{\sigma }_{\mathit{\beta }}^2}{\mathit{\beta }}^T\mathit{\beta }+\frac{1}{2}{(\mathit{\beta }-{\mathit{\mu }}_{q(\mathit{\beta })})}^T{\mathbf{\sum }}_{q(\mathit{\beta })}^{-1}(\mathit{\beta }-{\mathit{\mu }}_{q(\mathit{\beta })})\right]\\ =\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{\beta })}\mid }{{\sigma }_{\beta }^{2p}}\right)-\frac{1}{2{\sigma }_{\mathit{\beta }}^2}\left\{{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{\mu }}_{q(\mathit{\beta })}+\text{tr}({\mathbf{\sum }}_{q(\mathit{\beta })})\right\}+\frac{p}{2}.\end{array}$$

The fourth term is given by

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{g}\mid {\sigma }_{\mathit{g}}^2)-log\{q^{\ast }(\mathit{g})\}]={\text{E}}_{q^{\ast }}\left[\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{g})}\mid }{\mid {\sigma }_{\mathit{g}}^{2}D\mid }\right)-\frac{1}{2}\frac{1}{{\sigma }_{\mathit{g}}^2}{\mathit{g}}^T{\mathit{D}}^{-1}\mathit{g}+\frac{1}{2}{(\mathit{g}-{\mathit{\mu }}_{q(\mathit{g})})}^T{\mathbf{\sum }}_{q(\mathit{g})}^{-1}(\mathit{g}-{\mathit{\mu }}_{q(\mathit{g})})\right]\\ =\frac{1}{2}log(\mid {\mathbf{\sum }}_{q(\mathit{g})}\mid )-\frac{K_g}{2}{\text{E}}_{q^{\ast }}[log{\sigma }_{\mathit{g}}^2]-\frac{1}{2}log(\mid \mathit{D}\mid )-{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}\frac{1}{2}\left\{{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{D}}^{-1}{\mathit{\mu }}_{q(\mathit{g})}+\text{tr}({\mathit{D}}^{-1}{\mathbf{\sum }}_{q(\mathit{g})})\right\}\frac{K_g}{2}.\end{array}$$

Further, we have

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{C}\mid \mathrm{\Lambda })-log\{q^{\ast }(\mathit{C})\}]={\text{E}}_{q^{\ast }}[\sum _{k=1}^{K_x}\{\frac{nJ}{2}log\left(\frac{{({\mathbf{\sum }}_{q(\mathit{C})})}_{kk}}{{\lambda }_k}\right)-\frac{1}{2}\frac{1}{{\lambda }_k}{\mathit{C}}_k^T{\mathit{C}}_k+\frac{1}{2}{\left(({\mathit{C}}^k)-{({\mathit{\mu }}_{q(\mathit{C})}^k)}^T\right)}^T{({\mathbf{\sum }}_{q(\mathit{C})}^{-1})}_{kk}\left(({\mathit{C}}^k)-{({\mathit{\mu }}_{q(\mathit{C})}^k)}^T\right)\}]\\ =\sum _{k=1}^{K_x}\frac{nJ}{2}log\{{({\mathbf{\sum }}_{q(\mathit{C})})}_{kk}\}-\sum _{k=1}^{K_x}\frac{nJ}{2}{\text{E}}_{q^{\ast }}log({\lambda }_k)-\sum _{j=1}^{K_x}\frac{1}{2}{\mu }_{q(1/{\lambda }_k)}\left({({\mathit{\mu }}_{q(\mathit{C})}^k)}^T({\mathit{\mu }}_{q(\mathit{C})}^k)+(nJ){({\mathbf{\sum }}_{q(\mathit{C})})}_{kk}\right)+\frac{(nJ)K_x}{2}.\end{array}$$

The sixth term in (B.1) is

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp(\mathit{b}\mid {\sigma }_{\mathit{b}}^2)-q^{\ast }(\mathit{b})]={\text{E}}_{q^{\ast }}\left[\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{b})}\mid }{\mid {\sigma }_{\mathit{b}}^2\mathit{I}\mid }\right)-\frac{1}{2}\frac{1}{{\sigma }_{\mathit{b}}^2}{\mathit{b}}^T\mathit{b}+\frac{1}{2}{(\mathit{b}-{\mathit{\mu }}_{q(\mathit{b})})}^T{\mathbf{\sum }}_{q(\mathit{b})}^{-1}(\mathit{b}-{\mathit{\mu }}_{q(\mathit{b})})\right]\\ =\frac{1}{2}{\text{E}}_{q^{\ast }}[log(\mid {\mathbf{\sum }}_{q(\mathit{b})}\mid )-\frac{n}{2}{\text{E}}_{q^{\ast }}[log{\sigma }_{\mathit{b}}^2]-{\mu }_{q(1/{\sigma }_{\mathit{b}}^2)}\frac{1}{2}\left[{\mathit{\mu }}_{q(\mathit{b})}^T{\mathit{\mu }}_{q(\mathit{b})}+\text{tr}({\mathbf{\sum }}_{q(\mathit{b})})\right]+\frac{n}{2}.\end{array}$$

Next,

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{g}}^2)-log\{q^{\ast }({\sigma }_{\mathit{g}}^2)\}]\\ =\frac{K_g}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{g}}^2)+{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}\left(B_{q({\sigma }_{\mathit{g}}^2)}-B_{\mathit{g}}\right)+A_{\mathit{g}}log(B_{\mathit{g}})-log\{\mathrm{\Gamma }(A_{\mathit{g}})\}\\ -\left(A_{\mathit{g}}+\frac{K_g}{2}\right)log\left(B_{q({\sigma }_{\mathit{g}}^2)}\right)+log\left\{\mathrm{\Gamma }\left(A_{\mathit{g}}+\frac{K_g}{2}\right)\right\}.\end{array}$$

Additionally, the eighth term in (B.1) is

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{b}}^2)-log\{q^{\ast }({\sigma }_{\mathit{b}}^2)\}]\\ =\frac{n}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{b}}^2)+{\mu }_{q(1/{\sigma }_{\mathit{b}}^2)}\left(B_{q({\sigma }_{\mathit{b}}^2)}-B_{\mathit{b}}\right)+A_{\mathit{b}}log(B_{\mathit{b}})-log\{\mathrm{\Gamma }(A_{\mathit{b}})\}\\ -\left(A_{\mathit{b}}+\frac{n}{2}\right)log\left(B_{q({\sigma }_{\mathit{b}}^2)}\right)+log\left\{\mathrm{\Gamma }\left(A_{\mathit{b}}+\frac{n}{2}\right)\right\}.\end{array}$$

Next, we have

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{Y}}^2)-log\{q^{\ast }({\sigma }_{\mathit{Y}}^2)\}]\\ =\frac{nJ}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{Y}}^2)+{\mu }_{q(1/{\sigma }_{\mathit{Y}}^2)}\left(B_{q({\sigma }_{\mathit{Y}}^2)}-B_{\mathit{Y}}\right)+A_{\mathit{Y}}log(B_{\mathit{Y}})-log\{\mathrm{\Gamma }(A_{\mathit{Y}})\}\\ -\left(A_{\mathit{Y}}+\frac{n}{2}\right)log\left(B_{q({\sigma }_{\mathit{Y}}^2)}\right)+log\left\{\mathrm{\Gamma }\left(A_{\mathit{Y}}+\frac{n}{2}\right)\right\}\end{array}$$

The tenth term is

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{X}}^2)-log\{q^{\ast }({\sigma }_{\mathit{X}}^2)\}]\\ =\frac{\mathit{nJN}}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{X}}^2)+{\mu }_{q(1/{\sigma }_{\mathit{X}}^2)}\left(B_{q({\sigma }_{\mathit{X}}^2)}-B_{\mathit{X}}\right)+A_{\mathit{X}}log(B_{\mathit{X}})\\ -log\{\mathrm{\Gamma }(A_{\mathit{X}})\}-\left(A_{\mathit{X}}+\frac{\mathit{nJN}}{2}\right)log\left(B_{q({\sigma }_{\mathit{X}}^2)}\right)+log\left\{\mathrm{\Gamma }\left(A_{\mathit{X}}+\frac{\mathit{nJN}}{2}\right)\right\}\end{array}$$

Finally, for 1 ≤ k ≤ K_x

$$\begin{array}{l}{\text{E}}_{q^{\ast }}[logp({\lambda }_k)-log\{q^{\ast }({\lambda }_k)\}]\\ =\frac{nJ}{2}{\text{E}}_{q^{\ast }}log({\lambda }_k)+{\mu }_{q(1/{\lambda }_K)}\left(B_{q({\lambda }_k)}-B_{\lambda }\right)+A_{\lambda }log(B_{\lambda })-log\{\mathrm{\Gamma }(A_{\lambda })\}\\ -\left(A_{\lambda }+\frac{nJ}{2}\right)log\left(B_{q({\lambda }_k)}\right)+log\left\{\mathrm{\Gamma }\left(A_{\lambda }+\frac{nJ}{2}\right)\right\}\end{array}$$

We combine the above factors noting that many terms cancel. For example, the terms $-\frac{nJ}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{Y}}^2)$ and $\frac{nJ}{2}{\text{E}}_{q^{\ast }}log({\sigma }_{\mathit{Y}}^2)$ appear in ${\text{E}}_{q^{\ast }}[logp(\mathit{Y}\mid \mathit{\beta },\mathit{b},\mathit{C},\mathit{g},{\sigma }_{\mathit{Y}}^2)]$ and ${\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{Y}}^2)-log\{q^{\ast }({\sigma }_{\mathit{Y}}^2)]$ respectively. Moreover, we can make substitutions for terms appearing in the updates given in Algorithm 1 and again simplify the expression. An example is to combine $-{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}{B}_{\mathit{g}}$ and $-{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}\frac{1}{2}[{\mathit{\mu }}_{q(\mathit{g})}^T{\mathit{D}}^{-1}{\mathit{\mu }}_{q(\mathit{g})}+\text{tr}({\mathit{D}}^{-1}{\mathbf{\sum }}_{q(\mathit{b})})]$ and substitute for $-{\mu }_{q(1/{\sigma }_{\mathit{g}}^2)}{B}_{q({\sigma }_{\mathit{g}}^2)}$; this term cancels with another appearing in ${\text{E}}_{q^{\ast }}[logp({\sigma }_{\mathit{g}}^2)-log\{q^{\ast }({\sigma }_{\mathit{g}}^2)\}]$. Thus we have

$$\begin{array}{l}log\underset{\_}{p}(\mathit{Y},\mathit{W};q)\\ =\frac{-nJ}{2}log(2\pi )+\frac{-\mathit{nJN}}{2}log(2\pi )\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{\beta })}\mid }{{\sigma }_{\beta }^{2p}}\right)\\ -\frac{1}{2{\sigma }_{\mathit{\beta }}^2}\left\{{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{\mu }}_{q(\mathit{\beta })}+\text{tr}({\mathbf{\sum }}_{q(\mathit{\beta })})\right\}+\frac{p}{2}\\ +\frac{1}{2}log(\mid {\mathbf{\sum }}_{q(\mathit{g})}\mid )]+\frac{K_g}{2}+\sum _{k=1}^{K_x}\frac{nJ}{2}log({({\mathbf{\sum }}_{q(\mathit{C})})}_{kk})+\frac{{\mathit{nJK}}_x}{2}\\ +\frac{1}{2}log(\mid {\mathbf{\sum }}_{q(\mathit{b})}\mid )+\frac{n}{2}\\ +A_{\mathit{g}}log(B_{\mathit{g}})-log(\mathrm{\Gamma }(A_{\mathit{g}}))-\left(A_{\mathit{g}}+\frac{K_g}{2}\right)log\left(B_{q({\sigma }_g^2)}\right)\\ +log\left\{\mathrm{\Gamma }\left(A_{\mathit{g}}+\frac{K_g}{2}\right)\right\}\\ +A_{\mathit{b}}log(B_{\mathit{b}})-log(\mathrm{\Gamma }(A_{\mathit{b}}))-\left(A_{\mathit{b}}+\frac{n}{2}\right)log\left(B_{q({\sigma }_{\mathit{b}}^2)}\right)+log\left\{\mathrm{\Gamma }\left(A_{\mathit{b}}+\frac{n}{2}\right)\right\}\\ +A_{\mathit{Y}}log(B_{\mathit{Y}})-log(\mathrm{\Gamma }(A_{\mathit{Y}}))-\left(A_{\mathit{Y}}+\frac{nJ}{2}\right)log\left(B_{q({\sigma }_{\mathit{Y}}^2)}\right)\\ +log\left\{\mathrm{\Gamma }\left(A_{\mathit{Y}}+\frac{nJ}{2}\right)\right\}\\ +A_{\mathit{X}}log(B_{\mathit{X}})-log(\mathrm{\Gamma }(A_{\mathit{X}}))-\left(A_{\mathit{X}}+\frac{\mathit{nJN}}{2}\right)log\left(B_{q({\sigma }_{\mathit{X}}^2)}\right)\\ +log\left\{\mathrm{\Gamma }\left(A_{\mathit{X}}+\frac{\mathit{nJN}}{2}\right)\right\}\\ +\sum _{k=1}^{K_x}[A_{\lambda }log(B_{\lambda })-log(\mathrm{\Gamma }(A_{\lambda }))-\left(A_{\lambda }+\frac{nJ}{2}\right)log\left(B_{q({\lambda }_k)}\right)\\ +log\{\mathrm{\Gamma }\left(A_{\lambda }+\frac{nJ}{2}\right)\left\{\right]\end{array}$$

Using const. to represent an additive constant that is not affected by updates in Algorithm 1, we have

$$\begin{array}{l}log\underset{\_}{p}(\mathit{Y},\mathit{W};q)\\ =\frac{1}{2}log\left(\frac{\mid {\mathbf{\sum }}_{q(\mathit{\beta })}\mid }{{\sigma }_{\beta }^{2p}}\right)-\frac{1}{2{\sigma }_{\mathit{\beta }}^2}\left\{{\mathit{\mu }}_{q(\mathit{\beta })}^T{\mathit{\mu }}_{q(\mathit{\beta })}+\text{tr}({\mathbf{\sum }}_{q(\mathit{\beta })})\right\}\\ +\frac{1}{2}{\text{E}}_{q^{\ast }}[log(\mid {\mathbf{\sum }}_{q(\mathit{g})}\mid )]+\sum _{k=1}^{K_x}\frac{nJ}{2}log({({\mathbf{\sum }}_{q(\mathit{C})})}_{kk})+\frac{1}{2}{\text{E}}_{q^{\ast }}[log(\mid {\mathbf{\sum }}_{q(\mathit{b})}\mid )]\\ -\left(A_{\mathit{g}}+\frac{K_g}{2}\right)log\left(B_{q({\sigma }_{\mathit{g}}^2)}\right)-\left(A_{\mathit{b}}+\frac{n}{2}\right)log\left(B_{q({\sigma }_{\mathit{b}}^2)}\right)\\ -\left(A_{\mathit{Y}}+\frac{nJ}{2}\right)log\left(B_{q({\sigma }_{\mathit{Y}}^2)}\right)\\ -\left(A_{\mathit{X}}+\frac{\mathit{nJN}}{2}\right)log\left(B_{q({\sigma }_{\mathit{X}}^2)}\right)-\sum _{k=1}^{K_x}\left\{\left(A_{\lambda }+\frac{nJ}{2}\right)log\left(B_{q({\lambda }_k)}\right)\right\}+\text{const}.\end{array}$$