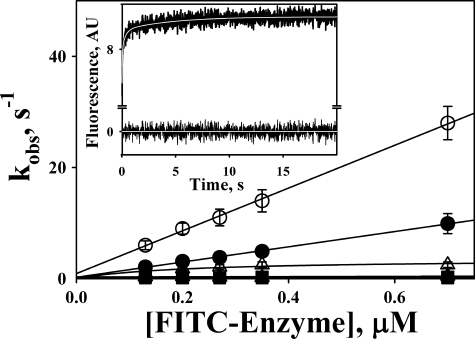
FIGURE 5.
Stopped-flow kinetics of interaction of TEX615-oligo(dAT)33 with FITC-tctPA (filled symbols) and FITC-tcuPA (open symbols). The dependences of kobs,1 (circles); kobs,2 (triangles), and kobs,3 (squares) obtained from the best fit of the three-exponential equation to stopped-flow traces (inset) on [FITC-enzyme] are shown. Solid lines represent the best fit of linear equations kobs,1 = k−1 + k+1·[FITC-enzyme] (○ and ●); kobs = const (▴, □, and ■); and the best fit of a hyperbolic equation kobs = klim·[FITC-enzyme]/(K0.5 + [FITC-enzyme] (Δ), where klim is kobs at infinite [FITC-Enzyme] and K0.5 is the [FITC-enzyme] at kobs = klim/2. The values of the rate constants for the first, second, and third step of the mechanism of interaction between TEX615-oligo(dAT)33 with FITC-tctPA were 14 ± 2 μm−1s−1 and 0.35 ± 0.10 and 0.10 ± 0.02 s−1 and with FITC-tcuPA were 39 ± 4 μm−1s−1 and 3.5 ± 0.7 and 0.30 ± 0.05 s−1, respectively. Inset, time dependence of the changes in fluorescence emission, monitored through a 650-nm cutoff filter (excitation at 493 nm), due to the interaction of FITC-uPA (0.35 μm) and TEX615-oligo(dAT)33 (30 nm). Pro-Data Viewer software (Applied Photophysics Ltd.) was employed to fit single, two-, and three-exponential equations to the data. The white line inside the trace represents the best fit of a three-exponential equation, Ft = F∞ + A1·e−(kobs,1)t + A2·e−(kobs,2)t + A3·e−(kobs,3)t (where Ft is the fluorescence emission at time t; F∞ is the final fluorescence (AU); kobs and A are observed rate constants and amplitudes, respectively), to the data. Residuals are shown below the trace.