Abstract
Rodents are defined by a uniquely specialized dentition and a highly complex arrangement of jaw-closing muscles. Finite element analysis (FEA) is an ideal technique to investigate the biomechanical implications of these specializations, but it is essential to understand fully the degree of influence of the different input parameters of the FE model to have confidence in the model's predictions. This study evaluates the sensitivity of FE models of rodent crania to elastic properties of the materials, loading direction, and the location and orientation of the models’ constraints. Three FE models were constructed of squirrel, guinea pig and rat skulls. Each was loaded to simulate biting on the incisors, and the first and the third molars, with the angle of the incisal bite varied over a range of 45°. The Young's moduli of the bone and teeth components were varied between limits defined by findings from our own and previously published tests of material properties. Geometric morphometrics (GMM) was used to analyse the resulting skull deformations. Bone stiffness was found to have the strongest influence on the results in all three rodents, followed by bite position, and then bite angle and muscle orientation. Tooth material properties were shown to have little effect on the deformation of the skull. The effect of bite position varied between species, with the mesiodistal position of the biting tooth being most important in squirrels and guinea pigs, whereas bilateral vs. unilateral biting had the greatest influence in rats. A GMM analysis of isolated incisor deformations showed that, for all rodents, bite angle is the most important parameter, followed by elastic properties of the tooth. The results here elucidate which input parameters are most important when defining the FE models, but also provide interesting glimpses of the biomechanical differences between the three skulls, which will be fully explored in future publications.
Keywords: finite element analysis, geometric morphometrics, material properties, rodents, sensitivity analysis
Introduction
Containing well over 2000 species, the Rodentia is by far the most speciose order of mammals (Wilson & Reeder, 2005). It is also particularly interesting from a biomechanical perspective owing to the unique specializations of the feeding apparatus found in this group. All rodents possess a pair of grossly enlarged, continually growing incisors in both the upper and lower jaws, followed by a highly reduced post-incisor dentition – usually just three or four premolars and molars (Nowak, 1999). The incisors and cheek teeth are separated by a large diastema which, combined with a mandible that is foreshortened relative to the skull, has separated incisor gnawing from molar chewing. That is, when the molars are in occlusion, the incisors do not meet, and vice versa, so that the two feeding modes have become mutually exclusive activities (Hiiemae & Ardran, 1968). Indeed, to bring the incisors and molars into and out of occlusion, part of the masticatory musculature has been adapted to effect propalineal movement of the lower jaw (Becht, 1953).
The highly specialized morphology of the masticatory musculature has, in the past, been used to classify the rodents (Brandt, 1855; Simpson, 1945). Almost all extant rodents exhibit one of three distinct morphologies of the masseter muscle, known as the sciuromorph (squirrel-like), hystricomorph (porcupine-like) and myomorph (mouse-like) conditions (Wood, 1965). Each of these morphologies represents an expansion of part of the masseter on to the rostrum, as illustrated in Fig. 1 (see Cox & Jeffery, 2011 for anatomical details). Recent molecular phylogenetic work (Adkins et al. 2003; Blanga-Kanfi et al. 2009) has indicated that the sciuromorphs, hystricomorphs and myomorphs are not monophyletic groups and should not be used a basis for classification. Nevertheless, the terms sciuromorph, hystricomorph and myomorph have been retained by many modern researchers as descriptors of skull and masseter morphology, free from the implication of phylogenetic relationship (e.g. Hautier et al. 2010).
Fig. 1.
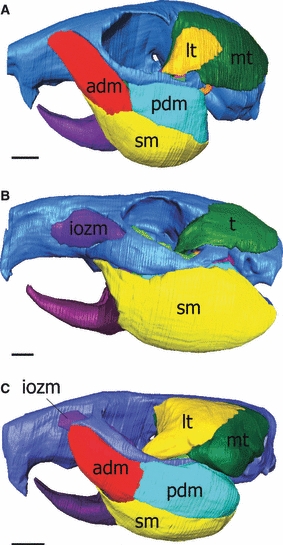
Three-dimensional reconstructions of the skull, mandible and masticatory muscles of (A) squirrel (sciuromorph), (B) guinea pig (hystricomorph) and (C) rat (myomorph). adm, anterior deep masseter; iozm, infraorbital part of the zygomatico-mandibularis; lt, lateral temporalis; mt, medial temporalis; pdm, posterior deep masseter; sm, superior masseter; t, temporalis. Scale bars: 5 mm.
Many previous studies have sought to determine the biomechanical outcomes of the complex muscle morphology in the rodents. This has usually been achieved by studying feeding in vivo with electromyography (e.g. Hiiemae & Ardran, 1968; Weijs & Dantuma, 1975; Gorniak, 1977; Byrd, 1981) or by estimation of muscle forces and lines of action from dissection (e.g. Hiiemae, 1971; Satoh, 1997, 1998, 1999; Vassallo & Verzi, 2001; Olivares et al. 2004; Druzinsky, 2010). A limited number of studies have sought to measure the bite force generated by rodents, although, due to the relative inaccessibility of the molars, this has largely been restricted to investigations of incisal biting (Robins, 1977; Nies & Ro, 2004; Freeman & Lemen, 2008). This current study simulates the biomechanics of rodent feeding using finite element analysis (FEA), a computational technique that predicts deformation, stress and strain in a structure when subjected to external loading conditions. Developed as an engineering tool for simulating the behaviour of man-made objects, FEA has more recently been employed by biologists to understand the mechanics of biological structures, in particular the vertebrate skull (e.g. Rayfield, 2004; Moreno et al. 2008; Moazen et al. 2009). Typically, FEA has been used to assess the biomechanical performance of varying skull geometries under controlled loading conditions approximating those experienced in real life (e.g. Dumont et al. 2005, 2010; Rayfield, 2005; McHenry et al. 2007; Wroe et al. 2007). However, there is also a body of work that investigates the effect of varying input parameters (material properties, muscle loadings) on the outcome of an FE analysis primarily as a means to define confidence in their findings, but also as a way to accommodate biological stochasticity and to capture normal ranges of variation induced by processes such as muscle fibre type transformation and osteoclast activity (Fagan et al. 2002; Ross et al. 2005; Kupczik et al. 2007; Reed et al. 2011).
Previous research has indicated that variation in the elastic properties of the model materials can have a large impact on the result of finite element analyses (Strait et al. 2005; Reed et al. 2011). Strait et al. (2005) found that, although variations in material property values had little effect on gross deformation patterns, the resulting numerical strain data were substantially affected by changes in bone stiffness. Similarly, the magnitude and orientation of the muscle forces applied to an FE model can also have a large effect on predicted strain values (Marinescu et al. 2005; Ross et al. 2005).
The aim of this study was to investigate the effect of varying input parameters on the outcomes of finite element analyses of rodent skulls. In particular, the material properties of the biological tissues were varied, along with the position of the bite along the tooth row and the angle at which biting occurs. Three rodents, representing the sciuromorph, hystricomorph and myomorph morphologies, were studied. The results were analysed using geometric morphometrics (GMM), a shape analysis technique that allows comparison of the skull deformations generated by the different loading regimes. The results will help elucidate the relative importance of input parameters, identifying those that can be generalized from those that are required to be known more precisely in future studies of the rodent skull.
Materials and methods
Sample
Three rodent species were chosen as representatives of the sciuromorph, hystricomorph and myomorph masseter morphologies. These were, respectively, the Eastern grey squirrel (Sciurus carolinensis), the domesticated guinea pig (Cavia porcellus) and the brown rat (Rattus norvegicus). These species were selected as they were thought to be typical members of each morphological group, i.e. none is anomalously specialized for a particularly unusual way of life or mode of feeding. To select an average individual of each species to study, formalin-fixed heads of eight rats, eight guinea pigs and seven squirrels were imaged using micro-computed tomography (microCT), carried out in the Department of Engineering, University of Hull. Field of view (FOV) varied from 27 to 50 mm and slice thickness from 0.047 to 0.076 mm. The total number of slices ranged from 990 to 1160. Subsequently, 43 three-dimensional landmarks (listed in Supporting Information Table S1) were taken from the skull of each specimen using amira 5.3.2 (Mercury Systems Inc., Chelmsford, MA, USA). From these data, variation in the shape of the skull within each species was analysed using geometric morphometrics (O'Higgins, 2000; Adams et al. 2004) as implemented within the evan toolkit (http://www.evan-society.org). The landmark co-ordinates were subjected to Procrustes superimposition to remove translation, rotation and size differences, and then a principal components analysis (PCA) was performed for each species. The Procrustes distance between each specimen and the origin was calculated as the square root of the summed squared principal component scores. The specimen with the shortest Procrustes distance to the origin within each species was judged to be the individual closest to the mean shape of the sample (which is located at the origin of the principal axes, O'Higgins, 2000), and this individual was used to construct the finite element model.
Model creation
One finite element model was constructed for the squirrel, guinea pig and rat, respectively from the microCT scans using amira 5.3.2. Each model comprised six separately thresholded volumes: skull, molar teeth, incisor enamel, incisor dentine, incisor pulp cavity and periodontal ligament (PDL); so that separate elastic properties could be applied to each of these materials. The enamel, dentine and pulp could not be adequately distinguished in the molar teeth, so these structures were modelled as a single volume. The models were smoothed and converted to a mesh in hypermesh 10.0 (Altair Engineering Inc., Troy, MI, USA). Each mesh was entirely composed of linear tetrahedral elements and ranged in size from 800 000 to 1.2 million elements (see Fig. 2).
Fig. 2.
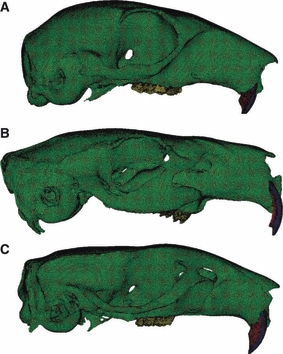
Three-dimensional FE models of the skull of a (A) squirrel, (B) guinea pig and (C) rat, constructed in hypermesh 10.0. Each mesh comprises between 0.8 and 1.2 million linear tetrahedral elements. Green, bone; blue, incisor enamel; red, incisor dentine; yellow, molar teeth.
Material properties
hypermesh 10.0 was also used to assign material properties to the elements and to add loads and constraints to each model. The Young's modulus (E) of each of the skeletal tissues was determined using a nano-hardness tester with a Berkovitch diamond indenter (CSM Instruments S.A., Peseux, Switzerland). The range of values measured was used as the range over which to vary the Young's modulus in the sensitivity analyses: bone, 10–30 GPa; incisor enamel, 60–80 GPa; incisor dentine, 15–25 GPa; molar teeth, 20–40 GPa. As the enamel and dentine could not be adequately distinguished in the molars, the cheek teeth were modelled as a single volume with a single elastic modulus. Values for Young's modulus of the pulp cavity and PDL were gathered from existing literature. Williams & Edmundson (1984) report a Young's modulus of 2 MPa for the pulp cavity. No other information on this material could be found, so it was decided to vary the pulp stiffness 10-fold in each direction, i.e. 0.2–20 MPa. In contrast, there is a wealth of literature on the Young's modulus of periodontal ligament, with values ranging over several orders of magnitude. Rees & Jacobsen (1997) report the range of values used for PDL in finite element studies. Three E values for PDL were used in this study: 0.7 MPa (Tanne et al. 1987), 50 MPa (Wilson, 1991) and 1750 MPa (Goel et al. 1992). Poisson's ratio for each material was gathered from existing literature (Williams & Edmundson, 1984) and ranged between 0.30 and 0.33 except for PDL and the pulp cavity (both 0.45). All materials were assumed to be linear and isotropic.
Muscle loads
To add muscle information to the FE models, the squirrel, guinea pig and rat specimens were subjected to the technique of contrast-enhanced microCT (Jeffery et al. 2011). The specimens were immersed in iodine solution for a number of weeks and then reimaged to reveal details of the masticatory muscle architecture. For details of the imaging protocol and descriptions of the rodent masticatory muscles, see Cox & Jeffery (2011). These scans were also used to generate three-dimensional reconstructions of the masticatory muscles (Fig. 1) to provide information on the origin sites of the muscles on the skull and from which muscle volumes could be measured. The contrast-enhanced images also allowed measurement of muscle fibre lengths; thus by dividing muscle volume by mean fibre length, it was possible to calculate the physiological cross-sectional area (PCSA) of each muscle. The superior masseter, deep masseter, zygomatico-mandibularis (anterior and posterior parts), temporalis, internal pterygoid and external pterygoid muscles were applied in each model. In addition, the infraorbital part of the zygomatico-mandibularis was modelled in the rat and guinea pig, and the deep masseter was modelled as separate anterior and posterior parts in the rat and squirrel (reflecting the difference in muscle morphology reported in Cox & Jeffery, 2011). Muscle forces were estimated by multiplying the PCSA by a muscle stress value of 0.3 N mm−2 (van Spronsen et al. 1989; Strait et al. 2005). Each estimated muscle force was distributed over multiple nodes (between 8 and 30) spread evenly across the corresponding muscle origination site. Muscle force orientations were determined by temporarily adding a reconstruction of the mandible to each model, so that a vector representing fibre direction could be created between the origin and insertion of each muscle. In the case of the temporalis, in which the fibres radiate from the insertion in a fan-shape and thus vary greatly in their orientation, individual vectors were created for each node selected at the origin.
The muscle force orientations were initially estimated with the mandible in a protracted position, that is, with the incisors in occlusion. To account for the antero-posterior movement of the lower jaw relative to the skull that is so characteristic of rodents, the mandible reconstruction was retracted to bring the molars into occlusion and the muscle force vectors were recalculated. Although not biologically realistic, it was decided to solve the models for both incisor and molar biting with both a protracted and a retracted mandible, to understand the impact of mandibular position on the results of the FE analysis.
Constraints
To constrain the models and prevent free body motion, three or four nodes were constrained in each mesh. A single node was constrained at each temporo-mandibular joint, on the underside of the zygomatic process of the squamosal. This node was constrained in all three axes on the left-hand side, but only two axes were constrained on the right, so that medio-lateral movement of the skull was allowed. Any more than one node constrained at each TMJ was found to over-constrain the skull and to produce very high local stresses around the TMJ. Additionally, a node was constrained at the bite point in the axis of biting. At the molars, this was always in a dorso-ventral direction, perpendicular to the occlusal plane. At the incisors, the axis of constraint was varied between 90° and 45° to the occlusal plane of the molars to simulate different gape angles. A constraint perpendicular to the occlusal plane represents a very narrow gape, whereas a constraint at 45° to the occlusal plane represents a wide gape. The bite point was varied between the incisors, the first molar (M1) and the third molar (M3). Both bilateral and unilateral molar bites are observed in rodents (Byrd, 1981) and so both were modelled in this analysis; incision was assumed always to be bilateral due to the close apposition of the incisors.
Model solution and analysis
The FE models were solved using abaqus 6.10.2 (Simulia, Providence, RI, USA). Each model was solved for two mandible positions, four incisor bite angles, four molar bites (M1 and M3, unilateral and bilateral), three E values for bone, enamel, molar teeth, pulp cavity and periodontal ligament, and two E values for dentine. Young's modulus of the incisor materials was held constant during molar biting and vice versa. To reduce the number of sensitivity analyses to be performed, the Young's moduli of pulp and PDL were fixed at 2 and 50 MPa, respectively, for most analyses and were only changed in particular instances. When pulp cavity stiffness was varied, all other tooth material properties were held constant and only bone stiffness and bite angle were allowed to change. When PDL was varied, all other material properties (including bone) were held constant and only bite position was changed. Similarly, most analyses were performed with a protracted mandible and only a small number were repeated with the mandible in the retracted position. In total, 390 separate analyses were carried out, 130 per model; these are listed in Supporting Information Table S2.
To compare the analyses numerically, the resulting deformed models were subjected to a geometric morphometric (GMM) form space analysis (O'Higgins et al. 2011), again performed using the evan toolkit (http://www.evan-society.org). To undertake this, 36 three-dimensional landmark co-ordinates, illustrated in Fig. 3, were recorded from each loaded skull as well as from the original unloaded models. The set of landmarks previously used to determine the ‘most average’ individual was not suitable for re-use here, as they were chosen for their ease of location on a stack of microCT images. The landmarks used to examine skull deformations needed to be easily locatable on a three-dimensional skull reconstruction in which many bone sutures were not visible. The landmarks were recorded from three areas of high strain – orbits, zygomatic arches and rostrum – as well as more widely across the skull to provide a general reflection of skull shape and deformation. Landmarks were defined as precisely as possible to allow homologous points to be chosen in all three species. Homology of landmarks between analyses within each species was absolute, as each node of the model was numbered by abaqus 6.10.2 and therefore the same node could be selected in each analysis. As before, the landmarks were subjected to a generalized Procrustes analysis and a principal components analysis, so that each set of deformations could be compared with the others and the original undeformed skull. The natural logarithm of the centroid size was also included in the PC analysis alongside the Procrustes data, so that size as well as shape was represented in the results (although an analysis of shape alone produced the same outcome). A further six landmarks were recorded from the incisors of the gnawing analyses (see Fig. 4). These were subjected to a separate GMM analysis to investigate the effect of gape angle on the deformation experienced by the teeth. Analysis of variance (anova) and Student's t-tests, implemented in past v1.93 (Hammer et al. 2001) were used to test for significant differences between mean deformations experienced under different conditions.
Fig. 3.
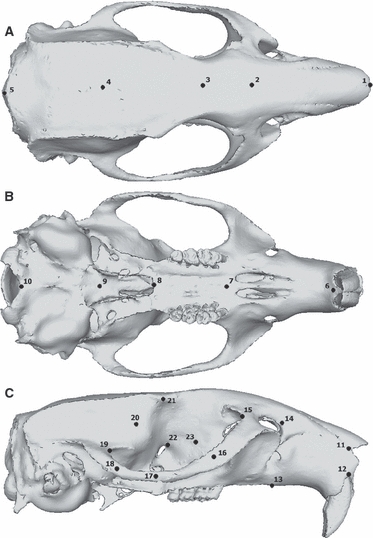
Landmarks used in GMM analysis of skull deformations as shown on reconstruction of rat skull in (A) dorsal, (B) ventral and (C) lateral view. 1, anteriormost point on internasal suture; 2, midpoint between anterior roots of zygomatic arch; 3, midpoint between medialmost points on orbital margins; 4, midpoint between temporo-mandibular joints; 5 posteriormost point on dorsal midline; 6, midpoint between ventral margins of incisal alveoli; 7, midpoint between anteriormost points of first cheek teeth; 8, posteriormost midline point on palatine; 9, midpoint between posterior margin of pterygoid flanges; 10, inferiormost point on margin of foramen magnum; 11, anteriormost point on naso-frontal suture; 12, dorsalmost point on incisal alveolar margin; 13, midpoint between incisor and first cheek tooth on ventral rostral margin; 14, postero-dorsal extremity of rostrum; 15, anteriormost point on orbital margin; 16, midpoint between 15 and 17; 17, ventralmost point on zygomatic arch; 18, midpoint between 17 and 19; 19, posteriormost point on orbital margin; 20, midpoint between 19 and 21; 21, posteriormost point on dorsal orbital margin; 22, antero-dorsal point on margin of orbital foramen; 23, midpoint of line running from dorsal apex of orbit to anterior margin of M2. Landmarks 11–23 recorded on both sides of skull.
Fig. 4.
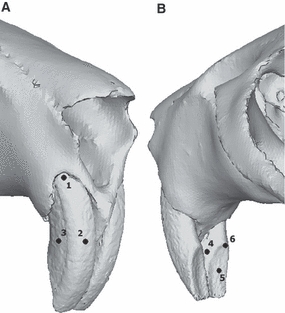
Landmarks used in GMM analysis of incisor deformation as shown on rat incisors in (A) anterior and (B) posterior view. 1, dorsalmost point of anterior surface; 2, midpoint of anterior surface; 3, midpoint of lateral surface; 4, midpoint of medial surface; 5, midpoint of basal surface; 6, dorsalmost point of basal surface.
Results
Analysis of variation in skull morphology
The results of the GMM analysis on all 23 rodents allowed the ‘most average’ individual of each rodent species to be determined. The percentage of total variance accounted for by each principal component is given in Table 1. The plot of the first two principal components of the GMM for all 23 rodents together is shown in Fig. 5. It can be seen that the individuals separate clearly into three groups: squirrels, rats and guinea pigs, showing that interspecific morphological variation is much greater than intraspecific variation in this sample. This is confirmed by anova, which demonstrates a statistically significant difference (P<0.001) between guinea pigs, rats and squirrels in this analysis. Examining the GMM analyses of each species individually, it can be seen that the first two principal components account for over 50% variation in each case (Table 1). In these individual analyses, the specimen closest to the origin of the plot could be determined, using Procrustes distances. This specimen was deemed to be closest to the mean form of the sample and was used in subsequent model construction and analyses. The FE models of these specimens were then loaded and assigned material properties to simulate the analyses outlined in Table S2.
Table 1.
Percentage of total variance accounted for by each principal component in a GMM analysis of 43 cranial landmarks recorded from 23 rodent individuals
| All rodents | Squirrels | Guinea pigs | Rats | |
|---|---|---|---|---|
| PC1 | 59.67 | 36.61 | 30.71 | 40.52 |
| PC2 | 30.77 | 19.57 | 24.93 | 17.46 |
| PC3 | 1.94 | 16.62 | 15.29 | 12.68 |
| PC4 | 1.28 | 12.09 | 12.20 | 10.51 |
Fig. 5.
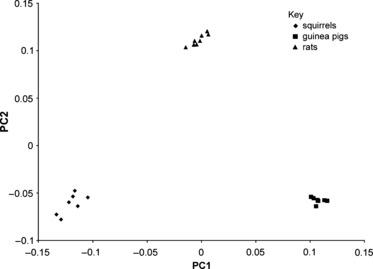
The first two principal components from a GMM analysis of cranial landmarks in all 23 rodents.
Analysis of skull deformations
Figures 6–8 shows the maximum principal strain distributions across the three models in three sample analyses: biting at the incisors, bilateral biting at M1 and unilateral biting at M3, all with a Young's modulus of bone of 10 GPa. Regions of the skull experiencing high strain during these bites are the zygomatic arch, the rostrum and the orbit. It was thus from these areas that the majority of landmarks to be used in the sensitivity analyses were recorded, although a number of midline landmarks were also taken to reflect general skull shape (see Fig. 3). Although these are just three sample analyses from the 130 conducted for each rodent model, some general patterns can be determined. As might be expected, the rostrum experiences high strains (particularly along its ventral margin) during incisor gnawing, but very low strains during molar chewing. The unilateral bite on the third molar generates a region of high strain in the dorsal temporal region immediately posterior to the orbit. This appears to be a product of both the unilateral nature of the bite and its mesiodistal position along the tooth row. The orbit is highly strained in incisor and M3 bites, but less so as a result of the M1 bite. Overall, the rat skull appears to be experiencing the highest strains and the guinea pig the lowest.
Fig. 6.
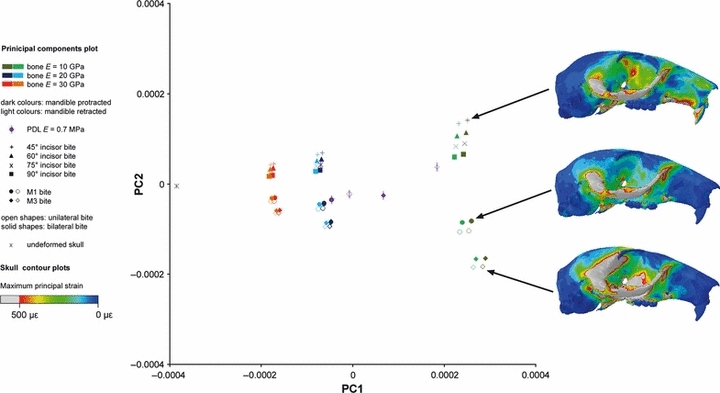
The first two principal components from the GMM analysis of 36 cranial landmarks in the squirrel. Maximum principal strains across the skull shown for three example analyses of incisor, M1 and M3 biting.
Fig. 8.
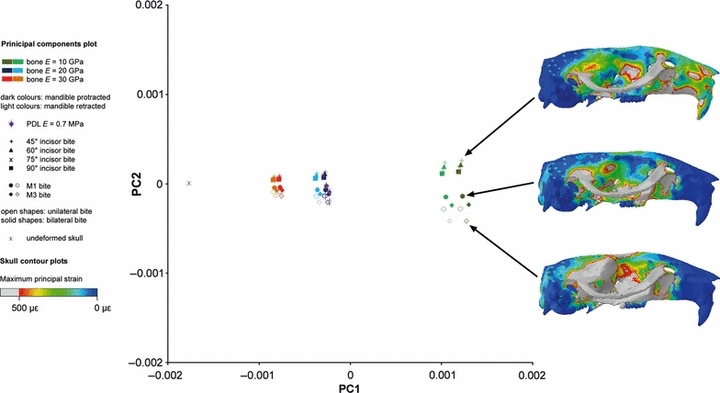
The first two principal components from the GMM analysis of 36 cranial landmarks in the rat. Maximum principal strains across the skull shown for three example analyses of incisor, M1 and M3 biting.
A GMM analysis of all FEAs for all three rodent species shows that variations in form due to deformations are miniscule compared to those resulting from underlying, unloaded morphological differences seen amongst the species studied. This is reflected in Table 2, where it can be seen that virtually all (> 99.99%) of the variation is accounted for by the first two principal components.
Table 2.
Percentage of total variance accounted for by each principal component in a GMM analysis of 36 cranial landmarks recorded from 130 analyses per model
| All rodents | Squirrel | Guinea pig | Rat | |
|---|---|---|---|---|
| PC1 | 64.51 | 78.22 | 55.74 | 95.65 |
| PC2 | 35.49 | 15.16 | 37.29 | 3.44 |
| PC3 | 0.00 | 4.94 | 5.73 | 0.74 |
| PC4 | 0.00 | 1.17 | 0.53 | 0.08 |
The form deformations analysed individually for the squirrel, rat and guinea pig models are shown in Figs 6–8, which include results for the variation of material properties, bite position and mandible position. The first two principal components account for over 90% of the variation in all three species (see Table 2), so only these two components have been shown here. It is notable that the vast majority of the variance is accounted for by the first principal component in the rat, whereas there is a much more even split between the first two components in the guinea pig. The second principal component accounts for around 37% of the variation in Cavia, compared to just 3% in Rattus. The squirrel sits between these two extremes with 15% of the variation on the second component. These differences in the distribution of variance across the principal components are clearly illustrated in Figs 6–8. In the rat and squirrel, all the analyses plot along lines parallel to the axes, whereas the guinea pig incisor analyses, while showing a similar pattern, are plotted along lines obliquely angled to the axes.
For each species, the variable that has the greatest effect on deformation of the skull is the elastic property of the bone. It can be seen in Figs 6–8 that the analyses group into three bands (mostly along the first principal component), representing bone with a Young's modulus of 10, 20 and 30 GPa (shown as green, blue and red points, respectively). The mean PC1 scores of these three bands representing the three values for bone stiffness were shown to be highly significantly different (P<0.001) in an anova test. Analyses with the stiffest bone, i.e. E = 30 GPa, deform the least and thus plot closest to the undeformed model. Analyses with the most flexible bone are seen at the greatest distance from the original skull. The distance between each analysis and the undeformed skull is known as the form distance and is a combination of the Procrustes distance and the log centroid size. Form distances and the Young's modulus of bone are inversely related, so that if the Young's modulus is halved, form distance doubles (this can be confirmed from the GMM plots). Analyses that differ only in the Young's modulus of bone show differences in strain magnitudes, not the pattern of strains across the skull, and sit on a linear trajectory that also includes the unloaded model. Hence, the principal components plots (Figs 6–8) all show a spreading, fan-like pattern in which analyses with a Young's modulus of bone of 30 GPa are tightly clustered close to the undeformed skull, and analyses with bone E of 10 GPa are more widely spaced at a greater distance. Because of this, the example maximum principal strain contour plots displayed in Figs 6–8 have been selected from separate trajectories, i.e. they differ in the position of the bite rather than the stiffness of the bone.
The second most important variable in terms of skull deformation is bite position. Within the three bands on each plot, the analyses separate clearly into incisor bite, unilateral M1 bite, bilateral M1 bite, unilateral M3 bite and bilateral M3 bite, with the incisor bite being quite distinct from the four molar bites. The separation between bite positions is not significant along the first principal component but is highly significant along the second component (P<0.001). In all three rodents, the bilateral bite at M1 is the most similar to the incisor bites and to the undeformed skull, and the unilateral bite at M3 is the furthest from them. In the squirrel, the molar bites form two clear groups representing M1 bites and M3 bites (circles and diamonds, respectively, in Figs 6–8), so that the pattern of molar bites in increasing distance from the undeformed skull is bilateral M1, unilateral M1, bilateral M3 and unilateral M3 (Fig. 6). This pattern is replicated in the guinea pig, although the clustering of M1 and M3 bites is not seen (Fig. 7). In fact, the unilateral M1 and bilateral M3 bites are very similar in this species. In rats, the pattern is altered to bilateral M1, bilateral M3, unilateral M1 and unilateral M3 (Fig. 8), so that the analyses are grouped into bilateral (solid shapes) and unilateral bites (open shapes). Within the incisor bites, there is a division into four groups representing the four different angles of bite at the incisor. In all three rodents, gnawing at 90° (squares) to the occlusal plane is most similar to molar biting and to the unloaded skull, whereas gnaws at 45° (+ crosses) are differ the most from mastication in terms of the skull deformations produced. In squirrels and rats, the four bite angles are separated along the second principal component, whereas in guinea pigs the axis of variation is oblique to both PC1 and PC2. Although the distinction between the incisor bite angles is obvious visually (at least within those analyses in which the Young's modulus of bone is 10 GPa), there is no statistically significant difference between them when subjected to an anova.
Fig. 7.
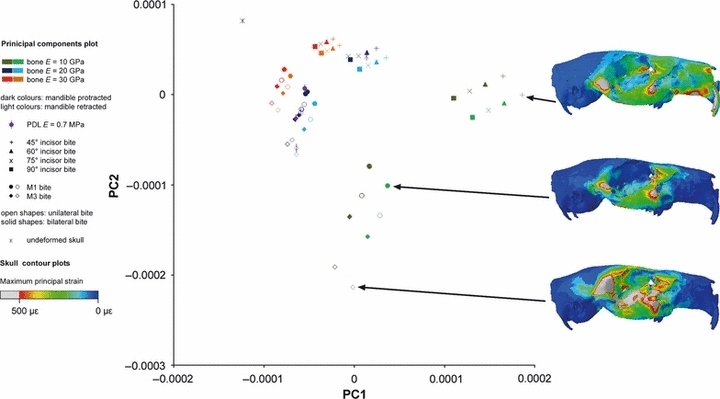
The first two principal components from the GMM analysis of 36 cranial landmarks in the guinea pig. Maximum principal strains across the skull shown for three example analyses of incisor, M1 and M3 biting.
The effect of the mandibular propaliny is shown clearly in Figs 6–8, in which the darker colours represent analyses in which the mandible was protracted and the lighter colours indicate analyses with a retracted mandible. Variation in the position of the mandible is seen along the same axis as variation in the Young's modulus of bone – for the rat and squirrel this is the first principal component, for the guinea pig it is an axis oblique to both the first and second principal components. The difference in deformation between the two mandibular positions is relatively small compared to the difference seen when changing the bone stiffness by 10 GPa, so the three bands representing the three input values for the Young's modulus of bone are still clearly visible. This variable also reveals a difference between the guinea pig model and the squirrel and rat models. Retraction of the mandible in the squirrel and rat decreases the form distance between the loaded and unloaded models, i.e. deformation is reduced, whereas retraction of the guinea pig mandible increases the form distance between the loaded and unloaded models, i.e. there is an increase in deformation. The difference between the analyses with a protracted and a retracted mandible was not significant over the whole dataset, but a significant difference in PC1 scores was found in the rat (P<0.001) and squirrel (P<0.05) models when the analyses were divided into three groups based on the Young's modulus of bone and subjected to separate t-tests.
The results of varying the Young's modulus of the periodontal ligament are somewhat unusual and have been displayed in purple and with a vertical line through the symbol in Figs 6–8 for ease of visualization. Very little difference in deformation pattern was found when the Young's modulus was varied from 50 to 1750 MPa. However, in all three rodents, the skull deformations produced by analyses in which the E value of PDL is 0.7 MPa are clearly separated from analyses with greater values for PDL stiffness. This effect is particularly noticeable in the squirrel model loaded to simulate biting at the molars, in which the analyses with low values of PDL stiffness are found at some distance from the corresponding analyses with higher PDL E values (Fig. 6). Furthermore, the impact of low Young's modulus on the deformation pattern was not consistent across bite positions or across the three rodents. Low PDL stiffness has the most impact on bilateral molar bites in the rat model, M3 bites in the squirrel model, and in the guinea pig model; the unilateral M3 bite and the incisor bites are the most affected. However, on further inspection of the squirrel model results with low PDL Young's modulus, it was noticed that the loaded molar was apparently being displaced through the bone, which is clearly an unrealistic outcome. Therefore, it was concluded that the strange results generated for low PDL Young's modulus (in the squirrel at least) were erroneous and possibly due to an inability of the software to cope with such a wide disparity (five orders of magnitude) between the PDL and bone stiffness values. This behaviour was not seen with the higher PDL values, or in any of the guinea pig and rat analyses.
The other variables studied in this analysis – material properties of the incisor enamel, dentine, pulp cavity, molar teeth and the periodontal ligament – are relatively unimportant factors affecting deformation of the skull compared to bone stiffness, bite position and lower jaw position. The individual analyses representing these variables cannot be distinguished from one another in Figs 6–8, and no statistically significant difference was found between them.
Analysis of incisor deformations
To analyse deformation of the incisors under varying loading conditions, six landmarks were taken from the incisors in each model and subjected to a geometric morphometric analysis. In this study, only the angle of the bite at the incisor and the material properties of the enamel and dentine were varied, giving a total of 24 analyses per species (see Supporting Information Table S3). Again, the landmarks from the undeformed models were also included in the GMM. The results of the analysis of all three rodents are shown in Table 3. As before, variations in form due to species differences completely overwhelm those resulting from variation in input parameters, and almost all the variation is accounted for by the first two principal components. Figures 9–11 show the plots of the first two principal components for the analyses of each rodent separately. The maximum principal strain contour plots have also been shown for four sample analyses, representing the four bite angles, for each rodent. Table 3 gives the percentage of variance contained within each principal component. In this analysis, the first principal component covers over 80% of the variation in all three rodents. However, in a reversal of the situation seen in the analysis of skull deformations, here it is the guinea pig that is most dominated by the first component – 99.5% of variation is seen here – and it is the rat that has the greatest amount of variance accounted for by the second component (15%).
Table 3.
Percentage of total variance accounted for by each principal component in a GMM analysis of six incisor landmarks recorded from 24 analyses per model
| All rodents | Squirrel | Guinea pig | Rat | |
|---|---|---|---|---|
| PC1 | 58.13 | 87.72 | 99.54 | 81.99 |
| PC2 | 41.87 | 7.51 | 0.38 | 15.30 |
| PC3 | 0.00 | 1.43 | 0.04 | 1.76 |
| PC4 | 0.00 | 1.07 | 0.01 | 0.41 |
Fig. 9.
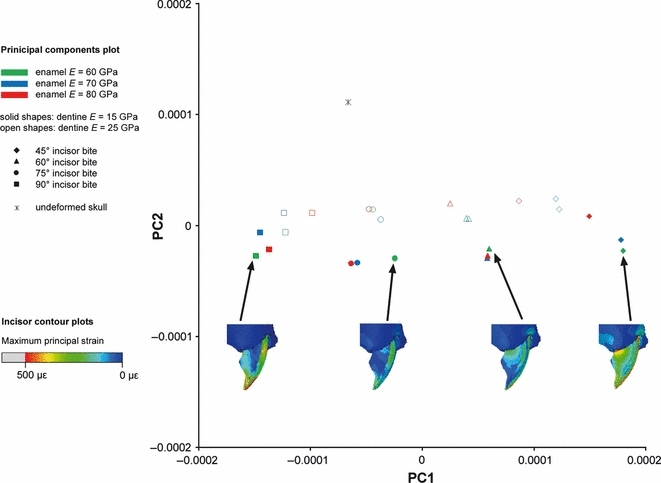
The first two principal components from the GMM analysis of six incisor landmarks in the squirrel. Maximum principal strains across the incisor shown for four sample analyses of biting at 45°, 60°, 75° and 90° to the occlusal plane.
Fig. 11.
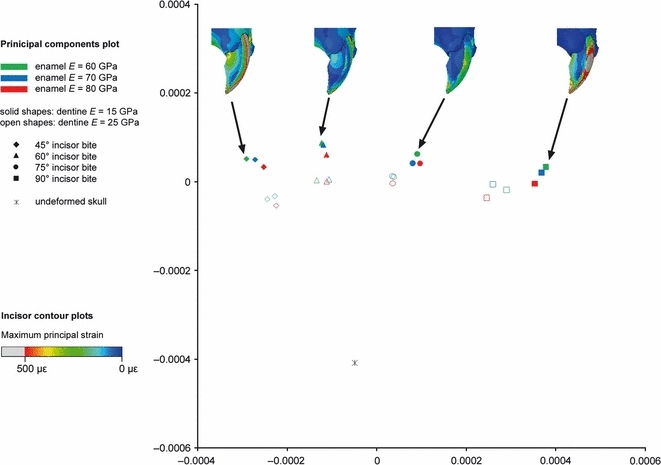
The first two principal components from the GMM analysis of six incisor landmarks in the rat. Maximum principal strains across the incisor shown for four example analyses of biting at 45°, 60°, 75° and 90° to the occlusal plane.
It can be seen from Figs 9–11 that bite angle is the most important variable affecting deformation of the incisors. The four bite angles analysed (90°, 75°, 60° and 45° to the occlusal plane) form four distinct groups along the first principal component. The difference between the means of these groups is highly significant (P<0.001). It is particularly interesting to note that the relationship of the undeformed model to the four groups representing different bite angles varies between the three rodent species. In the guinea pig, biting at 90° and 75° results in distinctly less deformation than biting at smaller angles to the occlusal plane (Fig. 10). In comparison, squirrels and rats appear to be able to gnaw at a much greater range of angles (60°–90° in squirrels, 45°–75° in rats), without much difference in the amount of deformation (Figs 9 and 11). This can be seen from both the form distances and the maximum principal strain contour plots.
Fig. 10.
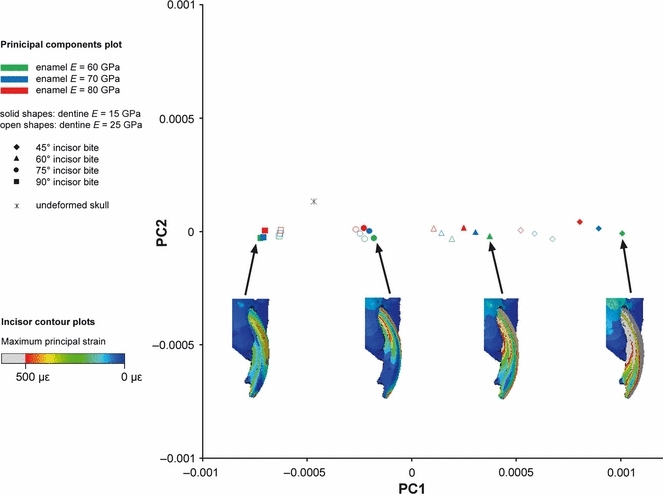
The first two principal components from the GMM analysis of six incisor landmarks in the guinea pig. Maximum principal strains across the incisor shown for four example analyses of biting at 45°, 60°, 75° and 90° to the occlusal plane.
Within each bite angle, the analyses are separated by the Young's modulus of the enamel and the dentine. As might be expected, the more flexible the enamel or dentine, the greater the deformation, and hence the greater the distance of the analysis from the original incisor on the principal components plot. In the rats and squirrels, variation in the dentine stiffness causes separation of the analyses along the second principal component, which is statistically significant (P<0.001) in an anova test. Enamel stiffness is the least important variable for these two rodents and does not produce statistically significant separation along either of the first two principal components. In contrast, in the guinea pig it is the variation in enamel stiffness that separates the analyses along PC2, and dentine stiffness is the least important variable.
Discussion
The results of this morphometric analysis show that, of the parameters varied in this analysis, the material properties of the bone are the most important variables when modelling deformation in the skull generated by feeding. It can be seen that a change of 10 GPa in Young's modulus can produce a greater change in the deformed skull form than a change in bite position. Although this is a relatively large variation in modulus, it does demonstrate the importance of using accurate material properties in finite element models, as relatively small changes can produce significant variations in the results. However, as mentioned above, changes in Young's modulus only produce changes in the strain magnitudes, not the strain patterns seen across the skull (as also noted by Strait et al. 2005). Therefore, although accurate knowledge of bone material properties is vital for predicting strain values, it is not so important if comparison of strain patterns is the desired outcome of the analysis. It should be noted that the models considered here assumed isotropic material properties, whereas in reality there will almost certainly be some anisotropy in the bone (Peterson & Dechow, 2003; Strait et al. 2005). It is currently not possible to measure these directional variations in skulls of this size, but in any case, it seems unlikely that the overall sensitivity of the results to the material properties will be significantly different.
It has also been demonstrated that bite position can have a large effect on deformation patterns in the skull, although not nearly as much as bone material properties, given the high percentage of the variance seen on the first principal component. Incisor bites are always well differentiated from molar bites on the principal component plots. This is unsurprising given the wide diastema between the incisors and cheek teeth. It can be seen from the maximum principal strain plots in Figs 6–8 that the rostrum experiences high strains during incisor gnawing but remains relatively unloaded during molar biting, and this is bound to produce large differences in the pattern of deformation. The four molar bites modelled here are also easily distinguishable on the principal component plots; however, they do not have the same relationship to each other in the three models. In the squirrel and guinea pig, all bites on the same tooth produce similar deformation patterns, whether they are bilateral or unilateral. This is not the case in rats, in which bilateral bites on different teeth are more similar than a bilateral and a unilateral bite on the same tooth. This may be attributable to a slightly shorter molar tooth row in the rat, in which the distance between the first and third molars is around 9.5% of the total skull length as opposed to about 13% in the squirrel and the guinea pig. A further influence may be the geometry of the skull and the positioning of the teeth. The rat molars are located such that any vertical force on them, whether it is on the first or third molar, will tend to propagate stress directly upwards into the orbit (Fig. 8). In the squirrel and guinea pig, force will also be directed into the orbit from the third molar, but the morphology of the skull means that forces from the first molar remain localized around the root of the zygomatic arch and are not transmitted to the orbit (Figs 6 and 7). Thus the deformations generated by an M1 bite are fairly similar to those produced by an M3 bite in the rat, but are quite distinct in the squirrel and guinea pig.
The effect of varying the direction of pull of the muscle forces is highlighted in this study. Rodents are notable amongst mammals in having two distinct positions of the mandible at which biting can take place: a protracted orientation with the incisors in occlusion and a retracted orientation with the molars in occlusion. Although the absolute distance between the two arrangements is relatively small (2–3 mm displacement), it has been shown here that the corresponding change in the orientation of the masticatory muscles can make a noticeable difference to the results of an FE analysis. The most striking difference in the analyses presented here is seen between the guinea pig, and the squirrel and rat. Retraction of the mandible in the squirrel and rat leads to a reduction in the degree of deformation experienced by the skull, whereas in the guinea pig it is protraction of the mandible that reduces skull deformation. However, it should be noted that this is a hypothetical distinction, as rodents can only accomplish incisor gnawing by protracting the mandible and can only chew at the molars by retracting it. The options of chewing with a protracted lower jaw or gnawing with a retracted lower jaw are not available. On examination of the Procrustes distances between both protracted-mandible gnawing and retracted-mandible chewing and the undeformed skull, it can be seen that the amount of skull deformation is very similar in each case, for any given Young's modulus of bone. Therefore, the results indicate that accurate modelling of muscle orientations is important in FEA, and where changes in the muscle pull directions occur due to movement of the mandible (as in many groups of amniotes; Reilly et al. 2001), these should be incorporated into the model.
The elastic properties of the periodontal ligament in cranial and mandibular FE models have been studied in previous research with little consensus so far as to the extent of the influence of the PDL on strain distributions (Marinescu et al. 2005; Gröning et al. 2011; Panagiotopoulou et al. 2011; Wood et al. 2011). This study indicates that changing the Young's modulus of PDL between 50 and 1750 MPa – the highest E value for PDL in the scientific literature (Goel et al. 1992), as reported by Rees & Jacobsen (1997)– has very little effect on the overall deformation of the rodent skull, although there were of course local effects around the alveoli of the teeth. This is in agreement with previously conducted sensitivity analyses of the properties of PDL in a primate cranium (Wood et al. 2011). However, the results of this analysis are somewhat confounded by the unusual and inconsistent deformations experienced by the models with very low Young's modulus of the PDL (E = 0.7 MPa), and it is hypothesized that these deformations may be erroneous, a result of the large disparity (several orders of magnitude) between the Young's modulus of the PDL and the surrounding bone. It is clear that the material properties of the PDL are a highly contentious issue and require further investigation, particularly with regard to very low values of Young's modulus.
The results of the analysis of incisor deformation show that the guinea pig incisors deform least during bites which are perpendicular to the occlusal plane. This is in contrast to rats and squirrels, in which incisal deformation is much more consistent over a large range of bite angles. This suggests that gnawing in guinea pigs may be limited to quite narrow gape angles, whereas rats and squirrels are capable of efficient gnawing at both wide and narrow gapes. This would allow them to feed on food items of different sizes, a finding that is consistent with the known diets of the rodents (Nowak, 1999). Rats and squirrels eat a much greater proportion of hard foods (nuts and seeds) that require gnawing at the incisors, whereas guinea pigs rely more on vegetation, which tends to be chewed at the molars and does not require a wide gape for ingestion. The varying importance of the material properties of the enamel and dentine in the three rodents reflects the composition of the incisors in these three species. In the rat and squirrel, the dentine forms a large part of the incisor (approximately 70%, as measured in the FE models constructed for this study) compared to the enamel, and so it has a greater influence on the deformation of the incisor during biting. In guinea pigs, the dentine is somewhat reduced (around 50%) and it is the enamel that is the more important variable in determining deformation patterns.
Concluding remarks
It has been demonstrated that, of the input parameters studied here, the variables with the greatest influence on the overall deformation predicted by a finite element analysis of three representative rodent skulls are bone stiffness and, to a lesser extent, bite position, muscle orientation and bite angle. It is clearly important to model these variables as accurately as possible in FE models to have the highest possible confidence in the results. Significant variations in material properties were considered and yet the properties of the tooth materials, enamel, dentine and pulp appear to be relatively unimportant in these analyses, despite the large size of the incisors in rodents, and can be varied widely with little effect on the overall pattern of deformation across the skull. Nevertheless, these variables can have a substantial influence locally and, of course, are paramount when studying deformation in the teeth themselves. It should be noted that overall deformation of the skull is being represented by a single point in the GMM analyses presented here, and although the relative distortions of the different analyses can be seen, no inferences can be drawn on the differing distributions of the deformations. Furthermore, the loads applied to the models are non-physiological, i.e. all muscles are contracting fully in each bite. Variation in the relative muscle forces between the sensitivity analyses (for example, to optimize for bite force) could produce different deformation distributions. These caveats notwithstanding, this study, although limited in its scope to three species of rodent, contributes to a wider body of evidence suggesting that the elastic modulus of bone is one of the key variables for determining the outcome of FE analyses (Strait et al. 2005; Bright & Rayfield, 2011; Reed et al. 2011). Using the results of this analysis to inform our choice of input parameters, we now intend to investigate the biological significance of the results of the FE analyses under certain loading regimes in the squirrel, guinea pig and rat.
Acknowledgments
The authors thank Sue Taft, Department of Engineering, University of Hull for microCT imaging of the rodent heads. Thanks are also due to Jen Bright, University of Bristol and Daniel Nieto, Altair Engineering for assistance with modelling software. We are grateful for many helpful comments on the manuscript from Paul O'Higgins, Hull-York Medical School. This work was supported by the Natural Environmental Research Council (NERC grant NE/G001952/1).
Supporting Information
Additional Supporting Information may be found in the online version of this article:
Table S1. Cranial landmarks used to determine ‘average’ individuals.
Table S2. FE analyses solved for each rodent model, for analysis of skull deformations.
Table S3. FE analyses solved for each rodent model, for analysis of incisor deformations.
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
References
- Adams DC, Rohlf FJ, Slice DE. Geometric morphometrics: ten years of progress following the ‘revolution’. Ital J Zool. 2004;71:5–16. [Google Scholar]
- Adkins RM, Walton AH, Honeycutt RL. Higher-level systematics of rodents and divergence time estimates based on two congruent nuclear genes. Mol Phylogenet Evol. 2003;26:409–420. doi: 10.1016/s1055-7903(02)00304-4. [DOI] [PubMed] [Google Scholar]
- Becht G. Comparative biologic-anatomical researches on mastication in some mammals. Proc Kon Ned Akad Wet, Ser C. 1953;56:508–527. [Google Scholar]
- Blanga-Kanfi S, Miranda H, Penn O, et al. Rodent phylogeny revised: analysis of six nuclear genes from all major rodent clades. BMC Evol Biol. 2009;9:71. doi: 10.1186/1471-2148-9-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brandt JF. Untersuchungen über die craniologischen Entwicklungsstufen und Classification der Nager der Jetzwelt. Mém Acad Imp Sci St Pétersbourg, Sér. 1855;6(9):1–365. [Google Scholar]
- Bright JA, Rayfield EJ. Sensitivity and ex vivo validation of finite element models of the domestic pig cranium. J Anat. 2011;219:456–471. doi: 10.1111/j.1469-7580.2011.01408.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byrd KE. Mandibular movement and muscle activity during mastication in the guinea pig (Cavia porcellus) J Morphol. 1981;170:147–169. doi: 10.1002/jmor.1051700203. [DOI] [PubMed] [Google Scholar]
- Cox PG, Jeffery N. Reviewing the jaw-closing musculature in squirrels, rats and guinea pigs with contrast-enhanced microCT. Anat Rec Part A. 2011;294:915–928. doi: 10.1002/ar.21381. [DOI] [PubMed] [Google Scholar]
- Druzinsky RE. Functional anatomy of incisal biting in Aplodontia rufa and sciuromorph rodents – Part 2: sciuromorphy is efficacious for production of force at the incisors. Cells Tissues Organs. 2010;192:50–63. doi: 10.1159/000284930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumont ER, Piccirillo J, Grosse IR. Finite-element analysis of biting behavior and bone stress in the facial skeletons of bats. Anat Rec Part A. 2005;283A:319–330. doi: 10.1002/ar.a.20165. [DOI] [PubMed] [Google Scholar]
- Dumont ER, Davis JL, Grosse IR, et al. Finite element analysis of performance in the skulls of marmosets and tamarins. J Anat. 2010;218:151–162. doi: 10.1111/j.1469-7580.2010.01247.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagan MJ, Julian S, Siddall DJ, et al. Patient-specific spine models. Part 1: finite element analysis of the lumbar intervertebral disc – a material sensitivity study. Proc Instn Mech Eng H. 2002;216:299–314. doi: 10.1243/09544110260216577. [DOI] [PubMed] [Google Scholar]
- Freeman PW, Lemen CA. Measuring bite force in small mammals with a piezo-resistive sensor. J Mammal. 2008;89:513–517. [Google Scholar]
- Goel VK, Khera SC, Gurusami S, et al. Effect of cavity depth on stresses in a restored tooth. J Prosthet Dent. 1992;67:174–183. doi: 10.1016/0022-3913(92)90449-k. [DOI] [PubMed] [Google Scholar]
- Gorniak GC. Feeding in golden hamsters, Mesocricetus auratus. J Morphol. 1977;154:427–458. doi: 10.1002/jmor.1051540305. [DOI] [PubMed] [Google Scholar]
- Gröning F, Fagan MJ, O'Higgins P. The effects of the periodontal ligament on mandibular stiffness: a study combining finite element analysis and geometric morphometrics. J Biomech. 2011;44:1304–1312. doi: 10.1016/j.jbiomech.2011.01.008. [DOI] [PubMed] [Google Scholar]
- Hammer Ø, Harper DAT, Ryan PD. PAST: paleontological statistics software package for education and data analysis. Palaeontol Electronica. 2001;4:9. [Google Scholar]
- Hautier L, Clavel J, Lazzari V, et al. Biomechanical changes and remodeling of the masticatory apparatus during mammalian evolution: the case of the Issiodoromyinae (Rodentia) Palaios. 2010;25:6–13. [Google Scholar]
- Hiiemae K. The structure and function of jaw muscles in rat (Rattus norvegicus L.). III. The mechanics of the muscles. Zool J Linn Soc. 1971;50:111–132. [Google Scholar]
- Hiiemae K, Ardran GM. A cinefluorographic study of mandibular movement during feeding in the rat (Rattus norvegicus) J Zool. 1968;154:139–154. [Google Scholar]
- Jeffery NS, Stephenson R, Gallagher JA, et al. Micro-computed tomography with iodine staining resolves the arrangement of muscle fibres. J Biomech. 2011;44:189–192. doi: 10.1016/j.jbiomech.2010.08.027. [DOI] [PubMed] [Google Scholar]
- Kupczik K, Dobson CA, Fagan MJ, et al. Assessing mechanical function of the zygomatic region in macaques: validation and sensitivity testing of finite element models. J Anat. 2007;210:41–53. doi: 10.1111/j.1469-7580.2006.00662.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marinescu R, Daegling DJ, Rapoff AJ. Finite-element modeling of the anthropoid mandible: the effects of altered boundary conditions. Anat Rec Part A. 2005;283A:300–309. doi: 10.1002/ar.a.20166. [DOI] [PubMed] [Google Scholar]
- McHenry CR, Wroe S, Clausen PD, et al. Supermodeled sabercat, predatory behavior in Smilodon fatalis revealed by high-resolution 3D computer simulation. Proc Natl Acad Sci U S A. 2007;140:16010–16015. doi: 10.1073/pnas.0706086104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moazen M, Curtis N, Evans SE, et al. Biomechanical assessment of evolutionary changes in the lepidosaurian skull. Proc Natl Acad Sci U S A. 2009;20:8273–8277. doi: 10.1073/pnas.0813156106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno K, Wroe S, Clausen P, et al. Cranial performance in the Komodo dragon (Varanus komodoensis) as revealed by high-resolution 3-D finite element analysis. J Anat. 2008;212:736–746. doi: 10.1111/j.1469-7580.2008.00899.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nies M, Ro JY. Bite force measurement in awake rats. Brain Res Protoc. 2004;12:180–185. doi: 10.1016/j.brainresprot.2003.11.003. [DOI] [PubMed] [Google Scholar]
- Nowak R. Walker's Mammals of the World. Baltimore: Johns Hopkins Press; 1999. [Google Scholar]
- O'Higgins P. The study of morphological variation in the hominid fossil record: biology, landmarks and geometry. J Anat. 2000;197:103–120. doi: 10.1046/j.1469-7580.2000.19710103.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Higgins P, Cobb SN, Fitton LC, et al. Combining geometric morphometrics and functional simulation: an emerging toolkit for virtual functional analyses. J Anat. 2011;218:3–15. doi: 10.1111/j.1469-7580.2010.01301.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivares AI, Verzi DH, Vassallo AI. Masticatory morphological diversity and chewing modes in South American caviomorph rodents (family Octodontidae) J Zool. 2004;263:167–177. [Google Scholar]
- Panagiotopoulou O, Kupczik K, Cobb SN. The mechanical function of the periodontal ligament in the macaque mandible: a validation and sensitivity study using finite element analysis. J Anat. 2011;218:75–86. doi: 10.1111/j.1469-7580.2010.01257.x. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Peterson J, Dechow PC. Material properties of the human cranial vault and zygoma. Anat Rec Part A. 2003;274A:785–797. doi: 10.1002/ar.a.10096. [DOI] [PubMed] [Google Scholar]
- Rayfield EJ. Cranial mechanics and feeding in Tyrannosaurus rex. Proc R Soc Lond B. 2004;271:1451–1459. doi: 10.1098/rspb.2004.2755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rayfield EJ. Aspects of comparative cranial mechanics in the theropod dinosaurs Coelophysis, Allosaurus and Tyrannosaurus. Zool J Linn Soc. 2005;144:309–316. [Google Scholar]
- Reed DA, Porro LB, Iriarte-Diaz J, et al. The impact of bone and suture material properties on mandibular function in Alligator mississippiensis: testing theoretical phenotypes with finite element analysis. J Anat. 2011;218:59–74. doi: 10.1111/j.1469-7580.2010.01319.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees JS, Jacobsen PH. Elastic modulus of the periodontal ligament. Biomaterials. 1997;18:995–999. doi: 10.1016/s0142-9612(97)00021-5. [DOI] [PubMed] [Google Scholar]
- Reilly SM, McBrayer LD, White TD. Prey processing in amniotes: biomechanical and behavioral patterns of food reduction. Comp Biochem Physiol Part A. 2001;128:397–415. doi: 10.1016/s1095-6433(00)00326-3. [DOI] [PubMed] [Google Scholar]
- Robins MW. Biting loads generated by the laboratory rat. Arch Oral Biol. 1977;22:43–47. doi: 10.1016/0003-9969(77)90138-8. [DOI] [PubMed] [Google Scholar]
- Ross CF, Patel BA, Slice DE, et al. Modeling masticatory muscle force in finite element analysis: sensitivity analysis using principal coordinates analysis. Anat Rec Part A. 2005;283A:288–299. doi: 10.1002/ar.a.20170. [DOI] [PubMed] [Google Scholar]
- Satoh K. Comparative functional morphology of mandibular forward movement during mastication of two murid rodents, Apodemus speciosus (Murinae) and Clethrionomys rufocanus (Arvicolinae) J Morphol. 1997;231:131–142. doi: 10.1002/(SICI)1097-4687(199702)231:2<131::AID-JMOR2>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- Satoh K. Balancing function of the masticatory muscles during incisal biting in two murid rodents, Apodemus speciosus and Clethrionomys rufocanus. J Morphol. 1998;236:49–56. doi: 10.1002/(SICI)1097-4687(199804)236:1<49::AID-JMOR3>3.0.CO;2-J. [DOI] [PubMed] [Google Scholar]
- Satoh K. Mechanical advantage of area of origin for the external pterygoid in two murid rodents, Apodemus speciosus and Clethrionomys rufocanus. J Morphol. 1999;240:1–14. doi: 10.1002/(SICI)1097-4687(199904)240:1<1::AID-JMOR1>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Simpson GG. The principles of classification and a classification of mammals. Bull Am Mus Nat Hist. 1945;85:1–350. [Google Scholar]
- van Spronsen PH, Weijs WA, Valk J, et al. Comparisons of jaw-muscle bite-force cross-sections obtained by means of magnetic resonance imaging and high-resolution CT scanning. J Dent Res. 1989;68:1765–1770. doi: 10.1177/00220345890680120901. [DOI] [PubMed] [Google Scholar]
- Strait DS, Wang Q, Dechow PC, et al. Modeling elastic properties in finite element analysis: how much precision is needed to produce an accurate model? Anat Rec Part A. 2005;283A:275–287. doi: 10.1002/ar.a.20172. [DOI] [PubMed] [Google Scholar]
- Tanne K, Sakuda M, Burstone CJ. Three-dimensional finite element analysis for stress in the periodontal tissue by orthodontic forces. Am J Orthod Dentofacial Orthop. 1987;92:499–505. doi: 10.1016/0889-5406(87)90232-0. [DOI] [PubMed] [Google Scholar]
- Vassallo AI, Verzi DH. Patrones craneanos y modalidades de masticacion en roedores caviomorfos (Rodentia, Caviomorpha) Bol Soc Biol Concepc. 2001;72:145–151. [Google Scholar]
- Weijs WA, Dantuma R. Electromyography and mechanics of mastication in the albino rat. J Morphol. 1975;146:1–34. doi: 10.1002/jmor.1051460102. [DOI] [PubMed] [Google Scholar]
- Williams KR, Edmundson JT. Orthodontic tooth movement analysed by the finite element method. Biomaterials. 1984;5:347–351. doi: 10.1016/0142-9612(84)90033-4. [DOI] [PubMed] [Google Scholar]
- Wilson A. Linear and Non-linear Analysis of Orthodontic Tooth Movement. Swansea: University of Wales; 1991. PhD thesis. [Google Scholar]
- Wilson DE, Reeder DM. Mammal Species of the World. Baltimore: Johns Hopkins Press; 2005. [Google Scholar]
- Wood AE. Grades and clades among rodents. Evolution. 1965;19:115–130. [Google Scholar]
- Wood SA, Strait DS, Dumont ER, et al. The effects of modeling simplifications on craniofacial finite element models: the alveoli (tooth sockets) and periodontal ligaments. J Biomech. 2011;44:1831–1838. doi: 10.1016/j.jbiomech.2011.03.022. [DOI] [PubMed] [Google Scholar]
- Wroe S, Clausen P, McHenry C, et al. Computer simulation of feeding behaviour in the thylacine and dingo as a novel test for convergence and niche overlap. Proc R Soc Lond B. 2007;274:2819–2828. doi: 10.1098/rspb.2007.0906. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


