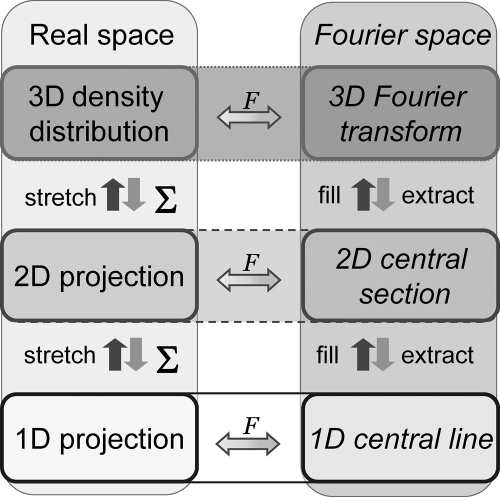
Figure 20.

Relationships between images and projections in real and Fourier space. The 3D structure can be projected onto planes to give 2D projections, which can in turn be projected in different directions to yield 1D (line) projections, indicated by the operator of summation ∑. The complete set of line projections is known as the Radon transform. A sinogram is a set of line projections of the 2D projection or a section of the 3D Radon transform. In the reverse direction, the set of line projections can be combined to reconstruct the 2D image and the set of 2D projections combined to reconstruct the 3D object, indicated by the operator of stretching. The image information can be equivalently represented in reciprocal space, in the form of Fourier amplitudes and phases (right column). Fourier transforms (F) of the 2D projections correspond to central sections of the 3D transform (extraction), and the line projections correspond to lines passing through the origin of Fourier space (central lines). Therefore, the object can also be reconstructed by combining (filling) the set of central sections into the 3D transform followed by inverse 3D Fourier transformation. Adapted with permission from ref (12). Copyright 2000 Cambridge University Press.