Facilitated Diffusion of Myoglobin and Creatine Kinase and Reaction-Diffusion Constraints of Aerobic Metabolism Under Steady State Conditions in Skeletal Muscle

Abstract

The roles of creatine kinase (CK) and myoglobin (Mb) on steady-state facilitated diffusion and temporal buffering of ATP and oxygen, respectively, are assessed within the context of a reaction-diffusion model of muscle energetics. Comparison of the reaction-diffusion model with experimental data from a wide range of muscle fibers shows that the experimentally observed skeletal muscle fibers are generally not limited by diffusion, and the model further indicates that while some muscle fibers operate near the edge of diffusion limitation, no detectable effects of Mb and CK on the effectiveness factor, a measure of diffusion constraints, are observed under steady-state conditions. However, CK had a significant effect on average ATP concentration over a wide range of rates and length scales within the reaction limited regime. The facilitated diffusion functions of Mb and CK become observable in the model for larger size cells with low mitochondrial volume fraction and for low boundary O₂ concentration and high ATP demand, where the fibers may be limited by diffusion. From the transient analysis it may be concluded that CK primarily functions to temporally buffer ATP as opposed to facilitating diffusion while Mb has a small temporal buffering effect on oxygen but does not play any significant role in steady state facilitated diffusion in skeletal muscle fibers under most physiologically relevant regions.

Introduction

The enhancement of the molecular transport of a solute by one or more carriers that reversibly bind with that solute, termed facilitated diffusion or carrier mediated transport, is important in a number of biological and bioengineering systems as well as in chemical separations processes (Noble et al., 1989). Two of the most important examples in biological systems involve the delivery of oxygen by hemoglobin or myoglobin (Mb) and the delivery of ATP by the phosphagen kinase system (Sweeney, 1994), e.g. creatine kinase (CK) in vertebrates and arginine kinase in some invertebrates. Both ATP and oxygen delivery are fundamental requirements in muscle energy metabolism, and while there is some debate on the degree to which facilitated transport functions, facilitated diffusion theory has long been invoked to explain the functions of CK (Meyer et al., 1984) and Mb (Wittenberg, 1959) to reduce diffusion limitations in muscle of ATP and O₂, respectively.

Most of the controversy regarding the CK system has centered on aspects of enzyme localization, metabolic compartmentation, and the details by which CK couples oxidative phosphorylation to ATP consumption. However, the notions that CK serves to both temporally buffer ATP during changes in ATP demand, where the CK builds up a large pool of rapidly diffusing phosphocreatine resulting in temporal buffering of ATP levels by reversible interconversion of creatine to phosphocreatine (Meyer et al., 1984), and to facilitate diffusion of ATP during steady state contraction, have been generally accepted features of this enzyme system, if not universally viewed as the principal functions in all cell types (Bessman and Geiger, 1981; Wallimann et al., 1992; Wyss and Kaddurah-Daouk, 2000; Dzeja and Terzic, 2003; Ingwall, 2004; Saks et al., 2008; Beard and Kushmerick, 2009). In contrast, Mb is thought to be exclusively soluble and therefore mobile in the cytoplasm. This mobility, coupled with rapid reversible binding of O₂, is suggested to cause Mb to act as a temporal buffer of O₂ during contraction-induced perfusion interruption and to function as a facilitator of O₂ diffusion during steady-state contraction (Wittenberg, 1959; Wittenberg and Wittenberg, 1989, 2003; Conley et al., 2000; Jürgens et al., 2000; Ordway and Garry, 2004). However, experimental measurements of the Mb diffusion coefficient (D) in muscle coupled with reaction-diffusion analyses suggest that the contribution of Mb facilitated diffusion in muscle contracting at steady-state is small (Jürgens et al., 1994; Papadopoulos et al., 1995; Lin et al., 2007b; Gros et al., 2010).

On the other hand, recent comparison of experimental observations of aerobic metabolism with computational reaction-diffusion analyses in skeletal muscle has shown that under steady state conditions muscle fibers in general are not greatly limited by diffusion, although some fibers operate near the transition region where diffusion limitations arise. Simply stated, muscles are under reaction control under most physiological conditions, although they may be diffusion limited at the extremes of their functional range (Locke and Kinsey, 2008; Jimenez et al., 2008, Dasika et al., 2011). In principle, diffusion limitations will become important as the diffusion distance (e.g., fiber size) or reaction rate (e.g., ATP turnover) increase, yet muscles generally operate under reaction-control even when the fibers are very large (Jimenez et al., 2008; Hardy et al., 2009) or rates of aerobic ATP turnover are very high (Locke and Kinsey, 2008; Kinsey et al., 2007, 2011). The enhancement in diffusion (offsetting the diffusional constraints) due to facilitated diffusion may not be important when the muscle cell function under chemical reaction control.

These observations therefore lead to the need to re-evaluate the functions of the phosphagen kinase and Mb systems in skeletal muscle for a wide range of animals, to test the assumption that facilitated diffusion is a major function during stead-state aerobic metabolism, and to determine the region of parameter space (e.g., cell size, metabolic demand, oxygen supply) where facilitated diffusion may play a predominant role. Previous mathematical modeling studies of facilitated diffusion in muscle have focused individually on either oxygen transport with Mb or ATP transport with the phosphagen kinase; to our knowledge analysis of facilitated transport in muscle where the simultaneous reaction and transport of both oxygen and ATP occur has not been reported. In addition, classical steady-state facilitated diffusion models typically consider solute transport across a finite domain, i.e. membrane, such that the adjoining boundaries have fixed concentrations of the solute (Al-Marzouqi et al,. 2002; Goddard et al., 1974; Jemaa and Noble, 1992; Schultz et al., 1974; Teramoto, 1994). Much effort has been devoted in such cases to determining enhancement factors that provide measures of the degree to which transport across the membrane is enhanced by the carrier. Such models may apply to transport across biological membranes or even in the blood stream, however, they generally over simplify the combined effects of the reversible binding reactions of the solute with the carrier and the irreversible consumption reactions of the solute, e.g. oxygen consumption by mitochondria or ATP consumption by ATPase, in addition to neglecting the coupling effects between ATP formation/consumption and oxygen consumption. Models that presuppose facilitated diffusion may be somewhat limited to the domain of applicability where facilitated diffusion occurs; more general models that include all appropriate chemical reactions, both reversible binding and irreversible consumption or formation, through all species continuity balances can be applicable over a broader range of parameter space.

The aim of the present study was therefore to analyze the effects of phosphagen kinase reactions like CK and the reversible binding of Mb to O₂ on the diffusion limitations of skeletal muscle fibers, taking advantage of the wide diversity of fiber size (diffusion distances) and aerobic capacity found in the animal kingdom in order to elucidate general principles of CK and Mb function. The reaction-diffusion model developed in our previous study (Dasika et al., 2011) incorporates a detailed description of oxidative phosphorylation in the mitochondria coupled to the intracellular ATPase reactions, and includes both CK (or arginine kinase) and Mb. In order to assess the roles of phosphagen kinases and Mb on the resulting effectiveness factor, i.e., the ratio of the observed rate in the presence of diffusion limitations to the ideal case in the absence of diffusion limitation, we compute this factor for cases a) with both CK and Mb, b) with CK and without Mb, c) without CK and with Mb, and d) without both CK and Mb. We compare the results to available experimental observations on a wide range of fiber types and assess the model as a function of metabolic demand, cell size, and oxygen supply in order to determine the conditions where diffusion control, and thus facilitated diffusion, may play important roles.

Modeling methods and formulation

Detailed aspects of the reaction-diffusion model used here are described in previous work (Dasika et al., 2011). In brief, we developed a simplified rate law for mitochondrial ATP production as a function of ADP, P_i, and O₂ based upon a published mechanism (Beard, 2005), and a 1-D reaction diffusion model with ATP, ADP, P_i, O₂, Mb, myoglobin-bound O₂ (MbO₂), creatine (Cr), and phosphocreatine (PCr) as metabolites. Mitochondria were assumed to be homogeneously distributed throughout the cell and volume averaging technique (Whitaker, 1999) was performed to account for contribution from all mitochondria in the cell. The species continuity equation for any species i is given by

$$\frac{\partial {\stackrel{⌢}{\text{C}}}_{\text{i}}}{\partial \text{t}}={\overline{\text{D}}}_{\text{i}}\frac{{\partial }^2{\stackrel{⌢}{\text{C}}}_{\text{i}}}{\partial {\text{X}}^2}+{\stackrel{⌢}{\text{R}}}_{\text{i}}$$ (1)

where, C̑_i is the volume averaged concentration of species i, ${\stackrel{\rightharpoonup }{\text{D}}}_{\text{i}}=\frac{2}{(3-{\epsilon }_{\text{mito}})}{\text{D}}_{\text{i}}$ (Whitaker, 1999) is the effective diffusion coefficient of species i, Ȓ_i are the volume averaged reaction rates, X is the non-dimensional distance, and t is time. This model included the reaction rate functions for the ATPases, mitochondrial ATP production, creatine kinase reaction, and myoglobin - O₂ binding. We used an aggregate ATPase function that yields reasonable rates of total ATP consumption during steady state contraction, and employed a Michaelis-Menten expression to model the ATP consumption rate

$${\stackrel{⌢}{\text{R}}}_{\text{ATPase}}=-\frac{{\text{V}}_{\text{max},\text{ATPase}}.{\stackrel{⌢}{\text{C}}}_{\text{ATP}}}{\left({\text{K}}_{\text{m},\text{ATPase}}+{\stackrel{⌢}{\text{C}}}_{\text{ATP}}\right)}$$ (2)

where, Ȓ_ATPase is the ATP consumption rate, V_max,ATPase and K_m,ATPase are the Michaelis-Menten kinetic constants, and C̑_ATP is the volume averaged ATP concentration. The volume averaging technique accounts for both the ATP production at the mitochondria and the ATP consumption in the intercellular space with a single differential equation. The mitochondrial reactions are scaled by the volume fraction of mitochondria and the volume fraction also determines the effective diffusion coefficient. In the volume averaging method it is assumed that concentration gradients between mitochondria are much smaller than those overall in the cell (Dasika et al., 2011). In addition, maximal steady-state rates of ATP production in aerobic fibers power ATPases associated with contraction, whereas in highly anaerobic fibers maximal rates of aerobic flux are associated with different ATP consuming processes during post-contractile recovery. Therefore, we used a consistent kinetic expression for ATP consumption and evaluated muscle function in a diversity of fibers within the physiological range of aerobic flux. We utilized the expression proposed by Morrison and James (1965) to model the CK reaction rate in the direction of ATP production

$${\stackrel{⌢}{\text{R}}}_{\text{CK}}=\frac{{\text{V}}_{\text{rev}}^{\text{CK}}{\stackrel{⌢}{\text{C}}}_{\text{ADP}}{\stackrel{⌢}{\text{C}}}_{\text{PCr}}-\left\{\frac{{\text{V}}_{\text{for}}^{\text{CK}}{\stackrel{⌢}{\text{C}}}_{\text{ATP}}{\stackrel{⌢}{\text{C}}}_{\text{Cr}}{\text{k}}_{\text{iADP}}{\text{k}}_{\text{PCr}}}{{\text{k}}_{\text{iATP}}{\text{k}}_{\text{Cr}}}\right\}}{{\text{k}}_{\text{iADP}}{\text{k}}_{\text{PCr}}+{\text{k}}_{\text{PCr}}{\stackrel{⌢}{\text{C}}}_{\text{ADP}}+{\text{k}}_{\text{iADP}}{\stackrel{⌢}{\text{C}}}_{\text{PCr}}+{\stackrel{⌢}{\text{C}}}_{\text{ADP}}{\stackrel{⌢}{\text{C}}}_{\text{PCr}}+\text{den}1}$$ (3)

where

$$\text{den}1={\text{k}}_{\text{iADP}}{\text{k}}_{\text{PCr}}\left\{\frac{{\stackrel{⌢}{\text{C}}}_{\text{ADP}}{\stackrel{⌢}{\text{C}}}_{\text{Cr}}}{{\text{k}}_{\text{iADP}}{\text{k}}_{\text{ICr}}}+\frac{{\stackrel{⌢}{\text{C}}}_{\text{Cr}}}{{\text{k}}_{\text{iCr}}}+\frac{{\stackrel{⌢}{\text{C}}}_{\text{ATP}}}{{\text{k}}_{\text{iATP}}}+\frac{{\stackrel{⌢}{\text{C}}}_{\text{ATP}}{\stackrel{⌢}{\text{C}}}_{\text{Cr}}}{{\text{k}}_{\text{iATP}}{\text{k}}_{\text{Cr}}}+\frac{{\stackrel{⌢}{\text{C}}}_{\text{ATP}}{\stackrel{⌢}{\text{C}}}_{\text{PCr}}}{{\text{k}}_{\text{iATP}}{\text{k}}_{\text{IPCr}}}\right\}$$ (4)

where Ȓ_CK is the CK reaction rate in the direction of ATP formation. The Mb-O₂ binding reaction rate is modeled using a simple kinetic expression as

$${\stackrel{⌢}{\text{R}}}_{\text{Mb}}=-{\text{k}}_{1,\text{Mb}}\stackrel{⌢}{\text{C}}{}_{\text{Mb}{\text{O}}_2}+{\text{k}}_{2,\text{Mb}}{\stackrel{⌢}{\text{C}}}_{\text{Mb}}{\stackrel{⌢}{\text{C}}}_{{\text{O}}_2}$$ (5)

O₂ is assumed to be delivered into the cell via capillaries at the cell periphery and across the cell membrane. The steady state volume averaged concentrations and rates were then computed. The effectiveness factor (η) (Weisz, 1973) was computed from the ratio of the ATPase rate for the case with intracellular diffusion constraints to that without diffusion limitations. In the following text, enhancing diffusion refers to offsetting diffusion constraints.

In order to determine the effects of CK alone, the Mb O₂ binding reaction was set to zero and the metabolites ATP, ADP, P_i, O₂, Cr, and PCr were considered. Similarly, in order to analyze the effects of Mb alone, the CK reaction was set to zero and the metabolites ATP, ADP, P_i, O₂, Mb, and MbO₂ were included. In the last case, both the CK and Mb rates were set to zero and only the metabolites ATP, ADP, O₂, and P_i were utilized in order to determine the effects of absence of both of these reactions. The steady-state concentrations of all metabolites and the spatially averaged (represented by ‘<>’) concentrations and ATPase rates were computed for all the cases. For the cases without diffusion limitations computations were made as described in (Locke and Kinsey, 2008, Dasika et al., 2011). To quantify the facilitated diffusion roles of Mb and CK we computed the ratio of η with Mb alone, with CK alone, and with Mb and CK to the case without Mb and CK. In all of the calculations we employed K_m,ATPase = 0.15 mM. To determine the general effects of the Mb and CK reactions, the diffusion length, L, which is the fiber radius, was varied from 25 to 150 μm and the maximal velocity of the ATPase (V_max,ATPase) was varied from 1 – 15 mM/min. In all calculations where Mb is present the total Mb complex concentration was 100 times the boundary O₂ concentration (O₂⁰). For comparison to experimental data, L and V_max,ATPase were varied for specific values of mitochondrial volume density (ε_mito), and η was computed for the cases with and without Mb and CK. Here, the L was varied from 5 – 50 μm and V_max,ATPase was varied from 1 – 120 mM/min for ε_mito = 0.1 and 0.25, while L was varied from 1 – 25 μm and V_max,ATPase was varied from 1 – 3600 mM/min for ε_mito = 0.45. The experimental data was then overlaid on the η surface as a function of the spatially averaged ATPase reaction flux (<R_ATPase>) and L. Also, animals with mitochondrial volume density in the ranges of 0.006 - 0.016, 0.024 – 0.062, 0.07 – 0.17, 0.22 – 0.29, and 0.32 – 0.43 were plotted together on the η surface with ε_mito = 0.01, 0.05, 0.1, 0.25, and 0.45, respectively.

To analyze the effects of Mb and CK on η with varying mitochondrial volume fraction and boundary O₂ concentration, we used ε_mtio = 0.01, 0.1, and 0.45 and two different boundary O₂ concentrations, O₂⁰ = 35.1 μM (PO₂ = 20 Torr) representing normoxic capillary PO₂ in working muscle (Roy and Popel, 1996; van der Laarse et al., 2005) and O₂⁰ = 7.85 μM (PO₂ = 4.5 Torr) representing hypoxic conditions.

To evaluate the possible functions of Mb and CK as temporal buffers, we computed the transient concentrations as they approached steady state. We solved the four cases, i.e., without Mb and CK, with Mb alone, with CK alone, and with Mb and CK, for 100 s and computed the averaged concentrations. In these calculations, we employed the following conditions: V_max,ATPase = 120 mM/min, K_m,ATPase = 0.15 mM, L = 15, μm, ε_mito = 0.25, and O₂⁰ = 35.1 μM. To evaluate the transient effect of Mb alone when blood O₂ was low, we solved the cases with Mb alone and without Mb and CK, and computed the <O₂> with the following conditions: V_max,ATPase = 120 mM/min, K_m,ATPase = 0.15 mM, L = 15, μm, ε_mito = 0.25, and O₂⁰ = 7.85 μM.

Results

Fig. 1 shows that <ATP> is maintained at higher levels for larger V_maxATPase and greater length scales in the presence of CK (Figs. 1C and 1D) than without (Figs. 1A and 1B). This is consistent with spatial buffering of ATP by the CK reaction. In contrast, Mb has no observable effect on <ATP> (Fig. 1B). <O₂> was slightly higher in the presence of Mb (Fig. 2B and 2D), whereas no significant effect of CK was observed on oxygen concentration (Fig. 2C). However, a small effect of Mb on <O₂> was observed only for very large fibers with very low ATP demand, characteristics of highly anaerobic fibers such as fish white muscle, that do not express Mb. In small fibers with a relatively high ATP demand, there was no effect of Mb on <O₂>.

Fig. 1.

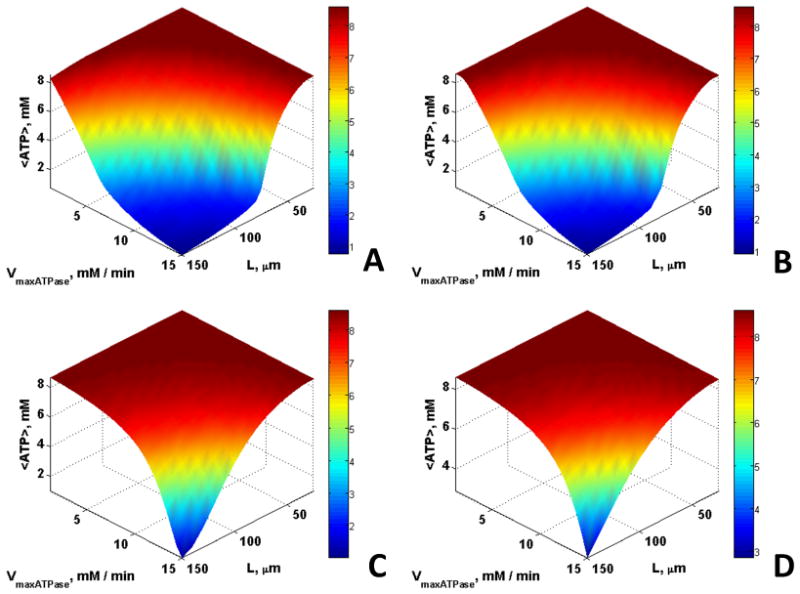
The influence of Mb and CK on the spatially averaged ATP concentration, <ATP>, for ε_mito = 0.1 and O₂⁰ = 35.1 μM for cases (A) Without Mb and CK, (B) With Mb, (C) With CK, (D) With Mb and CK; <ATP> is buffered at higher rates of ATP demand and over longer diffusion distances in the presence of CK whereas Mb has no effect.

Fig. 2.

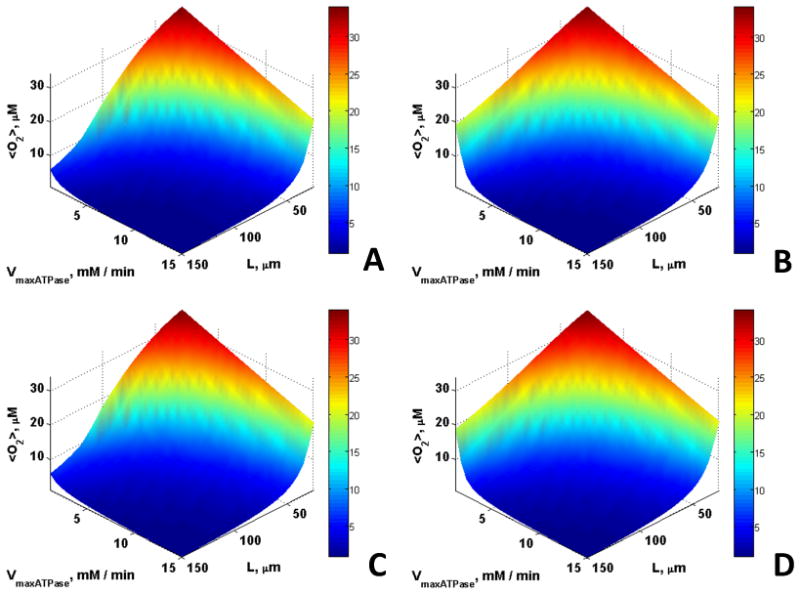
The influence of Mb and CK on the spatially averaged free or unbound O₂ concentration, <O₂> for ε_mito = 0.1 and O₂⁰ = 35.1 μM for cases (A) Without Mb and CK, (B) With Mb, (C) With CK, (D) With Mb and CK; <O₂> is slightly higher in the presence of Mb for low V_max,ATPase and large length scales whereas CK has no effect.

Experimental data comparison

Comparison of the model results with a wide range of experimental data obtained from the literature and the effects of removing the CK and Mb reactions are shown in Figs. 3 and 4. The experimental data plotted on the surfaces in Figs. 3 and 4 represents muscle from mammals (including humans), fishes, amphibians, reptiles and crustaceans, and there is wide variation in fiber size mitochondrial densities, and aerobic metabolic rates. These data were taken from the literature as described previously (Locke and Kinsey (2008), Jimenez et al., (2008), Dasika et al., (2011), Kinsey et al., (2007). In the aerobic fibers plotted here (smaller fibers with higher R_ATPase and ε_mito), the maximal rates of aerobic metabolism power steady state muscle contraction, whereas in the anaerobic fibers (larger fibers with lower R_ATPase and ε_mito), the maximal rates of aerobic metabolism power non-contractile processes like post-contractile recovery. Clearly these results support our previous study where we found that most muscle fibers are not limited by diffusion under typical physiological conditions, while some fibers, including those of mammals, operate at the edge of substantial diffusion limitations (Dasika et al., 2011). Figs. 3 and 4 show experimental results over a wider range of mitochondrial volume fractions and cell size than in our previous work. No detectable effects of Mb and CK on the effectiveness factors were observed for all five mitochondrial volume fractions studied. Since Mb and CK have long been proposed to facilitate the diffusion of metabolites and O₂, we expected enhancement in diffusion at the upper limits of L or V_max,ATPase. It was surprising to observe no effects of the presence of Mb and CK even at these upper limits except for the case of low mitochondrial volume fraction of 0.01 (Figs. 3A and 3B).

Figure 3.

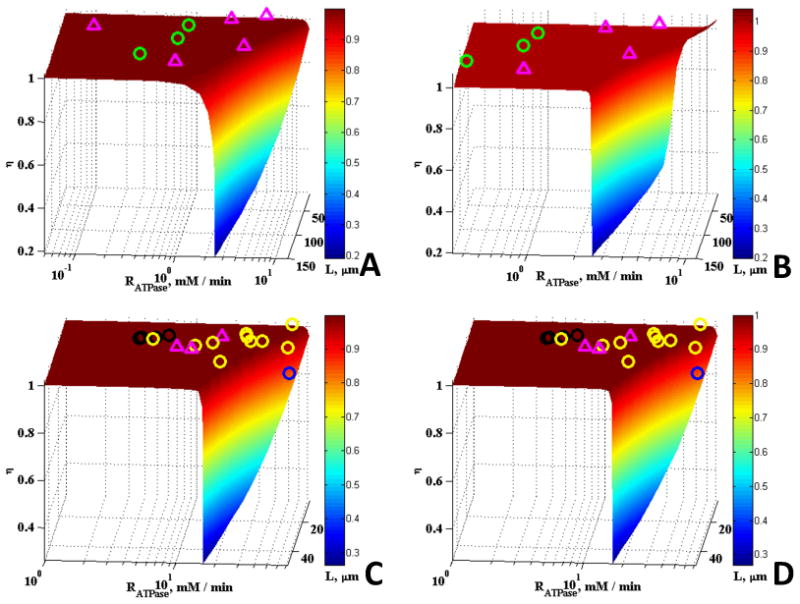
Effect of <R_ATPase> and L on η with experimental data plotted for a variety of fibers: (A) ε_mito = 0.01, case without Mb and CK, (B) ε_mito = 0.01, case with Mb and CK, (C) ε_mito = 0.025, case without Mb and CK, (D) ε_mito = 0.025, case with Mb and CK. In these plots, purple triangles, green, black, yellow, and blue circles represent data for fishes, crustaceans, reptile, mammal, and amphibian species respectively.

Figure 4.

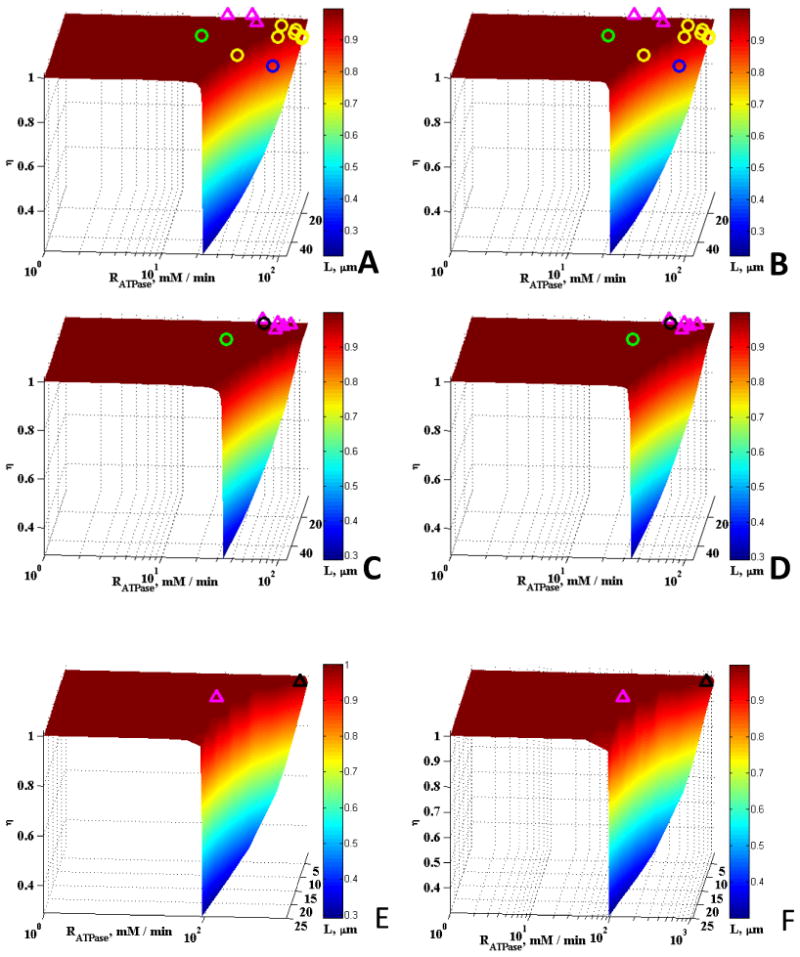
Effect of <R_ATPase> and L on η with experimental data plotted for a variety of fibers: (A) ε_mito = 0.1, case without Mb and CK, (B) ε_mito = 0.1, case with Mb and CK, (C) ε_mito = 0.25, case without Mb and CK, (D) ε_mito = 0.25, case with Mb and CK, (E) ε_mito = 0.45, case without Mb and CK, (F) ε_mito = 0.45, case with Mb and CK. In these plots, purple triangles, green, black, yellow, and blue circles represent data for fishes, crustaceans, reptile, mammal, and amphibian species respectively.

In these plots (Fig. 3 & 4), animals with mitochondrial density ranging from 0.006 - 0.016, 0.024 – 0.062, 0.07 – 0.17, 0.22 – 0.29, and 0.32 – 0.43 were plotted on the η surface for ε_mito = 0.01, 0.025, 0.1, 0.25, and 0.45, respectively. Data and calculations are from Locke and Kinsey (2008), Jimenez et al., (2008), Dasika et al., (2011), Hardy et al., (2009, 2010), Kinsey et al., (2007). The crustacean muscles that are plotted on panels A-D contain arginine kinase instead of creatine kinase, but the reactions are functionally and kinetically similar.

Effectiveness factor ratio comparisons

To quantify the effects of Mb and CK on enhancing diffusion, the ratios of η for the cases with Mb alone, CK alone, and with Mb and CK to the case without Mb and CK are shown in Fig. 5 for the intermediate volume faction and cell sizes (ε_mito = 0.25, L = 5 – 50 μm) with conditions identical to those in Figs. 4C and 4D. These plots (Fig. 5) show the extent to which the diffusion limitation of aerobic flux is overcome due to the presence of Mb and CK as functions of L and R_ATPase. The maximum ratio of η for the case with Mb alone to that without Mb and CK is only 1.0045 (0.45 % increase in η) while the ratio of η for CK alone to that without Mb and CK shows an 8 % increase in η, implying that CK has a larger effect on enhancement of metabolite diffusion compared to Mb. However, the magnitudes of the effects of Mb and CK were not large, even at high ATP demand, for this case with intermediate volume fraction and length. In addition, as reaction-diffusion theory would suggest these effects are observed only in the narrow transition region where diffusion limitations become important and not in the broad region where chemical reaction controls.

Figure 5.

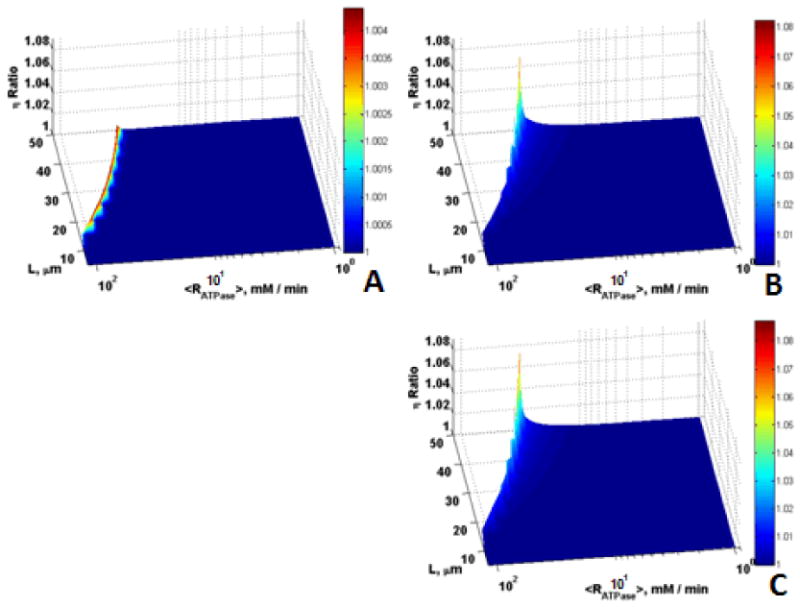
Role of Mb and CK in offsetting diffusion constraints for O₂⁰ = 35.1 μM, ε_mito = 0.25, L = 5 – 50 μm, and V_max,ATPase = 1 – 120 mM/min; Surfaces are the ratio of (A) η with Mb vs. without Mb and CK, (B) η with CK vs. without Mb and CK, (C) η with Mb and CK vs. without Mb and CK, vs. L and <R_max,ATPase> for higher mitochondrial volume fraction, smaller size cells and larger ATPase rates.

For larger cells (L = 25 - 150 μm) and lower mitochondrial volume fraction (ε_mito = 0.1) the maximum ratio of η for the case with Mb alone to that without Mb and CK is 1.18 (18% increase in η, Fig. 6A) while the maximum ratio of η for CK alone to that without Mb and CK is 2 (100% increase in η, Fig. 6B), implying that CK has a larger effect on enhancement of metabolite diffusion compared to Mb. Although cells this large may not contain Mb, the results for this hypothetical case show the range of parameters where Mb and CK can have effects to enhance diffusion. The maximum ratio occurs at extremes in fiber size that are characteristic of white muscle from fish, which have low aerobic metabolic rates and no Mb. Comparison of Fig. 5 with 6 shows that the effects of Mb and CK on enhancing diffusion are large for larger cells with moderately high ATP demand compared to smaller cells with high ATP demand.

Figure 6.

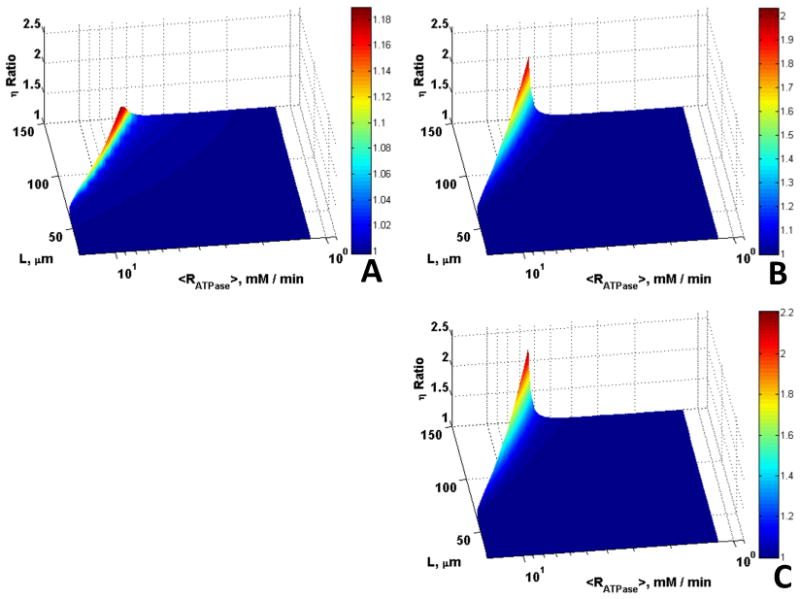
Role of Mb and CK in offsetting diffusion constraints over a broad range of diffusion distances and rates of aerobic ATP demand for O₂⁰ = 35.1 μM, ε_mito = 0.1, L = 25 – 150 μm, and V_max,ATPase = 1 – 15 mM/min. Surfaces are the ratio of (A) η with Mb vs. without Mb and CK, (B) η with CK vs. without Mb and CK, (C) η with Mb and CK vs. without Mb and CK, vs. L and <R_max,ATPase>; significantly higher η ratio can be observed in the presence of CK, and the extreme (large L of 150 μm and V_max,ATPase of 15 mM/min), where the cell operates under diffusion limitation.

Effect of Mitochondrial Volume Fraction, ε_mito

Higher ε_mito results in larger amounts of ATP produced by mitochondria and shorter diffusion distances for ATP/ADP between sites of ATP production and ATP consumption. Thus, the effects of CK are expected to be lower as the ε_mtio increases. Fig. 7 shows plots of the ratio of η in the presence of Mb and CK to that when these species are absent for a range of mitochondrial volume fractions. Mb and CK together have substantial effects for low volume fraction (ε_mito = 0.01, Fig. 7A), where the maximum ratio is 4.5, while the maximum η ratio decreases with increases in ε_mtio (maximum ratio is 2.2 for ε_mtio = 0.1, Fig. 7B and 1.7 for ε_mtio = 0.45, Fig. 7C). Again, however, the combined effects of Mb and CK are most predominant at the transition between reaction and diffusion control for the larger cells.

Figure 7.

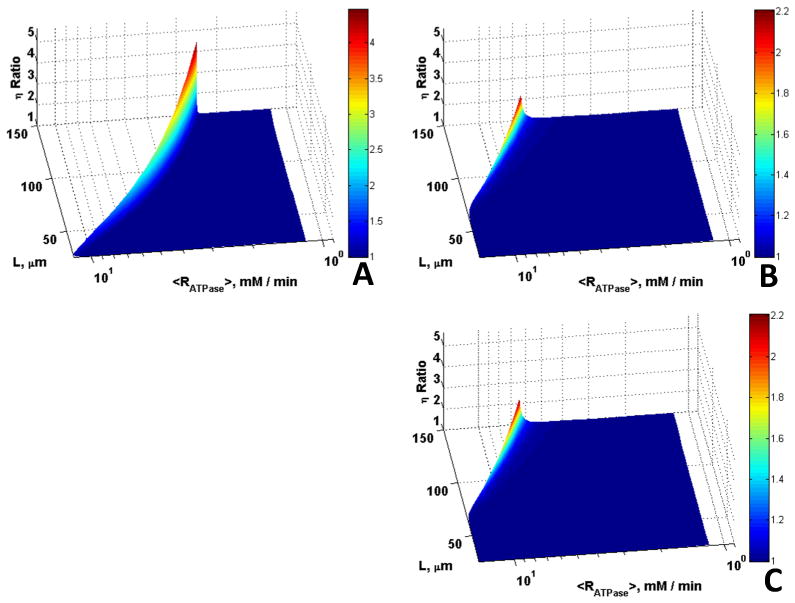
Role of Mb and CK in offsetting diffusion constraints as a function of mitochondrial volume density. Surfaces are the ratio of η vs. L and for <R_ATPase> for the case with Mb and CK to the case without Mb and CK for (A) ε_mito = 0.01, (B) ε_mito = 0.1, (C) ε_mito = 0.45; the effects of Mb and CK decrease with increase in ε_mito.

Effect of Boundary Oxygen Supply, O₂⁰

As the boundary O₂ concentration decreases the amount of O₂ available for ATP production by aerobic metabolism decreases, while the diffusion distance for ATP/ADP increases with decreases in ε_mtio. Therefore, the effects of Mb and CK would be expected to increase with decreases in ε_mtio and boundary O₂ concentration. Fig. 8 clearly indicates this trend whereby at low oxygen and low volume fraction (O₂⁰ = 7.85 μM and ε_mtio = 0.1) the effectiveness factor ratios are larger than for the cases with higher oxygen and volume fraction shown in Fig. 6. It is important to emphasize that even in these cases the effects of Mb and CK only occur in the transition between reaction and diffusion control. Since η is a function of <R_ATPase>, which in turn is dependent on the <ATP>, higher η would imply higher <ATP> and <R_ATPase>. Under hypoxic conditions the skeletal muscle fibers may sustain higher ATP demand in the presence of Mb and CK without being diffusion limited (Fig. 8).

Figure 8.

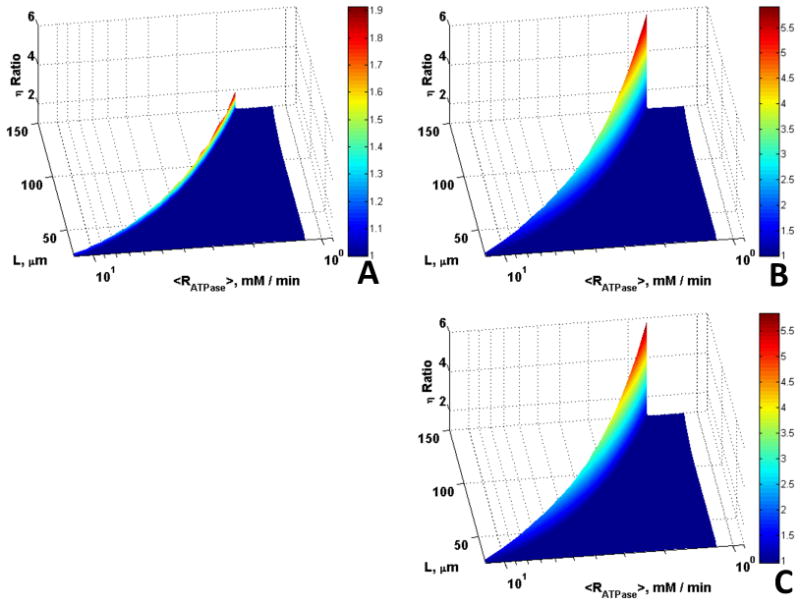
Role of Mb and CK in offsetting diffusion constraints under hypoxic conditions (compare to the normoxic case in Fig. 5). Surfaces are the ratio of (A) η with Mb vs. without Mb and CK, (B) η with CK vs. without Mb and CK, (C) η with Mb and CK vs. without Mb and CK, vs. L and <R_max,ATPase> for O₂⁰ = 7.85 μM; the η ratio is larger for lower O₂⁰, the enhancement in diffusion due to Mb increases as O₂⁰ decreases.

Transient Effects

Figs. 9A and 9B show the transient <ATP> and <O₂> for all four cases. CK had a large temporal buffering effect on <ATP> and <O₂>, while the influence of Mb on <ATP> was detectable but comparatively small (Fig. 9A and 9B). Under low O₂ conditions, the temporal effects of Mb on <O₂> are apparent, but again of relatively low magnitude (data not shown). Thus, in our analysis CK has a large temporal <ATP> buffering role, while Mb is a modest temporal buffer of <ATP> and <O₂>. To analyze the temporal buffer effects of Mb and CK in the transition from reaction to diffusion control, we computed the transient <ATP> for various ATP demands. Fig. 10 shows the plots of <ATP> with and without Mb and CK with varying ATP demand. Clearly when the cell is not limited by diffusion (V_max,ATPase < 120 mM/min), Mb and CK function as temporal buffers. The cell begins to be limited by diffusion for V_max,ATPase larger than 120 mM/min. This is evident from Fig. 10 A – C. Although the temporal buffering effects of Mb and CK appear larger at low V_max,ATPase, relatively small amounts of ATP are consumed even for the case without Mb and CK; hence the temporal buffer effect of Mb and CK is smaller for low V_max,ATPase. The cell will be limited by diffusion for V_max,ATPase = 150 mM/min. Therefore, Mb and CK start to function as facilitators of diffusion for high V_max,ATPase where the temporal buffering effects decreases (Fig. 10D).

Figure 9.

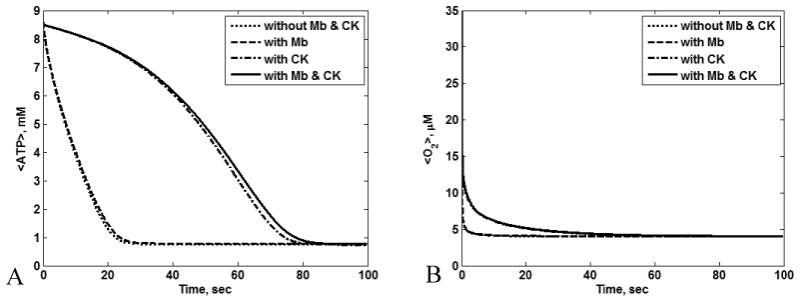
Transient (A) <ATP> and (B) <O₂> for cases with and without Mb and CK for O₂⁰ = 35.1 μM, ε_mito = 0.25, V_max,ATPase = 120 mM/min, and L = 15 μm; CK functions as temporal buffer while the temporal buffering effect of Mb is very small. Under these conditions, the <R_ATPase> for the case without Mb and CK, with Mb alone, with CK alone, and with Mb and CK are 97.71, 97.73, 97.73, and 97.75 mM/min, respectively. In these plots, the <ATP> with Mb alone overlaps with the <ATP> without Mb and CK alone and the <ATP> with CK alone overlaps with <ATP> with Mb and CK (Fig. 9A) while the <O₂> with Mb alone over laps with the <O₂> without Mb and CK and <O₂> with CK alone overlaps with <O₂> with Mb and CK (Fig. 9B).

Figure 10.

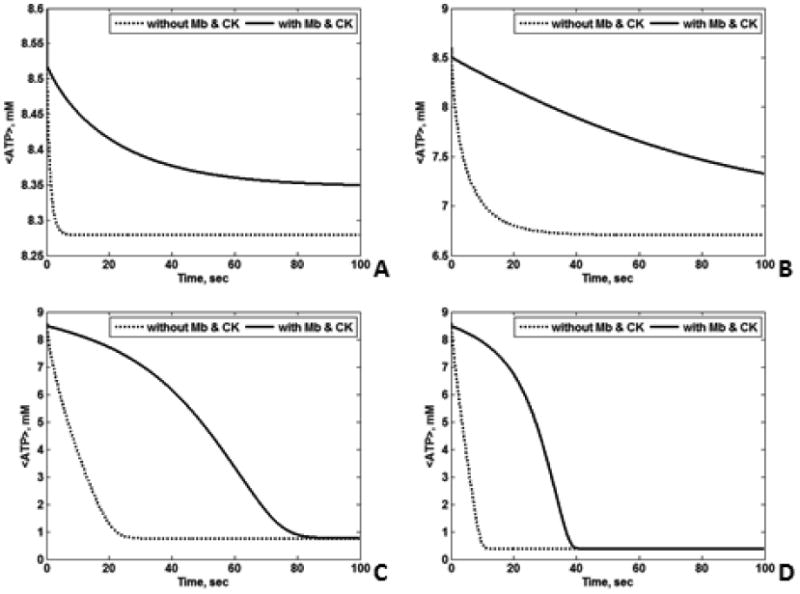
Transient <ATP> with Mb and CK (solid black line) and without Mb and CK (dotted black line) for L = 15 μm, ε_mito = 0.25, O₂⁰ =35.1 μM, and (A) V_max,ATPase = 60 mM/min, (B) V_max,ATPase = 90 mM/min, (C) V_max,ATPase = 120 mM/min, (D) V_max,ATPase = 150 mM/min. As the V_max,ATPase increases, the cell starts to be limited by diffusion. When the cell is not limited by diffusion, Mb and CK play the role of temporal buffers. Note the different scaling of the <ATP> axis.

Discussion

Our mathematical analysis and comparison to experimental data found that under steady-state conditions (I) CK is important in buffering ATP concentration, and therefore dramatically extending the range of fiber size and reaction rate over which fibers can maintain aerobic ATP turnover (Fig. 1), (II) Mb has essentially no similar effect on free O₂ concentration (Fig. 2), (III) aerobic metabolism in skeletal muscle is generally not diffusion controlled over a broad range of fiber size and metabolic rate (Fig. 3 & 4), (IV) CK and Mb play almost no role in facilitated diffusion under steady-state conditions, particularly in the aerobic fibers in which this function is thought to be important (Figs. 3-8) and (V) CK has a large transient effect as an ATP buffer, whereas the effect of Mb is small (Figs. 9 - 10). Our result of minimal facilitated diffusion effect of Mb is consistent with other theoretical studies on skeletal muscle fibers. For example Federspiel (1986) employed a 2-D circular cell model and solved for steady state Mb, O₂, and Mb-bound-O₂ concentrations and observed minimal facilitated diffusion effect of Mb under normoxic conditions. However, the author did not include the effects of the phosphagen kinase system or detailed analysis of the mitochondrial function (Federspiel 1986).

Facilitated diffusion theory has long been invoked to explain in part the functional roles of CK (Meyer et al., 1984) and Mb (Wittenberg, 1959) in skeletal muscle. There is no disagreement that CK and Mb facilitate diffusion to some extent, as it is an inevitable consequence of the near equilibrium nature of the CK reaction and rapid binding of Mb to O₂, coupled with free diffusion of Cr/PCr and Mb/Mb-O₂. Rather, the relative importance of this role has been debated. The model evaluated here is not intended to capture all details of CK and Mb in highly aerobic cells. For instance, we have not accounted for the inhomogeneous distribution of mitochondria, which has been shown experimentally to respond to diffusion constraints (Hardy et al., 2009, 2010; Kinsey et al., 2007, 2011; Boyle et al., 2003; Nyack et al., 2007; Pathi et al., 2011). However, since an inhomogeneous mitochondrial distribution helps alleviate diffusion constraints, this simply makes our model more prone to a facilitated diffusion effect. In the CK system, we have not evaluated potential metabolic compartmentation that may restrict diffusion, enzyme localization or substrate channeling (reviewed in Bessman and Geiger, 1981; Wallimann et al., 1992; Wyss and Kaddurah-Daouk, 2000; Dzeja and Terzic, 2003; Ingwall, 2004). Again, however, these features of some mammalian cells are thought to reduce distances and otherwise overcome diffusion constraints, adding support to our conclusions about the facilitated diffusion function of CK. Similarly, we have not included in our examination of Mb some of the other roles that it plays, including as a scavenger of reactive oxygen species and nitric oxide (Wittenberg and Wittenberg, 2003; Ordway and Garry, 2004; Brunori, 2001; Flögel et al., 2001). However, the present reaction-diffusion analysis allows investigation of a wide range of diffusion distances and reaction rates that captures much of the diversity of muscle fibers found in the animal kingdom, all of which have high phosphagen kinase activity and some of which contain Mb. Thus, if a principal function of CK and Mb in aerobic mammalian fibers is to facilitate diffusion, then this role might be expected to apply broadly to skeletal muscle.

Since these cells function in reaction control, the only way that facilitated diffusion could be important would be if in the absence of the facilitator, the cells operate in a diffusion controlled regime. The results of our work suggest that even in the absence of a putative facilitator (CK and Mb) skeletal muscle fibers that vary greatly in diffusion distance and aerobic ATP demand are reaction controlled (Fig. 3 & 4) as indicated by effectiveness factors near unity. Nevertheless, analysis of extremes in cell size (Fig. 6), mitochondrial volume fraction (Fig. 7), and oxygen supply (Fig. 8) indicate that facilitated diffusion can be of modest importance in muscle that might function within the transition regions between reaction and diffusion control. The fact that some cells function near this transition region suggests that in some cases, particularly at low oxygen supply, the facilitated diffusion roles of CK and Mb may be important in preventing diffusion control. However, our results show that CK and Mb facilitated diffusion are most important in very large fibers with low mitochondrial content (and therefore low rates of aerobic ATP turnover), such as fish white muscle. Ironically, these are fiber types where CK is generally thought to function primarily as a temporal ATP buffer during burst contractions, and Mb is not even present. As fiber size decreases and metabolic rate increases, facilitated diffusion by CK and Mb becomes less important (Figs. 5 - 8). That Mb is not even expressed in muscle fiber types where its facilitated diffusion function would be most important (large diffusion distances and low metabolic rates), but rather it is found in cells with a high and variable O₂ supply, is indirect evidence that steady-state facilitated diffusion is not a primary function.

Hypoxia leads to a contraction of the diffusion distance/metabolic rate domain over which a high η is maintained (Dasika et al., 2011) and some of the fibers that are near diffusion limitation in Fig. 3 would have a reduced η at a lower PO₂. This is apparent by comparing the size of the plotted surfaces in Fig. 6 (normoxia) with Fig. 8 (hypoxia). However, analysis of Fig. 8 reveals that even under hypoxia, where some fibers might be expected to become diffusion limited, the influences of CK and Mb are limited to the narrow transition region between reaction and diffusion control, and it is only important in very large anaerobic fibers. Fibers with a radius of 25 μm, which is the approximate upper size range for aerobic fibers, are barely influenced by CK and Mb facilitated diffusion at steady state under hypoxia, and the influence of Mb is far less than that of CK (Fig. 8). The influence of CK and Mb facilitated diffusion is even less important in smaller fibers (Figs. 3 - 5).

The results of the present study are consistent with the original steady-state facilitated diffusion analysis of CK by Meyer et al. (1984) in mammalian muscle, who found that the bulk of ATP equivalents were carried in the form of PCr, rather than as ATP. However, this effect was shown to be predominantly due to the higher concentration of PCr than ATP, and concentration gradients of high energy phosphates were minimal (Meyer et al., 1984). Our results show that this is the case for a wide range of fibers, and the near lack of concentration gradients means that facilitated diffusion is generally unimportant. Similarly, our results for Mb are consistent with the fact that the relatively low diffusion coefficient of Mb in muscle fibers limits its capacity to facilitate O₂ diffusion, although, again, the facilitated diffusion role may become important at very low PO₂ (Jürgens et al., 1994; Papadopoulos et al., 1995; Lin et al., 2007a, 2007b) in fibers that are near the boundary of reaction and diffusion control.

In a recent review Gros et al. (2010) noted that the temporal buffering role of Mb is apparent in skeletal muscle by the desaturation that occurs during rest-to-work transitions, which indicates a transient mismatch between O₂ supply and demand. Thus, Mb facilitated diffusion of O₂ may be important under non-steady state conditions when the P_O2 is less than the equipoise P_O2 of approximately 4 Torr in skeletal muscle fibers, which may occur during intense exercise or rapid changes in O₂ demand.

In our transient analysis <ATP> was clearly higher in the presence of CK, while the effects of Mb on <ATP> were small compared to that of CK (although not negligible) (Fig. 9). The temporal buffering effects of Mb and CK decrease as the ATP demand increases, i.e., as the fiber starts to be limited by diffusion and where Mb and CK function as facilitators of diffusion (Fig. 10). This transient analysis suggests that in fibers where the soluble form of CK predominates, as simulated here, the primary function of CK is to temporally buffer rather than to facilitate diffusion. Nevertheless, the observation of a large temporal effect of CK and a modest effect of Mb suggests a functional significance under transient conditions that is much stronger than steady state facilitated diffusion. The clear importance of CK during changes in ATP demand is consistent with the physiological responses to CK knockout in mice (van Deursen et al., 1993). Similarly, Gros et al. (2010) have argued that the relatively subtle temporal effects of Mb can account for the observed physiological compensations to Mb knockout (Garry et al., 1998; Gödecke et al., 1999).

The mathematical model utilized in the present work incorporates all of the relevant species balances and chemical reactions within the cellular domain, and, as such, it is a more general formulation than classical facilitated diffusion theory, where a solute crosses a defined domain with fixed concentrations at the boundaries. We have shown in previous studies (Locke and Kinsey, 2008) for the case of only ATP transport and reaction (in the inter-mitochondrial space and neglecting oxygen), that the exact solution of the full reaction-diffusion model reduces to the approximations of classical facilitated diffusion theory, but that the solution to the complete reaction-diffusion model provides a broader range of results in regions where the assumptions of the classical facilitated diffusion theory do not apply, e.g., in reaction control. Numerical solution of the more general reaction-diffusion model is thus not limited to the domain of applicability of facilitated diffusion and it therefore provides a means to assess the transition between reaction control (where facilitated diffusion can have no role) and diffusion control (where facilitated diffusion plays a major role).

Conclusions

Experimental data comparison with the model shows that over a broad range of size, muscle fibers are not limited by diffusion under steady state conditions, although some fibers appear to operate at the edge of diffusion limitation. Mb and CK play insignificant roles in enhancing diffusion during steady-state ATP turnover in the biologically relevant range. The facilitated diffusion effects of Mb and CK are greatest for large cells that have relatively low ATP demand, which, ironically, are fiber types where CK is thought to serve almost exclusively as a temporal buffer and that do not express Mb. As the mitochondrial volume fraction and boundary O₂ decrease, the effects of Mb and CK on enhancing metabolite diffusion increase, although the effects are still small. Thus CK and, to a lesser extent, Mb may primarily function as temporal buffers rather than facilitating diffusion under steady-state conditions in the biologically relevant range.