Approximations for the hitchhiking effect caused by the evolution of antimalarial-drug resistance

Abstract

An analytically feasible, deterministic model for the spread of drug resistance among human malaria parasites, which incorporates all characteristics of the complex malaria-transmission cycle was introduced by Schneider and Kim (Theor. Popul Biol, 2010). The model accounts for the fact that only a fraction of infected hosts receive drug treatment and that hosts can be co-infected by differently many parasites. Furthermore, the model also incorporates host heterogeneity. Antimalarial-drug resistance is assumed to be caused by a single locus with two alleles—a sensitive one and a resistance one. The most important result for this model is that an analytical solution for the frequencies of a linked neutral biallelic locus exists. However, the exact solution does not admit an explicit form, and cannot straightforwardly be interpreted in terms of the model parameters. Here, we establish simple approximations for the equilibrium frequency at the neutral locus. Under the assumption that the resistant allele is initially rare—the biologically most relevant assumption in this context—and that recombination is weak, the approximations become similar to the approximations in the standard hitchhiking model. However, there are crucial differences. In particular, because of the high degree of selfing among malaria parasites in their sexual phase, a genome-wide reduction of relative heterozygosity occurs if selection is sufficiently strong. It turns out that the approximations are accurate even if the recombination rates are not small and the resistant allele is initially not very rare. The main advantage of our approximations is that they are easy to interpret in terms of model parameters. Moreover, they allow to make predictions of the size of the valley of reduced heterozygosity around the selected locus for given model parameters. Reversely, for a given reduction of heterozygosity, it is possible to identify the corresponding parameters. Moreover, we will show that incorporating host heterogeneity leads to an increased hitchhiking effect.

1 Introduction

Human malaria is an infectious disease caused by parasites belonging to the genus Plasmodium, which is endemic in most tropical and subtropical regions in the world. Infections with Plasmodium falciparium, the most virulent form of human malaria, result worldwide in one to 3 million deaths per year (cf. WHO 2000; Korenromp et al. 2005). Malaria control is highly dependent on drug treatments that kill parasites in infected hosts. However, attempts to control malaria have been thwarted by rapid evolution of antimalarial-drug resistance, a fact that has been described to be a public health disaster (cf. Marsh 1998).

The limited repertoire of safe, effective, and affordable antimalarial drugs has made research on the emergence and dispersion of resistance a global health priority. Mathematical models that can use input from genetic data to investigate the dynamics of mutations associated with drug resistance are urgently needed for designing drug-deployment policies that can increase the lifespan of the available drugs. This requires a detailed understanding of population genetic processes that lead to the emergence and dispersion of drug resistance. Unfortunately, the highly complex nature of the malaria-transmission cycle as well as complex demographic and environmental factors aggravate the efforts to elaborate theoretical models.

Malaria parasites undergo a complex transmission cycle with sexual phases in the mosquito vector and asexual phases in the infected host (cf. e.g. Daily 2006; Prugnolle et al. 2009). A human host is inoculated with sporozoites by the bite of an infected Anopheles mosquito during its blood meal. In the human host the sporozoites migrate first to the liver where they differentiate into hepatic merozoites. These are released into the blood stream where some of the hepatic merozoites form gametocytes. The haploid gametocytes are extracted by a mosquito during its blood meal and immediately reproduce sexually in the mosquito’s gut. Consequently, they undergo recombination. Completing the transmission cycle, this step is followed by the production of haploid sporozoites in the mosquitos’s salivary glands from which they can be inoculated into a human host.

Another source of complication is that many environmental and clinical factors differ significantly across the worldwide distribution of this parasite. The transmission rate and hence the number of secondary infections varies from very low rates in parts of South America, over intermediate rates in Southeast Asia, to high rates in Africa. On the other hand the level of host-acquired immunity is much higher (which means a high number of asymptomatic infections) in most of the affected areas in Africa than in other parts of the world. Such variation in host-acquired immunity affects drug use.

Among others, two important variables that summarize the demographic and clinical setting of the particular geographic area are the (average) number of parasites (m) co-infecting a given host (the average multiplicity of infection), which is determined by transmission intensity, and the proportion (α) of infected hosts that are drug treated. This parameter depends mainly on how many hosts acquired immunity.

Several studies built population genetic models that demonstrated profound effects of m and α on the rate of drug-resistance evolution (Hastings and Mackinnon 1998; Mackinnon and Hastings 1998; Hastings 2003,2006). However, it is still unclear which mechanisms are important to the spread of resistance, i.e., intra-host dynamics, drug half life, multiple drug treatment, migration, multiple infections, recombination, mutation etc.

Over the last 2 decades substantial advances regarding the genetic basis of antimalarial-drug resistance have been made. It is known that specific point mutations in the dhfr and dhps regions underlie resistance to pyrimethamine and sulfadoxine (cf. Cowman et al. 1988; Triglia and Cowman 1994; Brooks et al. 1994), that point mutations in mitrochandrial DNA underlie resistance to atovaquone (cf. Schwobel et al. 2003), and that mutations in the pfcrt gene are causing resistance against Chloroquine (CQ).

The spread of mutations causing drug resistance leads to a valley of reduced genetic variation at linked neutral regions. This removal of pre-existing variation occurs because recombination cannot effectively break the initial association with the neutral background in which the mutant first occurred, a process known as genetic hitchhiking or a selective sweep (Maynard Smith and Haigh 1974; Stephan et al. 1992; Barton 2000). For instance, Nair et al. (2003) observed a severe reduction of variation at microsatellite loci spanning over a 100 kb region surrounding the dhfr gene in a Southeast Asian population of P. falciparum. The extent of this pattern depends on how fast the favored allele increases to high frequency while meiotic recombination is constantly eroding the association between the favored allele and the surrounding chromosome segment (Kim and Stephan 2002). Selective sweeps have been initially studied for randomly mating populations of constant size, and homogenous constant selection pressures (e.g., Maynard Smith and Haigh 1974), to which we refer as the ‘standard model’, or standard ‘hitchhiking’.

In malaria biology, detection of selective sweeps mainly contributed to confirming the location of drug resistant mutations and elucidating their mutational origins (Wootton et al. 2002; Nash et al. 2005; Mita et al. 2007; Nair et al. 2007; McCollum et al. 2008), while fewer studies attempted to relate the span of selective sweeps with the strength of drug selection (Nair et al. 2003). Recently, Schneider and Kim (2010) introduced an analytical feasible model for the spread of antimalarial-drug resistance, which allows to study genetic hitchhiking. The model covers the important characteristics of the transmission cycle, incorporates host heterogeneity, i.e., different classes of treated and untreated hosts, and accounts for the fact that hosts can be infected by differently many parasites. Moreover, the model allows simple conditions for the spread of resistance and its speed in terms of the fitness parameters and α. Hence, it is useful to find ‘optimal’ treatment strategies to prevent or slow down the spread of resistance (for more discussion see Schneider and Kim 2010).

Studies based on known recombination rates and the result of the standard model of selective sweeps concluded that the observed patterns of selective sweeps are compatible with the predictions (Nair et al. 2003). However, Schneider and Kim (2010) discuss in detail why the application of the standard selective-sweep model to a malaria-parasite population is highly problematic. In particular, the high degree of selfing among malaria parasites will lead to a genome-wide reduction of heterozygosity if selection is sufficiently strong (cf. also Hedrick 1980).

In the absence of reliable public-health records, a retrospective analysis of the mechanisms and parameters underlying the spread of antimalarial drug resistance may be achieved indirectly through the patterns of selective sweeps. However, the analytical solution for the valley of reduced heterozygosity in the model of Schneider and Kim (2010) is not explicit, which limits their applicability. Moreover, it is not at all straightforward to interpret these results based on the model parameters.

In this article we derive accurate approximations to the exact, analytical solutions of Schneider and Kim (2010). The approximations under the assumption that the resistant allele is initially rare and that recombination is weak are similar to but different from the usual approximation for standard hitchhiking. Unlike in standard hitchhiking, our approximations are accurate even if the recombination rates are large and the resistant allele is initially not very rare. Moreover, using the approximations, we will show that incorporating host heterogeneity will result in an increased hitchhiking effect compared to our basic model, with corresponding selection parameters, which accounts just for one class of treated and one class of untreated hosts. The simple form of the approximations will allow us to easily interpret the effect of genetic hitchhiking in terms of the model parameters. Such approximations are extremely useful to achieve applicability of the results of Schneider and Kim (2010) to real data. Moreover, we show that the approximate solutions can be easily applied to identify the range of parameters that give rise to given levels of reduced heterozygosity in a given range of recombination distances. Finally, we discuss the differences compared with standard hitchhiking and give an outlook how our results can be applied to real data.

2 The model

We consider two biallelic loci. The first locus is subject to selection with a sensitive allele A_S and a resistant allele A_R segregating. The second locus is selectively neutral with the alleles N₁ and N₂ segregating. We will use the notation and parametrization summarized in Table 1.

Table 1.

Summary of notation

Haplotypes	ASN1	ASN2	ARN1	ARN2
Frequency	p1	p2	p3	p4
Fitness in	$W_1^{\left(U\right)}$	$W_2^{\left(U\right)}$	$W_3^{\left(U\right)}$	$W_4^{\left(U\right)}$
Untreated hosts	1	1	1 − s	1 − s
Fitness in	$W_1^{\left(T\right)}$	$W_2^{\left(T\right)}$	$W_3^{\left(T\right)}$	$W_4^{\left(T\right)}$
Treated hosts	1 − dS	1 − dS	1 − dR	1 − dR
Sensitive/resistant	Sen.	Sen.	Res.	Res.

The tables shows the notation of the four haplotypes, their frequencies, fitnesses in treated and untreated hosts, the parametrization of fitnesses that we are going to use for the illustrations in the following sections, and whether the haplotypes are sensitive or resistant. Here, s reflects metabolic costs of the resistant allele, while d_S and d_R indicate how efficiently the drug wipes out the sensitive and resistant parasites, respectively

Let p denote the frequency of the resistant allele A_R. We have p = p₃ + p₄. Furthermore, we denote the frequency of the neutral allele N₁ among the sensitive and resistant haplotypes by R and Q, respectively. We therefore have $R=\frac{p_1}{p_1+p_2}=\frac{p_1}{1-p}$ and $Q=\frac{p_3}{p_3+p_4}=\frac{p_3}{p}$.

Moreover, we denote the recombination rate between the two loci by r, and the vector of haplotype frequencies by p = (p₁, … , p₄). We assume that each host is infected randomly and independently by exactly m haploids (parasite strains). (We assume m to be a fixed parameter until Sect. 4.2, where we assume that m follows a fixed frequency-distribution).

Hosts acquire parasite strains according to their frequencies in the mosquito phase. Hence, the configuration of infections in hosts is multinomially distributed with parameters m and p₁, … , p₄. We assume that all haploids in a newly infected host have equal frequencies. Hence, the relative frequency of a haploid drawn from the parasite population among mosquitos is $\frac{1}{m}$. Let us denote a multi-index by m = (m₁, … , m₄), and the sum over its components by $\left|\mathit{m}\right|={\sum }_{i=1}^4{m}_i$. The probability that a host is infected by m_i copies of haplotype i (i = 1, … , n, |m| = m) is given by

$$\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right){\mathit{p}}^{\mathit{m}},$$ (1)

where $\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right)=\frac{m!}{{\prod }_{i=1}^4{m}_i!}$ denotes the respective multinomial coefficient and, as usual, ${\mathit{p}}^{\mathit{m}}:={\prod }_{i=1}^4{p}_i^{m_i}$.

After a host is infected the parasites reproduce clonally in the host. An infected host either receives drug treatment or is untreated. We assume that a fixed proportion α of infected hosts in the population is treated, whereas the remaining hosts are untreated. Thus, the probability for a host to be treated is simply α. The rate of reproduction of the haplotypes is different in treated and untreated hosts. The absolute fitness of a parasite strain is the expected number of its descendants in the host at the time of the mosquito visit. The absolute frequency (fitness) of haplotype i in an untreated host before a mosquito takes its blood meal is denoted by $\frac{m_i}{m}{W}_i^{(U)}$, whereas the absolute frequency of haplotype i in a treated host before a mosquito takes its blood meal is denoted by $\frac{m_i}{m}{W}_i^{(T)}$. [In the following, wherever it is appropriate, we use the superscript to (.) to resemble the superscripts (U) and (T).] Some of these haploids form gametocytes in male or female expressions. The frequencies of those are assumed to be proportional to the number of respective haplotypes. Furthermore, we impose that male and female gametocytes occur at the same frequencies. We assume that the number of different gametocytes taken by a mosquito during its blood meal from an infected host is proportional to its frequency in the host. Let γ denote the proportional constant, which is assumed to be the same for each mosquito. Hence, if the absolute frequencies of parasites in an infected host are $\frac{m_1}{m}{W}_1^{(.)},\dots ,\frac{m_4}{m}{W}_4^{(.)}$, the absolute frequencies of parasites absorbed during the blood meal are $\gamma \frac{m_1}{m}{W}_1^{(.)},\dots ,\gamma \frac{m_4}{m}{W}_4^{(.)}$. Note that this takes drug efficiency into account, because a mosquito will absorb a smaller number of parasites from a host in which drugs efficiently eliminated parasites.

In the mosquitos’ guts recombination occurs immediately after the blood meal during the phase in which meiosis occurs. In the gut of a mosquito, which has taken its blood meal from a host initially infected with m_i haplotypes i (i = 1, … , 4), the probability that a male k-gametocyte fertilizes a female l-gametocyte is

$$\frac{\gamma \frac{m_k}{m}{W}_k^{(.)}}{\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}}\cdot \frac{\gamma \frac{m_l}{m}{W}_l^{(.)}}{\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}}=\frac{m_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{W_{\mathit{m}}^{{(.)}^2}},$$

where

$$\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}=\frac{\gamma }{m}\sum _{k=1}^4{m}_k{W}_k^{(.)}$$

is the frequency of parasite haploids in the mosquito’s gut. The above probability is the relative frequency of a male k-gametocyte times that of a female l-gametocyte. Therefore, the absolute frequency of pairings of a male k-gametocyte and a female l-gametocyte is, the probability of such a fertilization times the absolute numbers of parasites in the gut, i.e.,

$$\frac{{\gamma }^2\frac{m_k}{m}{W}_k^{(.)}\frac{m_l}{m}{W}_l^{(.)}}{\frac{\gamma }{m}{W}_{\mathit{m}}^{(.)}}=\frac{\frac{\gamma }{m}{m}_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{W_{\mathit{m}}^{(.)}}.$$ (2)

The probability that a fertilization of a male k-gametocyte to a female l-gametocyte produces a haplotype i is denoted by R(kl → i). Therefore, the absolute frequencies of haplotype i in the population of mosquitos that took their blood meal from treated and untreated hosts are respectively

$$p_i^{\ast (.)}=\sum _{\left|\mathit{m}\right|=m}\left(\begin{array}{c}m\\ \mathit{m}\end{array}\right){\mathit{p}}^{\mathit{m}}\sum _{k,l=1}^4\frac{\gamma m_k{W}_k^{(.)}{m}_l{W}_l^{(.)}}{m{W}_{\mathit{m}}^{(.)}}R(\mathit{kl}\to i),$$

where the sum runs over all multi-indices $\mathit{m}\in {\mathrm{\mathbb{N}}}_{+}^4$ with |m| = m. Therefore, the relative frequencies of haplotypes in the mosquito population become

$$p_i^{\prime }=\frac{\alpha p_i^{\ast (T)}+(1-\alpha )p_i^{\ast (U)}}{\alpha {\sum }_{k=1}^4{p}_k^{\ast (T)}+(1-\alpha ){\sum }_{k=1}^4{p}_k^{\ast (U)}}=\frac{p_i^{\ast }}{{\sum }_{k=1}^4{p}_k^{\ast }},$$ (3a)

where

$$p_i^{\ast }:=\alpha p_i^{\ast (T)}+(1-\alpha )p_i^{\ast (U)}.$$ (3b)

For what follows, let us define the average fitness of the resistant allele among treated and untreated hosts by

$$\lambda :=\alpha W_3^{(T)}+(1-\alpha )W_3^{(U)}$$ (4a)

and that of the sensitive by

$$\mu :=\alpha W_1^{(T)}+(1-\alpha )W_1^{(U)}.$$ (4b)

If p(t) denotes the frequency of the resistant allele at time t, it changes according to $p(t)=\frac{{\lambda }^{t}p(0)}{{\lambda }^{t}p(0)+{\mu }^t(1-p(0))}$, i.e., according to the standard haploid one-locus selection model (cf. Schneider and Kim 2010). Thus, the resistant allele will sweep through the population if and only if λ > μ, otherwise it will get lost (or remain constant in frequency). Hence, in the following we will always assume λ > μ without further mentioning. Note that the spread of the resistant allele is independent from m. Moreover, it is obvious to calculate the time until a given level of resistance is reached (cf. Result 2 in Schneider and Kim 2010). Because of the relatively simple form of the dynamics of the resistant allele it is possible to derive simple conditions for the spread of resistance and its speed. Example 1 in Schneider and Kim (2010) directly links the fitness parameters to the spread of fixation. Furthermore, assuming that the fitnesses in treated hosts are functions of the administered drug concentration, Example 2 in Schneider and Kim (2010) illustrates the impact of the drug concentration and α on the spread of resistance and its speed. Assuming that the fitness of resistant parasites decays slower than that of the sensitive ones as a function of the drug concentration they found that resistance spreads most quickly for intermediate drug concentrations and large α.

Anyhow, the focus of this article is genetic hitchhiking. The following relations were derived in Schneider and Kim (2010).

$$\overline{W}{p}_i^{\prime }=p_i\left(\alpha W_i^{(T)}+(1-\alpha )W_i^{(U)}\right)+r_{i}p(1-p)(Q-R){\vartheta }_{p,m},$$ (5a)

where

$$\begin{array}{lll}{r}_1& =& -r_2=-r_3=r_4=r,\\ \overline{W}& =& p\lambda +(1-p)\mu ,\\ {\vartheta }_{p,m}& :=& \sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right){\theta }_{k,m}{p}^k{(1-p)}^{m-2-k},\end{array}$$ (5b)

$${\theta }_{k,m}:=\alpha {\theta }_{k,m}^{(T)}+(1-\alpha ){\theta }_{k,m}^{(U)},$$ (5c)

and

$${\theta }_{k,m}^{(.)}:=\frac{(m-1)W_1^{(.)}{W}_3^{(.)}}{(m-1-k)W_1^{(.)}+(k+1)W_3^{(.)}}.$$ (5d)

It was further shown in Schneider and Kim (2010) that

$$R^{\prime }=R+\mathit{rp}(Q-R)\frac{{\vartheta }_{p,m}}{\mu }$$ (6a)

and

$$Q^{\prime }=Q-r(1-p)(Q-R)\frac{{\vartheta }_{p,m}}{\lambda }.$$ (6b)

From the relations (5) and (6) the equilibrium frequency of the neutral allele N₁ was calculated to be

$${\widehat{Q}}^{(m)}=Q_0+\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }\frac{{\vartheta }_{p_{\tau },m}}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l},$$ (7)

where p₀, Q₀, and R₀ are the respective initial frequencies,

$${\vartheta }_{p_t,m}={\left(\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^t+1\right)}^{2-m}\sum _{k=0}^{m-2}\left(\begin{array}{c}m-2\\ k\end{array}\right){\theta }_{k,m}{\left(\frac{p_0}{1-p_0}\right)}^k{\left(\frac{\lambda }{\mu }\right)}^{\mathit{tk}},$$

and

$${\mathrm{\Lambda }}_{m,t}:=1-r\frac{{\vartheta }_{p_t,m}}{\lambda \mu }\left(\frac{p_0{\lambda }^{t+1}+(1-p_0){\mu }^{t+1}}{p_0{\lambda }^t+(1-p_0){\mu }^t}\right).$$ (8)

It was mentioned by Schneider and Kim (2010) that, for practical purposes, it suffices to sum (7) until the time of quasi-fixation, for which they provided an explicit formula. However, it is not at all obvious how Q̂^(m) is influenced by the various model parameters. In particular, when studying genetic hitchhiking using (7) it seems infeasible to predict the width of the valley of reduced heterozygosity in terms of the recombinational distance. Hence, simple but accurate approximations for (7) that permit a simple interpretation in terms of the model parameters are highly desirable.

3 Approximations

We shall now calculate simple approximations for (7). First, we treat the special case m = 2, and later deduce the general case from it.

3.1 Equilibrium frequencies at the neutral locus for m = 2

The equilibrium frequency of the neutral allele N₁ is given by

$$\widehat{Q}:={\widehat{Q}}^{(2)}=Q_0+\frac{r\vartheta (R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }\frac{{\prod }_{l=0}^{\tau -1}{\mathrm{\Lambda }}_l}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1},$$

where

$$\vartheta :={\vartheta }_{p_t,2}$$ (9)

is independent of the trajectory p_t of the resistant allele and in particular of p₀, and

$${\mathrm{\Lambda }}_l:={\mathrm{\Lambda }}_{2,l}.$$ (10)

In the following we will derive upper and lower bounds as well as approximations for Q̂ which exhibit a much simpler form. This permits us to explore the effects of the various parameters on Q̂.

First, note that Λ_l is monotone decreasing in l. To see this note that Λ_l < Λ_l−1 is equivalent to

$$1-r\frac{\vartheta }{\lambda \mu }\left(\frac{p_0{\lambda }^{l+1}+(1-p_0){\mu }^{l+1}}{p_0{\lambda }^l+(1-p_0){\mu }^l}\right)<1-r\frac{\vartheta }{\mathit{\lambda \mu }}\left(\frac{p_0{\lambda }^l+(1-p_0){\mu }^l}{p_0{\lambda }^{l-1}+(1-p_0){\mu }^{l-1}}\right).$$

This can be simplified to

$${\lambda }^{l-1}{\mu }^{l+1}+{\lambda }^{l+1}{\mu }^{l-1}>2{\lambda }^l{\mu }^l.$$

By dividing through λ^l−1 μ^l−1 this simplifies to

$${(\lambda -\mu )}^2>0.$$

Moreover, note that

$$\underset{¯}{\mathrm{\Lambda }}:=\underset{l\to \infty }{\lim }{\mathrm{\Lambda }}_l=\underset{l\to \infty }{\lim }1-r\frac{\vartheta }{\mathit{\lambda \mu }}\left(\frac{p_0\lambda +(1-p_0)\mu {\left(\frac{\mu }{\lambda }\right)}^l}{p_0+(1-p_0){\left(\frac{\mu }{\lambda }\right)}^l}\right)=1-r\frac{\vartheta }{\mu }.$$ (11)

Hence, by using

$$\overline{\mathrm{\Lambda }}:=\mathrm{\Lambda }(0)=1-\frac{r\vartheta (p_0\lambda +(1-p_0)\mu )}{\lambda \mu }\ge {\mathrm{\Lambda }}_l\ge \underset{¯}{\mathrm{\Lambda }},$$ (12)

we obtain

$${\overline{\mathrm{\Lambda }}}^{\tau }\ge \prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_l\ge {\underset{¯}{\mathrm{\Lambda }}}^{\tau }.$$

Furthermore, because λ > μ we have

$$1-\frac{r\vartheta (p_0\lambda +(1-p_0)\mu )}{\lambda \mu }\le 1-\frac{r\vartheta (p_0\mu +(1-p_0)\mu )}{\lambda \mu }=1-\frac{r\vartheta }{\lambda }=:\stackrel{\sim }{\mathrm{\Lambda }},$$ (13)

and consequently Λ̃ ≥ Λ̅.

Let us define

$$Q^{(a)}:=Q_0+\frac{r\vartheta (R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }\frac{a^{\tau }}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}.$$ (14)

Note that by relabeling the alleles, we can assume without loss of generality that R₀ > Q₀. Hence, (14) is monotone increasing in a. Thus, we can formulate our first result.

Result 1

Let Q^(a) be defined as in (14). Then, Q^(a) is monotone increasing in a. Moreover, let Λ̲, Λ̅ and Λ̃ be defined as in (11), (12), and (13), respectively. Then

$$\overline{Q}:=Q^{(\overline{\mathrm{\Lambda }})}\mathit{and}\stackrel{\sim }{Q}:=Q^{(\stackrel{\sim }{\mathrm{\Lambda }})}$$

are upper bounds for Q̂, and

$$\underset{¯}{Q}:=Q^{(\underset{¯}{\mathrm{\Lambda }})}$$

is a lower bound for Q̂.

Although the expressions of this bounds are simpler than that of Q̂ they are still not very explicit. Hence, we shall derive upper and lower bounds for Q̅ and Q̲, or more generally for Q^(a).

First, note that ϑ < λ. This is because it is equivalent to

$$\alpha W_3^{(T)}+(1-\alpha )W_3^{(U)}>\frac{\alpha W_1^{(T)}{W}_3^{(T)}}{W_1^{(T)}+W_3^{(T)}}+\frac{(1-\alpha )W_1^{(U)}{W}_3^{(U)}}{W_1^{(U)}+W_3^{(U)}}$$

which obviously holds because

$$\frac{W_1^{(T)}}{W_1^{(T)}+W_3^{(T)}}<1\mathrm{and}\frac{W_1^{(U)}}{W_1^{(U)}+W_3^{(U)}}<1.$$

Essentially the same calculation shows ϑ < μ. Therefore, we have $\frac{\vartheta }{\lambda }<1$ and $\frac{\vartheta }{\mu }<1$. This combined with (11) and (13) implies $\frac{1}{2}<\underset{¯}{\mathrm{\Lambda }}<\stackrel{\sim }{\mathrm{\Lambda }}\le 1$,since $r\in [0,\frac{1}{2}]$. Hence, in the following we will always assume $a\in [\underset{¯}{\mathrm{\Lambda }},\stackrel{\sim }{\mathrm{\Lambda }}]\subseteq [\frac{1}{2},1]$.

Notice that Q̃ has exactly the same form as in the standard haploid hitchhiking model derived by Maynard Smith and Haigh (1974; eq. 8), with r replaced by $\frac{\vartheta r}{\lambda }$ and p₀ replaced by $\frac{\mu p_0}{\lambda (1-p_0)+\mu p_0}$. Thus, we can interpret this as studying standard hitchhiking with an ‘effective’ recombination rate $\frac{\vartheta r}{\lambda }$, which is smaller than r, and an ‘effective’ initial frequency of $\frac{\mu p_0}{\lambda (1-p_0)+\mu p_0}$, which is smaller than the actual initial frequency. The adjusted recombination rate leads to a more severe hitchhiking effect, whereas the adjusted initial frequency leads to a less pronounced hitchhiking effect. Combination of this factors lead to a more severe hitchhiking effect (cf. Schneider and Kim 2010).

Next, we need two definitions. For a ∈ ℝ and k ∈ ℕ⁺ the upper Pochhammer symbol is defined by

$${(a)}_{\overline{k}}:=\prod _{l=0}^{k-1}(a+l).$$

The hypergeometric function is defined by

$${}_r\mathrm{F}_s\left(\begin{array}{c}{a}_1,\dots ,a_r\\ b_1,\dots ,b_s\end{array}\mid z\right):=\sum _{k=0}^{\infty }\frac{z^k}{k!}\frac{{\prod }_{u=1}^r{(au)}_{\overline{k}}}{{\prod }_{\upsilon =1}^s(b_{\upsilon })\overline{k}},$$

where r, s ∈ ℕ, z, a₁, …, a_r ∈ ℝ, b₁, … , $b_s\in \mathrm{ℝ}\backslash {\mathbb{Z}}_0^{-}$.

With the above definition we are already able to formulate our first theorem.

Theorem 1

Assume $a\ne {(\frac{\mu }{\lambda })}^l$ for l ∈ ℕ, and let csc $x=\frac{1}{\sin x}$ denote the cosecant of x. If $p_0<\frac{1}{2}$, the function

$$\psi (a):=Q_0+\frac{\mathit{r\vartheta }(R_0-Q_0)}{\lambda }[\frac{\pi \csc \left(\frac{\pi \log a}{\log \lambda -\log \mu }\right)}{(\log \lambda -\log \mu ){\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \lambda -\log \mu }}}-\frac{1}{\log a}{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\log a}{\log \lambda -\log \mu }\\ 1+\frac{\log a}{\log \lambda -\log \mu }\end{array}\mid \frac{-p_0}{1-p_0}\right)]$$ (15)

is a lower bound for Q^(a). If $p_0<\frac{\lambda }{\lambda +\mu }$,

$$\mathrm{\Psi }(a):=Q_0+\frac{\mathit{r\vartheta }(R_0-Q_0)}{\lambda }[\frac{\pi \csc \left(\frac{\pi \log a}{\log \lambda -\log \mu }\right)}{(\log \lambda -\log \mu ){\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \lambda -\log \mu }}}-\frac{1}{a\log a}{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\log a}{\log \lambda -\log \mu }\\ 1+\frac{\log a}{\log \lambda -\log \mu }\end{array}\mid \frac{p_0\mu }{(1-p_0)\lambda }\right)]$$ (16)

is an upper bound for Q^(a).

Proof

Consider the function

$$g(x)=\frac{a^x}{{\mathit{cb}}^x+1}$$ (17)

for x > −1 with a ∈ (0, 1), and let

$$b:=\frac{\lambda }{\mu }>1,\mathrm{and}c:=\frac{p_0}{1-p_0}.$$ (18)

By calculating the derivative, which is given by

$$g^{\prime }(x)=\frac{a^x(\log a+{\mathit{cb}}^x(\log a-\log b))}{{(1+{\mathit{cb}}^x)}^2}$$

and obviously always negative, we recognize that g is monotone decreasing as a function in x. Thus, we obtain the estimate

$$\underset{0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x\le \sum _{\tau =0}^{\infty }g(\tau )\le \underset{0}{\overset{\infty }{\mathit{\int }}}g(x-1)\mathrm{d}x=\underset{-1}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x.$$ (19)

Since, we have

$$Q^{(a)}=Q_0+\frac{r\vartheta (R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }g(\tau ),$$

it follows from (19) that

$$\psi (a)=Q_0+\frac{r\vartheta (R_0-Q_0)}{\lambda }\underset{0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x$$ (20)

is a lower bound for Q^(a), and that

$$\mathrm{\Psi }(a)=Q_0+\frac{r\vartheta (R_0-Q_0)}{\lambda }\underset{-1}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x$$ (21)

is an upper bound for Q^(a).

We will now manipulate the above equations. First, rewrite g as

$$g(x)=\frac{e^{\mathit{x\xi }}}{1+{\mathit{ce}}^{\mathit{x\eta }}},$$ (22)

where

$$\xi :=\log a\mathrm{and}\eta :=\log b.$$ (23)

Assume first that ce^xη < 1. Hence, g is a geometric series, can be rewritten as

$$g(x)=e^{\mathit{x\xi }}\sum _{k=0}^{\infty }{(-{\mathit{ce}}^{\mathit{x\eta }})}^k=\sum _{k=0}^{\infty }{(-c)}^k{e}^{x(\xi +\mathit{k\eta })},$$ (24)

and converges absolutely for all x satisfying ce^xη < 1. If ce^xη > 1, we have $\frac{1}{{\mathit{ce}}^{\mathit{x\eta }}}<1$ and can expand (22) into the power series

$$g(x)=\frac{e^{\mathit{x\xi }}}{{\mathit{ce}}^{\mathit{x\eta }}}\frac{1}{1-\frac{-1}{{\mathit{ce}}^{\mathit{x\eta }}}}=\frac{e^{\mathit{x\xi }}}{{\mathit{ce}}^{\mathit{x\eta }}}\sum _{k=0}^{\infty }{(-{\mathit{ce}}^{\mathit{x\eta }})}^{-k}=-\sum _{k=0}^{\infty }{(-c)}^{-(k+1)}{e}^{x(-\eta (k+1)+\xi )},$$

which converges absolutely for all x satisfying ce^xη > 1.

Let us further define $x_0:=-\frac{\log c}{\log b}$. The assumption $p_0<\frac{1}{2}$ guarantees x₀ > 0. The absolute convergence of the above series enables us to integrate by summands, i.e., for x < x₀ we have

$$\begin{array}{lll}{G}_1(x)& =& \mathit{\int }g(x)\mathrm{d}x=\mathit{\int }\sum _{k=0}^{\infty }{(-c)}^k{e}^{x(\mathit{\eta k}+\xi )}\mathrm{d}x=\sum _{k=0}^{\infty }\mathit{\int }{(-c)}^k{e}^{x(\mathit{\eta k}+\xi )}\mathrm{d}x\end{array}$$ (25a)

$$\begin{array}{ll}=& \sum _{k=0}^{\infty }{(-c)}^k\frac{e^{x(\mathit{\eta k}+\xi )}}{\mathit{\eta k}+\xi }=\frac{e^{\mathit{x\xi }}}{\eta }\sum _{k=0}^{\infty }{(-c)}^k\frac{e^{\mathit{x\eta k}}}{k+\frac{\xi }{\eta }}\\ =& \frac{e^{x\xi }}{\xi }\sum _{k=0}^{\infty }\frac{\frac{\xi }{\eta }}{k+\frac{\xi }{\eta }}{(-{\mathit{ce}}^{\mathit{x\eta }})}^k\end{array}$$ (25b)

$$=\frac{e^{\mathit{x\xi }}}{\xi }\sum _{k=0}^{\infty }\frac{{\left(\frac{\xi }{\eta }\right)}_{\overline{k}}{(1)}_{\overline{k}}}{{\left(1+\frac{\xi }{\eta }\right)}_{\overline{k}}}\frac{{(-{\mathit{ce}}^{\mathit{x\eta }})}^k}{k!}=\frac{e^{\mathit{x\xi }}}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -{\mathit{ce}}^{\mathit{x\eta }}\right).$$ (25c)

Note that we have used the fact that $\frac{\xi }{\eta }\ne -k$ for all k ∈ ℕ in (25b), which is guaranteed by the assumption $a\ne {(\frac{\mu }{\lambda })}^k$ for all k ∈ ℕ.

Similarly, for x > x₀ we have

$$\begin{array}{lll}{G}_2(x)& =& \mathit{\int }g(x)\mathrm{d}x=\mathit{\int }-\sum _{k=0}^{\infty }{(-c)}^{-(k+1)}{e}^{x(-\eta (k+1)+\xi )}\mathrm{d}x\\ & =& -\sum _{k=0}^{\infty }\mathit{\int }{(-c)}^{-(k+1)}{e}^{x(-\eta (k+1)+\xi )}\mathrm{d}x\end{array}$$ (26a)

$$\begin{array}{ll}=& -\sum _{k=0}^{\infty }{(-c)}^{-(k+1)}\frac{e^{x(-\eta (k+1)+\xi )}}{-\eta (k+1)+\xi }\\ =& \frac{e^{x\xi }}{\eta }\sum _{k=0}^{\infty }{(-c)}^{-(k+1)}\frac{e^{-x\eta (k+1)}}{-(k+1)+\frac{\xi }{\eta }}\end{array}$$ (26b)

$$=\frac{-e^{\mathit{x\xi }}}{\eta }\sum _{k=1}^{\infty }{(-c)}^{-k}\frac{e^{-x\eta k}}{-k+\frac{\xi }{\eta }}=\frac{-e^{\mathit{x\xi }}}{\xi }\sum _{k=1}^{\infty }\frac{-\frac{\xi }{\eta }}{k-\frac{\xi }{\eta }}{\left(\frac{-1}{c{e}^{\mathit{x\eta }}}\right)}^k$$ (26c)

$$\begin{array}{cc}=& \frac{-e^{\mathit{x\xi }}}{\xi }\sum _{k=1}^{\infty }\frac{{\left(-\frac{\xi }{\eta }\right)}_{\overline{k}}{(1)}_{\overline{k}}}{{\left(1-\frac{\xi }{\eta }\right)}_{\overline{k}}}\frac{{\left(\frac{-1}{c{e}^{x\eta }}\right)}^k}{k!}\\ =& \frac{e^{x\xi }}{\xi }\left[1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,-\frac{\xi }{\eta }\\ 1-\frac{\xi }{\eta }\end{array}\mid -\frac{1}{c{e}^{\mathit{x\eta }}}\right)\right].\end{array}$$ (26d)

It should be mentioned that we did not need the assumption $a\ne {(\frac{\mu }{\lambda })}^k$ for all k ∈ ℕ in (26).

Next, assume $p_0<\frac{1}{2}$ i.e., x₀ > 0. Hence, we have

$$\begin{array}{lll}\underset{0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x& =& \underset{0}{\overset{x_0}{\mathit{\int }}}g(x)\mathrm{d}x+\underset{x_0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x\\ & =& \underset{x\to x_0-}{\lim }{G}_1(x)-G_1(0)+\underset{x\to +\infty }{\lim }{G}_2(x)-\underset{x\to x_0+}{\lim }{G}_2(x).\end{array}$$

Since $\frac{1}{k+\frac{\xi }{\eta }}\to 0$, the Leibnitz criterium implies that

$$G_1(x_0)=\frac{e^{-\frac{\xi \log c}{\eta }}}{\eta }\sum _{k=0}^{\infty }\frac{{(-1)}^k}{k+\frac{\xi }{\eta }}$$ (27)

converges, i.e., −∞ < G₁(x₀) < ∞. Furthermore, by a similar argument we obtain −∞ < G₂(x₀) < ∞. We also see that

$$\begin{array}{ccc}|G_2(x)|& =& \left|\frac{-e^{\mathit{x\xi }}}{\eta }\sum _{k=1}^{\infty }{(-c)}^{-k}\frac{e^{-\mathit{x\eta k}}}{-k+\frac{\xi }{\eta }}\right|\le \frac{e^{\mathit{x\xi }}}{\eta }\sum _{k=1}^{\infty }\left|{(-c)}^{-k}\frac{e^{-\mathit{x\eta k}}}{-k+\frac{\xi }{\eta }}\right|\\ & =& \frac{e^{\mathit{x\xi }}}{\eta }\sum _{k=1}^{\infty }{\left|\frac{1}{{\mathit{ce}}^{\mathit{x\eta }}}\right|}^k\frac{1}{k-\frac{\xi }{\eta }}\le \frac{e^{x\xi }}{\eta }\sum _{k=1}^{\infty }{\left|\frac{1}{{\mathit{ce}}^{\mathit{x\eta }}}\right|}^k=\frac{e^{\mathit{x\xi }}}{\eta (1-c{e}^{\mathit{x\eta }})}.\end{array}$$

Hence, for x > x₀ this implies that the series representation (26d) of G₂(x) is absolute convergent. Therefore, we obtain

$$\underset{x\to x_0+}{\lim }{G}_2(x)=G_2(x_0)$$ (28)

and

$$\underset{x\to +\infty }{\lim }{G}_2(x)=\frac{0}{\xi }\left[1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,-\frac{\xi }{\eta }\\ 1-\frac{\xi }{\eta }\end{array}\mid 0\right)\right]=0.$$ (29)

Similarly, we see that G₁(x) is absolute convergent for x₀ < x. Therefore, we have

$$\underset{x\to x_0-}{\lim }{G}_1(x)=G_1(x_0).$$ (30)

We obtain

$$\begin{array}{lll}\underset{0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x& =& G_1(x_0)-G_1(0)-G_2(x_0)\\ & =& \frac{e^{-\frac{\xi \log c}{\eta }}}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -1\right)-\frac{1}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -c\right)-\frac{e^{-\frac{\xi \log c}{\eta }}}{\xi }\left[1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,-\frac{\xi }{\eta }\\ 1-\frac{\xi }{\eta }\end{array}\mid -1\right)\right].\end{array}$$ (31)

If $p_0<\frac{\lambda }{\lambda +\mu }$, we have x₀ > − 1. The above calculations are still valid and yield

$$\begin{array}{lll}\underset{-1}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x& =& G_1(x_0)-G_1(-1)-G_2(x_0)\\ & =& \frac{e^{-\frac{\xi \log c}{\eta }}}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -1\right)-\frac{e^{-\xi }}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -{\mathit{ce}}^{-\eta }\right)-\frac{e^{-\frac{\xi \log c}{\eta }}}{\xi }\left[1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,-\frac{\xi }{\eta }\\ 1-\frac{\xi }{\eta }\end{array}\mid -1\right)\right].\end{array}$$ (32)

Let us now simplify (31) and (32). Note that

$$\begin{array}{lll}A& :=& {}_2\mathrm{F}_1\left(\begin{array}{c}1,\kappa \\ 1+\kappa \end{array}\mid -1\right)+{}_2\mathrm{F}_1\left(\begin{array}{c}1,-\kappa \\ 1-\kappa \end{array}\mid -1\right)\\ & =& \sum _{k=0}^{\infty }\frac{{(1)}_{\overline{k}}{(\kappa )}_{\overline{k}}}{{(\kappa +1)}_{\overline{k}}}\frac{{(-1)}^k}{k!}+\sum _{k=0}^{\infty }\frac{{(1)}_{\overline{k}}{(-\kappa )}_{\overline{k}}}{{(-\kappa +1)}_{\overline{k}}}\frac{{(-1)}^k}{k!}\\ & =& \sum _{k=0}^{\infty }\frac{{(-1)}^k\kappa }{\kappa +k}+\sum _{k=0}^{\infty }\frac{-{(-1)}^k\kappa }{-\kappa +k}=\sum _{k=0}^{\infty }\frac{2{\kappa }^2{(-1)}^k}{k^2-{\kappa }^2}\\ & =& 2{\kappa }^2{\pi }^2\sum _{k=0}^{\infty }\frac{{(-1)}^k}{{\kappa }^2{\pi }^2-k^2{\pi }^2}.\end{array}$$

By using the the well known series

$$\csc (z)=-\frac{1}{z}+2z\sum _{k=0}^{\infty }\frac{{(-1)}^k}{z^2-k^2{\pi }^2}\mathrm{for}\frac{z}{\pi }\notin \mathrm{\mathbb{Z}},$$

we arrive at

$$A=\pi \kappa \csc (\pi \kappa )-1.$$

Because $a\ne {(\frac{\mu }{\lambda })}^k$ for k ∈ ℕ we have $\frac{\xi }{\eta }\notin {\mathrm{\mathbb{Z}}}^{+}$. Because, we assume a ∈ [0, 1] and λ > μ we also have $a\ne {\left(\frac{\mu }{\lambda }\right)}^k$ for k ∈ ℤ⁻. Hence, we have $\frac{\xi }{\eta }\notin \mathrm{\mathbb{Z}}$. Therefore, we obtain

$$\underset{0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x=\frac{\pi \csc (\pi \frac{\xi }{\eta })}{{\mathit{\eta c}}^{\frac{\xi }{n}}}-\frac{1}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -c\right)$$

and

$$\underset{-1}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x=\frac{\pi \csc (\pi \frac{\xi }{\eta })}{{\mathit{\eta c}}^{\frac{\xi }{\eta }}}-\frac{e^{-\xi }}{\xi }{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -{\mathit{ce}}^{-\eta }\right).$$

Combining the above with (20) and (21) and the definitions of ξ, η, and c immediately yields (15) and (16).

The assumptions $p_0<\frac{1}{2}$, or $p_0<\frac{\lambda }{\lambda +\mu }$ hold whenever one aims to study the hitchhiking effect of a mutation that is initially rare. If the initial frequency of the mutation is not rare because one is interesting in studying mutations from standing genetic variation that become beneficial, for instance, because of a change in the environment, i.e., if one wants to study soft selective sweeps (cf. Hermisson and Pennings 2005), Theorem 1 is not applicable. The study of soft selective sweeps is relevant and hence we shall also treat the cases $p_0\ge \frac{1}{2}$ and $p_0\ge \frac{\lambda }{\lambda +\mu }$.

Remark 1

The proof of Theorem 1 reveals that we have to replace (15) by

$$\psi \left(a\right)=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda \log a}\left[1-{}_2\mathrm{F}_1\left(\begin{array}{l}1,\frac{\log a}{\log \mu -\log \lambda }\\ 1+\frac{\log a}{\log \mu -\log \lambda }\end{array}\mid -\frac{1-p_0}{p_0}\right)\right]$$ (33)

if $p_0\ge \frac{1}{2}$. Moreover, we have to replace (16) by

$$\mathrm{\Psi }\left(a\right)=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\mathit{\lambda a}\log a}\left[1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\log a}{\log \mu -\log \lambda }\\ 1+\frac{\log a}{\log \mu -\log \lambda }\end{array}\mid -\frac{(1-p_0)\lambda }{p_0\mu }\right)\right]$$ (34)

if $p_0\ge \frac{\lambda }{\lambda +\mu }$. Notably, (33) and (34) also hold if $a={\left(\frac{\lambda }{\mu }\right)}^k$ for k ∈ ℕ. Furthermore, (33) and (34) are the continuations of (15) and (16) as functions in p₀.

Theorem 1 assumes $a\ne {\left(\frac{\lambda }{\mu }\right)}^k$ for all k ∈ ℕ. If this assumption is violated we have to make the following adjustments.

Remark 2

Assume l ∈ ℕ. If $p_0<\frac{1}{2}$,

$$\psi \left({\left(\frac{\mu }{\lambda }\right)}^l\right)=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda \left(\log \mu -\log \lambda \right)}\left[\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}{\left(\frac{p_0}{1-p_0}\right)}^k-{\left(\frac{-p_0}{1-p_0}\right)}^l\log p_0\right],$$ (35)

is a lower bound for $Q^{({(\frac{\mu }{\lambda })}^l)}$. If $p_0<\frac{\lambda }{\lambda +\mu }$,

$$\mathrm{\Psi }\left({\left(\frac{\mu }{\lambda }\right)}^l\right)=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda \left(\log \mu -\log \lambda \right)}\left[\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}{\left(\frac{\mu }{\lambda }\right)}^{k-l}{\left(\frac{p_0}{1-p_0}\right)}^k-{\left(\frac{-p_0}{1-p_0}\right)}^l\log \left(\frac{p_0\mu }{p_0\mu +\left(1-p_0\right)\lambda }\right)\right]$$ (36)

is an upper bound for $Q^{({(\frac{\mu }{\lambda })}^l)}$. Moreover, (35) and (36) are the continuations of (15) and (16) in the limit $a\to {\left(\frac{\mu }{\lambda }\right)}^l$. If $p_0\ge \frac{1}{2}$, (35) has to be replaced by (33). If $p_0\ge \frac{\mathrm{\lambda }}{\lambda +\mu }$, (36) has to be replaced by (34).

The proof can be found in Appendix A.1.

Let

$$\stackrel{\sim }{\mathrm{\Psi }}:=\mathrm{\Psi }\left(\stackrel{\sim }{\mathrm{\Lambda }}\right),\overline{\mathrm{\Psi }}:=\mathrm{\Psi }\left(\overline{\mathrm{\Lambda }}\right),\mathrm{and}\underset{¯}{\mathrm{\Psi }}:=\mathrm{\Psi }\left(\underset{¯}{\mathrm{\Lambda }}\right)$$ (37)

and analogously

$$\stackrel{\sim }{\psi }:=\psi \left(\stackrel{\sim }{\mathrm{\Lambda }}\right),\overline{\psi }:=\psi \left(\overline{\mathrm{\Lambda }}\right),\mathrm{and}\underset{¯}{\psi }:=\psi \left(\underset{¯}{\mathrm{\Lambda }}\right).$$ (38)

We immediately obtain the following corollary.

Corollary 1

We have Ψ̃ ≥ Ψ̅ ≥ Q̅ ≥ Q̂ ≥ ψ̲, hence Ψ̃ and Ψ̅ are upper bounds for Q̂, and ψ̲ is a lower bound for Q̂. Moreover, we have Ψ̃ ≥ Q̃ ≥ ψ̃, Ψ̅ ≥ Q̅ ≥ ψ̅, and Ψ̲ ≥ Q̲ ≥ ψ̲.

Figure 1 illustrates Q̂ and its bounds Q̲ and Q̅, as well as their bounds Ψ̅, Ψ̲, ψ̅, and ψ̲ for various parameters. It becomes obvious that the upper bound Q̅ is very close to Q̂, whereas the lower bound Q̲ greatly underestimates Q̂.

Fig. 1.

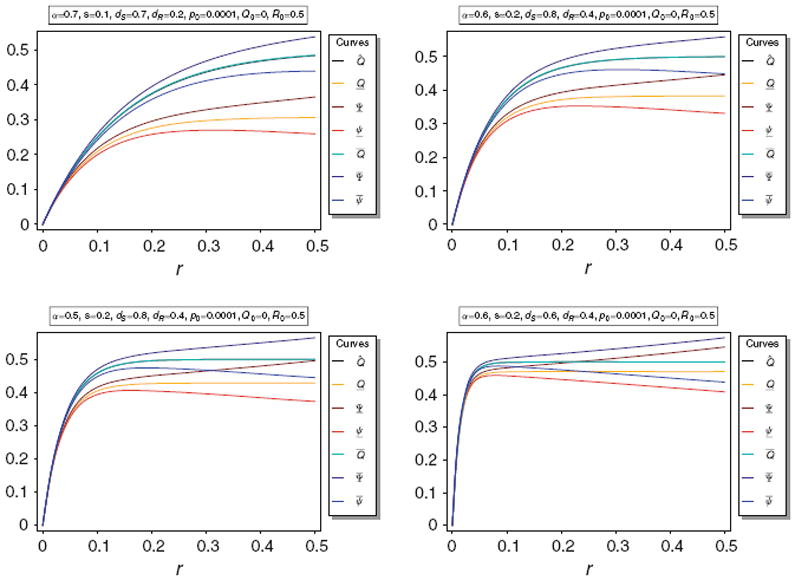
Equilibrium frequency Q̂ of the neutral allele N₁ and various bounds for Q̂ as a function of r for different parameter combinations. The panels show Q̂ along with its upper and lower bounds Q̅ and Q̲, as well as their respective upper and lower bounds Ψ̅ and ψ̅, and Ψ̲ and ψ̲. The parameters for the various plot panels are specified in the boxes above the panels. In all panels Q̂ and Q̅ are almost identical

It turns out that Q̃ and Q̅ are almost identical unless p₀ is large. The same holds for for Ψ̃ and Ψ̅. This is illustrated in Fig. 2.

Fig. 2.

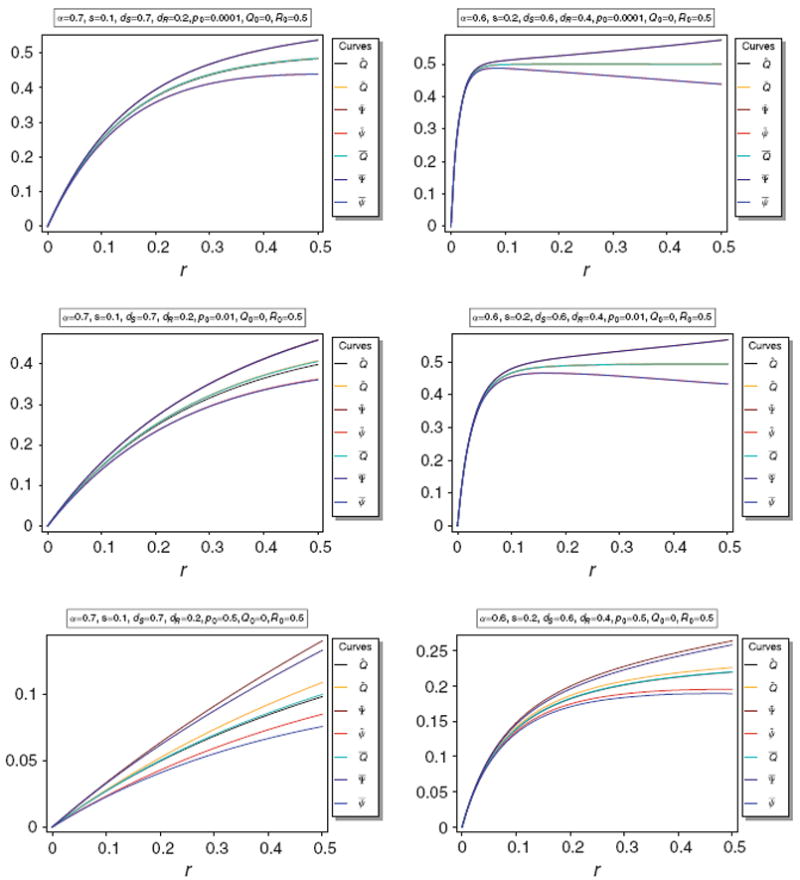
Equilibrium frequency Q̂ of the neutral allele N₁ and various bounds of Q̂ as a function of r for different parameter combinations. The panels show Q̂ along with its upper bounds Q̅ and Q̃, as well as their respective upper and lower bounds Ψ̅ and ψ̅, and Ψ̲ and ψ̲. The parameters for the various plot panels are specified in the boxes above the panels

Although, Ψ (a) and ψ(a) have closed expressions, these expressions involve the hypergeometric function. In the following we shall derive approximations for Ψ(a) and ψ(a) that make no use of the hypergeometric function. Our first step is the following theorem.

Theorem 2

For $p_0<\frac{1}{2}$ let

$$\varphi \left(a\right):=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda }\left[{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}\left(\frac{1}{\log a}-\frac{1}{\log a+\log \lambda -\log \mu }+\frac{1}{\log a-\log \lambda +\log \mu }\right)-\frac{1}{\log a}+\frac{p_0}{\left(\log a+\log \lambda -\log \mu \right)(1-p_0)}\right]$$ (39)

and, for $p_0<\frac{\lambda }{\lambda +\mu }$ let

$$\mathrm{\Phi }\left(a\right):=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda }\left[{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}\left(\frac{1}{\log a}-\frac{1}{\log a+\log \lambda -\log \mu }+\frac{1}{\log a-\log \lambda +\log \mu }\right)-\frac{1}{a\log a}+\frac{p_{0\mu }}{a\left(\log a+\log \lambda -\log \mu \right)(1-p_0)\lambda }\right].$$ (40)

If $p_0<\frac{1}{2}$, ϕ(a) ≈ ψ(a) and if $p_0<\frac{\lambda }{\lambda +\mu }$, Φ(a) ≈ Ψ (a).

The proof can be found in Appendix A.1.

If $p_0\ge \frac{1}{2}$, or $p_0\ge \frac{\lambda }{\lambda +\mu }$ we have to modify the definitions of ϕ(a), or Φ(a), respectively.

Remark 3

For $p_0\ge \frac{1}{2}$ let

$$\varphi \left(a\right):=Q_0-\frac{r\vartheta \left(R_0-Q_0\right)\left(1-p_0\right)}{\lambda p_0\left(\log \lambda -\log \mu -\log a\right)}$$ (41)

and, for $p_0\ge \frac{\lambda }{\lambda +\mu }$ let

$$\mathrm{\Phi }\left(a\right):=Q_0-\frac{r\vartheta \left(R_0-Q_0\right)\left(1-p_0\right)}{\mu p_0\left(\log \lambda -\log \mu -\log a\right)}.$$ (42)

If $p_0\ge \frac{1}{2}$, ϕ(a) ≈ ψ(a) and if $p_0\ge \frac{\lambda }{\lambda +\mu }$, Φ(a) ≈ Ψ(a). Moreover, (41) and (42) are the continuations of (39) and (40) regarded as functions in p₀.

The proof can be found in Appendix A.1.

From Theorem 2, Remark 3, and the definitions of Λ̲, Λ̅, and Λ̃ we immediately obtain the following corollary.

Corollary 2

Let Ψ, ψ, Φ and ϕ be defined as in Theorems 1 and 2, and Remarks 1–3. Furthermore, let

$$\stackrel{\sim }{\mathrm{\Phi }}:=\mathrm{\Phi }(\stackrel{\sim }{\mathrm{\Lambda }}),\overline{\mathrm{\Phi }}:=\mathrm{\Phi }(\overline{\mathrm{\Lambda }}),\underset{¯}{\mathrm{\Phi }}:=\mathrm{\Phi }(\underset{¯}{\mathrm{\Lambda }})$$ (43)

and

$$\stackrel{\sim }{\varphi }:=\varphi (\stackrel{\sim }{\mathrm{\Lambda }}),\overline{\varphi }:=\varphi (\overline{\mathrm{\Lambda }}),\underset{¯}{\varphi }:=\varphi (\underset{¯}{\mathrm{\Lambda }}).$$ (44)

Then Φ̃ ≈ Ψ̃, Φ̅ ≈ Ψ̅, Φ̲ ≈ Ψ̲, ϕ̃ ≈ ψ̃, ϕ̅ ≈ ψ̅, and ϕ̲ ≈ ψ̲.

The approximations provided in Corollary 2 are very accurate unless p₀ becomes too large. This is illustrated in Fig. 3.

Fig. 3.

Equilibrium frequency Q̂ of the neutral allele N₁ and various bounds of Q̂ as a function of r for different parameter combinations. The panels show Q̂ along with its upper bounds Q̅ and Q̃, as well as their respective upper and lower bounds Ψ̅ and ψ̅, and Ψ̃ and ψ̃, along with their approximations Φ̅ and ϕ̅, and Φ̃ and ϕ̃, respectively. The parameters for the various plot panels are specified in the boxes above the panels

Note that we derived the upper and lower bounds for Q^(a) by using the estimate (19). However, we can use (19) for the standard estimate

$$\sum _{k=0}^{\infty }g(k)\approx \frac{1}{2}\underset{-1}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x+\frac{1}{2}\underset{0}{\overset{\infty }{\mathit{\int }}}g(x)\mathrm{d}x.$$ (45)

Hence, the estimates summarized in the next corollary follow immediately.

Corollary 3

Estimates for Q̂ are given by

$${\overline{Q}}^{\ast }:=\frac{1}{2}(\overline{\mathrm{\Psi }}+\overline{\psi })\mathrm{and}{\stackrel{\sim }{Q}}^{\ast }:=\frac{1}{2}(\stackrel{\sim }{\mathrm{\Psi }}+\stackrel{\sim }{\psi }),$$ (46)

and

$${\overline{Q}}^{\circ }:=\frac{1}{2}(\overline{\mathrm{\Phi }}+\overline{\varphi })\mathrm{and}{\stackrel{\sim }{Q}}^{\circ }=\frac{1}{2}(\stackrel{\sim }{\mathrm{\Phi }}+\stackrel{\sim }{\varphi }).$$ (47)

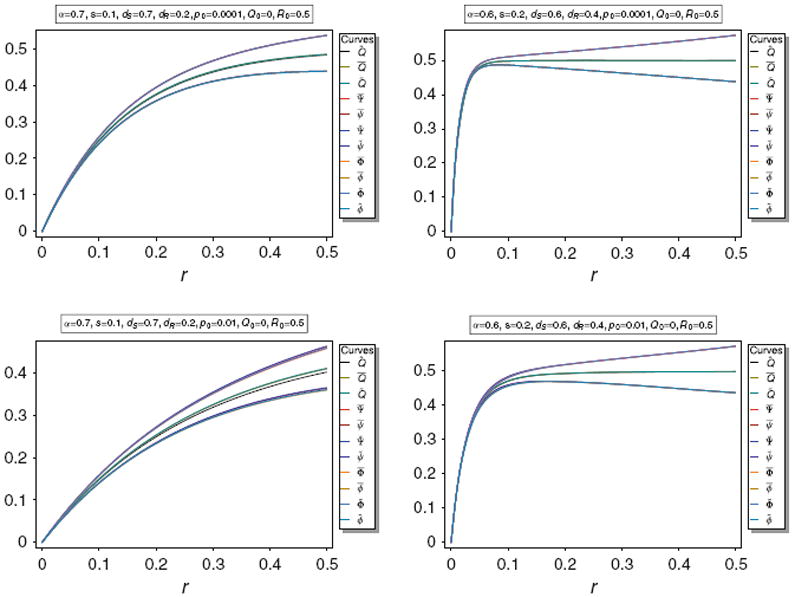
The approximations of Corollary 3 are illustrated in Fig. 4. It is obvious that the above approximations are very accurate for various parameters.

Fig. 4.

Equilibrium frequency Q̂ of the neutral allele N₁ and various bounds of Q̂ as a function of r for different parameter combinations. The panels show Q̂ along with its upper bounds Q̅ and Q̃, as well as its approximations Q̅*, Q̃*, Q̅°, and Q̃°. The parameters are the same as in Fig. 3

Although we already arrived at relatively simple approximations for Q̂, they are still difficult to interpret in terms of the involved parameters. In the following we will concentrate on the case in which the initial frequency p₀ of the resistant allele is small. This is the most relevant case for studying genetic hitchhiking.

3.2 Approximations for rare mutations

So far in our derivations we did not assume that the initial frequency p₀ of the resistant allele is small. However, since this is the biologically most relevant situations we shall derive further approximations for the equilibrium frequencies of the neutral alleles under the assumption that the mutation is initially rare, i.e., p₀ ≈ 0 and 1 − p₀ ≈ 1. Since we have Λ̃ ≈ Λ̅ under this assumption we focus on estimates based on Λ̃.

For p₀ ≈ 0 we obtain the following theorem.

Theorem 3

Let

$$A\left(a\right):=Q_0+\frac{\mathit{r\vartheta }(R_0-Q_0)}{\lambda }\left[\frac{1}{\log a}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}-1\right)-\frac{1-a}{2a\log a}\right].$$ (48)

For p₀ ≈ 0 we have Q°(a) ≈ A(a).

The proof can be found in Appendix A.1.

In accordance to out previous notation we set

$$\overline{A}:=A(\overline{\mathrm{\Lambda }})\mathrm{and}\stackrel{\sim }{A}:=A(\stackrel{\sim }{\mathrm{\Lambda }}).$$ (49)

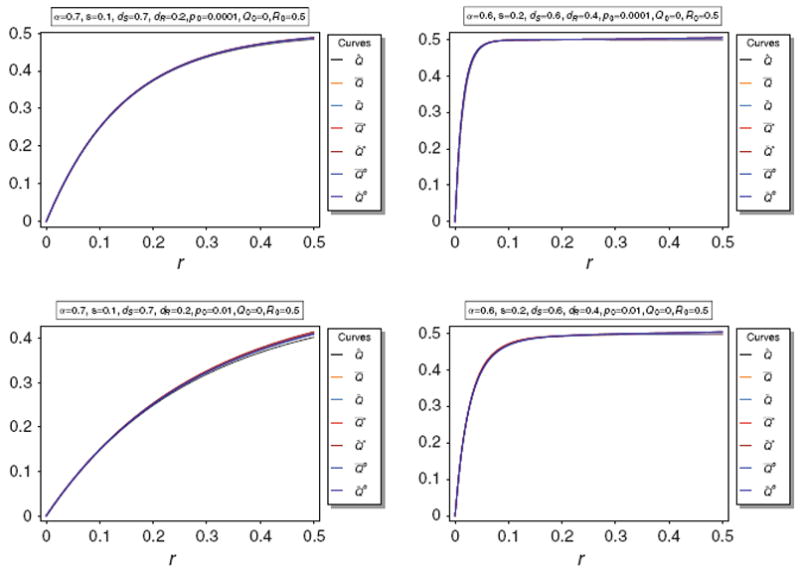
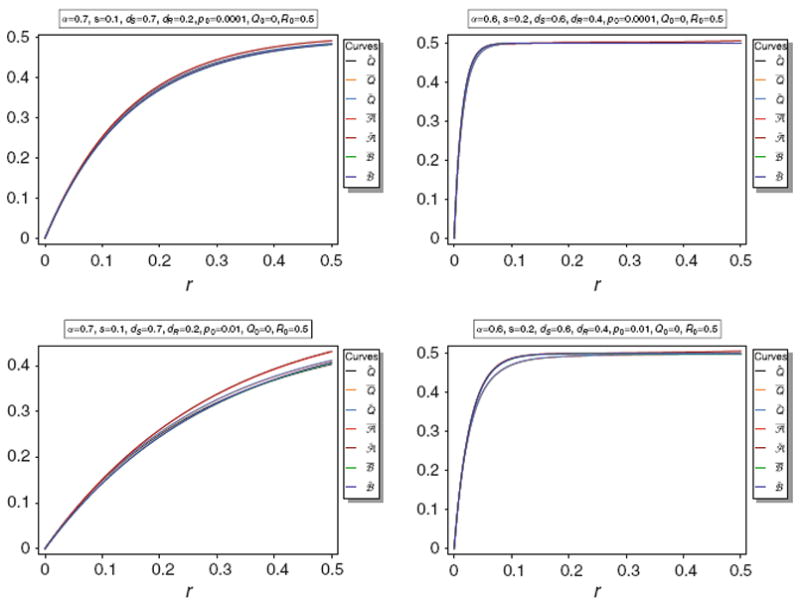
These approximations are illustrated in Fig. 5.

Fig. 5.

Equilibrium frequency Q̂ of the neutral allele N₁ and various bounds of Q̂ as a function of r for different parameter combinations. The panels show Q̂ along with its upper bounds Q̅ and Q̃, as well as the approximations A̅, Ã, B̅, B̃. The parameters are the same as in Fig. 3

Now, we shall additionally assume that a ≈ 1.

Theorem 4

Let a(x) = 1 − rx with $x\in [\frac{\vartheta }{\lambda },\frac{\vartheta }{\mu }]$ and

$$B\left(x\right):=Q_0+\frac{\vartheta \left(R_0-Q_0\right)}{\mathit{x\lambda }}\left(1-p_0^{\frac{\mathit{rx}}{\log \lambda -\log \mu }}\right).$$ (50)

For p₀ ≈ 0 and rx ≈ 0 we have Q°(a(x)) ≈ B(x).

Proof

We have log a(x) ≈ −rx. Hence,

$$\begin{array}{c}{Q}^{\circ }(a(x))\approx Q_0+\frac{\mathit{r\vartheta }(R_0-Q_0)}{\lambda }\left[\frac{1}{-\mathit{rx}}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\mathit{rx}}{\log \lambda -\log \mu }}-1\right)+\frac{\mathit{rx}}{2\left(1-\mathit{rx}\right)\mathit{rx}}\right]\\ =Q_0+\frac{\vartheta \left(R_0-Q_0\right)}{\mathit{x\lambda }}\left[1-{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\mathit{rx}}{\log \lambda -\log \mu }}+\frac{\mathit{rx}}{2\left(1-\mathit{rx}\right)}\right].\end{array}$$

If rx ≈ 0, we can neglect $\frac{\mathit{rx}}{2(1-\mathit{rx})}$ and obtain

$$Q^{\circ }(a(x))\approx Q_0+\frac{\vartheta (R_0-Q_0)}{\mathit{x\lambda }}\left(1-{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\mathit{rx}}{\log \lambda -\log \mu }}\right).$$

Moreover, because p₀ ≈ 0 we have $\frac{p_0}{1-p_0}\approx p_0$. Thus,

$$Q^{\circ }(a(x))\approx Q_0+\frac{\vartheta (R_0-Q_0)}{\mathit{x\lambda }}\left(1-p_0^{\frac{\mathit{rx}}{\log \lambda -\log \mu }}\right).$$

Note that we have $a(\frac{\vartheta (p_0\lambda +(1-p_0)\mu )}{\mathit{\lambda \mu }})=\overline{\mathrm{\Lambda }}$ and $a(\frac{\vartheta }{\lambda })=\stackrel{\sim }{\mathrm{\Lambda }}$. Let us define

$$\overline{B}:=B\left(\frac{\vartheta (p_0\lambda +(1-p_0)\mu )}{\mathit{\lambda \mu }}\right)\mathrm{and}\stackrel{\sim }{B}:=B\left(\frac{\vartheta }{\lambda }\right).$$ (51)

We obtain the following corollary.

Corollary 4

We have

$$\stackrel{\sim }{B}=R_0-(R_0-Q_0)p_0^{\frac{\mathit{r\vartheta }}{\lambda \left(\log \lambda -\log \mu \right)}}.$$ (52)

For p₀ ≈ 0 and $\frac{\mathit{r\vartheta }}{\lambda }\approx 0$, we have Q̃° ≈ B̃.

Figure 5 illustrates the approximations A̅, Ã, B̅, B̃. It is easily seen that the approximations are very accurate unless p₀ is too large (p₀ ≳ 0.1). Anyway, the approximations are still acceptably accurate for p₀ = 0.1.

By expanding $p_0^x$ into a Taylor series around x = 0, and by setting $x=\frac{\mathit{r\vartheta }}{\lambda (\log \lambda -\log \mu )}$ we obtain

$$\stackrel{\sim }{B}=R_0-\left(R_0-Q_0\right)\sum _{k=0}^{\infty }\frac{r^k}{k!}{\left(\frac{\vartheta }{\lambda \left(\log \lambda -\log \mu \right)}\right)}^k\log p_0.$$ (53)

Hence, for r ≈ 0 we can further approximate this by neglecting terms of order O(r²) or O(r³) and higher, and obtain

$$\stackrel{\sim }{C}=Q_0-\left(R_0-Q_0\right)\frac{\mathit{r\vartheta }\log p_0}{\lambda \left(\log \lambda -\log \mu \right)}$$ (54)

and

$$\stackrel{\sim }{D}=Q_0-(R_0-Q_0)\frac{\mathit{r\vartheta }\log p_0}{\lambda \left(\log \lambda -\log \mu \right)}-(R_0-Q_0)\frac{r^2}{2}{\left(\frac{\vartheta }{\lambda \left(\log \lambda -\log \mu \right)}\right)}^2\log p_0.$$ (55)

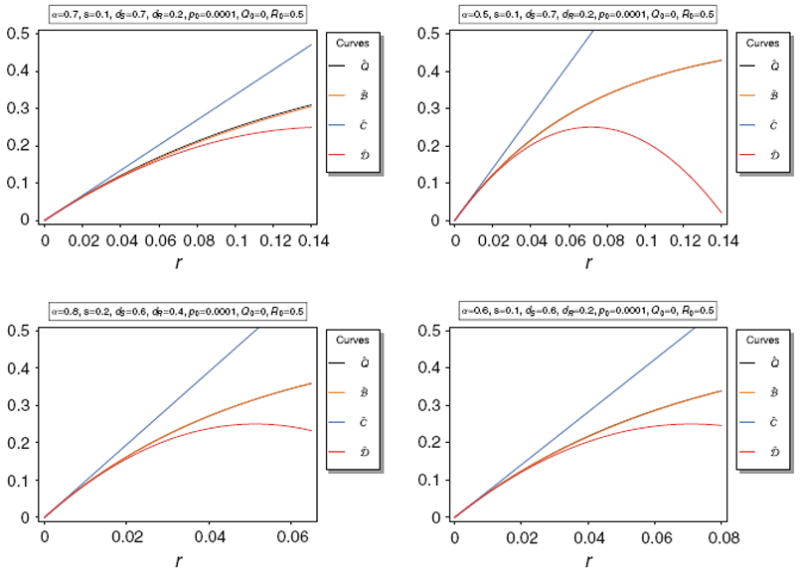
Figure 6 shows Q̂ along with its approximations C̃ and D̃. It is obvious that these approximations are only accurate for very small r. Not surprisingly D̃ is a much better approximation than the linear approximation C̃.

Fig. 6.

Equilibrium frequency Q̂ of the neutral allele N₁ and various bounds of Q̂ as a function of r for various parameter combinations. The panels show Q̂ along with its upper bounds Q̅ and Q̃, as well as the approximations C̃ and D̃.

3.3 The hitchhiking effect for general m

Since the sensitive allele goes extinct in the population, the equilibrium frequency of the neutral allele N₁ is given by (7), i.e., by

$${\widehat{Q}}^{\left(m\right)}=Q_0+\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }\frac{{\vartheta }_{p_{\tau },m}}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l}.$$

The above formula has the same structure as in the case m = 2. If we set m = 1 there is no recombination and hence the initial proportions of the neutral allele among genotypes with the resistant allele remain constant over time. Hence, we have ${\widehat{Q}}^{(1)}=Q_0^{(1)}$.

We shall now derive approximations for Q̂^(m). As easily seen from (7), we can apply our approximations from the case m = 2 if we make the approximation ${\prod }_{l=0}^{\tau -1}{\mathrm{\Lambda }}_{m,l}\approx a^{\tau }$ and ϑ_pτ,m ≈ b. We first approximate ϑ_pτ,m by a constant. From (5b) we obtain

$${\vartheta }_{p_{\tau },m}=\sum _{k=0}^{m-2}\left(\underset{k}{m-2}\right)p_{\tau }^k{\left(1-p_{\tau }\right)}^{m-2-k}\times \left(\frac{\alpha \left(m-1\right)W_1^{(T)}{W}_3^{(T)}}{\left(m-k-1\right)W_1^{(T)}+\left(k+1\right)W_3^{(T)}}+\frac{\left(1-\alpha \right)\left(m-1\right)W_1^{(U)}{W}_3^{(U)}}{\left(m-k-1\right)W_1^{(U)}+\left(k+1\right)W_3^{(U)}}\right).$$

Let

$${\overline{\vartheta }}^{(m)}:=\underset{k=0,\mathrm{\dots },m-2}{\max }\left\{\frac{\alpha \left(m-1\right)W_1^{(T)}{W}_3^{(T)}}{\left(m-k-1\right)W_1^{(T)}+\left(k+1\right)W_3^{(T)}}+\frac{\left(1-\alpha \right)\left(m-1\right)W_1^{(U)}{W}_3^{(U)}}{\left(m-k-1\right)W_1^{(U)}+\left(k+1\right)W_3^{(U)}}\right\}$$ (56)

and

$${\underset{¯}{\vartheta }}^{(m)}:=\underset{k=0,\mathrm{\dots },m-2}{\min }\left\{\frac{\alpha \left(m-1\right)W_1^{(T)}{W}_3^{(T)}}{\left(m-k-1\right)W_1^{(T)}+\left(k+1\right)W_3^{(T)}}+\frac{\left(1-\alpha \right)\left(m-1\right)W_1^{(U)}{W}_3^{(U)}}{\left(m-k-1\right)W_1^{(U)}+\left(k+1\right)W_3^{(U)}}\right\}.$$ (57)

Hence, we have

$${\vartheta }_{p_{\tau },m}\le {\overline{\vartheta }}^{(m)}\sum _{k=0}^{m-2}\left(\underset{k}{m-2}\right)p_{\tau }^k{\left(1-p_{\tau }\right)}^{m-2-k}={\overline{\vartheta }}^{(m)},$$

where the last equality follows from the binomial formula. Similarly, we obtain ϑ_pτ,m ≥ ϑ̲^(m).

Therefore, we obtain

$$1-r\frac{{\overline{\vartheta }}^{\left(m\right)}}{\mathit{\lambda \mu }}\left(\frac{p_0{\lambda }^{t+1}+\left(1-p_0\right){\mu }^{t+1}}{p_0{\lambda }^t+\left(1-p_0\right){\mu }^t}\right)\le {\mathrm{\Lambda }}_{m,t}\le 1-r\frac{{\underset{¯}{\vartheta }}^{\left(m\right)}}{\mathit{\lambda \mu }}\left(\frac{p_0{\lambda }^{t+1}+\left(1-p_0\right){\mu }^{t+1}}{p_0{\lambda }^t+\left(1-p_0\right){\mu }^t}\right).$$

Using the same approximation as in the case m = 2 yields

$${\underset{¯}{\mathrm{\Lambda }}}^{(m)}:=1-r\frac{{\overline{\vartheta }}^{(m)}}{\mu }\le {\mathrm{\Lambda }}_{m,t}\le 1-r\frac{{\underset{¯}{\vartheta }}^{(m)}}{\lambda \mu }(p_0\lambda +(1-p_0)\mu )=:{\overline{\mathrm{\Lambda }}}^{(m)}.$$

Hence, by replacing ϑ and a by ϑ̅^(m) and Λ̅^(m), or ϑ̲^(m) and Λ̲^(m), respectively, we obtain the upper and lower bounds

$${\overline{Q}}^{(m)}=Q_0+\frac{r{\overline{\vartheta }}^{(m)}(R_0-Q_0)}{\lambda }\sum _{k=0}^{\infty }\frac{{\overline{\mathrm{\Lambda }}}^{{(m)}^k}}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^k+1}$$

and

$${\underset{¯}{Q}}^{(m)}=Q_0+\frac{r{\underset{¯}{\vartheta }}^{(m)}(R_0-Q_0)}{\lambda }\sum _{k=0}^{\infty }\frac{{\underset{¯}{\mathrm{\Lambda }}}^{{(m)}^k}}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^k+1},$$

respectively.

It turns out that the upper and lower bounds are very inaccurate estimates for Q̂^(m). However, it is possible to find relative accurate approximations for Q̂^(m), at least if p₀ is small, which is the most important case for our current purpose. If p₀ ≈ 0, we have $\frac{p_0}{1-p_0}\approx 0$, so that we obtain

$$\begin{array}{lll}{\vartheta }_{p_{\tau },m}& \approx & \sum _{k=0}^{m-2}\left(\underset{k}{m-2}\right){\left(\frac{p_0}{1-p_0}\right)}^k{\left(\frac{\lambda }{\mu }\right)}^{t(k)}\\ & & \times \left(\frac{\alpha \left(m-1\right)W_1^{\left(T\right)}{W}_3^{\left(T\right)}}{\left(m-k-1\right)W_1^{\left(T\right)}+\left(k+1\right)W_3^{\left(T\right)}}+\frac{\left(1-\alpha \right)\left(m-1\right)W_1^{\left(U\right)}{W}_3^{\left(U\right)}}{\left(m-k-1\right)W_1^{\left(U\right)}+\left(k+1\right)W_3^{\left(U\right)}}\right)\\ & \approx & \frac{\alpha \left(m-1\right)W_1^{\left(T\right)}{W}_3^{\left(T\right)}}{\left(m-1\right)W_1^{\left(T\right)}+W_3^{\left(T\right)}}+\frac{\left(1-\alpha \right)\left(m-1\right)W_1^{\left(U\right)}{W}_3^{\left(U\right)}}{\left(m-1\right)W_1^{\left(U\right)}+W_3^{\left(U\right)}}=:{\stackrel{\sim }{\vartheta }}^{\left(m\right)}.\end{array}$$ (58)

From (5c) we see that ϑ̃^(m) = θ_0,m Moreover, define

$${\stackrel{\sim }{\mathrm{\Lambda }}}^{(m)}:=1-\frac{r{\stackrel{\sim }{\vartheta }}^{(m)}}{\lambda }.$$ (59)

Hence, by approximating ϑ_pτ,m by ϑ̃^(m) and Λ_m,l by Λ̃^(m) we obtain

$${\widehat{Q}}^{(m)}\approx {\stackrel{\sim }{Q}}^{(m)}=Q_0+\frac{r{\stackrel{\sim }{\vartheta }}^{(m)}(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }\frac{{({\stackrel{\sim }{\mathrm{\Lambda }}}^{(m)})}^{\tau }}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}.$$ (60)

This approximation turns out to be sufficiently accurate unless p₀ is too large.

Clearly, Q̃^(m) can be further approximated as in the case m = 2. However, note that for m > 2 the assumption that p₀ is small is always implicitly made because otherwise the approximation (58) for ϑ_pτ,m will be inaccurate. Hence, only those approximations that were derived under the assumption of p₀ ≈ 0 are meaningful if m > 2, i.e., those of Result 4 and Corollary 4. We can therefore summarize:

Result 2

Let m ≥ 2 and

$${\stackrel{\sim }{B}}^{(m)}:=R_0-(R_0-Q_0)p_0^{\frac{r{\stackrel{\sim }{\vartheta }}^{(m)}}{\lambda (\log \lambda -\log \mu )}}.$$ (61)

Then we have Q̂^(m) ≈ B̃^(m).

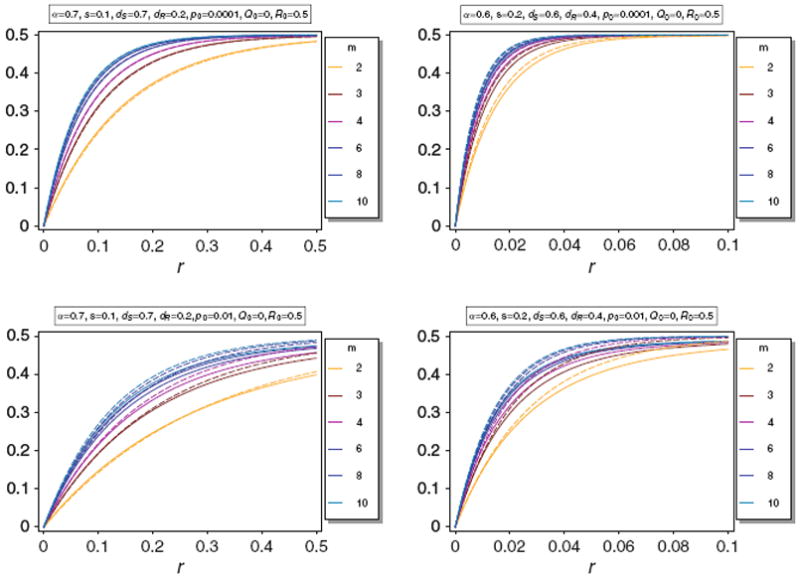
Note, that the approximations become worse for large m. However, as noted in Schneider and Kim (2010), the differences in Q̂^(m) for different values of m become small for large m. Since, in reality m should be bounded by a maximum possible value it should be sufficient to assume m < 10. For these values Result 2 is still accurate. This is illustrated in Fig. 7. Furthermore, note that Result 2 becomes delicate for large m, because it is based on the approximation (58), which becomes very inaccurate as m → ∞.

Fig. 7.

Equilibrium frequency Q̂ ^(m) (thin lines) of the neutral allele N₁ versus the approximation B^(m) (thick dashed lines) for various values of m. The parameters are as in Fig. 3

4 The general model

Schneider and Kim (2010) also presented two generalizations of their model. First, they argued that the differentiation into treated and untreated hosts is oversimplified, and that host heterogeneity should be taken into account. Host heterogeneity can reflect for instance different levels of drug concentration, drug decay, different levels of host-acquired immunity, different immune responses etc. Second, they argued that it is oversimplified to assume that each host is infected by the same number of parasites, i.e., that m is a fixed parameter, and showed how the model can be generalized to the case in which m follows a given frequency distribution.

We shall briefly summarize the two generalizations, and show how our results are generalized.

4.1 Host heterogeneity

Assume again a fixed proportion α of hosts is treated. We divide the treated and untreated host into various different discrete “treated classes” and “untreated classes”. Let the proportion of infected hosts that fall into class j (j ∈ ℕ) be α_j. Let U ⊆ ℕ and T = ℕ\U be the sets of treated and untreated classes, respectively. Hence, we have ${\sum }_{j\in \mathrm{U}}{\alpha }_j=1-\alpha$ and ${\sum }_{j\in \mathrm{T}}{\alpha }_j=\alpha$. Let us denote the fitnesses of parasite haplotypes carrying the sensitive and resistant allele in hosts that fall into class j by $W_1^{\left(j\right)}$ and $W_2^{\left(j\right)}$, and $W_3^{\left(j\right)}$ and $W_4^{\left(j\right)}$, respectively.

Note that in the original formulation of the model we have $W_k^{\left(U\right)}={\sum }_{j\in \mathrm{U}}\frac{{\alpha }_j}{1-\alpha }{W}_k^{\left(j\right)}=\mathrm{E}[W_k^{\left(j\right)}\mid U]$, and $W_k^{\left(T\right)}={\sum }_{j\in \mathrm{T}}\frac{{\alpha }_j}{\alpha }{W}_k^{\left(j\right)}=\mathrm{E}[W_k^{\left(j\right)}\mid T]$. Hence, it can be regarded as the approximation that all untreated hosts are subsumed in just one class, in which $W_k^{\left(U\right)}$ is the mean fitness of the parasites among them and all treated hosts are subsumed in just one class, in which $W_k^{\left(T\right)}$ is the mean fitness of the parasites among them.

In the model accounting for host heterogeneity the equilibrium frequency of the neutral allele N₁ is still given by (7), however the parameters λ, μ, are given by

$$\lambda =\sum _{j=0}^{\infty }{\alpha }_j{W}_3^{\left(j\right)}=\mathrm{E}\left[W_3^{\left(j\right)}\right]=\left(1-\alpha \right)\mathrm{E}\left[W_3^{\left(j\right)}\mid \mathrm{U}\right]+\alpha \mathrm{E}\left[W_3^{\left(j\right)}\mid \mathrm{T}\right]$$ (62a)

and

$$\mu =\sum _{j=0}^{\infty }{\alpha }_j{W}_1^{\left(j\right)}=\mathrm{E}\left[W_1^{\left(j\right)}\right]=\left(1-\alpha \right)\mathrm{E}\left[W_1^{\left(j\right)}\mid \mathrm{U}\right]+\alpha \mathrm{E}\left[W_1^{\left(j\right)}|\mathrm{T}\right],$$ (62b)

whereas ϑ_p,m and Λ_m,t are still given by (5b) and (8), however in (5b) θ_k,m has to be replaced by

$${\theta }_{k,m}=\left(m-1\right)\sum _{j=0}^{\infty }\frac{{\alpha }_j{W}_1^{\left(j\right)}{W}_3^{\left(j\right)}}{\left(m-1-k\right)W_1^{\left(j\right)}+\left(k+1\right)W_3^{\left(j\right)}}.$$ (63)

Hence, in all approximations ϑ̃^(m) has to be replaced by

$${\stackrel{\sim }{\vartheta }}^{\left(m\right)}=\sum _{j=0}^{\infty }\frac{{\alpha }_j\left(m-1\right)W_1^{\left(j\right)}{W}_3^{\left(j\right)}}{\left(m-1\right)W_1^{\left(j\right)}+W_3^{\left(j\right)}}.$$ (64)

We summarize:

Result 3

Let m ≥ 2. The equilibrium frequency of the neutral allele N₁, Q̂^(m), is approximately given by

$${\stackrel{\sim }{B}}^{(m)}:=R_0-(R_0-Q_0)p_0^{\frac{r{\stackrel{\sim }{\vartheta }}^{(m)}}{\lambda (\log \lambda -\log \mu )}},$$ (65)

where λ,μ, and ϑ̃^(m) are given by (62a), (62b), and (64), respectively.

It was mentioned in Schneider and Kim (2010) that accounting for host heterogeneity results in a more pronounced hitchhiking compared to the basic model if the values of λ and μ coincide, or more precisely if $W_k^{(U)}=\mathrm{E}[W_k^{\left(j\right)}\mid \mathrm{U}]$, and $W_k^{(T)}=\mathrm{E}[W_k^{\left(j\right)}\mid \mathrm{T}]$. The reason is that under this assumption ϑ̃^(m) given by (64) is smaller than if it is given by (58), and (for fixed m) the respective approximations for the hitchhiking effect corresponds to standard hitchhiking with recombination rate $\frac{{\stackrel{\sim }{\vartheta }}^{(m)}r}{\lambda }$ and initial frequency $\frac{\mu p_0}{\lambda (1-p_0)+\mu p_0}$. We will prove this in the Sect. 5.

4.2 Number of co-infections

Now, assume that the number m of parasites that infect a host follows some probability distribution over the population. Let κ_m denote the probability that a host is infected by m ≥ 1 parasites. Naturally, we have ${\sum }_{m=1}^{\infty }{\kappa }_m=1$.

As shown in Schneider and Kim (2010), the equilibrium frequency of the neutral allele N₁ is given by

$${\widehat{Q}}^{(\kappa )}=Q_0+\frac{r(R_0-Q_0)}{\lambda }\sum _{\tau =0}^{\infty }\frac{{\vartheta }_{p_{\tau },\kappa }}{\frac{p_0}{1-p_0}{\left(\frac{\lambda }{\mu }\right)}^{\tau }+1}\prod _{l=0}^{\tau -1}{\mathrm{\Lambda }}_{\kappa ,l},$$ (66a)

with

$${\vartheta }_{p_{\tau },\kappa }=\sum _{m=1}^{\infty }{\kappa }_m{\vartheta }_{p_{\tau },m}\mathrm{and}{\mathrm{\Lambda }}_{\kappa ,t}=\sum _{m=1}^{\infty }{\kappa }_m{\mathrm{\Lambda }}_{m,t},$$ (67a)

where ϑ_pτ,m and Λ_m,t are given by (5b) and (8) (eventually with λ, μ, ϑ_p,m, Λ_m,t, and θ_k,m adjusted as in Sect. 4.1 to incorporate host heterogeneity). Hence, the equilibrium frequency of the neutral allele N₁ can be approximated following the calculations of Sect. 3. We can summarize this in the following result.

Result 4

The equilibrium frequency of the neutral allele N₁, Q̂^(κ) is approximately given by

$${\stackrel{\sim }{Q}}^{(\kappa )}\approx {\stackrel{\sim }{B}}^{(\kappa )}:=R_0-(R_0-Q_0)p_0^{\frac{r{\stackrel{\sim }{\vartheta }}^{(\kappa )}}{\lambda (\log \lambda -\log \mu )}}$$ (68)

with ${\stackrel{\sim }{\vartheta }}_{\kappa }={\sum }_{m=1}^{\infty }{\kappa }_m{\stackrel{\sim }{\vartheta }}_m$, where λ, μ, and ϑ̃^(m) are given by (4), and (58), respectively. If one wants to incorporate host heterogeneity, λ, μ, and ϑ̃^(m) are given by (62), and (64), respectively.

5 Equilibrium heterozygosity and the hitchhiking effect

From now on we assume that m follows a probability distribution as in Sect. 4.2 and we account for host heterogeneity as in Sect. 4.1 unless otherwise mentioned.

Remember that the equilibrium heterozygozity is given by

$$\widehat{H}=2{\widehat{Q}}^{(\kappa )}(1-{\widehat{Q}}^{(\kappa )}).$$ (69)

We have seen in the last section that the equilibrium frequency, and its upper and lower bounds and approximations are given by expressions of the form Q₀ + (R₀ − Q₀) A(r), where A is a function of the recombination rate that has to be chosen appropriately. For brevity we will suppress the dependence of Q̂^(κ) on r unless necessary. Let us regard R₀, i.e., the initial frequency of N₁ among sensitive parasites, as a random variable and the heterozygosity as a function of R₀. Let us write

$$\widehat{H}=\widehat{H}(R_0)=2(Q_0+(R_0-Q_0)A(r))(1-Q_0-(R_0-Q_0)A(r)).$$ (70)

Given the initial frequency of the neutral allele N₁ is R₀, the beneficial mutation occurs initially in association with allele N₁ with probability R₀, and in association with allele N₂ with probability (1 − R₀). Hence, we have Q₀ = 1 with probability R₀ and Q₀ = 0 with probability (1 − R₀). Therefore, the average heterozygosity given R₀ is calculated to be

$$\begin{array}{lll}\mathrm{E}(\widehat{H}\mid R_0)& =& 2R_0(1+(R_0-1)A(r))(Q_0-R_0)A(r)+2(1-R_0)R_{0}A(r)(1-R_{0}A(r))\\ & =& (R_0-R_0^2)(2A(r)-A^2(r)).\end{array}$$ (71)

Hence, according to the theorem of total probability, the average heterozygosity is calculated to be

$$\mathrm{E}(\widehat{H})=\mathrm{E}\left(\mathrm{E}\left(\widehat{H}\mid R_0\right)\right)=2\left(\mathrm{E}(R_0)-\mathrm{E}\left(R_0^2\right)\right)(2A(r)-A^2(r)).$$ (72)

The initial heterozygosity is given by H₀ = 2R₀(1 − R₀). Hence, the fraction of the expected equilibrium heterozygosity over the initial heterozygosity is given by

$$H(r)=\frac{\mathrm{E}(\widehat{H})}{\mathrm{E}(H_0)}=2A(r)-A^2(r),$$ (73)

which is independent of the distribution of R₀. Since A(0) = 0 we have H(0) = 0.

If we further approximate Q̂ by B̃ given by (52), we obtain

$$H^{(\kappa )}(r)\approx {\stackrel{\sim }{H}}^{(\kappa )}=1-p_0^{\frac{2r{\stackrel{\sim }{\vartheta }}^{(\kappa )}}{\lambda (\log \lambda -\log \mu )}}.$$ (74)

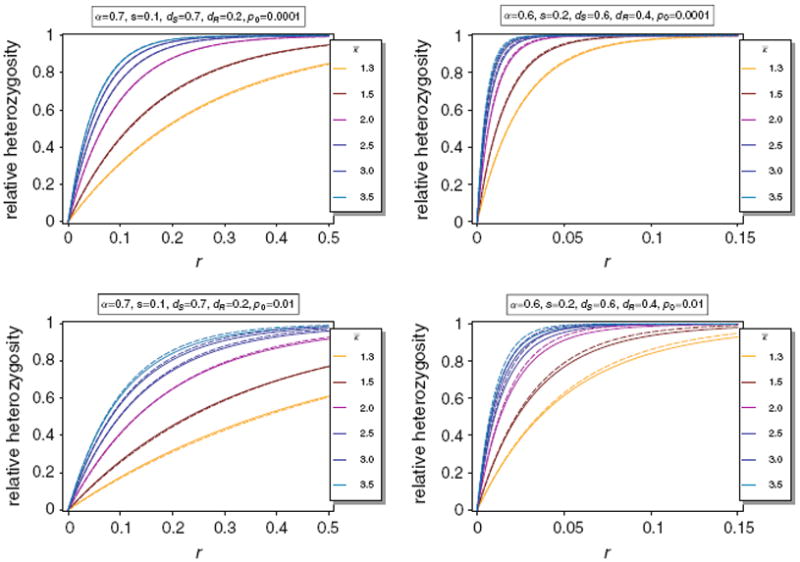
From (74) it is seen that H^(κ) shows a strong genome-wide reduction if κ₁ is large and selection is sufficiently strong. The approximation is illustrated in Fig. 8.

Fig. 8.

Relative expected heterozygosity H^(κ) (thin lines) of the neutral allele N₁ versus the approximation H̃^(κ) (thick dashed lines) for different distributions κ. In all cases we assume a truncated exponential distribution with range 1–10 and mean κ̅. By truncated we mean that the probability of m = 10 is the probability that m ≥ 10 for a poisson distribution with mean κ̅. The parameters are as in Fig. 3

For the special case that m is constant the above reduces to $H^{(m)}(r)\approx {\stackrel{\sim }{H}}^{(m)}=1-p_0^{\frac{2r{\stackrel{\sim }{\vartheta }}^{(m)}}{\lambda (\log \lambda -\log \mu )}}$ which is increasing as a function of m. The reason is that ϑ̃^(m) is monotone increasing in m, either if it is given by (58) or in the case of host heterogeneity by (64).

It was mentioned in Schneider and Kim (2010) that accounting for host heterogeneity results in a more pronounced hitchhiking compared to the basic model if the values of λ and μ coincide, or, more precisely, if $W_k^{(U)}=\mathrm{E}[W_k^{\left(j\right)}\mid \mathrm{U}]$ and $W_k^{(T)}=\mathrm{E}[W_k^{\left(j\right)}\mid \mathrm{T}]$. The reason is that, for every m, under these assumptions ϑ̃^(m) given by (64) is smaller than if it is given by (58). Hence, this holds also for the corresponding values of ϑ̃^(κ), and consequently (74) is smaller if host heterogeneity is incorporated. We shall summarize this as a remark and prove it in the appendix.

Remark 4

Host heterogeneity leads to an increased hitchhiking effect, i.e., to a stronger reduction in relative heterozygosity H̃^(κ)(r), compared to the basic model with only one class of treated and one class of untreated hosts with corresponding fitness parameters, i.e., $W_k^{(U)}=\mathrm{E}[W_k^{\left(j\right)}\mid \mathrm{U}]$, and $W_k^{(T)}=\mathrm{E}[W_k^{\left(j\right)}\mid \mathrm{T}]$.

For fixed large m the differences in H̃^(m) become very small and vanish in the limit m → ∞ because H̃^(m) approaches the classical approximation for standard hitchhiking.

Note, that the last statement of the remark is delicate, because the approximation H̃^(m) will be inaccurate for very large m.

We can use (73), or (74) to calculate the maximum recombination distance for which a given reduction in relative heterozygosity can be observed. This is relevant for predicting the width of the valley of relative heterozygosity for given selection parameters. By comparison of (73), or (74) with empirical data on the relative heterozygosity, it is possible to re-evaluate or validate parameter estimates (e.g., for α, λ, μ, etc.).

From (73) we obtain that the maximum recombination rate, r̂, for which the relative heterozygosity is smaller than β by solving the equation H(r̂) = β. If we solve this equation first with respect to A(r̂), we obtain

$$A(\widehat{r})=1-\sqrt{1-{\beta }^2}.$$ (75)

By using the approximation according to (74), we obtain

$$\widehat{r}=\frac{\lambda \log (1-{\beta }^2)(\log \lambda -\log \mu )}{2{\stackrel{\sim }{\vartheta }}^{(\kappa )}\log p_0}.$$ (76)

Figure 9 illustrates the valley of reduced heterozygosity as a function of α for different distributions κ of m. Such illustrations can be used to determine the range of parameters that lead to a given reduction in relative heterozygosity.

Fig. 9.

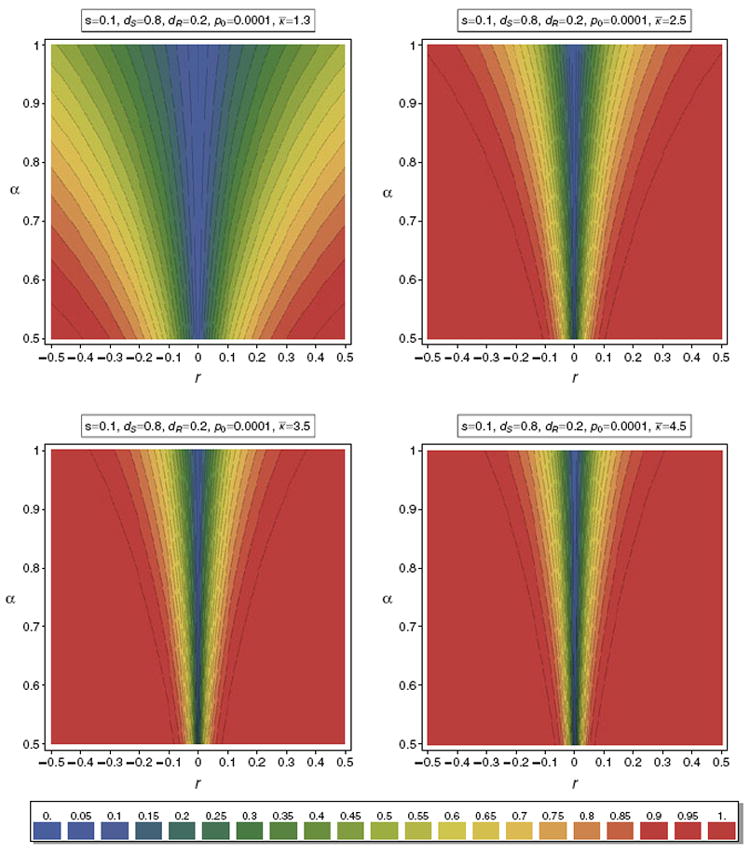
Contour plot of the valley of reduced heterozygosity for different distributions κ. In all cases we assume a truncated exponential distribution with range 1–10 and mean κ̅. By truncated we mean that the probability of m = 10 is the probability that m ≥ 10 for a poisson distribution with mean κ̅. In all panels the same selection parameters are assumed. The parameters are summarized in the boxes above the panels

6 Discussion

We obtained a closed-form approximation for the expected heterozygosity shaped by genetic hitchhiking in the model of antimalarial drug-resistance evolution proposed in Schneider and Kim (2010). This model aims to capture the effect of multiple infections per host (m) and drug-treatment rate (α), which are considered the most important epidemiological parameters that characterize geographic differences in the dynamics of drug resistance (Escalante et al. 2009), as well as the complex malaria transmission cycle on the pattern of selective sweeps caused by drug-resistant mutations (Daily 2006; Prugnolle et al. 2009). Due to the model complexity the exact solution is expressed by the summation of infinite (or a very large number of) terms. Here, we provided numerous approximate solutions with varying degree of accuracy. Notably, using the assumption that the starting frequency of the resistant allele under positive directional selection is low, we could obtain a solution that is simple enough to allow clear biological interpretations regarding the effects of epidemiological parameters. Furthermore, our approximations are flexible enough to incorporate arbitrary distributions of hosts with different infection rates and/or host heterogeneity, e.g., arbitrary distributions of hosts with different drug concentrations. The latter condition, arising due to a slow decay of antimalarial drugs in the bodies of treated patients, was demonstrated to be crucial for the initiation of drug resistance evolution (Hastings et al. 2002). For more discussion on how this model can be used to predict the spread of resistance and its speed, and how it can be used to design ‘optimal’ treatment strategies we refer to Schneider and Kim (2010).

The mean fitness of the resistant parasites, λ, and of the sensitive parasites, μ, are crucial in the considered model. If λ and μ are not too different, log λ − log μ corresponds to the selection coefficient of the beneficial (resistant) mutation. Then, our approximation (74) is basically identical to that under the standard model of hitchhiking obtained by Maynard Smith and Haigh (1974) except the modifying factors of the recombination rate, $\frac{{\stackrel{\sim }{\vartheta }}^{\left(\kappa \right)}}{\lambda }$, and of the initial frequency, $\frac{\mu }{\lambda \left(1-p_0\right)+\mu p_0}$. Therefore, the dynamics of hitchhiking unique to this malaria model is summarized by these factors. We have $\frac{{\stackrel{\sim }{\vartheta }}^{\left(\kappa \right)}}{\lambda }<1$ because $\frac{\left(m-1\right)W_1^{\left(j\right)}}{\left(m-1\right)W_1^{\left(j\right)}+W_3^{\left(j\right)}}<1$ for all host class j and all m. The latter fraction represents the probability that a given resistant gametocyte pairs with a sensitive gametocyte in the body of a mosquito which took its blood meal from a j host, when the frequency of resistant allele is low. (As with the standard hitchhiking model, the final heterozygosity is predominantly determined by the dynamics of the resistant allele at its early stage.) If the drug in the host is very effective ( $W_1^{\left(j\right)}\ll W_3^{\left(j\right)}$), it will greatly reduce $\frac{{\stackrel{\sim }{\vartheta }}^{\left(\kappa \right)}}{\lambda }$. Namely, the strength of selection determines the effective rate of recombination (decay of association between beneficial and neutral allele), unlike the case of standard hitchhiking model in which the two factors are decoupled. Moreover, the approximation (74) will be more accurate even for larger r and p₀ compared to the standard hitchhiking model because of the two adjustment factors $\frac{{\stackrel{\sim }{\vartheta }}^{(\kappa )}}{\lambda }$ and $\frac{\mu }{\lambda (1-p_0)+\mu p_0}$.

Assume m is constant. It is also obvious from the above that the number, m, of independent parasite strains infecting a host determines the effective recombination rate. A small value of m thus increases the hitchhiking effect. In the extreme case of m = 1, genetic variation in the population is completely wiped out as parasites reproduce effectively asexually. On the other hand, with m → ∞ our approximation approaches that of standard hitchhiking. Note, however, that in the exact solution $\frac{{\vartheta }^{\left(m\right)}}{\lambda }$ is still less than one, even with m → ∞, because the approximation leading to ϑ̃^(m) (Eq. 58) assumes that the frequency of the resistant allele is low and hence that the probability that a given host is infected by two or more resistant strains is negligible. However, if m increases to a large number, such chance is no longer negligible. Therefore, the combined effect of strong drug pressure and the limited number of clones in hosts can greatly amplify the effect of genetic hitchhiking beyond the level predicted by the standard model. If m is not constant, the hitchhiking effect is more pronounced for more left-skewed distributions κ. It will be in particular pronounced if a large fraction of single infections occurs.

Our approximation also reveals another important departure of our model from the previous models that assume random mating and homogeneous selective pressures. In the standard model, the allele-frequency trajectory of a beneficial mutation is necessary and sufficient information for predicting its hitchhiking effect on the linked neutral variation (Betancourt et al. 2004; Chevin and Hospital 2008). For example, the speed with which the beneficial mutation increases in the population determines the size of the genomic regions affected by hitchhiking. However, in our model with host heterogeneity, different combinations of parameter values (j and $W_i^{\left(j\right)}$) that specify the same allele frequency trajectory of the resistance allele may generate different hitchhiking effects. Schneider and Kim (2010) showed that the changes of sensitive and resistant allele frequencies are uniquely determined by their absolute fitness, μ and λ, respectively. With host heterogeneity, the fitness is simply the mean of $W_1^{\left(j\right)}$ or $W_3^{\left(j\right)}$ weighted by the frequencies of host classes (α_j). The modifying factor of effective recombination rate, $\frac{{\stackrel{\sim }{\vartheta }}^{\left(m\right)}}{\lambda }$ (ore more generally $\frac{{\stackrel{\sim }{\vartheta }}^{\left(\kappa \right)}}{\lambda }$), however is not a linear function of $W_1^{\left(j\right)}$ or $W_3^{\left(j\right)}$. As a result, as shown in Remark 4, $\frac{{\stackrel{\sim }{\vartheta }}^{\left(m\right)}}{\lambda }$ (or $\frac{{\stackrel{\sim }{\vartheta }}^{\left(\kappa \right)}}{\lambda }$)) decreases as one introduces host heterogeneity while keeping λ and μ constant. This makes our simplest approximation assuming no host heterogeneity a conservative predictor of the hitchhiking effect.

Comparison of approximate solutions with empirical observation of local reductions of genetic variation around the loci of drug resistance mutations, combined with other genetic (e.g. recombination rate, the frequency change of drug resistance) and epidemiological (e.g. the mean number of independent parasite clones per host) information, will greatly advance our understanding of antimalarial drug-resistance evolution. Especially, if empirical data for the reduction in heterozygosity is available, our results can be used to determine possible ranges for parameters that are unknown and/or infeasible to measure. It should be noted that the fraction λ/μ can be easily estimated from retrospective genetic data. Since $\log \frac{p_t}{1-p_t}=t\log \frac{\lambda }{\mu }$, log λ/μ is just the slope of the linear regression of the logarithm of the ratio of resistant over sensitive parasites measured at different time points. However, it is difficult to scale time, because the number of transmission cycles per year is difficult to quantify. Moreover, also the parameter α should be easy to measure. On the opposite, the distribution of κ of m will be difficult to estimate. However, the distribution of m, and especially single infections, lead to a genome-wide reduction in relative heterozygosity if selection is sufficiently strong. This genome-wide reduction might be used to estimate the distribution κ. However, applying our results to real data lies beyond the scope of this article and will be accomplished in a follow-up paper.

Appendix A

A.1 Bounds and approximations

Proof of Remark 2

If $a={\left(\frac{\mu }{\lambda }\right)}^l$ for l ∈ ℕ we just need to adapt the proof of Theorem 1. The derivation of G₁ assumed $\frac{\xi }{\eta }\notin \mathbb{Z}$. If this assumption is violated we have to adjust the derivation. In this case we have $-\frac{\xi }{\eta }=l$ and we can replace (24) by

$$\begin{array}{lll}g(x)& =& \frac{e^{-\mathit{xl\eta }}}{{\mathit{ce}}^{\mathit{x\eta }}+1}=e^{-\mathit{xl\eta }}\sum _{k=0}^{\infty }{(-{\mathit{ce}}^{\mathit{x\eta }})}^k=\sum _{k=0}^{\infty }{(-c)}^k{e}^{\mathit{x\eta }(k-l)}\\ & =& {(-c)}^l\sum _{k=0}^{\infty }{(-c)}^{k-l}{e}^{\mathit{x\eta }(k-l)}.\end{array}$$

Hence, we have to replace (25) in the proof of Theorem 1 by

$$\begin{array}{lll}{G}_1\left(x\right)& =& \mathit{\int }g\left(x\right)\mathrm{d}x=\mathit{\int }{\left(-c\right)}^l\sum _{k=0}^{\infty }{\left(-c\right)}^{k-l}{e}^{\mathit{x\eta }\left(k-l\right)}\mathrm{d}x\\ & =& {\left(-c\right)}^l\sum _{k=0}^{\infty }\mathit{\int }{\left(-c\right)}^{k-l}{e}^{\mathit{x\eta }\left(k-l\right)}\mathrm{d}x\\ & =& {\left(-c\right)}^l\left(\sum _{k=0}^{l-1}\mathit{\int }{\left(-c\right)}^{k-l}{e}^{\mathit{x\eta }\left(k-l\right)}\mathrm{d}x+\mathit{\int }\mathrm{d}x+\sum _{k=l+1}^{\infty }\mathit{\int }{\left(-c\right)}^{k-l}{e}^{\mathit{x\eta }\left(k-l\right)}\mathrm{d}x\right)\\ & =& {\left(-c\right)}^l\left(\sum _{k=0}^{l-1}{\left(-c\right)}^{k-l}\frac{e^{\mathit{x\eta }\left(k-l\right)}}{\eta \left(k-l\right)}+x+\sum _{k=l+1}^{\infty }{\left(-c\right)}^{k-l}\frac{e^{\mathit{x\eta }\left(k-l\right)}}{\eta \left(k-l\right)}\right)\\ & =& {\left(-c\right)}^l\left(\sum _{k=0}^{l-1}{\left(-c\right)}^{k-l}\frac{e^{\mathit{x\eta }\left(k-l\right)}}{\eta \left(k-l\right)}+x-\frac{1}{\eta }\sum _{k=1}^{\infty }{\left(-c\right)}^{k-1}\frac{e^{\mathit{x\eta k}}}{k}\right)\\ & =& {\left(-c\right)}^l\left(\sum _{k=0}^{l-1}{\left(-c\right)}^{k-l}\frac{e^{\mathit{x\eta }\left(k-l\right)}}{\eta \left(k-l\right)}+x-\frac{\log \left(1+{\mathit{ce}}^{\mathit{x\eta }}\right)}{\eta }\right),\end{array}$$

Thus, we have

$$G_1\left(-1\right)={\left(-c\right)}^l\left(\sum _{k=0}^{l-1}\frac{{\left(-c\right)}^{k-l}}{\eta \left(k-l\right)}-1-\frac{\log \left(1+{\mathit{ce}}^{-\eta }\right)}{\eta }\right),$$ (77)

$$G_1\left(0\right)={\left(-c\right)}^l\left(\sum _{k=0}^{l-1}\frac{{\left(-c\right)}^{k-l}}{\eta \left(k-l\right)}-\frac{\log \left(1+c\right)}{\eta }\right),$$ (78)

and

$$G_1\left(x_0\right)={\left(-c\right)}^l\left(\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^{(k-l)}}{\eta \left(k-l\right)}+x_0-\frac{\log 2}{\eta }\right).$$ (79)

Combining the above with (26), the definitions of ξ, η, c, (31), and (32) yields

$$\begin{array}{lll}\psi \left({\left(\frac{\mu }{\lambda }\right)}^l\right)& =& Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda }\\ & & \times [\frac{{\left(\frac{p_0}{1-p_0}\right)}^l}{\log \lambda -\log \mu }\left(\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}\left(1-{\left(\frac{p_0}{1-p_0}\right)}^{k-l}\right)-\log 2p_0\right)\\ & & -\frac{{\left(\frac{p_0}{1-p_0}\right)}^l}{l\left(\log \lambda -\log \mu \right)}\left(1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,l\\ 1+l\end{array}\mid -1\right)\right)],\end{array}$$ (80)

and

$$\begin{array}{lll}\mathrm{\Psi }\left({\left(\frac{\mu }{\lambda }\right)}^l\right)& =& Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda }\\ & & \times [\frac{{\left(\frac{p_0}{1-p_0}\right)}^l}{\log \lambda -\log \mu }\left(\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}{(1-\left(\frac{p_0\mu }{\left(1-p_0\right)\lambda }\right)}^{k-l}\right)\\ & & -\log \left(\frac{p_0\lambda }{p_0\mu +\left(1-p_0\right)\lambda }\right)+\log \lambda +\log \mu -\log 2)\\ & & -\frac{{\left(\frac{p_0}{1-p_0}\right)}^l}{l\left(\log \lambda -\log \mu \right)}\left(1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,l\\ 1+l\end{array}\mid -1\right)\right)],\end{array}$$ (81)

respectively. Note that we have

$$1-{}_2\mathrm{F}_1\left(\begin{array}{c}1,l\\ 1+l\end{array}\mid -1\right)=1-\sum _{k=0}^{\infty }\frac{{\left(1\right)}_{\overline{k}}{\left(l\right)}_{\overline{k}}{\left(-1\right)}^k}{{\left(l+1\right)}_{\overline{k}}k!}=1-\sum _{k=0}^{\infty }\frac{l{\left(-1\right)}^k}{l+k}$$ (82)

$$=1-l{\left(-1\right)}^l\left(\sum _{k=1}^{\infty }\frac{{\left(-1\right)}^k}{k}-\sum _{k=1}^{l-1}\frac{{\left(-1\right)}^k}{k}\right)$$ (83)

$$=\frac{l{\left(-1\right)}^{2l}}{l}-l{\left(-1\right)}^l\left(\log 2-\sum _{k=1}^{l-1}\frac{{\left(-1\right)}^k}{k}\right)$$ (84)

$$=l{\left(-1\right)}^l\left(\sum _{k=1}^l\frac{{\left(-1\right)}^k}{k}-\log 2\right)$$ (85)

$$=l\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}-l{\left(-1\right)}^l\log 2.$$ (86)

Hence, (80) and (81) simplify to

$$\begin{array}{lll}\psi \left({\left(\frac{\mu }{\lambda }\right)}^l\right)& =& Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda }\\ & & \times \left[\frac{{\left(\frac{p_0}{1-p_0}\right)}^l}{\log \mu -\log \lambda }\left({\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}\left(\frac{p_0}{1-p_0}\right)}^{k-l}-\log p_0\right)\right],\end{array}$$ (87)

and

$$\mathrm{\Psi }\left({\left(\frac{\mu }{\lambda }\right)}^l\right)=Q_0+\frac{r\vartheta \left(R_0-Q_0\right)}{\lambda }[\frac{{\left(\frac{p_0}{1-p_0}\right)}^l}{\log \mu -\log \lambda }(\sum _{k=0}^{l-1}\frac{{\left(-1\right)}^k}{k-l}{\left(\frac{p_0\mu }{\left(1-p_0\right)\lambda }\right)}^{k-l}-\log \left(\frac{p_0\mu }{p_0\mu +\left(1-p_0\right)\lambda }\right))],$$ (88)

which equal (36) and (35), respectively.

Now, let us regard g(x) given by (17) as a function in x and a and write g_a(x) for it. Clearly for x ≥ 0, g_a(x) is monotone increasing in a, and for x < 0 it is monotone decreasing. Since by Theorem 1 the integral ${\mathit{\int }}_{\stackrel{\sim }{x}}^{\infty }{g}_a(x)\mathrm{d}x$ exists for x̃ ∈ {−1, 0} and $a\ne {(\frac{\mu }{\lambda })}^l$, it follows by the Theorems of monotone convergence and, in case x̃ = −1, also by the theorem of dominated convergence that ${\lim }_{a\to a_0}{\mathit{\int }}_{\stackrel{\sim }{x}}^{\infty }{g}_a(x)\mathrm{d}x={\mathit{\int }}_{\stackrel{\sim }{x}}^{\infty }{g}_{a_0}(x)\mathrm{d}x$. By setting $a_0={\left(\frac{\mu }{\lambda }\right)}^l$ it follows that (36) and (35) are the continuations of (16) and (15) in the limit $a\to {\left(\frac{\mu }{\lambda }\right)}^l$.

If x₀ ≤ 0, we do not need the function G₁, and hence the derivations from Theorem 1 and Remark 1 hold for ψ. The same holds for Ψ if x₀ ≤ −1. This finishes the proof.

Proof of Theorem 2

For κ ≠ −l(l ∈ ℕ) we have

$${}_2\mathrm{F}_1\left(\begin{array}{c}1,\kappa \\ 1+\kappa \end{array}\mid z\right)=\sum _{k=0}^{\infty }\frac{{\left(\kappa \right)}_{\overline{k}}{z}^k}{{\left(\kappa +1\right)}_{\overline{k}}}=1+\kappa \sum _{k=1}^{\infty }\frac{z^k}{\kappa +k}\approx 1+\frac{\mathit{\kappa z}}{\kappa +1}.$$ (89)

First assume $a\ne {\left(\frac{\mu }{\lambda }\right)}^l$ for l ∈ ℕ, i.e., $\frac{\xi }{\eta }\ne -l$.

Setting $\kappa =\frac{\xi }{\eta }$ and z = −c gives

$${}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -c\right)\approx 1-\frac{\mathit{c\xi }}{\eta +\xi }=1-\frac{p_0\log a}{\left(\log a+\log \lambda -\log \mu \right)\left(1-p_0\right)},$$ (90)

whereas setting $\kappa =\frac{\xi }{\eta }$ and $z=-\frac{c}{\eta }$ gives

$${}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -\frac{c}{e^{\eta }}\right)\approx 1-\frac{\mathit{c\xi }}{e^{\eta }\left(\eta +\xi \right)}=1-\frac{p_0\mu \log a}{\left(\log a+\log \lambda -\log \mu \right)\left(1-p_0\right)\lambda }.$$ (91)

Moreover, setting $\kappa =\frac{-\xi }{\eta }$ and z = −1 yields

$${}_2\mathrm{F}_1\left(\begin{array}{c}1,-\frac{\xi }{\eta }\\ 1-\frac{\xi }{\eta }\end{array}\mid -1\right)\approx 1-\frac{\xi }{\xi -\eta }=1-\frac{\log a}{\log a-\log \lambda +\log \mu },$$ (92)

whereas by setting $\kappa =\frac{\xi }{\eta }$ and z = −1 we obtain

$${}_2\mathrm{F}_1\left(\begin{array}{c}1,\frac{\xi }{\eta }\\ 1+\frac{\xi }{\eta }\end{array}\mid -1\right)\approx 1-\frac{\xi }{\xi +\eta }=1-\frac{\log a}{\log a+\log \lambda -\log \mu }.$$ (93)

First, combining (93), (90), and (92) with (31), and using this approximation in (20) yields (39) by using the definitions of ξ and η. Similarly, we obtain (40) by combining (93), (91), (92), with (32) and (21).

Clearly, (39) and (40) are continuous especially also at $a={\left(\frac{\mu }{\lambda }\right)}^l$. Since ψ(a) and Ψ(a) have continuations at $a={\left(\frac{\mu }{\lambda }\right)}^l$ for (l ∈ ℕ) according to Remark 2, we have ϕ(a) ≈ ψ(a) and Φ(a) ≈ Ψ(a) for all a. This finishes the proof.

Proof of Remark 3

We obtain (41) by combining (33) with (89) for $\kappa =\frac{\log a}{\log \mu -\log \lambda }$ and $z=-\frac{1-p_0}{p_0}$, whereas we obtain (42) by combining (34) with (89) for $\kappa =\frac{\log a}{\log \mu -\log \lambda }$ and $z=-\frac{(1-p_0)\lambda }{p_0\mu }$.

Clearly (39), (40), (41), and (42) are continuous functions in p₀. For $p_0=\frac{1}{2}$ it is easily seen that (39) equals (41), whereas for $p_0=\frac{\lambda }{\lambda +\mu }$ (40) equals (42). Hence, (41) and (42) are the continuations in p₀ of (39) and (40), respectively.

Proof of Theorem 3

Note that we have

$$Q^{\circ }(a)=Q_0+\frac{\mathit{r\vartheta }(R_0-Q_0)}{\lambda }A,$$ (94)

where

$$\begin{array}{lll}A& =& {\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}\left(\frac{1}{\log a}-\frac{1}{\log \frac{a\lambda }{\mu }}+\frac{1}{\log \frac{a\mu }{\lambda }}\right)\\ & & -\frac{1}{2a\log a}+\frac{p_0\mu }{2(1-p_0)\mathit{a\lambda }\log \frac{\mathit{a\lambda }}{\mu }}-\frac{1}{2\log a}+\frac{p_0}{2(1-p_0)\log \frac{\mathit{a\lambda }}{\mu }}\\ & =& {\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}\left(\frac{1}{\log a}+\frac{1}{\log \frac{\mathit{a\mu }}{\lambda }}\right)-\frac{1}{\log a}\left(\frac{1+a}{2a}\right)\\ & & -{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}\left(\frac{1}{\log \frac{\mathit{a\lambda }}{\mu }}\right)+\frac{p_0}{2(1-p_0)\log \frac{\mathit{a\lambda }}{\mu }}\left(\frac{\mu }{\mathit{a\lambda }}+1\right)\\ & =& {\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}\left(\frac{1}{\log a}+\frac{1}{\log \frac{\mathit{a\mu }}{\lambda }}\right)-\frac{1+a}{2a\log a}\\ & & -\frac{p_0}{(1-p_0)\log \frac{\mathit{a\lambda }}{\mu }}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log \frac{a\lambda }{\mu }}{\log \mu -\log \lambda }}-1\right)+\frac{p_0}{2(1-p_0)\log \frac{\mu }{\mathit{a\lambda }}}\left(\frac{\mu }{a\lambda }-1\right)\\ & =& \frac{1}{\log a}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}-1\right)-\frac{p_0}{(1-p_0)\log \frac{\mathit{a\lambda }}{\mu }}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log \frac{a\lambda }{\mu }}{\log \mu -\log \lambda }}-1\right)\\ & & -\frac{1-a}{2a\log a}+\frac{1}{\log \frac{\mathit{a\mu }}{\lambda }}{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}-\frac{p_0}{2(1-p_0)\log \frac{\mu }{\mathit{a\lambda }}}\left(\frac{\mu }{\mathit{a\lambda }}-1\right).\end{array}$$ (95)

Furthermore, $\frac{x-1}{\log x}$ is monotone increasing in x and ${\lim }_{x\to 0}\frac{x-1}{\log x}=0$. Since λ > μ and $\frac{1}{2}\le a\le 1$, we have $0<\frac{\mu }{\mathit{a\lambda }}\le 2$. Hence, we obtain

$$0\le \frac{\frac{\mu }{\mathit{a\lambda }}-1}{\log \frac{\mu }{\mathit{a\lambda }}}\le \frac{1}{\log 2},$$

and we have

$$0\le \frac{p_0}{2(1-p_0)\log \frac{\mu }{\mathit{a\lambda }}}\left(\frac{\mu }{\mathit{a\lambda }}-1\right)\le \frac{p_0}{2\log 2}(1+O(p_0)),$$ (96)

which follows from the fact that $\frac{1}{1-p_0}$ can be written as a geometric series.

Therefore,

$$\begin{array}{lll}A& \approx & \frac{1}{\log a}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}-1\right)-\frac{p_0}{(1-p_0)\log \frac{\mathit{a\lambda }}{\mu }}\\ & & \times \left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log \frac{\mathit{a\lambda }}{\mu }}{\log \mu -\log \lambda }}-1\right)-\frac{1-a}{2a\log a}+\frac{1}{\log \frac{a\mu }{\lambda }}{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}.\end{array}$$ (97)

For C > 0 we obtain $f(x)=\frac{C^x-1}{x}$ is monotone increasing in x, because $f^{\prime }(x)=\frac{1-C^x+C^x\log C^x}{x^2}\ge 0$. Furthermore, we have lim_x→0 f (x) = log C. By choosing $C={\left(\frac{p_0}{1-p_0}\right)}^{\frac{1}{\log \mu -\log \lambda }}$, we see that

$$\frac{p_0}{(1-p_0)\log \frac{\mathit{a\lambda }}{\mu }}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log \frac{a\lambda }{\mu }}{\log \mu -\log \lambda }}-1\right)$$

is negligible compared with

$$\frac{1}{\log a}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}-1\right).$$ (98)

Furthermore, also

$$\frac{1}{\log \frac{\mathit{a\mu }}{\lambda }}{\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}$$ (99)

is negligible compared with (98). Therefore,

$$A\approx \frac{1}{\log a}\left({\left(\frac{p_0}{1-p_0}\right)}^{\frac{\log a}{\log \mu -\log \lambda }}-1\right)-\frac{1-a}{2a\log a}.$$ (100)

A.2 Relative heterozygosity

Proof of Remark 4

Let $f(x,y):=\frac{1}{\frac{1}{x}+\frac{1}{y}}$ for x, y ∈ ℝ⁺. Its Hessian matrix is calculated to be

$$H=\left(\begin{array}{cc}\frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial y\partial x}\\ \frac{{\partial }^{2}f}{\partial x\partial y}& \frac{{\partial }^{2}f}{\partial y^2}\end{array}\right)=\left(\begin{array}{cc}\frac{-2y^2}{{(x+y)}^3}& \frac{2\mathit{xy}}{{(x+y)}^3}\\ \frac{2\mathit{xy}}{{(x+y)}^3}& \frac{-2x^2}{{(x+y)}^3}\end{array}\right).$$

Clearly, we have $\frac{-2y^2}{{(x+y)}^3}<0$ and det H = 0, i.e., the leading minors of H are non-positive. Hence, f is concave but not strictly concave (note that f (x, x) = x/2). Hence, for positive random variables X and Y defined on a probability space (Ω, A, P) and a sub-σ algebra B the Jensen’s inequality for higher dimensions yields

$$\mathrm{E}[f(X,Y)\mid B]\le f(\mathrm{E}[X\mid B],\mathrm{E}[Y\mid B]).$$

Now, choose (Ω, A, P) = (ℕ, P(ℕ), P), where P(j) = α_j. Moreover, choose $X(j)=W_1^{\left(j\right)},Y(j)=(m-1)W_3^{\left(j\right)}$ and B = {0̷, U, T, ℕ}. Then the Jensen’s, inequality gives

$$\begin{array}{lll}\sum _{j\in \mathrm{U}}\frac{{\alpha }_j(m-1)W_1^{\left(j\right)}{W}_3^{\left(j\right)}}{(m-1)W_1^{\left(j\right)}+W_3^{\left(j\right)}}& =& (1-\alpha )\sum _{j\in \mathrm{U}}\frac{\frac{{\alpha }_j}{1-\alpha }}{\frac{1}{W_1^{\left(j\right)}}+\frac{1}{(m-1)W_3^{\left(j\right)}}}=(1-\alpha )\mathrm{E}[f(X,Y)\mid \mathrm{U}]\\ & \le & (1-\alpha )f(\mathrm{E}[X\mid \mathrm{U}],\mathrm{E}[Y\mid \mathrm{U}])=\frac{(1-\alpha )}{\frac{1}{W_1^{(U)}}+\frac{1}{(m-1)W_3^{(U)}}}\\ & =& \frac{(1-\alpha )(m-1)W_1^{(U)}{W}_3^{(U)}}{(m-1)W_1^{(U)}+W_3^{(U)}}.\end{array}$$

Similarly, we obtain

$$\sum _{j\in \mathrm{T}}\frac{{\alpha }_j(m-1)W_1^{\left(j\right)}{W}_3^{\left(j\right)}}{(m-1)W_1^{\left(j\right)}+W_3^{\left(j\right)}}\le \frac{\alpha (m-1)W_1^{(T)}{W}_3^{(T)}}{(m-1)W_1^{(T)}+W_3^{(T)}}.$$

Combination of the above yields

$$\sum _{j=0}^{\infty }\frac{{\alpha }_j(m-1)W_1^{\left(j\right)}{W}_3^{\left(j\right)}}{(m-1)W_1^{\left(j\right)}+W_3^{\left(j\right)}}\le \frac{(1-\alpha )(m-1)W_1^{(U)}{W}_3^{(U)}}{(m-1)W_1^{(U)}+W_3^{(U)}}+\frac{\alpha (m-1)W_1^{(T)}{W}_3^{(T)}}{(m-1)W_1^{(T)}+W_3^{(T)}},$$ (101)

i.e., that ϑ̃^(m) given by (64) is smaller than if it is given by (58).

Clearly in the limit m → ∞ equality holds in (101). Moreover, ϑ̃^(m) → λ. Hence, in the limit case H̃^(m) reduced to the approximation for standard hitchhiking.

The proof is finished by applying the argument formulated above the remark.