Is reasoning from counterfactual antecedents evidence for counterfactual reasoning?

Abstract

In most developmental studies the only error children could make on counterfactual tasks was to answer with the current state of affairs. It was concluded that children who did not show this error are able to reason counterfactually. However, children might have avoided this error by using basic conditional reasoning (Rafetseder, Cristi-Vargas, & Perner, 2010). Basic conditional reasoning takes an antecedent, which like in counterfactual reasoning can be counter to fact, and combines it with a conditional (or set of conditionals reflecting knowledge of how the world works) to draw a likely conclusion. A critical feature of counterfactual reasoning then is that these additional assumptions be modelled after the actual events to which the counterfactual is taken to be counterfactual. In contrast in basic conditional reasoning one enriches the given antecedent with any plausible assumptions. In our tasks basic conditional reasoning leads to different answers than counterfactual reasoning. For instance, a doctor, sitting in the park with the intention to read a paper, is called to an emergency at the swimming pool. The question, “if there had been no emergency, where would the doctor be?” should counterfactually be answered “in the park”. But ignoring the doctor’s intentions and just reasoning on plausible grounds one might answer: “in the hospital”. Only by 6 years, did children give mostly correct answers.

Most studies on counterfactual reasoning in children have focussed on the age at which children are able to give correct answers to counterfactual questions. For understanding children’s reasoning processes the different types of errors that children commit might be more revealing. Unfortunately, in most existing studies the only error children could make was to answer with the current state of affairs (Robinson & Beck, 2000). For example, in the Post Office story used by Riggs, Peterson, Robinson, and Mitchell (1998) the firefighter Peter is at home because he does not feel very well. His wife Sally is out to get some medicine for him. In the meantime Peter gets an emergency call that the post office is on fire. Peter hurries to the post office and children are asked the counterfactual question: “If there had been no fire, where would Peter be?” In principle, children who do not bring to bear counterfactual reasoning might answer with whatever comes to their mind where Peter could reasonably be on the assumption that there is no fire. In this case the two most obvious alternatives highlighted by the story would be: at home and at the post office. Our claim is that, although 4 year old children manage to give the “correct counterfactual” answer “home”, it provides little assurance that they arrived at it by counterfactual reasoning.

For illustrating how “counterfactual” answers were rashly equated with counterfactual reasoning, we use the story by Harris, German, and Mills (1996) in which children were told—and simultaneously observed—episodes such as a doll making dirty footprints on the clean floor and were asked a counterfactual question: “What if Carol had taken her shoes off—would the floor be dirty?” 75% of the 3 year olds and 87% of the 4 year olds gave the correct counterfactual answer “clean”. We argue, however, that this does not necessarily show that children indeed reasoned counterfactually. If they treated the counterfactual question just like an indicative question: “If Carol takes off her dirty shoes and walks without shoes over the floor, is the floor dirty?” they would most likely also answer with “clean” even when completely ignoring the real scenario. In this case they did not reason counterfactually.

From this it becomes clear that children possibly apply different kinds of reasoning. We will show below that the different kinds sometimes lead to the same answer. This means that it can be a fallacy to infer from children’s correct answers to counterfactual questions that they reasoned counterfactually. Perner and Rafetseder (2010) distinguished 2 reasoning strategies that children might apply: There is Basic Conditional Reasoning which consists in the application of a rule to a postulated antecedent. For instance, from common knowledge we know the rule that: “IF someone walks with dirty shoes on a floor THEN the floor is (tends to be) dirty” (conditional premise). If we are now given the actual event that “Carol walks with dirty shoes on this floor” (factual premise) then we can infer from these two premises that: “the floor is dirty.” In this case the factual premise is the antecedent of our rule and this antecedent is provided by reality. This is one instance of basic conditional reasoning called Reasoning about Actual Events (Perner & Rafetseder, 2010). Such reasoning enriches one single model (representation) that reflects the real state of the world. The reasoning itself consists merely of combining this knowledge in form of a conditional rule (IF dirty shoes THEN dirty floor) by universal instantiation with the actual event (dirty shoes) to draw the appropriate conclusion (dirty floor).

If Carol’s walking on the floor is not given as a fact but as an imagined event: “If Carol walks with dirty shoes on this floor,” (imagined premise) then we can conclude, using the same basic conditional reasoning, that “then the floor is dirty.” Since the actual event of the factual premise is replaced by an imagined event it is called Reasoning about Imagined Events. It brings basic conditional reasoning to bear on imagined scenarios. It, too, enriches only one single model but, unlike reasoning about actual events, not one that reflects the actual state of the world but an imagined state of the world.

In order to be able to make all distinctions that are relevant for developmental psychologists, we complicate the example slightly with a second factual premise. This allows for interesting combinations of factual and imagined premises. This time Carol takes her shoes off and walks in her clean socks across the clean floor. After Carol her brother walks across the floor with his dirty shoes. Is the floor dirty or clean? This is just another instance of reasoning about actual events. But if we stop the story after Carol’s crossing the floor and then ask “If now her brother comes and walks with dirty shoes across the floor, will the floor be dirty or clean?” Then we have the case that has been described as Future Hypothetical Reasoning (Riggs et al., 1998) or Reasoning with Imagined Extensions of Actual Events (Perner & Rafetseder, 2010). Children succeed on this kind of reasoning from very early on (Riggs et al., 1998). Although facts are mixed with imagined assumptions, the reasoning still only enriches a single model. It extends the known facts into one possible future development. The contrast to reasoning with imagined events is that future hypothetical reasoning extends the single model into the future while the other one creates a parallel model to reality but this model is independent of reality. Therefore, reality can be ignored for a correct answer when reasoning about imagined events is applied, but if it is not ignored it might interfere with the imagined assumptions and also might lead to a memory overload.

Counterfactual Reasoning requires an additional feature. It also creates a parallel model—like it is the case when reasoning with imagined events—however this model is dependent on reality. Therefore reality can not be ignored but needs to be kept active. This is indicated by questions framed in subjunctive mood with reference to a real event. For instance if we hear of the fact: “Carol walks with dirty shoes on the clean floor and the floor gets all dirty,” then we can ask, “If Carol had taken her shoes off, would the floor be dirty or clean?” Like for reasoning about imagined events the premise here (Carol has taken her shoes off) is an assumption, but one that is counterfactual to the actual event of Carol wearing her shoes and therefore dirtying the floor. The use of the subjunctive indicates that we should assume a scenario (possible sequence of events), in which Carol had taken her shoes off but otherwise things remain the same as in the actual event, except for facts that change by logical necessity or as causal consequence of the counterfactual assumption. In our example that means that we are to assume that Carol took off her shoes, then walked on the clean floor (because she did that in the actual scenario) but without shoes (as a causal consequence of having taken her shoes off). From walking without shoes we can infer that the floor would not be dirty and stay clean—the expected correct answer.

So far, the only characteristic feature of counterfactual problems, which has been emphasised in the developmental literature, is the conflict between the stated premise and the actual state of affairs. Mastering this conflict (not answering with the current state of affairs anymore) is, however, not sufficient for counterfactual reasoning as opposed to basic conditional reasoning. For example, when reasoning about imagined events any assumption about what Carol is doing may conflict with what she is actually doing. Carol may be lying in bed with her clean shoes next to the bed on a sparkling clean floor. When asked “if Carol walks with dirty shoes on the clean floor, is the floor then dirty or clean?” is not a counterfactual question, even though the antecedent in this conditional and the correct answer clearly conflict with what is actually the case. If children can answer this correctly, we have no evidence for their ability to reason counterfactually. The counterfactual element is indicated by the subjunctive: “If Carol were walking with dirty shoes on the clean floor, would the floor then be dirty or clean?” Unfortunately, if children can answer this question correctly, we still have no convincing evidence of counterfactual reasoning ability, because they might ignore the use of the subjunctive and treat it as an indicative question: “If Carol walks with dirty shoes on the clean floor, is the floor then dirty or clean?”, which would yield the exact same answer.

So, we need an inference that rests on at least two premises. One premise is given counterfactually. The other premise needs to be kept the same as in the actual scenario. In a case where the actual event is not the most plausible assumption for the counterfactual scenario, basic conditional reasoning and counterfactual reasoning will yield different answers. For example: “Carol and her brother have dirty shoes. They walk together over the clean floor and the floor is now all dirty.” If we now ask the counterfactual question, “If Carol had taken her dirty shoes off, would the floor be dirty or clean?” the answer is “dirty”, because the brother would still have soiled the floor with his shoes (counterfactuals where the outcome would still have occurred have been called semifactuals (Goodman, 1983)). And we are not supposed to assume that he had taken off his shoes, too, since he did not do so in the real scenario and since it is not a logical or causal consequence of the counterfactual stipulation that Carol takes off hers. In contrast, if we treat the question like an indicative question without regard to what actually happened, i.e.: “If Carol takes off her dirty shoes is the floor then dirty or clean?” one is inclined to answer with “clean”, i.e., a different answer.

At the beginning of this paper we mentioned that children’s correct answers to counterfactual questions might be false positive indications of counterfactual reasoning since they could based on basic conditional reasoning. It has been shown that in Harris et al.’s story children can get the right answer “clean” without thinking about the actual events in the story but by just applying rules from their common knowledge that “floors tend to be clean without dirty shoes”. But this does not work in Riggs et al.’s story. For giving the correct “home” answer children do at least have to take the two possible answers into account: “home” and “post office” (Though it could still be the case that “home” is the most obvious answer when asked out of the blue where somebody is, even when ignoring all the possible answers of the story. But let us set aside this possibility for a moment). Now, the task is to point at the location where the fire fighter would be if no fire had broken out. Even the very young children understand that they have to point to one of the two locations that are suggested by the story world and which they see in front of them. But, to give the correct “home” answer, children also have to understand that the counterfactual question asks them about a location that is different from the current one because when no fire has broken out the firefighter would not be where there is fire. This results simply in an “other than reality” answer.

Now one might be inclined to ask why this does not show counterfactual reasoning. In our opinion we can only conclude from the “other than reality” answer that children do have the ability to integrate reality (where the firefighter is) into their counterfactual assumptions and that they make additional assumptions that the counterfactual questions asks them to give a different answer than reality (overcoming the realist error). But it does not show that they understand that they have to integrate reality in this way. They might do so only because when looking for a suitable additional assumption they happen to think first of something mentioned in the story. This is, however, different from understanding that the counterfactual world has to be build such that only logically or causally necessary changes are to be made to the actual events). Consequently, overcoming the realist error in counterfactual tasks cannot be equated with counterfactual reasoning.

The present paper reports an experiment that investigates whether children’s failure on counterfactual questions is indeed exclusively due to their failure to inhibit what they know to be currently true or whether children also fail because they do not understand that they have to integrate what has really happened in order to give the correct answer. Children were told stories, e.g. about a physician who was either working in hospital (typical location for a physician) or sitting in a park and reading a book (atypical location for a physician) when he was called for an emergency to another location, e.g. the swimming pool. There a boy has slipped, fallen and hurt himself. Overall there were four conditions constructed by varying the number of alternative locations (1 or 2—this is equivalent to one (Carol) vs. two (Carol and her brother) characters in the dirty shoes task) and whether the alternative location, where the main character would counterfactually be, is a typical or an atypical location for that character: 1-typical [1-typ], 1-atypical [1-atyp], 2-typical [2-typ] and 2-atypical [2-atyp]. In the 1-conditions the only error children could make was to answer with where the main character currently was (realist error), as it was the case when children answered with “post office” in Riggs et al.’s task. For example, the scenario in the 1-typ-condition involved a hospital and a swimming pool. The physician got an emergency call in the hospital and then he went directly from the hospital to the swimming pool to attend to little Jacob. Children were then asked “What if Jacob hadn’t hurt himself, where would the doctor be?” Children could correctly answer with “hospital” or they could answer with “swimming pool” which would result in the “realist error”. The scenario of the 1-atyp-condition involved a park (instead of the hospital) where the physician got the emergency call and from where he directly ran to the swimming pool. So, the correct answer would be “park” and the realist error would be again the “swimming pool”.

The idea is that when asked “What if Jacob hadn’t hurt himself, where would the doctor be?” without being told the story one might answer more likely with “hospital” than with “park”. “Hospital” is the common sense answer and most likely to be given by somebody who does not know anything about the actual events of the story (our hypothesis is that children applied this strategy in Harris’s task). If children do indeed make the realist error because they fail to inhibit current reality when asked a counterfactual question, then the salience of reality, e.g. the swimming pool, should matter. In other words, if children fail only because reality is most salient we would expect children to answer mostly with “swimming pool” but there should not be a difference in the amount of errors between the 1-typ-condition and the 1-atyp-condition.

It is, however, possible that children do not have problems with ignoring what is currently the case or what is actually there in front of them but rather with inhibiting a prepotent response which is based on their current state of knowledge about the world, e.g. that doctors work in hospitals. This assumption came up because of a study by Riggs and Peterson (2000) in which children are told that Sally goes to work every day on the short road. But today two men are mending the short road and Sally has to walk along the long road. In the counterfactual to present condition Sally is in the middle of the long road when the two men are finishing their work and the short road is not blocked anymore. Children are asked “If the men had not been mending the road, which road would Sally be walking along?” In the counterfactual to past condition Sally is already at work when the men are removed from the short road. Children are asked “If the men had not been mending the road, which road would Sally have walked along?” There was no difference in difficulty between these two conditions. This supports the idea that children who make the realist error do not have problems with inhibiting a response to a visibly salient feature of the story. Their problems rather stem from not inhibiting what they know to be true. Given that this is in fact the reason why children fail on a counterfactual task this would again mean that there should not be a difference in performance between the 1-typ and the 1-atyp conditions. Children only have to inhibit where the doctor currently is and when they are able to do so they will give the correct answer.

There were two further conditions, the 2-typical and the 2-atypical. The scenarios of both conditions involved a hospital, a park and a swimming pool. This means that children could also make other errors than the “realist error”. In the 2-typ-condition, for example, the physician is at first sitting in the park but then goes to the hospital for work, where he later receives the emergency call to the swimming pool and goes there. The correct answer to the counterfactual question is the typical location, the “hospital”. Wrong answers could be “swimming pool” (realist error) or “park” (atypical error). In the 2-atyp-condition the physician is sitting in the park after work. There he receives the emergency call. He hurries to the hospital to pick up his first aid case and then to the swimming pool to attend to the boy. Here the correct answer is the atypical location, the “park”. Wrong answers could be “swimming pool” (realist error) or “hospital” (typical error). It is of importance that the hospital is not simply a distractor location in the 2-atyp-condition but one that is relevant for the story. Children who understand that they have to create an alternative to reality (a strategy that was successful in Riggs et al.’s task in order to avoid the “realist error”) but who fail to integrate the actual sequence of the story into their reasoning should answer with “hospital”, because this is also an answer somebody would (most likely) give when he/she does not know anything about the actual events in the story. If children answer by default with “hospital”, this happens to be “correct” in the 2-typ-condition but incorrect in the 2-atyp-condition in which “park” would be the correct answer.

From this it becomes clear that children have to meet two criteria in order to answer all conditions correctly. Firstly, they have to create an alternative situation to reality, which is indispensable to avoid the realist error in all four conditions. Basically, children this age should be able to do so (Robinson & Beck, 2000). However, this is not enough for the 2-conditions. Thinking of the location “other than reality” still leaves children with two possibilities, the park and the hospital. Secondly, children have to integrate what has actually happened with what could have happened. If they do not do this, they still can get away with the default assumption that physicians would be in hospital in the 2-typ-condition but fail to give the correct answer in the 2-atyp-condition.

In short, if it is in fact the realist error that masks children’s competence on counterfactual reasoning tasks, then children should even have problems with the 1-conditions. However, if it is also children’s lack of understanding that actual happenings have to be integrated into their counterfactual assumptions, then children should have most problems in the 2-atyp-condition.

Method

Participants

The sample consisted of 133 children (66 boys, 67 girls), from three different nursery schools in the area of Salzburg and Upper Austria, aged between 3;2 (years; months) to 6;10. The children had a mean age of 5;2 with a standard deviation of 12 months. The age of the 56 children in the younger group ranged from 3;2 to 4;11 (M = 4;2, SD = 0;6) and the 77 children in the older group were between 5;0 and 6;10 (M = 5;11, SD = 0;7). For the later display, the overall sample was split into the following ten age groups (n₁ = 14, m₁ = 3;5 ± 0;3. n₂ = 14, m₂ = 4;0 ± 0;2. n₃ = 13, m₃ = 4;4 ± 0;2. n₄ = 14, m₄ = 4;8 ± 0;3. n₅ = 14, m₅ = 5;1 ± 0;3. n₆ = 13, m₆ = 5;5 ± 0;2. n₇ = 13, m₇ = 5;10 ± 0;1. n₈ = 13, m₈ = 6;1 ± 0;1. n₉ = 13, m₉ = 6;5 ± 0;2. n₁₀ = 12, m₁₀ = 6;9 ± 0;2).

Design

Each child was tested in all four conditions (1-typical, 1-atypical, 2-typical, 2-atypical) and the sequence of the different conditions varied from child to child according to a Latin Square Design. Additionally, these four conditions were assigned to four different stories (physician, fire fighter, teacher and policeman) and assignment also followed a Latin Square Design. This resulted in 16 different groups with eight or nine children in each group.

Procedure

Each child was tested individually in one session that lasted about 20 min. As all four stories followed the same structure we use the physician-story as sample-story. At first children were familiarised with the different locations of the story that depended on the particular condition used for the particular child. For the 1-conditions of the physician-story the scenes consisted of the swimming pool (firefighter story: living room; teacher-story: playground; policeman-story: shop) and either the hospital in the 1-typ-condition (fire-station / school / police-station) or the park in the 1-atyp-condition (forest that caught fire / pupil’s home where the teacher took a pupil who had become sick / parking lot where two cars had crashed into each other). For the 2-conditions park (atypical alternative) and hospital (typical alternative) in addition to the swimming pool were used in the physician-story.

In the 1-typ-condition children received the following introduction: “Look! Here you can see a hospital and a swimming pool.”

CONTROL 1: “Can you show me, where the hospital is?”

CONTROL 2: “Can you show me, where the swimming pool is?”

Then the child was introduced to the physician working at the hospital examining a boy lying in bed. Suddenly the mobile phone rang calling the physician to an emergency at the swimming pool. The child’s attention was directed towards the swimming pool: “Oh look, there has been an accident. Little Jacob has slipped and hurt himself—he needs a doctor”. The child’s attention was then directed again to the hospital where the physician got a phone call. He picked up his first-aid case and walked from the hospital to the swimming pool to attend to the little boy. At this point children were asked the following questions:

NOW-CONTROL: “Where is the doctor now?”

For this control question wrong answers were corrected and the story was repeated (at most 2 times), until they answered the control question correctly.

COUNTERFACTUAL: “What if Jacob hadn’t hurt himself, where would the doctor be?”

If children did not respond at all, they were prompted with a forced choice question (counterbalancing the order of options for all versions of all stories), e.g. “Would the doctor be at the hospital or at the swimming pool?”

MEMORY-QUESTION: “Where was the doctor when the emergency occurred?”

In the 1-atyp-condition the physician was reading a book in the park where he received the emergency call. The forced choice option was, “at the park or at the swimming pool” (counterbalanced) and the correct answer to the counterfactual question was “the park” (atypical location for a physician) instead of “the hospital”.

In the 2-typ-condition three locations were used: the swimming pool, the hospital (typical) and the park (atypical). Before work the physician was sitting in the park reading a book. He left the park to go to the hospital for work, where he received the emergency call. The rest of the story followed the version 1-typical, except that the forced choice question was, “at the hospital or at the park?” (counterbalanced)

The 2-atyp-condition was the same as the 2-typ-condition except that the physician was sitting in the park after work reading a book when he received the emergency call. He went to the hospital to pick up his first-aid case and then to the swimming pool. The correct answer to the counterfactual question was the atypical location, the park.

Results

Preliminary Analysis

There was no discernible systematic effect on the number of correct answers regarding the order in which the four different stories were used or in which order the four different conditions were administered. The forced choice questions asked when no answer to the counterfactual question was forthcoming were needed seven times in total and did not have an influence on the number of correct answers either. Further, we examined whether the four different stories were comparable in difficulty. Correct answers to the counterfactual questions were very similar for all the stories: physician-story (73%), firefighter-story (68%), teacher-story (68%) policeman-story (66%), and were not significantly different. Children were almost perfect in answering control 1, control 2, now-control and memory questions (above 98% correct answers in total). They evidently had a good understanding of the story events.

Counterfactual Questions

In all four conditions children could make the realist error by answering with the location where the protagonist really was. In the 2-conditions children could also point erroneously to the location where the protagonist had been but did not intend to stay. In the 2-atyp-condition saying “hospital” instead of “park” resulted in the typical error and in the 2-typ-condition saying “park” instead of “hospital” resulted in the atypical error. An answer was categorised as correct if children answered according to adult counterfactual reasoning, i.e., said “hospital” in the typical conditions and “park” in the atypical conditions.

Children made the realist error in 21% of the time averaged over all conditions (m = .83, S.D. = 1.39, min = 0, max = 4). Frequency of realist errors in the different conditions (1-typ: 17.3%, 1-atyp: 21.1%, 2-typ: 21.8%, 2-atyp: 22.6%) did not differ significantly (Friedman test: χ² (3, N = 133) = 3.7, p = .30, partial eta squared η_p² = .01). This result clearly indicates that the typicality of the alternative location, hospital versus park, did not have an effect on the frequency of the realist errors.

Looking at the other two types of errors, which could only occur in the 2-conditions, children committed the atypical error, saying “park” instead of “hospital”, much less often (11.3%) than the typical error, saying “hospital” instead of “park” (30.1%): McNemar’s χ² (N = 133) = 13.40, p < .001. In other words, children said more often “hospital” when they should have said “park” then they said “park” when they should have said “hospital”. This is evidence that some children tend to make default assumptions, for example, that a physician would be in the hospital if there had been no accident in the swimming pool. These children apparently failed to integrate facts of the actual story event, e.g. that the physician was sitting in the park, reading his book, and intended to stay there. Only, because he intended to stay there, he would be in the park and not in the hospital or elsewhere if he had not been called to the emergency.

Children gave most of the correct answers in the 1-typ-condition (83% correct) and least in the 2-atyp-condition (47% correct). The difference between the 1-conditions was not significant (binomial tests: p = .30). The differences between the 2-atyp-condition and the other three conditions were highly significant: 1-typ: McNemar’s χ² (N = 133) = 41.5, p < .001, 1-atyp: McNemar’s χ² (N = 133) = 33.6, p < .001, 2-typ: McNemar’s χ² (N = 133) = 12.5, p < .001. So, children had the greatest difficulties when there were two alternative locations and the correct answer was the atypical location. 43% of the children who gave the wrong answer in the 2-atyp condition made the realist error but to 57% made the typical error. However, it has to be taken into account that the chance baselines were different between the 1-conditions and the 2-conditions. So, if children were guessing they had a 1 in 2 chance of getting it right in the former, but only a 1 in 3 chance in the latter. Direct comparisons between the 1- and 2-conditions might therefore be not really fair. This is underlined by the fact that performance was above chance baselines in all four conditions (binomial tests: 1-typ: p < .001, 1-atyp: p < .001, 2-typ: p < .001, 2-atyp: p = .001). Still it is worth noting that children performed significantly better in the 2-typ-condition than in the 2-atyp-condition.

Age differences

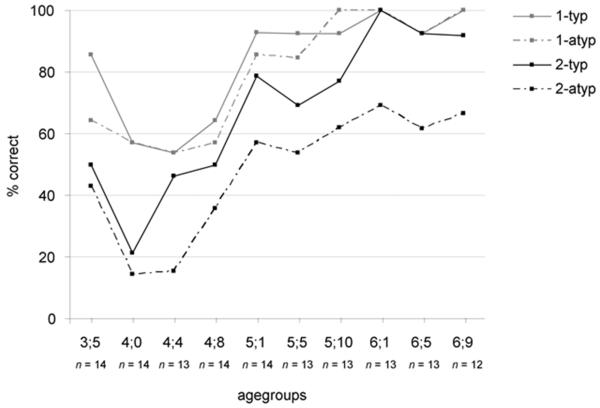
Figure 1 shows performance on the counterfactual questions for the ten age groups in each of the four conditions. Polynomial contrast analysis for the “overall” curve (when the four conditions are averaged: bold line in Figure 1) shows a linear relationship (F (1, 132) = 41.73, MSE = 54.91, p < 0.001) which can be interpreted as a general increase in performance with age, and a cubic relationship (F (1, 132) = 8.29, MSE = 10.91, p = .005). Figure 1 shows that the curve goes down from the age of 3;5 to the age of 4;0, then up from the age of 4;4 to the age of 5;1 and then further up but improvement slows.

Figure1.

Percent correct answers to counterfactual question by condition and age

In order to differentiate children who performed well on single conditions by chance compared to children who showed a good performance across all four conditions we classified them according to their reasoning strategies on the basis of their answer patterns across the four conditions. Overall, fifty children (37.6%) used “counterfactual reasoning”, i.e., they answered with “hospital” in all typical conditions and with “park” in all atypical conditions. Twenty-eight children (21.1%) used “basic conditional reasoning”. They made exclusively typical errors in the 2-atyp-condition but gave the correct answer in the other three conditions. They did not make any realist errors, so they were able to inhibit their knowledge of the protagonist’s actual location. However, these children made common sense background assumptions, e.g. they assumed that the physician would have worked in the hospital if Jacob hadn’t hurt himself, ignoring the fact that the physician had the intention to keep reading his book when he got the phone call. Fifteen of all children (11.3%) were identified as “realists” who made the realist error in all four conditions. They did not consider an alternative situation to reality. The remaining children (30.1%, n = 40) did not show an identifiable reasoning strategy. They were therefore labelled as “mixed”.

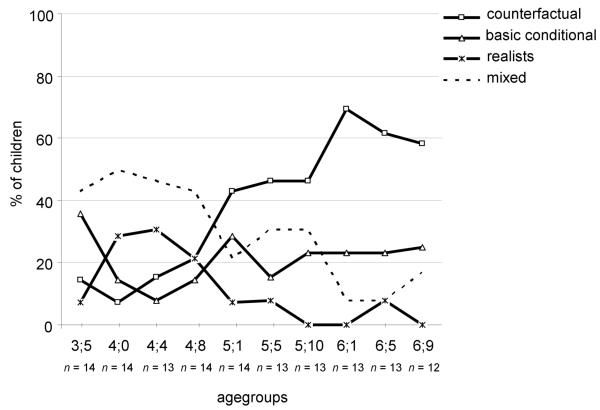
Figure 2 shows the percentage of children who used each of these reasoning strategies per age group. If we compare the younger children (younger than 5) with the older children it turns out that only 16% (n = 8) of the counterfactual reasoners were in the younger group and the remaining 84% (n = 42) belonged to the older group. 39% (n = 11) of the basic conditional reasoners were younger than five and 61% (n = 17) were five or older. Almost all realists (80%, n = 12) belonged to the younger group and only 20% (n = 3) were in the older group. Generally speaking, the amount of counterfactual reasoners and basic conditional reasoners increased from the younger to the older age groups whereas the amount of realists and mixed reasoners dropped.

Figure2.

Percent children using a particular reasoning strategy

Table 1 shows that the youngest children were more likely to pick the typical location in the 2-conditions (which is correct in the 2-typ condition) while they picked the atypical location and the real location with about equal frequency. The 4 year old children preferentially picked the real location. So, the 4 year old children more systematically pointed at the real location (explaining the amount of “realists” in this age group) while the younger children tended to point at the typical location. This can also explain why the 3½ year old children showed a better performance averaged across all four conditions than the 4 year old children. The typical location happened to be the correct answer in the 2-typ-conditions while the real location was never the correct answer.

Table 1.

Frequencies of answers according to condition and age (in percent)

	Age
Condition	m = 3;5	m = 4;0	m = 4;4	m = 4;8	m = 5;1	m = 5;5	m = 5;10	m = 6;1	m = 6;5	m = 6;9
1-typical
Typical	85.7	57.1	53.9	64.3	92.9	92.3	92.3	100	92.3	100
Realist	14.3	42.9	46.1	35.7	7.1	7.7	7.7	0.0	7.7	0.0
1-atypical
Atypical	64.3	57.1	53.9	57.1	85.7	84.6	100	100	92.3	100
Realist	35.7	42.9	46.1	42.9	14.3	15.4	0.0	0.0	7.7	0.0
2-typical
Typical	50.0	21.4	46.2	50.0	78.6	69.2	76.9	100	92.3	91.7
Realist	28.6	64.3	46.1	28.6	7.1	15.4	15.4	0.0	7.7	0.0
Atypical	21.4	14.3	7.7	21.4	14.3	15.4	7.7	0.0	0.0	8.3
2-atypical
Atypcial	42.9	14.3	15.4	35.7	57.1	53.8	61.5	69.2	61.5	66.7
Realist	7.1	57.1	61.5	35.7	7.1	15.4	7.7	7.7	15.4	8.3
Typical	50.0	28.6	23.1	28.6	35.7	30.8	30.8	23.1	23.1	25.0

Note. Those locations that are written in italic were the ones that were correct in the respective condition.

The improvement in performance from the age of 4;4 to the age of 5;1 can be explained with the frequency of realist errors dropping (see Table 1). While the amount of atypical and typical errors does not differ significantly between the two age groups 4;4 and 5;1 (Fisher’s Exact Test: atypical: p = 1.0; typical: p = .68), the amount of realist errors is significantly higher for the younger children in the 1-typ (Fisher’s Exact Test: p = .03), the 2-typ (Fisher’s Exact Test: p = .03) and the 2-atyp conditions (Fisher’s Exact Test: p = .004) but not for the 1-atyp condition (Fisher’s Exact Test: p = .10). The five and six year old children (5;1–6;9) answered with the real location to only 7% of all counterfactual questions. Not committing the realist error resulted in a very good performance in the 1-conditions. In the 2-conditions, the five and six year olds committed the typical and the atypical error in 18% of the cases (averaged), while the three and four year old children did so in 25% of the cases. The reason why younger children did so much worse in the 2-conditions than older children lies therefore in the fact that the younger children showed the realist error in these conditions significantly more often (41%) than the older children (9%): Mann-Whitney test: U (n₁ = 56, n₂ = 77) = 1334.5, p < .001, Cohen’s d = 1.05).

Discussion

In the introduction we outlined that children’s failure on counterfactual reasoning tasks might not only be due to their inability to disengage from reality or from what they know to be true (resulting in the realist error) but also to their ignorance about having to integrate the real events into their counterfactual assumptions. If this is correct, then once children understand that the counterfactual question asks them for a location that is different from the actual location they might still not be able to give the correct answer as long as basic conditional reasoning yields a different answer than counterfactual reasoning.

In summary, our results show that the most frequently used reasoning strategy in 4 year old children is to answer with reality. This goes well with what Riggs et al. (1998) claimed to be the realist error resulting from children’s failure to inhibit current reality. However, our findings complicate this picture because the very young, 3½ year old children use the basic conditional reasoning strategy more often than the “realist” reasoning strategy. So, most of them seem to be able to overcome what Mitchell (1994) called a reality bias.

This finding that realist errors are less pervasive than often thought is also underlined by the fact that they hardly occur in future hypothetical reasoning tasks. Riggs et al. (1998) as well as Robinson and Beck (2000) found that realist errors are much less common in tasks that require future hypothetical reasoning than those that require counterfactual reasoning. In a picture/no picture sorting task children were shown two boxes. One box contained items which had a picture, the other box contained items without a picture. In the future hypothetical version children got a blank piece of paper and were asked: “If I draw on this piece of paper, which box will it go into?” In the counterfactual version the experimenter drew on the blank piece of paper. Once the child had placed the paper in the correct box he/she was asked: “If I had not drawn on the piece of paper, which box would it be in?” The 3;5 to 4;4 year olds answered 89% of the future hypothetical questions correctly while they only answered 43% of the counterfactual questions correctly (Riggs et al., 1998).

One problem with this interpretation, however, is that the current reality is not matched in these two versions. While in the counterfactual version the piece of paper has had a picture drawn on it and has been sorted into the “picture box” this was not the case in the future hypothetical version. Here the paper did not have a picture drawn on it and it has not been sorted into a box when the child was asked the question. This problem has been solved by Robinson and Beck’s car task. In this task children saw a road with a garage on either side. Then they watched a car running down the road and parking in the lower garage. In the counterfactual version children were asked “What if the car had driven the other way? Which garage would it be in?” In the future hypothetical version they were asked “What if next time the car drives the other way? Which garage will it be in?” Although the current reality was the same in both versions children found the counterfactual task (77% correct) significantly harder than the future hypothetical task (94% correct). This suggests that it is not the inability to ignore reality that makes the counterfactual task more difficult than the future hypothetical task.

Therefore, the question remains why children perform better in the future hypothetical task than in the counterfactual task. Rafetseder, Cristi-Vargas, and Perner (2010) stated that in the counterfactual condition there is a conflict between reality and the counterfactual assumption while this is not the case in the future hypothetical condition, where reality is just extended into the future. This can be explained with the help of the linguistic mood. The indicative, which is used in future hypothetical tasks, signals the start of a new, unrelated assumption. Similarly the subjunctive refers to an assumption, but to one that is negated to what has been actually happening. So both, the indicative and the subjunctive conditional, refer to a possible sequence of events, but only the subjunctive signals that these possible events have to be related to the real events (Perner, 2000). Thus, one needs to remember what has happened only for the counterfactual task but not for the future hypothetical task. Holding multiple possibilities in mind poses a problem per se for children (Beck, Robinson, Carroll, & Apperly, 2006). This suggests that it is the complexity that makes the counterfactual task more difficult than the future hypothetical task.

A study that controlled for complexity was done by Schaller (2004). The setup showed a house and two stations (A and B). From station A a bus goes to the mountains (M) and a train goes to the lake (L). At station B it was reversed: a bus goes to L and a train to M. In the counterfactual version 3 to 5 year old children (n = 24; m = 4;2; S.D. = 0;6) saw Peter going to station A and taking the bus to M. Then they were asked: “Peter goes to station A and takes the bus to M. What if he had gone to station B and had taken the bus from there, where would he have arrived?” In the future hypothetical version children again saw Peter going to station A and taking the bus to M. But this time they were also introduced to Susi and were asked: “What if Susi walks to station B and takes the bus from there, where will she arrive? Will she then be where Peter is or will she be somewhere else?” Children performed similar in both conditions. This supports the hypothesis that when the future hypothetical task is made more complex (children had to hold in mind where Peter was and where Susi will be in relation to Peter) then the difference between counterfactual and future hypothetical conditions vanishes.

To summarise, children find counterfactual tasks more difficult than future hypothetical tasks only when they are more complex, e.g. because they have to hold in mind two possibilities. When complexity is comparable, performance on these tasks is similar. So the fact that children have more problems with some counterfactual tasks is not inconsistent with our claim that both—the counterfactual and the future hypothetical tasks—are solved by basic conditional reasoning. It is only the complexity of the task that creates a difference in performance.

One compelling explanation of our pattern of results might lie in the very young children’s inability to interpret the relevant part of the counterfactual question, “…, where would the doctor be?” The youngest might gloss it simply as, “Where is a doctor (usually)?” That is why the 3½ year olds answer with the hospital (typical location error) when this option is available or else with the doctor’s actual location. Four year olds realise that such a general reading is inappropriate and that the question is about this doctor’s (present) location. Yet, they still fail to appreciate the imagined character of the antecedent conditional and, therefore, answer with the actual location (realist error). Older children start to appreciate the imagined impact of the “if” antecedent and understand that the question most likely asks for a location that is different from reality. Therefore, these 5-year old children hardly commit the realist error. However, if there are two alternatives to the real location they tend to pick the typical location for a doctor (basic conditional reasoning) or any one of them (mixed), some of which hit with luck both times on the “counterfactual” option. Only by 6 years does the counterfactual reasoning strategy become dominant (and cannot be explained by fortuitously picking the counterfactual answers of the two alternatives).

What becomes clear from this is that there are several basic problems for children to overcome. (i) Especially the youngest children might first of all suffer from linguistic limitations in interpreting subjunctive conditionals (Beck, Riggs & Gorniak, in press). It is also possible that children find the subjunctive per se difficult. However, experimental findings by Au (1992) do not support this. Four year old children were invited to think of some pretend situations, e.g. let’s pretend this straw is a pencil. In the Subjunctive Condition children were asked the question “If this were a pencil, what could you do with it?” while in the Simple Conditional condition the question was “If this is a pencil, what can you do with it?” All children responded appropriately on all questions regardless of whether the question was phrased in the subjunctive mood or in the indicative mood. (ii) Another major problem is coping with the interference between the real sequence of events and the counterfactually assumed sequence. We have already mentioned that future hypothetical reasoning extends the single model into the future while counterfactual reasoning creates a parallel model to reality. So, the problem might not have to do with inhibition but more with how children interpret of what the question refers to. Future hypothetical reasoning tasks clearly refer to future locations while counterfactual reasoning tasks refer to present locations. When asked a counterfactual question children might be confused whether they should answer with the present location in the real world (resulting in the realist error) or with the present location in the possible world (resulting in the correct answer). (iii) By around 5 or 6 years children do accept that there can be multiple possibilities (behavioural undetermined trial, Beck, et al., 2006). However, keeping two models of the world in mind might lead to a substantial working memory load.

One remaining question is what our data add to the existing literature. Our suggestion that children give correct answers based on basic conditional reasoning opens up a new venue of explanation for data reported in the literature. It is related to the idea that it matters how many inferential steps are required (German & Nichols, 2003). However, the drop in likelihood of success with longer inferential chains is not considered the result of working memory overload. Beck, Riggs, and Gorniak (in press), who failed to replicate German and Nichols’s result, found that children’s patterns of answers could be predicted by their linguistic ability. German and Nichols’s findings could also be explained with the fact that the likelihood diminishes with each additional step that all of the required default assumptions match the “nearest possible world” constraint. For example, in Harris’s task children are asked “If Carol had taken her shoes off, would the floor be dirty?” This directly triggers the knowledge that with shoes off floors stay clean and the correct answer follows with high probability, say, p = .75 at age 3½ (rough estimate from the actual data) with a reality bias of .25, and p = .9 at 4½ with the reality bias reduced to p = .1. The relevant knowledge is not triggered that directly in Riggs et al.’s task. The question “If there had been no fire, where would Peter be?” only activates the knowledge that without fire firemen could be anywhere. Now, let us assume, as we did above for the Harris et al. scenario, that at about 3½ years the reality bias is p = .25. Then with probability p = .75 children will opt for any of the locations mentioned in conjunction with Peter: home or post office (which is on fire). These children will pick one of them for their answer with some probability, say each with p = .5. Combined with children’s reality bias this will result in 62.5% “post office” and 37.5% “home” responses at 3½ years (in fact in Riggs et al. second experiment the slightly older 4 year olds gave 47% “home” answers).

Another question is why children get better with age before they start to use counterfactual reasoning at 5 to 6 years. One reason is that their reality bias diminishes, which we assume is the main reason for improvement on the tasks by Harris et al., e.g., by age 4½ it is down to about p = .1 and children are almost perfect in their answers (87% correct in Exp. 1). With this reality-bias estimate our theory would then predict still only 45% correct “home” responses in the study by Riggs et al. (1998; Exp. 4 with 4½ year olds: 43%). With the reality bias practically at zero no further improvement would be expected until children begin to reason counterfactually. Riggs et al. do not provide data for older children. However, plausibly, older children will come up with more elaborated assumptions, e.g., that people are rather at home than at the post office (when there is no fire). Such assumptions lead to the correct “home” answer even though children are applying basic conditional reasoning. Admittedly all these good matches to actual data are somewhat serendipitous since they depend on the expedient setting of choice probabilities at .5—but they only serve to illustrate how the assumption that children use basic conditional reasoning in counterfactual tasks is compatible with observed data.

One point that still needs to be addressed is how our findings relate to the wider work on reasoning. One critical feature of counterfactual reasoning, Lewis (1973) tried to capture formally in his “nearest possible world” constraint. The “nearest” captures the fact that the counterfactual scenario needs to be maximally similar to the real scenario. The “possible” captures the fact that the new scenario must stay logically coherent, or else it would describe an impossible world. However, there is still debate over the logical adequacy of Lewis’s criterion, especially concerning the highly metaphysical notion of possible worlds. A far less metaphysical account has earlier been proposed by Stalnaker (1968). Stalnaker extended the Ramsey test, which has initially been developed as a psychological account of indicative conditionals (“if A then B”), to counterfactual conditionals. Ramsey (1931/1990, p.247) argued that—when people evaluate “if A then B”—they assume A hypothetically and then make judgments about the conditional probability of B given A (P(B|A)). Supportive evidence comes from Over, Hadjichristidis, Evans, Handley, and Sloman (2007, p. 64) who found that people’s subjective judgment about P(if A then B) is the same as their subjective judgment about P(B|A). This was the case for both, indicative and counterfactual conditionals and suggests that people make similar judgments about indicative and counterfactual conditionals as well. And it fits with the account that indicative and counterfactual conditionals differ only in their temporal aspect (Bennett, 2003; Edgington, 1995; Evans & Over, 2004). The idea is that for counterfactuals people have to go back to a point in time to which the counterfactual antecedent is the counterfactual alternative and then apply the same (future hypothetical) reasoning they would have used at that time if the actual events had been as given by the counterfactual antecedent. Thus, the counterfactual requires an extra step in processing which has to do with placing oneself mentally at the earlier time.

According to this view people have to (1) find the correct time point in the past and then (2) apply reasoning with indicative conditionals when they are asked a counterfactual question. The claim that people have to apply a similar psychological process to counterfactual and indicative conditionals but at the different time point (for counterfactuals in the past and for indicatives in the present), however, strikes us as controversial in light of examples that were used in developmental work. For example, in a study by Rafetseder et al. (2010) children were told about Simon and his little sister Julia. They both like sweets and their mother sometimes puts some sweets into a cupboard, either on the top or the bottom shelf. Simon is able to reach only the top shelf because of an injury he is not able to bend down to reach the bottom shelf. Julia, in contrast, is too small. She is only able to reach the bottom shelf but not the top shelf. Whenever Julia finds sweets on the bottom shelf she brings them into her room. Whenever Simon finds sweets on the top shelf he brings them into his room. Let’s assume that children have just watched that sweets were put onto the bottom shelf and that little Julia had come to bring them to her room. Then children are asked “But what if sweets had not been on the bottom but on the top shelf, where would the sweets be?” If children now apply a similar reasoning to counterfactual conditionals as they do to indicative conditionals this would mean that they first have to find the correct starting point, e.g. the point where it was still possible that sweets were put either on the top or on the bottom shelf. In our example this is the point when mother is deciding where to put the sweets. Then they have to apply reasoning with indicative conditionals: ”Where will the sweets be if they are put on the top shelf?” (parallel to the counterfactual question: “Where would the sweets be if they had been put on the top shelf?”). However, unlike in the counterfactual case, the indicative leaves at least two plausible answers, e.g.: “on the top shelf”, or “in the boys room” depending on what might happen: if no one comes then top shelf, if the girl comes, too, and if the boy comes then in his room.

In contrast, when reasoning with counterfactual conditionals our and 81% of normal adults’ intuition (Rafetseder et al., 2010) is that there is a single correct answer. This means that when asked “Where would the sweets be if they had been put on the top shelf?” one should assume not only that sweets had been put onto the top shelf but also take on board the fact that the girl had come in search of sweets, and not leave this open as one would have to in the indicative future case. From this it follows that there is only one correct answer: “sweets would have stayed on the top shelf,” since little Julia would have come in search of the sweets and not be able to take them with her.

Interestingly, most children and some adults do, in fact, not take the searcher (events after the counterfactual change) as fixed by the real events. Even at 12 to 14 years 56% of children (Rafetseder & Perner, 2009) and 19% of adults (Rafetseder et al., 2010) thought that then the sweets would be in the boy’s room. This fits with the suggestion by Over et al (2007) that once participants find the right starting point they apply reasoning with indicative conditionals. One piece of evidence against this in adults are their explanations. They said that they knew that the sweets would have stayed on the top shelf (so they took it for granted that the girl would have been the searcher) but since they stay on the top shelf the boy would have come by later to get the sweets. We do not have any explanations from children about why they thought that the sweets would be in the boy’s room. This leaves the intriguing possibility that children between 12 and 14 years come to realise that events before the counterfactual change have to be modelled after the actual events, but only after 14 years do so for events that occurred after the counterfactual change.

Children may also have problems interpreting if-then statements as conditionals. Barrouillet, Gauffroy, and Lecas (2008) as well as Gauffroy and Barrouillet (2009) describe a developmental change starting around 8 years on how they evaluate the four truth table cases of “if A then B”. The younger children begin with a conjunctive interpretation, where they consider the AB case as true but all the other cases as false. Only from 15 years on do they interpret the conditional as true for the A and B case, as false for the A and ¬B case and as indeterminate for the ¬A and B and the ¬A and ¬B cases. This is exactly how adults interpret “if A then B” (Over et al., 2007). However, conjunctive interpretations have also been found in adults (Evans, Handley, & Over, 2003; Oberauer & Wilhelm, 2003). A recent study by Fugard, Pfeifer, Mayerhofer, and Kleiter (2010) suggests that many adults who start with a conjunctive interpretation on a probabilistic truth table task shift towards a conditional interpretation as the task progresses.

The fact that even 8 year old children tend to give the conjunctive interpretation means, that the children in the present study might have solved the task simply by thinking of the counterfactual question “What if Jacob hadn’t hurt himself, where would the doctor be?” as a conjunction. The idea is that children know that doctors tend to be in hospitals unless there are special reasons to be elsewhere, e.g., If there is no accident, then doctors are in hospitals (A = no accident; B = doctor is in hospital). According to the dual process accounts (Barrouillet et al., 2008; Evans, 2006) the counterfactual question should only trigger the initial model in which there is no accident and the doctor is in the hospital. In this case children should only admit “no accident and doctor in hospital” as true. This could explain why the children found especially the 1-typ condition easy because only the hospital is compatible with their initial model given that no accident has happened.This explanation fits for the very young children in our study. They answered most often with hospital when there was one in the story world, otherwise they answered with where the doctor really was. But at the same time the majority of children did not follow that interpretation, e.g. the ones that committed the realist error (majority of the 4 year old children) and the ones who answered with “park” in any of the three conditions where park was an option.

Conclusion

Most of the research concludes that counterfactual reasoning emerges between 3 and 5 years, while a few studies—mostly working with counterfactual emotions (Amsel et al., 2003; Guttentag & Ferrell, 2004) —point at the later age of 6 years or older. Our guiding hypothesis is that the studies with the younger children document that children can engage in basic conditional reasoning when premises and conclusions contrast with reality. While the studies with older children may get at children’s ability to obey Lewis’s “nearest possible world” constraint by being able to systematically relating the counterfactual scenario to the real scenario.