Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2011 Dec 21;1:202. doi: 10.1038/srep00202

“Magnetic Force Microscopy and Energy Loss Imaging of Superparamagnetic Iron Oxide Nanoparticles”

Bruno Torre 1,a, Giovanni Bertoni 1,2, Despina Fragouli 3, Andrea Falqui 1, Marco Salerno 1, Alberto Diaspro 1, Roberto Cingolani 1, Athanassia Athanassiou 3
PMCID: PMC3244111  PMID: 22355717

Abstract

We present quantitative, high spatially resolved magnetic force microscopy imaging of samples based on 11 nm diameter superparamagnetic iron oxide nanoparticles in air at room temperature. By a proper combination of the cantilever resonance frequency shift, oscillation amplitude and phase lag we obtain the tip-sample interaction maps in terms of force gradient and energy dissipation. These physical quantities are evaluated in the frame of a tip-particle magnetic interaction model also including the tip oscillation amplitude. Magnetic nanoparticles are characterized both in bare form, after deposition on a flat substrate, and as magnetically assembled fillers in a polymer matrix, in the form of nanowires. The latter approach makes it possible to reveal the magnetic texture in a composite sample independently of the surface topography.

Nanoscale magnetic materials play a central role in many areas of science and technology1, such as high density data storage2, development of advanced materials3,4, and biomedical devices for cancer hyperthermia therapy, drug delivery and rapid cell sorting5,6,7. While nanoscale reduction of the particle size is a common requirement for most applications, different magnetic properties have to be designed for specific tasks: e.g., in mass memory devices each data element should exhibit stable magnetization at room temperature (RT)8. On the other hand, biomedicine, nanocomposite and ferrofluid applications9 rely on colloidal dispersion of the magnetic nanoparticles (NPs), for which one should avoid uncontrolled agglomeration, precipitation or segregation in the fluid medium10,11,12 by reducing the long–range interparticle forces. To prevent aggregation in solution, two particles at distance s must have permanent magnetic moment mm such that the magnetic interaction energy is lower than the thermal energy, i.e. 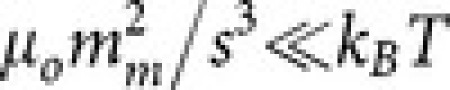Inline graphic, with µ0 the medium magnetic permittivity, kB the Boltzmann’s constant, and T the absolute temperature. Since, in first approximation, mm is proportional to the NP volume, aggregation can be avoided by keeping the NPs sufficiently small and their distance sufficiently large by means of non magnetic coatings13. At reduced size, magnetic properties of individual particles are also affected by surface states due to the high surface to volume ratio, and also the particle shape becomes important. Therefore, magnetic NPs assemblies have to be investigated by means of a technique capable to record magnetic and topography texture simultaneously at both high magnetic sensitivity and nanometer spatial resolution.

Magnetic Force Microscopy (MFM)14,15 can match both requirements, since it provides the nanometer resolution typical of dynamic atomic force microscopy (AFM), making single particle studies possible. In the last decade MFM in ambient conditions has undergone a renewed interest, thanks to an increased sensitivity obtained by technical advances in low noise detection electronics, coupled with external magnetic fields applied on the samples. Environmental MFM studies of submicrometric structures have been first carried out on NP clusters inside magnetotactic bacteria16 and in arrays of 150 nm size ferromagnetic Co nanostructures17, having permanent magnetization at RT.

When the individual magnetic particles are smaller than the magnetic domains in bulk material, permanent magnetization at RT is no longer found and each NP exhibits a paramagnetic-like behavior characterized by a high induced moment, called super-paramagnetic (SP) state. The instantaneous magnetic moment of each SP NP is continuously undergoing stochastic inversion between opposite directions. The Nèel-Brown model18 for uniaxial spherical particles describes this physical process by a spin relaxation time, representing the average time for a NP magnetic moment to flip along the easy magnetization axis. This process is thermally activated, with exponential dependence on the particle magnetization and thus on its volume, as described by the Arrhenius law1. As a result, small changes in NP size can lead to very different magnetic properties at RT. The SP state is of interest since the non-magnetic particles can still be magnetized by an external field, which will favor one of the two opposite easy magnetization directions, leading to a stable magnetic configuration as described by the Stoner-Wohlfarth model18,19. In this way, field controlled SP NP assemblies can be induced in a colloidal dispersion13,20,21. Additionally, shape, size and magnetic properties of the assemblies can be tuned by controlling particle size and magnetic field5,22,23,24. Typical diameters at which a magnetic material exhibit SP behavior at RT are of few tens of nanometers. For γ-Fe2O3 iron oxide, a relaxation time of 100 s corresponds to a 55 nm particle diameter, as obtained by using a power law fit13 of the anisotropy constants measured by Fiorani et al.24. Recently, Rasa et al.25 investigated the magnetic contrast between individual SP magnetite NPs, calculating the magnetic signal expected for differently shaped tips coated with 50 nm CoCr, and concluding that only particles with diameter >15 nm could be magnetically imaged. Similarly, for a 60 nm CoCr coated tip a minimum particle diameter of 10 nm was calculated by Agarwal et al.26, who could experimentally detect (17±7) nm diameter NPs with the help of an external magnetic field. In both cases van der Waals forces, competing with the magnetic signal, were observed. These long-range forces have been further investigated using magnetized tips on gold, silica and iron oxide particles by Neves et al.27, who found opposite phase lag for magnetic and non-magnetic materials and concluded that this effect can be used to distinguish the two different types of interactions, respectively. Recently, very high sensitivity has been demonstrated by Dietz et al.28, who detected the magnetic signal from single ferritin molecules in liquid using a multifrequency method based on harmonic distortion analysis, yet with difficult data interpretation29,30,31,32.

In this work we obtain a better understanding of the resolution limits in imaging SP NPs by addressing both the theory and the experimental practice of the two-pass technique, and demonstrate quantitative magnetic imaging. For this aim, two types of magnetic nanotextured samples were prepared from solutions of ∼11 nm diameter γ-Fe2O3/Fe3O4 colloidal NPs. The first consists of NPs aggregated upon fabrication of a film, which exhibits compositional uniformity across its surface, ensuring uniform van der Waals forces giving a constant long range contribution over the whole sample, as discussed in the supplementary information session. The other type of sample is a regularly textured nanocomposite, in which prior application of an external magnetic field results in the NPs assembly into elongated stripes inside the polymer. The magnetic NP stripes appear both at the surface and in the bulk of the nanocomposite, providing us with a benchmark for testing MFM imaging not coupled with topographical features.

Results

Theory of MFM

In the MFM literature there is no univocal choice of the oscillation parameters best representing the magnetic signal, since these are not independent from possible additional non-magnetic long-range interactions. Some authors focus their attention on the resonance frequency shift25, oscillation amplitude26 or oscillation phase lag26,33,34,35,36. In general, amplitude, phase and frequency shift signals are not independent, and in single harmonic oscillator model they are related through the slope of the resonance peak i.e. the cantilever quality factor Q. However, Q is also affected by dissipative tip-sample interactions, including compositional and mechanical information (e.g. plasticity)37. We use separately the frequency shift signal to evaluate the tip-sample magnetic interaction, resulting in a force gradient channel, and a combination of phase and amplitude signals to give a quantitative measurement of the inelastic interaction, resulting in an energy loss channel38,39.

The frequency shift allows the direct measurement of the force changes with no need to introduce measurement sensitive parameters such as Q. In the single harmonic oscillator approximation, the force gradient is25:

graphic file with name srep00202-m1.jpg

where Fz is the vertical component of the force pointing out from the surface, ν0 is the free resonance frequency, k is the cantilever spring constant, and Δν is the frequency shift.

Phase lag and amplitude signals are combined to calculate the energy dissipation in each oscillation cycle40 due to the inelastic part of the tip-sample interaction, hereafter called energy loss EL:

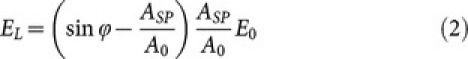graphic file with name srep00202-m2.jpg

where 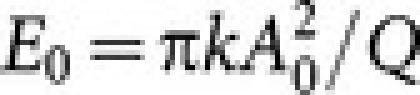Inline graphic, with A0 the free oscillation amplitude far from the surface, ASP the actual oscillation amplitude (ASP1 for first pass and ASP2 for the second pass), and ϕ the phase lag between dither signal and tip oscillation, assuming ϕ0 = π/2 for free oscillation. By considering a single magnetic NP interacting with a magnetic tip in a dipole-dipole model25:

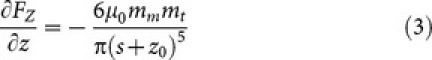graphic file with name srep00202-m3.jpg

where mm and mt are the magnetic moments of particle and tip (in our case mm = 3*10−19 Am2 and mt = 1*10−16 Am2 respectively), s is the tip-particle surface-to-surface distance, and z0 is an additional distance accounting for the position of the magnetic dipoles within particle and tip. For a tip of diameter dt and a NP of diameter dm, z0 = dm/2+dt/2+d0, where d0 is the thickness of a passive layer at the NP surface (figure 1). The term d0 can represent a coating of organic capping molecules13 such as in the present case, or of silica41 or other non-magnetic and non interacting materials1,6.

Figure 1. Simplified sketch of the tip-particle magnetic layout in a dipole-dipole model, indicating the different distance terms (not at scale).

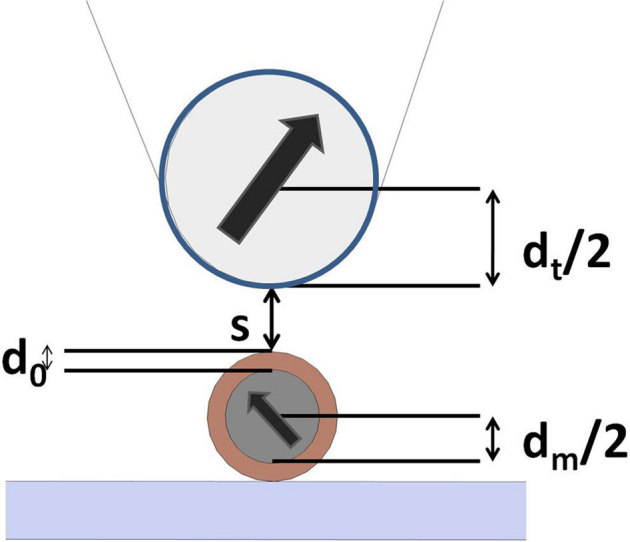
Figure 1

Open in a new tab

Magnetic dipoles (black arrows) are modeled as located in the center of a SP NP having diameter dm and in the center of a sphere with diameter dt approximating the tip apex, while d0 represents the thickness of a non magnetic layer on the particle. Therefore in this scheme the dipole-dipole distance is easily obtained adding z0 = dm/2+dt/2+d0 to the physical distance s.

The effect of tip oscillation on the magnetic signal has never been modeled so far. However, by using a modified version of equation 3 one can calculate the dependence of the force gradient due to magnetic interaction on the tip oscillation amplitude ASP2 and elevation H during the second pass, as the two parameters to be optimized during MFM measurements. The tip position s contains both a static and a time modulated part: s = H+ASP2+ASP2 sin(ωt), where H = H0+(ASP2-A0). Due to the modulation of s, the tip will probe a higher force during the approaching half-cycle of each oscillation and a lower force during the retracting one. Consequently, the effective force gradient averaged over a whole oscillation cycle becomes:

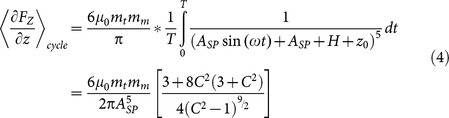graphic file with 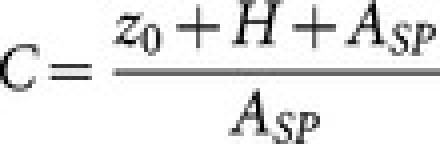name srep00202-m4.jpg

with Inline graphic (see figure 2a). Therefore, with respect to the static case of equation 3 at the same average position25, a correction factor γ is required for the force gradient:

graphic file with name srep00202-m5.jpg

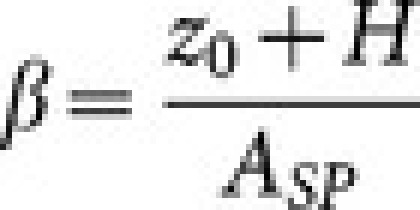where Inline graphic (see figure 2c). In the limit of small oscillations or very far from the surface (i.e. for β→∞) it is γ→1, since the oscillation amplitude will be negligible with respect to the average height, falling into the static case25. The averaged formula for the van der Waals long range interaction term and its relative weight with respect to the magnetic one is discussed in the supplementary information session.

Figure 2. (a), (b) expected force gradient and energy loss for an 11 nm diameter iron oxide particle, calculated for tip parameters as reported in equations 4 and 7.

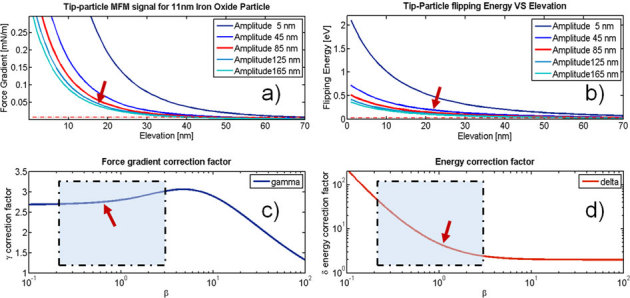
Figure 2

Open in a new tab

The dashed line indicates the thermal noise level in our setup. (c), (d) force gradient and energy loss correction factors γ and δ, respectively, as a function of parameter β, calculated from equations 5 and 8, respectively. The red arrows in figures (a), (b), (c) and (d) show the expectation values for MFM signals for H = 20 nm and oscillation amplitude A0 = 85 nm (red curves in (a) and (b)), corresponding to a value of β = 0.85. The light blue squares in figures c and d indicate the common working conditions for most commercial cantilevers.

Similarly, the energy loss signal can be compared with the maximum energy transferred between the tip and a SP particle. In dipole interaction approximation it corresponds to the energy needed to invert the particle moment:

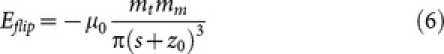graphic file with name srep00202-m6.jpg

By averaging over a tip oscillation cycle:

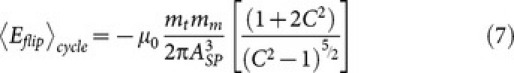graphic file with name srep00202-m7.jpg

Therefore, with respect to the static case in equation 6, for the energy dissipation a correction factor

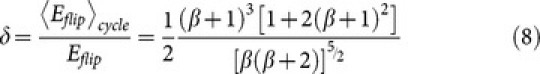graphic file with name srep00202-m8.jpg

is required (see figures 2b and 2d). This general formulation can also be applied to negative H values, by considering the proper ASP2. For H>A0-ASP2, as in our case, it is ASP2≈A0.

For force gradient, the noise is:

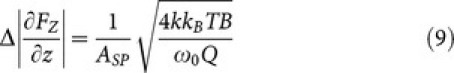graphic file with name srep00202-m9.jpg

where T = 300 K is the RT and B = 2 kHz is the input bandwidth of the detection system42. In our case this noise level is 0.01 mN/m, shown in figure 2a as a red horizontal dashed line, which is much lower than the force gradient calculated for different oscillation amplitudes. Similarly, a red dashed line indicating the thermal noise level 1/2 kB T ≈ 12 meV is drawn in figure 2b. As expected, better signal to noise values are found in the small oscillation regime, since the average tip-sample distance ASP+H can be greatly reduced, while still respecting the condition H>A0-ASP.

Figure 2c shows the dependence of the force gradient correction factor γ as a function of β. As shown, it is always γ≥1. Specifically, at oscillation regimes with e.g. β<50 the resulting sensitivity is significantly higher than in the static case of equation 3. Similarly, as shown in figure 2d, δ is always ≥1, indicating that sensitivity on the energy loss channel is always improved. For β≤1 the correction factor strongly increases, while for a reduction of H to few tens of nanometers, δ can be increased of almost one order of magnitude.

Magnetic nanoparticles

In figure 3 the STEM and HRTEM images of the colloidal magnetic NPs drop casted on an ultrathin carbon grid are presented. The NPs have spherical shape and are monodispersed in size with a diameter of (10.9±1.7) nm, as shown in figure 3a. HRTEM data reveal the single crystal structure of each particle core, and the existence of a capping layer (figure 3b) with thickness δ∼0.85 nm, attributed to the oleic acid (OLAC) used during the wet NPs synthesis13.

Figure 3. (a) high angle annular dark field (HAADF) STEM image of iron oxide NPs.

Figure 3

Open in a new tab

(b) Elastic filtered HRTEM image of a group of NPs, showing the crystalline cubic structure (inset). The OLAC capping (δ∼0.85 nm thick) surrounding each particle has been pointed out by the dashed circles.

The previous theoretical considerations allow for optimum choice of the MFM working parameters. Samples of such colloidal NPs drop casted from diluted solutions and imaged by MFM are displayed in figure 4. The force gradient (figures 4b, 4e) and energy loss data (figures 4c, 4f) are collected in NAP mode, with H = 20 nm and ASP2≈A0 = 85 nm, to ensure a complete decoupling between short-range (topography) and long-range interactions.

Figure 4. (top) 5 μm size images of sparse nanoparticles film: (a) topography, (b) force gradient, (c) energy loss derived from measured signals according equations 1 and 2.

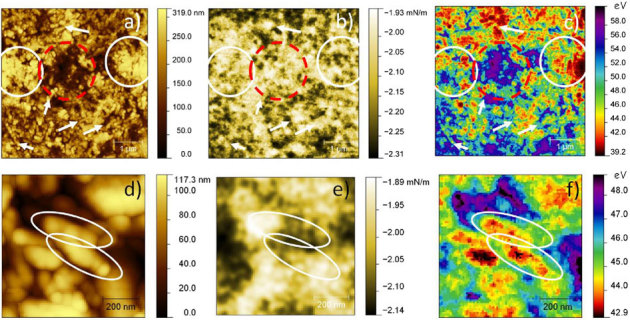
Figure 4

Open in a new tab

Color bar for (b) and (c) is expressed in physical units of mN/m and eV, respectively. (bottom) close-up of previous images: (d) topography, (e) force gradient, (f) energy loss of aggregates formed due to long range interactions (NAP mode); (f) detail of the energy loss image acquired during second pass highlighting a good contrast on different particles within each linear structure. The white and red circles in figure (a), (b) and (c) show a comparison of topography, force gradient and energy dissipation in the regions corresponding to hills and valleys, demonstrating lack of correlation between topography and magnetic signals (see text). White arrows in figures (a), (b) and (c) indicate topography and magnetic signals measured in correspondence of elongated NP aggregates, revealing the inner magnetic texture in correspondence of aligned particles, also shown in magnified figures (d), (e), and (f) within the white elipsoids.

Figure 4a shows the typical sample topography acquired during the first pass. Elongated assembly of spherical particles with typical width of few (1–2) particles and length up to some tens (typically 3–10) are visible (see white arrows). Several features corresponding to single particle size in both directions also appear, which can be associated to either individual particles sitting on the top surface or elongated one-dimensional particle aggregates aligned vertically to the substrate. Autocorrelation length calculated the for topography image gives ∼25 nm size of the smaller geometrical features, which also resembles single particle diameter after slight increase due to tip convolution effect43. In addition to the small NP aggregates, a micrometer sized wavy background is observed, which originates from the multilayer nature of the NPs film, resulting in alternating hills and valleys (red dashed and white circles, respectively).

In figures 4b and 4c the measured maps of magnetic (force gradient) and inelastic interactions (energy loss) are reported, respectively, as derived from second pass signals (amplitude and phase in AM mode and frequency in FM mode) acquired in NAP mode at the same elevation of H = 20 nm. Figure 4b has been calculated according to equation 1. High values of tip-sample magnetic interactions are obtained both in thicker and thinner regions, corresponding to bright and dark areas in figure 4a, enclosed in the white and red circles, respectively. This demonstrates that the magnetic contrast detected during the NAP pass is independent of the topography. In both depressed and elevated regions of the sample, alternated domains of strong (light) and weak (dark) magnetic force gradient also appear in figure 4b. In this case an autocorrelation analysis reveals a dominating size of ∼250 nm, corresponding to the average magnetic domain diameter, hundreds of times larger than single NP, indicating long-range ordering of the NP magnetic dipoles44.

In figure 4c an energy loss map calculated according to equation 2 is presented. Previous studies have demonstrated how energy loss imaging in tapping mode can provide high compositional sensitivity39. Here, this calculation is applied for the first time to the MFM interaction far from the surface (NAP mode), which highlights its dissipative part. In figure 4c a high damping is observed especially in the valley (see red dashed circle). Despite the relatively complex formula of equation 2 as compared to equation 1, figure 4c presents sharper features than those in figure 4b. In fact, the force gradient image, which is a local derivative, is more sensitive to noise than the oscillation phase and amplitude used in the energy loss image. On the other hand, figure 4c demonstrates that we could obtain energy loss maps with very high lateral resolution. Thus, by using the energy loss signal, quantitative magnetic data is derived with the same resolution as the phase images38,45 without detrimental effects of mathematical calculations. In figures 4d–f higher magnification images are presented to highlight morphological and magnetic features of the NPs film. In figure 4d, the aggregation of round magnetic NPs into elongated structures lying on the film top is shown. The aggregates clearly exhibit an internal structure of single magnetic NPs aligned into linear chains. The force gradient (figure 4e) shows the inner structure of the magnetic field within each aggregate (white markers in figures 4d–f), exhibiting different values within the same features, due to the inner magnetization distribution. In particular, each aggregate appears as half-bright and half-dark, resembling a typical contrast of magnetic dipoles34 even in absence of external magnetic field. This reveals the existence of a magnetic order46 within each chain at RT, resulting after dipole-dipole NPs interaction.

In the force gradient image (figure 4e) the independency of magnetic contrast from the topography is also clear, similar to figure 4b. The same conclusion applies for the energy loss image (figure 4f), in which the outer shape of the elongated NPs structures is nicely reproduced (as in figure 4c), showing a uniform dissipative coupling within each NPs chain. In this case a more fine-grained texture is observed as compared to figures 4b and 4e. The NPs could be resolved by reducing H to values that involve also non-magnetic tip-sample interactions, as reported in the supplementary information (figure S1.b). For both force gradient and energy loss a good signal–to–noise ratio is found (consistent with theoretical expectations shown in figures 2a and 2b), demonstrating that these signals are robust also for long–range forces in NAP mode.

Magnetic nanocomposite

In figure 5 MFM data (figure 5b–d) from slices of the nanocomposite is shown. The samples are prepared under an external magnetic field, to induce particle assembly as shown in the bright field TEM image (figure 5a), which helps in the correct interpretation of the contrast in the corresponding regions of MFM images (red dashed square in figures 5b–d). In particular, the dark regions of figure 5a correspond to the wire like structures of magnetic NPs, which appear dark in the TEM image with respect to the polymer matrix. Figure 5b shows the MFM topography, where NPs-rich regions protrude out of the matrix. Figures 5c and 5d show the force gradient and energy loss images, respectively.

Figure 5. Magnetic particle stripes inside the polymer matrix, examined with (a) TEM and (b) AFM.

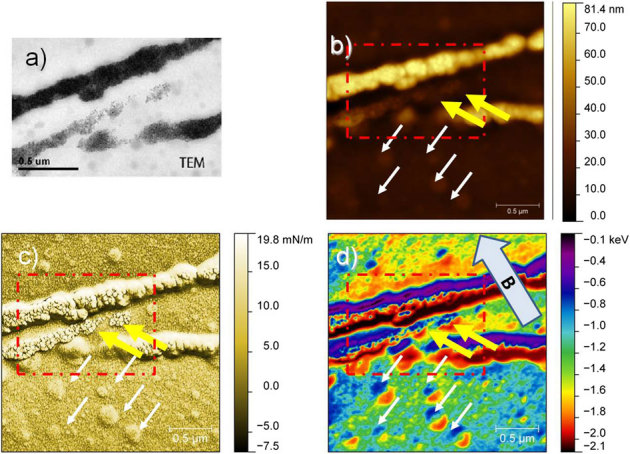
Figure 5

Open in a new tab

(c) and (d) represent the force gradient and the energy loss images. The red dashed square in b-d corresponds to TEM image. The yellow arrows indicate bare magnetic structures at the surface, exposed by the ultramicrotome cut and magnetic structures embedded in the polymer, both hardly visible in surface topography, but clearly revealed by the TEM measurement.

The observed ordering of NP assemblies into linear chains of few hundred nanometers width and some microns length (hereafter ‘nanowires’), is due to application of the magnetic field during sample preparation. This gives rise to a cooperative effect of the single crystal magnetic particles that undergo orientation along the easy axis, resulting into a long-range ordering that minimizes their dipole-dipole interaction energy13. The nanowires have SP behavior at RT20, therefore an external magnetic field is used to enhance magnetic contrast at the border of the stripes. In our case a weak (20 gauss) in-plane magnetic field, directed as the blue arrow in figure 5d, was adopted, causing an orientation of magnetic dipoles orthogonal to the stripes axis.

Discussion

Regarding the enhanced sensitivity following the correction factor γ(β) in figure 2c, this can theoretically reach a three-fold improvement for β∼10. However, there are practical limitations in the selection of the working parameters. First, when working in air a large free amplitude is required (A0∼100 nm in our case) to avoid tip sticking to the surface due to ambient humidity. Furthermore, to prevent tapping during the NAP pass it should be H>A0–ASP2. Ideally, for very small NPs and very sharp tips, e.g. dm∼dt∼10 nm, and with a molecular non-magnetic layer as thin as d0≤2 nm, it can be z0«H. Therefore, β∼H/ASP∼H/A0, and for β∼10 one would need an elevation H∼10 A0. In fact, the normal operating conditions for β lie on the left side of the maximum in γ(β), with β≤10. If, for example, a target sensitivity increase of γ = 2 is assumed, β should be ∼3. Furthermore, in our conditions dm = 11 nm but dt = 45 nm (with d0∼1.5 nm), therefore it is z0∼52 nm, not much smaller than H but rather approximately one half of it. In these conditions β∼1.5 H/ASP∼2 H/A0, which for an A0∼100 nm requires in turn H∼50 nm, which is a reasonable elevation for sensing magnetic forces. Actually, by proper tuning the working parameters a γ∼2.5 can be reached. For most commercial cantilevers the more common working conditions for β are indicated with a blue square in figures 2c and 2d.

For the bare NPs sample, the scale bars in figure 4 being expressed in physical units, allows for a direct comparison of the force gradient and energy loss images derived from AFM measurements (equations 1 and 2) with those theoretically calculated in the case of individual tip-particle interaction (equations 4 and 7, respectively), as previously described and indicated in figures 2a and 2b for the same working conditions. Due to compositional uniformity, long-range van der Waals forces are expected to give a uniform force gradient across the whole sample, affecting only the mean value of the signal, whereas local fluctuations are attributed to the magnetic texture of the sample, resulting in the contrast shown in figures 4b, c, e and f. The extent of the magnetic signal is, therefore, derived from the total amount of the fluctuation amplitude around the mean value of figure 4b, obtaining a peak to valley value of dF/dz≈375 μN/m. Similarly, the contrast in energy loss images, EL≈15 eV, is attributed to magnetic structures, while the mean value is regarded as a mainly compositional signal. A direct comparison between experimental results and theoretical predictions in case of single particle is reported in Table 1, allowing for a direct estimation of the number of particles involved in the tip-sample interaction processes. It is found that the interaction volume that contributes to energy dissipation signal corresponds to 100 particles, while a much smaller one, approx 8 particles, originates the force gradient signal. For these reasons a much higher magnetic volume is probed by energy loss imaging, as shown in figures 4c and 4f, while, the force gradient signal (figures 4b and 4e) involves a much smaller magnetic volume, and therefore is more sensitive to the first few layers on the surface, as previously discussed, consistently with different power low dependence of equations 4 and 8 on distance H.

Table 1. Comparison between measured tip-sample Interaction values in case of pristine nanoparticle samples, as shown in figure 4, and single particle expectation values as theoretically derived from equations 4 and 7. For the single particle calculations the experimental tip-sample parameters have been used (mm = 3*10−19 Am2; mt = 1*10−16 Am2; H = 20 nm; ASP = 85 nm; z0≈52 nm). The third column contains the ratio between experimental data and single particle expectation values, allowing for a direct estimation of the number of particles involved in the interaction.

Signal Measured Value (from figure 4b,c) Single particle expectation value Ratio (particles)
Force gradient 375 μN/m 48 μN/m ∼8
Energy loss 15 eV 150 meV ∼100
Open in a new tab

For the nanocomposite sample, the effect of the NPs-rich regions protruding out of the matrix (figure 5b) is probably following from a different surface relaxation after ultramicrotome cut, due to compositional non–uniformity in the solid film. The contrast observed in figure 5 is in agreement with the existing literature19,20,21. In particular, in the force gradient image of figure 5c a fine grained structure of the single magnetic NPs is detected throughout the magnetic stripes, which is not visible in the energy loss image of figure 5d. Additionally, in figure 5 some round NP aggregates of few hundred nanometers can be clearly distinguished (see yellow thick arrows), which in figure 5b do not exhibit a topographical contrast as strong as the elevated stripes. These features have a direct correspondence in figure 5a, where NPs aggregates are shown. Therefore, we conclude that both force gradient and energy loss are sensitive to magnetic interactions, as they were able to detect the magnetic particle assembly lying under the surface. Similar contrast is found in different parts of the imaged area, as pointed out by the white arrows in figures 5b–d.

In conclusion, we performed MFM measurements of∼11 nm diameter magnetic iron oxide NPs. When films of bare NPs deposited on a substrate were imaged, we detected linear magnetic chains of assembled NPs, with length of few hundred nanometers. Each assembly is a magnetic domain, likely due to particle aggregation during solvent evaporation. A superimposed magnetic fluctuation with hundred nanometers correlation length was also detected, interpreted as a dipole-dipole interaction between the NPs magnetic moments. When elongated NP assemblies forming SP nanowires embedded in a polymeric matrix were studied, our technique pointed out magnetic features as small as few tens of nanometers lying under the surface, which could not be detected by topographical imaging alone. Overall, we demonstrated the capability of MFM at RT in air to quantitatively characterize magnetic textures down to single particle level.

Methods

Nanoparticle synthesis

Nearly spherical mixed-phase γ-Fe2O3/Fe3O4 colloidal NPs with oleic acid (OLAC) as principal capping molecule were synthesized as described elsewhere19,20. The resulting hydrophobic NPs are soluble in non-polar solvents and have a diameter of (10.9±1.7) nm. Magnetic moment for individual particle (mm = 3*10−19 Am2) is calculated for 11 nm particle diameter as previously described13.

Nanoparticle films

A colloidal dispersion of NPs in toluene has been prepared. An aliquot of the solution was drop-casted onto substrates of freshly cleaved highly oriented pyrolitic graphite (HOPG, NT-MDT, ZYA grade), and let to dry in solvent saturated atmosphere at RT. The thickness of the formed films was (500±200) nm, as evaluated by the MFM topography, measured across holes and islands in the non-continuous NPs films.

Nanocomposite samples

A nanocomposite solution of 1 wt.% of γ-Fe2O3/Fe3O4 in poly(ethylmethacrylate-co-methylacrylate) (PEMMA, MW,100000 g/mole, Sigma-Aldrich) was prepared in chloroform. After sonicating for 10 minutes to avoid aggregation, the solution was drop-casted onto glass under a homogeneous magnetic field produced by two permanent magnets, applied parallel to the substrate. The magnetic field (B∼160 mT) drives the NPs movement parallel to the magnetic lines in the casted solution, during solvent evaporation. Formation of aligned SP nanowires, with 200 nm mean diameter and up to 15 nm length, uniformly dispersed in the whole polymer matrix, occurred, as previously reported19,20, which was also confirmed by SQUID magnetometry. The film thickness was ∼500 μm, as observed by optical microscopy of a cross section. Slices of 200 nm thickness were prepared, by cutting the nanocomposite approximately along the stripes with a EM UC6 ultramicrotome (Leica). The slices were laid onto 50 nm thick Si3N4 TEM membranes (4124SN-BA, SPI Supplies) in order to perform TEM and MFM measurements. Top camera is used to locate the tip in the center of the 500 μm×500 μm membrane while data is collected by progressively reducing AFM scan size from 50 μm×50 μm to few micrometers to obtain the desired resolution on the features. The same procedure is then followed during TEM measurements to directly identify the same features in the sample.

Electron microscopy

Images of the bare magnetic NPs were acquired via TEM and STEM performed with a JEOL JEM-2200FS operating at 200 kV and equipped with an energy filter (Omega type). Filtered elastic images were acquired to verify the presence of OLAC capping layer on the particles. Images of nanocomposite samples were acquired via TEM performed with a JEOL JEM-1011 microscope operating at 100 kV in bright-field mode.

MFM operation

For all the experiments, commercial rectangular silicon cantilever coated with a CrCo layer of ∼45 nm thickness have been used (Asylum Research MFM standard, coercitivity ∼400 Oe, magnetization ∼10−13 emu). The nominal spring constant k and resonance frequency ν0 were 2.5 N/m and 75 kHz, respectively. For each measurement the k and the free oscillation amplitude A0 have been calibrated on a non-magnetic rigid sample. A standard two-pass technique (NAP mode in our instrument) has been adopted. At each scan line, the topography is first acquired (with an amplitude setpoint ASP1, usually a 60% to 80% fraction of the free oscillation amplitude A0) and then the scan is repeated on the same line with an offset elevation H0 (NAP height) set to a higher value than Ao–ASP1. In this way topography cross-talk with the magnetic interaction is prevented, and the cantilever oscillation parameters during the second pass are used to build up maps of the long-range interactions. At each location, measurements are repeated twice to independently collect amplitude and phase (at constant frequency, in amplitude modulation mode) and frequency shift. Frequency shift is automatically detected by using the phase shift as error signal for the feedback loop, used to track the variation of the resonance frequency by changing the dither frequency by means of the microscope controller. Phase is previously nulled in correspondence of the maximum of the first free resonance peak to compensate spurious phase shifts due to the setup, while microscope parameters such as feedback loop gain and scanning speed are, optimized to keep the phase signal to zero during second pass. During both the topographic tracking (first) pass and the elevated NAP (second) pass, the cantilever was dithered in high oscillation amplitude regime (A0>50 nm) to prevent tip sticking to the particles capping layer by means of the high elastic force. Due to both the long distance from the magnetic features and the tip blunting resulting from its magnetic coating, the lateral resolution is significantly decreased with respect to standard AFM. Since the typical radius of curvature of commercial MFM probes lies in the range of 20–100 nm, a comparable lateral resolution is expected.

For the nanocomposite sample, the MFM measurement has been carried out under a weak (20 gauss) external magnetic field with in-plane orientation perpendicular to the stripes, to highlight magnetic texture in the sample.

Author Contributions

BT and AA conceived of the study and participated in its design. DF prepared all nanocomposite samples, GB prepared the nanocomposites slices at the ultramicrotome and performed the TEM measurements. BT developed the theoretical part on MFM, carefully revised by AF, MS and GB. BT performed MFM measurements and their interpretation in terms of the MFM theoretical part previously discussed, as shown in the “Results” and in the “Discussion” sections, after basilar discussion with MS, AF, and GB. BT and MS drafted the manuscript, substantially revised by AA, RC, AD and DF. All authors read and approved the final manuscript.

Supplementary Material

Supplementary Information

Supplementary Information

srep00202-s1.doc (2MB, doc)

Acknowledgments

The authors thank Dr. P. D. Cozzoli of National Nanotechnology Laboratory (NNL), CNR-Istituto di Nanoscienze, Università del Salento, for providing the iron oxide nanoparticles used in this work.

References

  1. Papaefthymiou G. C. Nanoparticle magnetism. Nano Today 4, 438–447 (2009). [Google Scholar]
  2. Sun S. Self-Assembled FePt Nanoparticle Arrays as Potential High-Density Recording Media. Magnetic nanostructures 208 (2007). [Google Scholar]
  3. Millan A. et al. Maghemite polymer nanocomposites with modulated magnetic properties. Acta Materialia 55, 2201–2209 (2007). [Google Scholar]
  4. Bertoni G. et al. Growth of multi-wall and single-wall carbon nanotubes with in situ high vacuum catalyst deposition. Carbon 42, 440–443 (2004). [Google Scholar]
  5. Arruebo M., Fernández-pacheco R., Ibarra M. R. & Santamaría J. Magnetic nanoparticles Controlled release of drugs from nanostructured functional materials. Review Literature And Arts Of The Americas 2, 22–32 (2007). [Google Scholar]
  6. Nedkov I. et al. Size effects in monodomain magnetite based ferrofluids. Journal of Nanoparticle Research 10, 877–880 (2007). [Google Scholar]
  7. Miltenyi S., Müller W., Weichel W. & Radbruch A. High gradient magnetic cell separation with MACS. Cytometry 11, 231–238 (1990). [DOI] [PubMed] [Google Scholar]
  8. Mørup S., Hansen M. F. & Frandsen C. Comprehensive Nanoscience and Technology. (Elsevier: 2011).10.1016/B978-0-12-374396-1.00036-2. [Google Scholar]
  9. Berger P. et al. Preparation and Properties of an Aqueous Ferrofluid. Journal of Chemical Education 76, 943 (1999). [Google Scholar]
  10. Godovsky D. Biopolymers · PVA Hydrogels, Anionic Polymerisation Nanocomposites. 153, 163–205 (Springer-Verlag: Berlin, Heidelberg 2000). [Google Scholar]
  11. Carzino R. et al. Patent. WO 2011/121519 (2011). [Google Scholar]
  12. Bonacchi D. et al. Nanosized Iron Oxide Particles Entrapped in Pseudo-Single Crystals of γ-Cyclodextrin. Chemistry of Materials 16, 2016–2020 (2004). [Google Scholar]
  13. Bertoni G. et al. Nanochains Formation of Superparamagnetic Nanoparticles. The Journal of Physical Chemistry C 115, 7249–7254 (2011). [Google Scholar]
  14. Rugar D. et al. Magnetic force microscopy: General principles and application to longitudinal recording media. Journal of Applied Physics 68, 1169 (1990). [Google Scholar]
  15. Proksch R. B. et al. Magnetic force microscopy of the submicron magnetic assembly in a magnetotactic bacterium. Applied Physics Letters 66, 2582 (1995). [Google Scholar]
  16. Kleiber M. et al. Magnetization switching of submicrometer Co dots induced by a magnetic force microscope tip. Physical Review B 58, 5563–5567 (1998). [Google Scholar]
  17. Brown W. Thermal Fluctuations of a Single-Domain Particle. Physical Review 130, 1677–1686 (1963). [Google Scholar]
  18. Tannous C. & Gieraltowski J. The Stoner–Wohlfarth model of ferromagnetism. European Journal of Physics 29, 475–487 (2008). [Google Scholar]
  19. Fragouli D. et al. Dynamical formation of spatially localized arrays of aligned nanowires in plastic films with magnetic anisotropy. ACS nano 4, 1873–1878 (2010). [DOI] [PubMed] [Google Scholar]
  20. Fragouli D. et al. Formation and microscopic investigation of iron oxide aligned nanowires into polymeric nanocomposite films. Microscopy research and technique 73, 952–958 (2010). [DOI] [PubMed] [Google Scholar]
  21. Ando T., Hirota N. & Wada H. Numerical simulation of chainlike cluster movement of feeble magnetic particles by induced magnetic dipole moment under high magnetic fields. Science and Technology of Advanced Materials 10, 014609 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Aoshima M. & Satoh A. Two-dimensional Monte Carlo simulations of a colloidal dispersion composed of polydisperse ferromagnetic particles in an applied magnetic field. Journal of colloid and interface science 288, 475–488 (2005). [DOI] [PubMed] [Google Scholar]
  23. Aoshima M. & Satoh A. Two-dimensional Monte Carlo simulations of a polydisperse colloidal dispersion composed of ferromagnetic particles for the case of no external magnetic field. Journal of colloid and interface science 280, 83–90 (2004). [DOI] [PubMed] [Google Scholar]
  24. Fiorani D., Testa a. M., Lucari F., D’Orazio F. & Romero H. Magnetic properties of maghemite nanoparticle systems: surface anisotropy and interparticle interaction effects. Physica B: Condensed Matter 320, 122–126 (2002). [Google Scholar]
  25. Raşa M., Kuipers B. W. M. & Philipse a. P. Atomic force microscopy and magnetic force microscopy study of model colloids. Journal of colloid and interface science 250, 303–315 (2002). [DOI] [PubMed] [Google Scholar]
  26. Schreiber S. et al. Magnetic force microscopy of superparamagnetic nanoparticles. Small 4, 270–278 (2008). [DOI] [PubMed] [Google Scholar]
  27. Neves C. S. et al. New insights into the use of magnetic force microscopy to discriminate between magnetic and nonmagnetic nanoparticles. Nanotechnology 21, 305706 (2010). [DOI] [PubMed] [Google Scholar]
  28. Dietz C., Herruzo E. T., Lozano J. R. & Garcia R. Nanomechanical coupling enables detection and imaging of 5 nm superparamagnetic particles in liquid. Nanotechnology 22, 125708 (2011). [DOI] [PubMed] [Google Scholar]
  29. Lozano J. & Garcia R. Theory of Multifrequency Atomic Force Microscopy. Physical Review Letters 100, 8–11 (2008). [DOI] [PubMed] [Google Scholar]
  30. Xu X., Melcher J., Basak S., Reifenberger R. & Raman A. Compositional Contrast of Biological Materials in Liquids Using the Momentary Excitation of Higher Eigenmodes in Dynamic Atomic Force Microscopy. Physical Review Letters 102, 13–16 (2009). [DOI] [PubMed] [Google Scholar]
  31. Hu S. & Raman A. Chaos in Atomic Force Microscopy. Physical Review Letters 96, 1–4 (2006). [DOI] [PubMed] [Google Scholar]
  32. Hu S. & Raman A. Analytical formulas and scaling laws for peak interaction forces in dynamic atomic force microscopy. Applied Physics Letters 91, 123106 (2007). [Google Scholar]
  33. Varón M. et al. Dipolar driven spontaneous self assembly of superparamagnetic Co nanoparticles into micrometric rice-grain like structures. Langmuir: the ACS journal of surfaces and colloids 26, 109–116 (2010). [DOI] [PubMed] [Google Scholar]
  34. Mironov V. L., Nikitushkin D. S., Petrov D. S., Shubin a. B. & Zhdan P. a Simulation of the MFM contrast from small low-coercive ferromagnetic nanoparticles in an external field. Journal of Surface Investigation. X-ray, Synchrotron and Neutron Techniques 1, 348–351 (2007). [Google Scholar]
  35. Mironov V. L., Nikitushkin D. S., Bins C., Shubin A. B. & Zhdan P. a Magnetic Force Microscope Contrast Simulation for Low-Coercive Ferromagnetic and Superparamagnetic Nanoparticles in an External Magnetic Field. IEEE Transactions on Magnetics 43, 3961–3963 (2007). [Google Scholar]
  36. Vergara J., Eames P., Merton C., Madurga V. & Dahlberg E. D. Moment determination of magnetic force microscope tips by imaging superparamagnetic films. Applied Physics Letters 84, 1156 (2004). [Google Scholar]
  37. Jesse S., Kalinin S. V., Proksch R., Baddorf a. P. & Rodriguez B. J. The band excitation method in scanning probe microscopy for rapid mapping of energy dissipation on the nanoscale. Nanotechnology 18, 435503 (2007). [Google Scholar]
  38. Martínez N. F. & García R. Measuring phase shifts and energy dissipation with amplitude modulation atomic force microscopy. Nanotechnology 17, S167–S172 (2006). [DOI] [PubMed] [Google Scholar]
  39. García R., Magerle R. & Perez R. Nanoscale compositional mapping with gentle forces. Nature materials 6, 405–411 (2007). [DOI] [PubMed] [Google Scholar]
  40. Garcia R. et al. Identification of Nanoscale Dissipation Processes by Dynamic Atomic Force Microscopy. Physical Review Letters 97, 1–4 (2006). [DOI] [PubMed] [Google Scholar]
  41. Fernández-López C. et al. Highly Controlled Silica Coating of PEG-Capped Metal Nanoparticles and Preparation of SERS-Encoded Particles (dagger). Langmuir: the ACS journal of surfaces and colloids 25, 13894–13899 (2009). [DOI] [PubMed] [Google Scholar]
  42. Albrecht T. R., Grutter P., Horne D. & Rugar D. Frequency modulation detection using high-Q cantilevers for enhanced force microscope sensitivity. Journal of Applied Physics 69, 668 (1991). [Google Scholar]
  43. Canale C., Torre B., Ricci D. & Braga P. C. Recognizing and Avoiding Artifacts in Atomic Force Microscopy Imaging. Methods in molecular biology (Clifton, N.J.) 736, 31–43 (2011). [DOI] [PubMed] [Google Scholar]
  44. Koch S. Magnetic force microscopy on cobalt nanocluster films. Applied Surface Science 226, 185–190 (2004). [Google Scholar]
  45. Tamayo J. & Garcia R. Relationship between phase shift and energy dissipation in tapping-mode scanning force microscopy. Applied Physics Letters 73, 2926–2928 (1998). [Google Scholar]
  46. Pei W., Kumada H., Natusme T., Saito H. & Ishio S. Study on magnetite nanoparticles synthesized by chemical method. Journal of Magnetism and Magnetic Materials 310, 2375–2377 (2007). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep00202-s1.doc (2MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES