Abstract
A possible functional role of finger representations for the development of early numerical cognition has been the subject of recent debate; however, until now, only behavioral studies have directly supported this view. Working from recent models of number processing, we focused on the neural networks involved in numerical tasks and their relationship to the areas underlying finger representations and saccades in children aged 6–12 years. We were able to differentiate three parietal circuits that were related to distinct aspects of number processing. Abstract magnitude processing was subserved by an association area also activated by saccades and visually guided finger movements. Addition processes led to activation in an area only engaged during saccade encoding, whereas counting processes resulted in the activation of an area only activated during visually guided finger movements, namely in the anterior intraparietal sulcus. Apart from this area, a large network of specifically finger-related brain areas including the ventral precentral sulcus, supplementary motor area, dorso-lateral prefrontal cortex, insula, thalamus, midbrain, and cerebellum was activated during (particularly non-symbolic) exact addition but not during magnitude comparison. Moreover, a finger-related activation cluster in the right ventral precentral sulcus was only present during non-symbolic addition and magnitude comparison, but not during symbolic number processing tasks. We conclude that finger counting may critically mediate the step from non-symbolic to symbolic and exact number processing via somatosensory integration processes and therefore represents an important example of embodied cognition.
Keywords: canonical numerical hand shapes, movement vocabulary, ordinal aspects of cognition
Introduction
A possible role for fingers in numerical cognition
A possible functional role for finger representations in the development of numerical cognition has recently been debated (e.g., Andres et al., 2008). This discussion has received support from different studies in both children and adults. Recent findings in children included the following: that finger gnosis was a better predictor than was global development for calculation skills 1 year later but not for reading (Noël, 2005); that a pure finger gnosis training improved some numerical skills (Gracia-Bafalluy and Noël, 2008); and that finger-related split-five-errors occurred in a high percentage of primary school children, especially when they were starting to retrieve the results of simple addition and subtraction as arithmetical facts from long-term memory (Domahs et al., 2008). In adults, it has been shown that directional finger counting habits have an effect on individual cognitive spatial–numerical associations (Di Luca et al., 2006; Fischer, 2008; Sato and Lalain, 2008; but see Brozzoli et al., 2008, for contrasting results) and that even in adults, finger counting-related sub-base-5 representations have an impact in Arabic number magnitude comparisons (Domahs et al., 2010).
This functional relationship between finger counting and numerical representations might be related to the anatomical proximity of relevant brain areas (for a recent review, see Dehaene, 2009). Thus far, the only imaging study investigating numerical processing using pictures of canonical hand shapes for numbers (Kaufmann et al., 2008) has revealed respective activations in the bilateral supramarginal gyrus and anterior intraparietal sulcus (aIPS) extending to the post- and precentral gyrus; these activations were stronger in children than in adults.
From a cognitive point of view, canonical finger configurations as used for showing numbers might serve as iconic representations of numerosities (Fayol and Seron, 2005). It has been shown that, at least in adults, canonical hand shapes for numbers automatically activate exact number semantics, whereas non-canonical ones do not (Di Luca and Pesenti, 2008). Furthermore, canonical hand shapes for numbers are cognitively processed similar to number symbols, whereas non-canonical hand shapes are processed like non-symbolic magnitudes (Di Luca et al., 2010). This pattern of findings points to a possible role of number-related finger configurations as a “missing link” (Fayol and Seron, 2005) or “missing tool” (Andres et al., 2008) for connecting non-symbolic numerosities and symbolic number representations as needed for arithmetic. However, it remains unknown to what extent the symbolic processing of numerical canonical hand shapes is present in children, and if so, whether it becomes more or less relevant during development.
Embodied cognition
It has been suggested that finger counting is a prototypical example for embodied cognition (Wilson, 2002; see also Fischer and Brugger, 2011). Children learn the ordinal aspects of number processing by (finger) counting (Brannon and Van de Walle, 2001). This process requires somatosensory integration, a process that may play a major role in cognitive development (Piaget, 1952) and may be paralleled by an integrated involvement of parietal and frontal brain areas. The theory of embodied cognition similarly postulates that mental concepts may be built up out of cognitive primitives that are, themselves, somatosensory in nature (Wilson, 2002) or are at least influenced by bodily constraints (Anderson, 2003), such as the fact that we have five fingers on each hand (Domahs et al., 2010). The neural mechanism that has been suggested to underlie all forms of embodied cognition is the repeated firing of similar neural populations in a similar pattern (see Niedenthal et al., 2005, for a review).
In any case, trying to understand the functional role of finger-related brain areas for numerical cognition requires knowledge about the neural correlates for finger representations. This topic will be explored in the next section.
Brain regions associated with finger representation
The brain systems engaged in the sensory- and motor-related aspects of the fingers are distinct in nature and are organized along the ascending and descending pathways of the brain. The somatotopic organization of the brain related to the fingers is found along the pathways from the fingers themselves up to the higher representations in the motor cortex. They include systems in the spinal cord, medulla, ventral basal complex, S1, S2 (insula), anterior and posterior parietal lobule, anterior IPS, and SMA. In general, the somatotopic organization in the motor cortex is substantially less precise than in the sensory cortex (FitzGerald, 1985).
The premotor and motor cortex areas code for the directions of movements and are hierarchical in their organization. Actual movement execution is organized by lower motor systems in the peripheral nervous system; yet, the cerebral motor cortex is tightly interconnected with the basal ganglia and the thalamus, from which it receives input via a feedback loop (FitzGerald, 1985). Abstract motor programs (as needed for finger counting) are believed to also include the activation of the pre-supplementary motor area (preSMA), the SMA proper, the frontal eye fields (FEF), and the IPS (FitzGerald, 1985). In addition, the frontal operculum (FOP) may be engaged in the linking of verbal labels to sequences because it is active in both verbal as well as in imagined movements of the tongue and hand (Schubotz and von Cramon, 2001).
In a review paper, Rizzolatti and Lupino (2001) explained that in the primate motor cortical areas, at least three types of higher cognitive functions are already subserved: somatosensory transformations, action understanding, and decision processing regarding action execution. Specifically, the primate brain area F5, which is located in the ventral premotor cortex (vPMC) and receives the most input from the anterior intraparietal (AIP) region (see also Koten et al., 2009 for the genetic functional connectivity of these two areas in humans) is thought to underlie the organization of hand and mouth movements by coding for specific actions (and not the single movements that form them) in the sense of a “motor vocabulary” (Rizzolatti and Lupino, 2001). More specifically, in humans, the vPMC and the intraparietal areas (among other areas including the inferior frontal gyrus) have been shown to be related to finger sequence complexity (Harrington et al., 2000; Haslinger et al., 2002) and to encoding interval (and ordinal) aspects of visually presented sequences (Schubotz and von Cramon, 2001). Furthermore, the vPMC and the anterior part of the IPS have been found to be active during the observation of actions, with an interesting lateralization of the vPMC activation that was stronger on the left side for watching actions with wrong objects and stronger on the right side for wrong movements (Manthey et al., 2003). Two reviews have pointed to similar roles of the vPMC, namely for task representations (Brass et al., 2005) and for higher aspects of goal-directed (finger) actions in humans (Binkofski et al., 1999). Taken together, the vPMC and anterior parietal cortex seem to subserve higher cognitive aspects of hand motor sequences and action encoding and may, therefore, be optimal candidates for the neural correlates of finger counting-related embodied cognition in number processing. The next section will focus on the possible additional role of these cortical areas in numerical cognition.
Brain regions for number representation
Non-human primate studies and studies in other mammal species suggest that there are three classes of number neurons in the intraparietal sulcus in different areas that may be linked to distinct forms of number processing (see also Dehaene, 2009). First, the accumulation of visually presented objects might rely on the neural systems located in the lateral intraparietal area (LIP) in the monkey, systems which might also be related to the memory for saccadic positions (Roitman et al., 2007). In humans, it has been shown that the neural circuitry involved in eye movements seems to be differentially recruited for mental arithmetic: addition seems to activate neurons subserving rightward saccades, whereas subtraction shows a relatively stronger activation of neurons subserving leftward saccades (Knops et al., 2009). The LIP area is located in the lateral aspects of the monkey brain, but the human homolog of this area remains a matter of debate (Shikata et al., 2008). A recent study found such accumulating number-sensitive neurons in the human posterior superior parietal lobe (PSPL: Santens et al., 2010). Second, counting behavior might rely on number neurons that code for action in the AIP area, which is closely linked to representations of the hand (monkey brain: Sawamura et al., 2002). This area corresponds to the aIPS/postcentral sulcus in humans, which was found to be active in children in a numerical task using hand pictures as stimuli (Kaufmann et al., 2008). Third, abstract representations of numbers are assumed to be linked to multi- or polymodal brain systems such as the ventral intraparietal area (cat brain: VIP; Thompson et al., 1970), which processes number magnitude information independent of stimulus modality (human brain: Piazza et al., 2007).
Recently, Bongard and Nieder (2010) suggested that successful rule applications, as needed for arithmetic operations, might depend on prefrontal cortex (PFC) areas in monkeys. In humans, both intraparietal and dorso-lateral prefrontal (DLPF) areas, among others, were shown to be active during number processing and calculation (see Arsalidou and Taylor, 2011 for a recent meta-analysis). The (bilateral) vPMC was also among the brain areas identified in this meta-analysis, although its function in number processing was hardly discussed (but see Pesenti et al., 2000; Venkatraman et al., 2005 for exceptions relating this vPMC activation to finger counting in both adults and children, respectively). A recent study found that only the right vPMC showed overlapping activations during the numerical judgment of sequentially as well as simultaneously presented visual stimuli, which points to a role of the right vPMC in some kind of internal numerical representations (Dormal et al., 2010). A study using transcranial magnetic stimulation (TMS) confirmed the functional role of the vPMC in counting (Kansaku et al., 2007), and two studies have shown that number processing changed the motor excitability of the hand (Andres et al., 2007; Sato et al., 2007), thus adding strong evidence to the role of the vPMC for numerical processing. Furthermore, the first study investigating the use of pictures of hands with different numbers of raised fingers as numerical stimuli identified the postcentral sulcus extending into the aIPS as a possible key region for finger-based numerical representations (Kaufmann et al., 2008). A recent meta-analysis found that this region was more active in dyscalculic children than in typically developing children and was more active in the latter compared to adults. Neural activity in this key brain region was also increased in children during non-symbolic compared to symbolic number processing (Kaufmann et al., 2011). One may conclude that the acquired motor programs for finger counting (presumably subserved by the vPMC and aIPS) might still be active during (non-symbolic) number processing, even when children do not continue to use fingers for calculation, and also that the importance of finger areas might decrease with age.
Research questions
The findings from different fields of research as described above lead to the following assumptions:
If the ordinal aspects of number processing such as finger counting play a role for the development of numerical cognition due to the somatosensory integration of finger representations into number representations, brain areas related to the motor loop system for fingers such as the S1, aIPS, S2 (insula), vPMC, (pre)SMA, M1, FEF, thalamus, and basal ganglia may be active during number processing tasks in children. Of these areas, specifically, the aIPS/postcentral sulcus (somatosensory finger representations) and the vPMC (“motor vocabulary”) might be key candidate areas for finger-based number representations.
To ensure that the activation in our finger movement task (see Materials and Methods) was exclusively related to finger representation and not to other cognitive aspects such as vision or eye movement, we used the encoding phase of a visual working memory task as a control condition. This choice should enable us to differentiate different aspects (finger-related, saccade-related, polymodal) of numerical processing in intraparietal areas (see Dehaene, 2009 for a similar approach) with inclusion and exclusion analyses (see Materials and Methods). The latter is of importance because visually guided finger movements activate large parts of the brain that might completely overlap with number tasks and, therefore, show very little differentiation.
Specifically, we expect that polymodal (non-symbolic as well as symbolic) number representations should be found in the polymodal association cortex (VIP), which should also be active in both the finger movement and the saccade tasks. Furthermore, activation related to addition should be found in areas that are coactivated by visually guided saccades (LIP). Counting operations (as needed for the non-symbolic exact addition task) might go along with coactivation of the somatosensory and premotor cortex (AIP and vPMC).
In general, finger-related activations might be more active in addition than in magnitude comparison because finger counting is more frequently used and more important for calculation. However, at least in adults, cognitive traces of finger-based number representations have also been found for more basic tasks such as number comparison. Furthermore, finger-related activation should be more active during non-symbolic activation than during number processing because finger-based numerical representations might provide a link to exact magnitude representations, which can be directly accessed by number symbols. Finally, we expect a decrease of number-related activations in finger-related areas with age.
Materials and Methods
Participants
Overall, 33 school-aged children participated in our study. Among them, 10 children moved more than 3.5 mm during at least one of the functional tasks and were therefore excluded from the data analysis. Technical problems during functional data acquisition led to the exclusion of two more children; one child was only correct in approximately 50% of all trials of one task (non-symbolic addition) and thus was also excluded. Finally, the functional data of 20 children (9 girls) between 69 and 150 months of age (mean age: 108 months, SD: 21 months) were included in the study. Their estimated IQ (Colored Progressive Matrices; Bulheller and Häcker, 2002) ranged from the 32nd to the 100th percentile with a mean percentile of 66 (SD = 21). All children attended normal schooling, had normal or corrected to normal vision, and had no reported history of major medical illness, neurological, developmental, or psychiatric disorder (except for one child with known attention-deficit disorder). The study was approved by the local ethics committee and was conducted according to the Convention of Helsinki. Written and informed consent was obtained from all caregivers of the children. The children received a small financial compensation for participation.
Tasks and stimuli
The children were familiarized with all tasks outside the scanner on a computer screen. In the scanner, they started with a visually guided finger movement task, followed by four numerical tasks in pseudo-random order, and a visual working memory task (of which the encoding phase was used for this study) in the end. Between the tasks, the scanner was stopped, children were asked if everything was all right, told which task was to complete next, and, if necessary, reminded to lie still. It is important to note that the children could not use their fingers for counting in the scanner because they had to keep their right and left index fingers on the response buttons as a task requirement. Furthermore, the children were observed from outside the scanner to check whether they had removed their fingers from the response device placed over their stomachs; fortunately, no child did so during the study period.
During the visually guided finger movement task, children observed four horizontally aligned black dots (approximately 2 cm in diameter) against a white background that turned red in pseudo-randomized order. Each dot corresponded to a finger: the leftmost dot to the left middle finger, the next one to the left index finger, the third dot to the right index finger, and the rightmost dot to the right middle finger. The children were asked to press the correct button as soon as a corresponding dot turned red. In the scanner, an MR-compatible response box with four horizontally aligned response buttons was centrally placed on the participants. Stimuli were presented in 4 blocks of 12 stimuli each. Rest conditions were included for 14 s between the blocks. This task was used to elicit brain activations related to finger representations that are thought to be needed for finger counting as well, as in both instances the differentiation of specific fingers is necessary.
The four numerical tasks represented symbolic and non-symbolic magnitude comparison as well as symbolic and non-symbolic addition. In each task, two numerosities were presented simultaneously on the screen until the children pressed a button (left or right index finger) in response. In the scanner, an MR-compatible response box with four response buttons was centrally placed on the participants, and responses were given by pressing the leftmost or the rightmost button, respectively. In a recently published pilot study, we showed that this self-paced stimulus presentation paradigm was much more reliable and was at least as sensitive as a fixed stimulus presentation paradigm (Krinzinger et al., 2011). In the magnitude comparison tasks, children had to press the button corresponding to the side with the larger stimulus, and a vertical white line was always present in the middle of the black screen and also in the rest condition. In total, 24 stimuli were presented in two blocks of 12 stimuli each, with a rest condition of 14 s after each block. In the addition task, children had to press the right button if the two numerosities added up to 7 and the left button if the respective result was smaller or larger than 7. A white plus sign was always present during the addition tasks. The presented numerosities ranged from 2 to 5 (identical numerosities were never presented within one item so that the same stimuli could be used for the magnitude comparison and the addition tasks). The 24 addition stimuli were presented in 6 blocks comprising 4 stimuli each. The rest condition was again 14 s between blocks. The 24 stimulus combinations employed in each task were designed such that half of them added up to 7, the other half added up equally often to a number smaller (5 or 6) or larger (8 or 9) than 7, and the larger numerosity was presented on the left side and the right side equally often. In the non-symbolic tasks, two dot arrays (black randomly distributed dots in a white circle against a black background) were used as stimuli. These dot arrays were created using a Matlab program available on www.unicog.org). In half of the pairs, dots of both arrays had the same size, and in the other half, the overall area of dots was equal (see Figure 1 for an example stimulus of exact non-symbolic addition with equal overall area of dot arrays). For the symbolic tasks, Arabic digits were presented in white and appeared approximately as large as the dot patterns on the screen (approximately 9 cm).
Figure 1.
Example stimulus of the exact non-symbolic addition task with equal overall area of dots for both arrays.
During the visual working memory task, the children observed three randomly distributed large dots which turned blue for 1 s, one after the other, a fixation cross for 3 s, and then the same three dots which turned blue in either the same or a different order. They then had to decide whether the sequence was the same (right button press) or not the same (left button press). This task was repeated with 24 differently shaped stimuli, with rest periods for 14 s after sets of 4 stimuli each. In the scanner, an MR-compatible response box with four response buttons was centrally placed on the participants, and responses were given by pressing the leftmost or the rightmost button, respectively. Only activation data from the encoding phase (visually guided saccades) was used for this study. It is important to note that no finger movements were required during this encoding phase.
Stimulus presentation and data recording were accomplished using Presentation (Neurobehavioral Systems, Albany, CA, USA)1. In the MR scanner, participants viewed the stimuli via MRI-compatible video goggles (VisuaStim XGA, Resonance Technology) with a horizontal viewing angle of 30° and a vertical viewing angle of 22.5°.
MRI image acquisition
Imaging was performed on a 3-T magnetic resonance scanner (Siemens Trio, Siemens Medical Systems, Erlangen, Germany) using a 16-channel head coil. To minimize head movement, children’s heads were comfortably stabilized with foam cushions. Previous child studies showed partly disappointing results with conventional sequences. Here, we applied a parallel imaging technique that allows for relatively fast acquisition times at the cost of reduced signal to noise ratio. The benefit of this method is that data are less prone to spatial distortions, and corrections for head movements can be applied with greater precision compared to normal sequences with relatively slow TR times. Functional images were obtained using an echo-planar image (EPI) 2D bold Grappa sequence with an acceleration factor of 2 sensitive to blood oxygen level-dependent (BOLD) contrast with the following parameters: repetition time (TR) = 1.600 ms, echo time (TE) = 30 ms, flip angle (FA) = 72°, field of view (FOV) = 384 × 384, slice thickness (ST) = 3.5 mm with 10% gap, matrix size (MS) = 64 × 64, spatial resolution = 3.5 mm × 3.5 mm × 3.5 mm, and 30 axial slices parallel to the AC–PC line. A T1-weighted anatomical data set was obtained from each child (TR = 1.900 ms, TE = 2.52 ms, FA = 9°, FOV = 256 × 256, ST = 1 mm, spatial resolution 0.98 mm × 0.98 mm × 1 mm).
Functional imaging data preprocessing
The structural T1 scans of all children were brought into Talairach space (Talairach and Tournoux, 1988) using semi-automatic procedures. The co-registration file obtained during this step was used for all further co-registration purposes described below. The EPI sequences were processed with the following procedure: a slice scan time correction was executed using sinc interpolation. Subsequently, data were corrected for head movements using sinc interpolation, and 10 children with head movements larger than one voxel size (3.5 mm) were not included in the sample (see above). Next, linear trends were removed from the time courses using fast Fourier transformation methods, and a high pass filter was applied with two cycles. Subsequently, data were spatially smoothed with a smoothing kernel of 7 mm. The functional data were than co-registered with the anatomical scans in native space using sinc interpolation. This step was necessary for the creation of so-called volume time course maps (VTC). Finally, the time courses were aligned in Talairach space using the alignment files that were obtained in the previous steps and re-sampled on a 3-mm iso-voxel grid using sinc interpolation.
In addition, a child template in Talairach space was produced based on children’s brain scans obtained in another study (Krinzinger et al., 2011). Finally, this template was used for the projection of all significant brain activation maps. In contrast to this previous study, the data were not cortically aligned in the actual study. Therefore, our results do not have the precision and quality of cortex-based aligned studies, and conclusions about the exact localization of brain activation spots have to be interpreted with caution for two reasons. First, part of the spatial resolution of data is lost due to spatial smoothing. Second, transformations that do not rely on cortex-based alignment can be corrupted by large mismatches in spatial correspondences of individual anatomical structures (Ghosh et al., 2010). Nevertheless, a true child template in Talairach space is to be preferred over the usually applied adult template in Talairach space. Although the anatomical structures of higher cortical systems in the children’s brains will not likely correspond to the anatomical structures of an individual female adult brain (Talairach and Tournoux, 1988; Giedd et al., 1999), we will refer to the Talairach coordinates in this study, to make our results more comparable to previous (and future) findings.
Functional data analyses
From the VTC data, linear contrast beta weights were estimated at the first level, with the standard general linear model (GLM) as implemented in BVQX 2.32 using the separate subject option. Percent signal change normalization was applied such that the data from distinct runs can be compared for further statistical analysis. The variance caused by head movements was removed from the data with the head movement data as predictors of no interest in the GLM. Next, beta weight estimates for experimental design parameters corrected for head movements were imported into Matlab using BVQX tools3. Subsequently, the beta weights of the six tasks under study were analyzed at the second level for deviation from zero using t-tests. The maps resulting from the t-test were used for inclusion and exclusion analyses.
For the inclusion (or conjunction) analysis, the logic of Nichols et al. (2005) was followed. They based their approach on the minimum t-statistics, providing very conservative estimates for the conjunctions of brain activation data (Friston et al., 2005). All the areas of activation in our analyses arise from conjunction analyses obtained from a varying number of contrasts (two to six). Depending on the statistical philosophy in use, all conjunctions are either declared significant at p = 0.01 (Nichols et al., 2005) or conjunctions are significant in a p-value range between p = 0.012 and p = 0.016 (see for example the computation in Price and Ansari, 2011, p. 1207). In the exclusion (or disjunction) analyses (concerned with two sets of paradigms/contrasts), only those voxels are considered significantly activated, which are activated above a certain threshold in all “included” paradigms (see Nichols et al., 2005), but not in any of the “excluded” paradigms. This approach does not test for relative activation differences but does test for the presence or absence of activation in two (non-empty, non-overlapping) sets of contrasts.
The combined use of conjunction/disjunction analysis is less conventional, but it is similar to the “masked conjunction analysis” procedure introduced in 1997 (Price et al., 1997; see also Xu et al., 2001). Masking is a very conventional method within the SPM philosophy. In our study, conjunction/disjunction (or inclusion/exclusion) analyses have some advantages over direct contrasts for the following reasons: first, inclusion/exclusion analyses do not suffer from an artificial boost of activation differences, as observed in unmasked direct contrasts, in which areas of deactivation may be subtracted from areas of activation. Second, inclusion/exclusion analyses do not suffer from masking artifacts that might occur when direct contrasts are masked for deactivated areas. Third, inclusion/exclusion analyses can show higher test–retest reliability when compared to direct contrasts that may suffer from poor functional signal to noise ratio.
The results of the conventional second level analyses as well as the inclusion and exclusion analyses were thresholded at an uncorrected p = 0.01 and corrected for multiple testing with a 3D Monte Carlo cluster-threshold estimation as implemented in BVQX using 1000 iterations. For the Monte Carlo simulation, no mask was used to restrict the 3D space to gray matter only. All reported results are significant at a cluster-threshold corrected p-value of 0.05. Clusters that survived the critical cluster size were re-imported into Matlab using BVQX tools. Subsequently, the data were analyzed with tools programmed by one of the authors (Jan Willem Koten). BVQX coordinates were transformed into Talairach space, and the voxel with the peak activation within each significantly activated cluster was extracted.
Finally, the developmental effects on the link between finger representations and numerical processing were studied by analyzing the correlations between age and individual beta weights of the numerical tasks as well as the visually guided finger movement task for all clusters specifically activated only during the visually guided finger movement task (short: finger task) and the numerical tasks (but not the visually guided saccades task). The correlations were Fisher’s-z transformed and averaged over all the voxels of each cluster of interest. Finally, the averaged correlations were retransformed and tested for departure from zero including a Bonferroni correction for the cluster resulting from each inclusion–exclusion analysis.
Results
Behavioral results
Mean accuracy rates were very high for all tasks (0.93−0.96), and reaction times (RT) varied considerably between children. Descriptive statistics for RT and accuracy for the six tasks can be obtained from Table 1.
Table 1.
Descriptive statistics of behavioral results (reaction times in seconds).
| Task | Mean | SD | Range | |
|---|---|---|---|---|
| Visually guided finger movement | Accuracy | 0.96 | 0.03 | 0.88–1.00 |
| RT | 0.71 | 0.18 | 0.40–1.11 | |
| Symbolic comparison | Accuracy | 0.99 | 0.02 | 0.92–1.00 |
| RT | 0.82 | 0.24 | 0.51–1.28 | |
| Non-symbolic comparison | Accuracy | 0.96 | 0.01 | 0.92–0.96 |
| RT | 1.08 | 0.32 | 0.54–1.77 | |
| Symbolic addition | Accuracy | 0.95 | 0.06 | 0.83–1.00 |
| RT | 2.20 | 1.60 | 0.70–5.71 | |
| Non-symbolic addition | Accuracy | 0.93 | 0.06 | 0.75–1.00 |
| RT | 3.84 | 1.60 | 1.24–6.59 | |
| Visual working memory | Accuracy | 0.91 | 0.08 | 0.75–1.00 |
| RT | 2.25 | 0.54 | 1.57–3.80 | |
Significant speed-accuracy trade-offs were not found for any task, although it tended to be significant for the visual working memory task (r = −0.437, p = 0.057). This task was the only one for which accuracy (r = 0.689, p = 0.001), but not RT (r = −0.325, p = 0.162), correlated significantly with age (Bonferroni-corrected α = 0.0024 for all correlations with age or IQ). For all other tasks, age did not correlate with accuracy (all r < −0.31, all p < 0.17) but did correlate with the RT of all tasks (all r ≤ −0.689, all p ≤ 0.001) except for the non-symbolic addition task (r = −0.629, p = 0.003). Estimated IQ did not correlate significantly with the RT (all r ≤ 0.624, all p ≥ 0.004) or accuracy (all r ≥ −0.581, p ≥ 0.009) of any task. Within the accuracy rates (Bonferroni-corrected α = 0.0033), only the accuracy of the finger representation task and the non-symbolic addition task (r = 0.655, p = 0.002) as well as the accuracy of the symbolic and the non-symbolic magnitude comparison tasks were significantly correlated (r = 0.661, p = 0.001; all other r < 0.525, all p > 0.018). Among the RT measures (Bonferroni-corrected α = 0.0033), the RT of the finger representation task was significantly correlated with the RT of both comparison tasks (both r > 0.731, both p < 0.001, all other r ≤ 0.619, all p ≥ 0.004). The RT of the working memory task did not correlate significantly with the RT of any other task (all r ≤ 0.578, all p ≥ 0.008), but the RTs of all four numerical tasks were significantly correlated (all r > 0.723, all p < 0.001).
Partial correlations for all significant correlations controlling for effects of age, estimated IQ, and respective accuracy rates or RT of all other tasks were still significant for accuracy rates of finger representation and non-symbolic addition (r = 0.686, p = 0.010) and the accuracy of symbolic and non-symbolic comparison (r = 0.582, p = 0.046). No other partial correlations remained significant.
In summary, specific behavioral relationships were found between finger representation and non-symbolic addition as well as between symbolic and non-symbolic comparison.
Brain imaging results
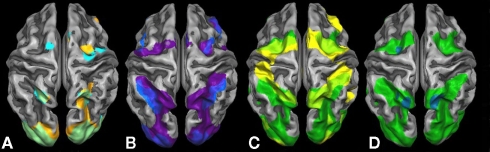
Results of the second level GLM analyses for the six separate task contrasts against rest are presented in Figure 2. The symbolic (light blue) and the non-symbolic (light orange) number comparison task (Figure 2A) showed a highly similar activation pattern located in the dorsal stream of visual processing. In both tasks (overlap shown in light green), lower and higher visual systems were activated bilaterally including the superior posterior aspects of the parietal cortex extending into the medial aspects of the IPS. In the frontal part of the brain, activations for both magnitude comparison tasks were found on the left side corresponding to the FEF (for the symbolic comparison task bilaterally), while overlapping bilateral activations on the medial side of the brain corresponded to the supplementary eye fields (SEF) and SMA activations. In addition, a right insular activation was exclusively found for the non-symbolic number comparison task.
Figure 2.
Brain activation contrasts against rest for all six tasks projected onto a Talairach child template. Brain activations significant at a cluster-threshold corrected p-value of 0.05 are depicted: (A) symbolic (light blue) and non-symbolic (light orange) magnitude comparison; (B) symbolic (dark blue) and non-symbolic (purple) exact addition; (C) visually guided finger movements (yellow) and visually guided saccades (dark green); and (D) visually guided saccades/encoding phase (dark green) and sustained activity phase (turquoise) of the visual working memory task.
Significant brain activations of the symbolic (dark blue) and the non-symbolic (purple) exact addition tasks are shown in Figure 2B. Overlapping brain activations for both addition tasks were found in the lower and higher visual areas including the superior posterior aspects of the parietal cortex extending into the medial and lateral aspects of the IPS. Extended overlap was also found in the bilateral anterior insula, left vPMC, right FEF, and right DLPFC. Finally, bilateral overlap was found on the medial side of the brain including areas that correspond to the SEF and SMA. The symbolic addition task showed more extended activations in the lateral aspects of the IPS and the left DLPFC, whereas the non-symbolic addition task showed higher activations in the left FEF and right vPMC.
Figure 2C shows significant brain activation for the encoding phase of the visual working memory task (visually guided saccades; dark green) and the visually guided finger movement task (yellow). The finger task and the saccades task showed both individualized and overlapping areas of brain activation. Overlapping areas were found in the lower and higher visual areas including the superior posterior aspects of the parietal system extending into the medial aspects of the IPS accumulating in larger rostral IPS activations. Very large parts of the ventral and dorsal PMC, possibly extending into the SEF, were found to be overlapping bilaterally. Additionally, saccade-related activations were found in the ventral visual systems extending into the parieto-occipital sulcus and the lateral aspects of the IPS. (Figure 2D shows the regions active during the sustained activity phase of the visual working memory task, namely the left FEF and bilateral PSPL.) The finger task showed additional activations in finger-related sensory motor systems covering an extended band from the aIPS over the primary somatosensory systems into the primary motor systems on the left side of the brain, while an “interrupted” pattern was found on the right side. Moreover, extended activations were found in the bilateral insular cortex and the right DLPFC for the finger task only. The highly overlapping areas for the visually guided finger task and the visually guided saccade task clearly indicate that purely finger-related aspects of cognition cannot be traced without also employing a visual task. This phenomenon is particularly true for the activation pattern in the IPS that is subdivided into visual and finger-related aspects of cognition.
Further inspection of Figure 2 suggests that the medial aspects of the IPS are activated in all number tasks. This “number area” seems to show overlap with an area that is activated in both the visually guided saccades and the visually guided finger movement task. Moreover, additions seem to activate the lateral aspects of the IPS and show overlap with an area that is activated in the saccade task but not in the finger task. Finally, additions compared to magnitude comparisons seem to activate larger dorsal as well as ventral premotor areas, the FOP, and the DLPFC, which might possibly overlap with motor-related aspects of cognition as activated by the finger task. These impressions were assessed more formally using an inclusion–exclusion analysis approach. The respective results can be found in Figures 3 and 4.
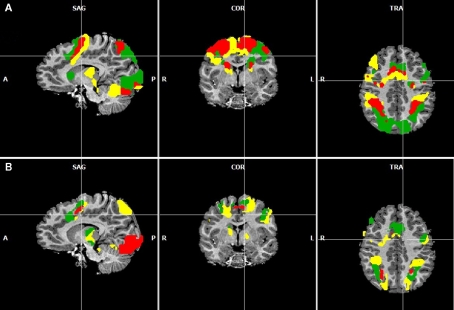
Figure 3.
(A) Overlapping regions for the non-numerical tasks using inclusion and exclusion analyses: regions commonly activated during the visually guided finger movement and saccades task (red), exclusively activated during the saccades task (green), and exclusively activated during the finger task (yellow). (B) Overlapping regions for the numerical tasks using inclusion and exclusion analyses: regions commonly activated during all four numerical tasks (red), regions exclusively activated during symbolic and non-symbolic exact addition (green), and regions exclusively activated during the non-symbolic addition task. All group activations are projected onto a single child brain in Talairach space and are each significant at a cluster-threshold corrected p-value of 0.05.
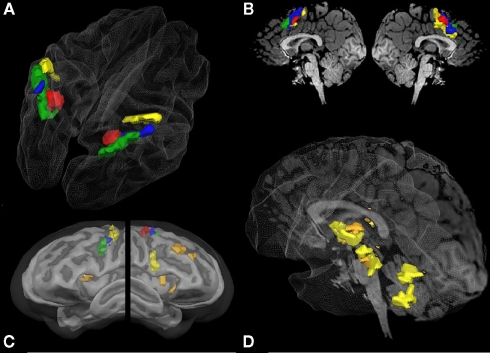
Figure 4.
Overlapping regions between specific numerical and non-numerical tasks using inclusion and exclusion analyses: conjunction of all six tasks (red); areas commonly activated in the visually guided saccades task and the visually guided finger task in conjunction with both addition tasks but not the two magnitude comparison tasks (blue); areas exclusively activated during the saccades task but not the finger task in conjunction with both addition tasks but not the magnitude comparison tasks (green); areas activated exclusively during the finger task in conjunction with both addition tasks (orange); and areas exclusively activated during the finger task and the non-symbolic addition task (yellow). All group activations are projected onto a Talairach child template [(A) parietal activation cluster; (C) lateral frontal activation clusters; (D) subcortical activation clusters] or a single child brain in Talairach space [(B) medial frontal activation clusters; (D) subcortical activation clusters] and are significant at a cluster-threshold corrected p-value of 0.05.
Figure 3A shows areas commonly activated by the visually guided finger movement and the visually guided saccades task (red), exclusively activated by the saccades task (green), and exclusively activated by the finger task (yellow). Figure 3B shows areas commonly activated by all four numerical tasks (red), exclusively activated by both addition tasks (green), and exclusively activated by the non-symbolic addition task (yellow).
It can be observed that areas that showed common activation for both non-numerical tasks and areas showing common activation for all four numerical tasks (depicted in red in both cases) seem to be located in the same IPS region, likely reflecting the polymodal area VIP. Moreover, an area exclusively activated during both the symbolic and the non-symbolic addition tasks (depicted in green in Figure 3B) showed spatial overlap in the LIP with an area that was exclusively activated during the visually guided saccades task (depicted in green in Figure 3A). The area exclusively activated during non-symbolic addition showed spatial overlap with an area that was exclusively activated by the finger task in the very anterior parts of the IPS extending into the wall of the somatotopic cortex (BA2: depicted in yellow in both Figures 3A,B). These specific overlaps are visualized more clearly in Figure 4A for parietal activation clusters (in red, green, and yellow as described above as well as blue for overlapping activation for both non-numerical and both addition tasks but not for the magnitude comparison tasks), in Figure 4B for medial activation clusters, in Figure 4C for frontal activation clusters, and in Figure 4D for subcortical activation clusters. The anatomical labels, cluster volumes, and corresponding Talairach coordinates for peak activations can be found in Tables 2– 6. The estimated cluster thresholds were seven voxels for all clusters.
Table 2.
Anatomical labels and volumes in cubic millimeter of clusters significantly activated in all tasks (depicted in red in Figure 3) with respective Talairach coordinates (xyz) of peak values for all included tasks.
| Anatomical label (volume in mm3) | Visually guided finger movement | Visually guided saccades | Symbolic magnitude comp. | Non-symbolic magnitude comp. | Symbolic exact addition | Non-symbolic exact addition | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bilateral supplementary motor area (1410) | −5 | −3 | 50 | 4 | 3 | 47 | 13 | 3 | 44 | 13 | 3 | 44 | 7 | 12 | 38 | 13 | 6 | 41 |
| Left ventral intraparietal area (889) | −20 | −54 | 44 | −23 | −51 | 38 | −17 | −54 | 38 | −17 | −54 | 41 | −29 | −54 | 41 | −17 | −54 | 38 |
| Right ventral intraparietal area (736) | 28 | −60 | 44 | 28 | −60 | 44 | 28 | −57 | 38 | 31 | −57 | 41 | 31 | −54 | 38 | 31 | −57 | 41 |
| Right frontal eye fields (273) | 31 | −9 | 50 | 31 | −9 | 50 | 31 | −12 | 56 | 31 | −9 | 50 | 34 | −6 | 59 | 34 | −6 | 56 |
Table 6.
Anatomical labels and volumes in cubic millimeter of clusters significantly in the visually guided finger movement and saccades tasks as well as in the symbolic and the non-symbolic exact addition tasks, but not in the symbolic and non-symbolic magnitude comparison tasks (depicted in blue in Figure 3) with respective Talairach coordinates (xyz) of peak values for all included tasks.
| Anatomical label (volume in mm3) | Visually guided finger movement | Visually guided saccades | Symbolic exact addition | Non-symbolic exact addition | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bilateral supplementary motor area (2653) | −8 | −6 | 56 | 1 | 6 | 44 | 7 | 12 | 38 | 16 | 9 | 38 |
| Right intraparietal sulcus (736) | 49 | −39 | 44 | 34 | −51 | 41 | 37 | −48 | 35 | 37 | −48 | 35 |
| Right frontal eye field (438) | 28 | −6 | 44 | 31 | 0 | 53 | 34 | −3 | 56 | 34 | −3 | 53 |
| Left premotor cortex (234) | −44 | −3 | 47 | −47 | 0 | 47 | −44 | 0 | 44 | −38 | −3 | 44 |
| Left intraparietal sulcus (157) | −32 | −54 | 47 | −32 | −54 | 53 | −35 | −54 | 50 | −32 | −51 | 50 |
In addition to activations in the parietal cortex, activation of the frontal and subcortical structures might be of equal importance. Figure 3 visualizes that the brain activity pattern found for the parietal cortex is inversely copied at the medial side of the brain (SMA). In this area, exclusively saccade-related activations are found in the rostral areas, while exclusively finger-related aspects are found in the caudal areas (Figures 3A and 4B). This finding might mirror SEF and SMA-related systems. Activation during addition in this area might also be related to visual and finger representation or to polymodal components in the overlapping parts (Figure 4B). It has indeed been shown that parietal systems project to the medial aspects of the brain (Martin, 1996), making these similarities of activation patterns unsurprising.
Figure 4C shows the results for the inclusion and exclusion analyses for the frontal cortex. Not surprisingly, a cluster activated by all six tasks (red) was found in the FEF, suggesting that organized eye movements are of importance in all tasks. All other reported clusters showed activation during the addition but not the magnitude comparison tasks. In the left hemisphere, three different respective clusters were found originating in the precentral gyrus, extending in a rostral and ventral direction. The most ventral cluster was only active during both addition and the saccades tasks (green), whereas the most dorsal patch in M1 was only active during non-symbolic addition and the finger task (yellow). The intermediate cluster (blue) was activated in both the saccades and finger tasks. Bilateral activation clusters in the insula and in the right DLPF cortex were found for symbolic and non-symbolic addition in conjunction with the finger task but not the saccades task (orange). Furthermore, a cluster in the right vPMC was exclusively activated during the non-symbolic addition and the finger task (yellow).
Furthermore, the addition tasks showed large overlap in subcortical systems, which were exclusively activated by the finger task but not the saccades task (Figure 4D: orange clusters). They included the more ventral basal aspects of the thalamus, the basal ganglia, and substantial parts of the midbrain. For the non-symbolic addition task, the more dorsal aspect of the posterior lobe of the cerebellum was found to be active as well (yellow). Activations in the thalamus and cerebellum may correspond to the respective somatotopic representations of the fingers (Martin, 1996).
Of all the clusters significantly activated only during the finger task and any numerical task (see Tables 3 and 4: depicted in orange and yellow in Figure 4), the overall highest correlation with age was found for the mean activation during the finger task in the smaller right DLPF cortex cluster (r = 0.445, two-sided uncorrected p = 0.0492). No correlation coefficient survived the Bonferroni correction. Therefore, correlations with age were not substantial and never explained more than 20% of the variance of brain activations common to finger representation and number processing.
Table 3.
Anatomical labels and volumes in cubic millimeter of clusters significantly activated only in the visually guided finger movement task as well as in the symbolic and the non-symbolic exact addition tasks, but not during the visually guided saccades task as well as the symbolic and non-symbolic magnitude comparison tasks (depicted in orange in Figure 3) with respective Talairach coordinates (xyz) of peak values for all included tasks.
| Anatomical label (volume in mm3) | Visually guided finger movement | Symbolic exact addition | Non-symbolic exact addition | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Right thalamus (1482) | 10 | −18 | 11 | 19 | −12 | 20 | 13 | −18 | 14 |
| Left frontal operculum (879) | −23 | 15 | 5 | −23 | 15 | 5 | −23 | 15 | 5 |
| Right dorso-lateral prefrontal cortex (778) | 37 | 33 | 32 | 46 | 27 | 32 | 40 | 27 | 35 |
| Left thalamus (746) | −8 | −15 | 8 | −11 | −9 | 17 | −8 | −15 | 8 |
| Right dorso-lateral prefrontal cortex (741) | 28 | 33 | 23 | 37 | 33 | 20 | 28 | 33 | 26 |
| Right frontal operculum/insula (541) | 37 | 15 | 5 | 37 | 12 | 2 | 37 | 15 | 2 |
| Bilateral midbrain (481) | 1 | −24 | −13 | 1 | −24 | −13 | 1 | −21 | −13 |
| Right frontal operculum/insula (329) | 31 | 18 | −1 | 25 | 18 | 2 | 31 | 18 | −1 |
| Left supplementary motor area (197) | −5 | −9 | 56 | −8 | −6 | 59 | 1 | −6 | 56 |
| Bilateral supplementary motor area (172) | 1 | 6 | 41 | 4 | 9 | 41 | 4 | 6 | 41 |
| Right supplementary motor area (171) | 13 | 0 | 50 | 7 | −3 | 53 | 7 | −3 | 53 |
| Right cerebellum (122) | 28 | −60 | −28 | 28 | −66 | −25 | 28 | −60 | −28 |
Table 4.
Anatomical labels and volumes in cubic millimeter of clusters significantly activated only in the visually guided finger movement task and the symbolic exact addition tasks, but in no other task (depicted in yellow in Figure 3) with respective Talairach coordinates (xyz) of peak values for all included tasks.
| Anatomical label (volume in mm3) | Visually guided finger movement | Symbolic exact addition | ||||
|---|---|---|---|---|---|---|
| Right ventral premotor cortex (1327) | 55 | 3 | 26 | 55 | 3 | 17 |
| Bilateral supplementary motor area (1125) | −8 | −12 | 56 | 16 | 6 | 38 |
| Bilateral cerebellum (1099) | 10 | −57 | −13 | 7 | −48 | −13 |
| Right supplementary motor area (1050) | −2 | 0 | 41 | 1 | 0 | 41 |
| Right anterior intraparietal area (920) | 46 | −27 | 53 | 49 | −33 | 50 |
| Bilateral midbrain (796) | 1 | −27 | −13 | 7 | −30 | −10 |
| Left thalamus (792) | −5 | −18 | 8 | −5 | −15 | 8 |
| Left anterior intraparietal area (750) | −44 | −33 | 53 | −44 | −39 | 56 |
| Right cerebellum (733) | 10 | −63 | −19 | 13 | −66 | −19 |
| Right thalamus (650) | 16 | −18 | 8 | 16 | −21 | 8 |
| Left motor area (598) | −38 | −9 | 56 | −41 | −9 | 56 |
Table 5.
Anatomical labels and volumes in cubic millimeter of clusters significantly only in the visually guided saccades task as well as in the symbolic and the non-symbolic exact addition tasks, but not the visually guided finger movement task and the symbolic and non-symbolic magnitude comparison tasks (depicted in green in Figure 3) with respective Talairach coordinates (xyz) of peak values for all included tasks.
| Anatomical label (volume in mm3) | Visually guided saccades | Symbolic exact addition | Non-symbolic exact addition | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Left lateral intraparietal area (3307) | −35 | −48 | 53 | −41 | −51 | 56 | −29 | −54 | 41 |
| Right lateral intraparietal area (1845) | 28 | −69 | 44 | 37 | −51 | 35 | 28 | −72 | 41 |
| Bilateral supplementary motor area (1268) | −5 | 18 | 32 | 10 | 18 | 41 | 1 | 15 | 38 |
| Left ventral premotor cortex (1136) | −44 | 0 | 47 | −47 | 0 | 44 | −47 | 0 | 35 |
| Right frontal eye field (64) | 31 | 3 | 53 | 34 | 0 | 50 | 34 | 0 | 50 |
Finally, we were interested in the non-symbolic and symbolic aspects of number processing and their overlap with saccades- and finger-related brain activation patterns. No cortical area was found to be exclusively active in both symbolic tasks, but not in the non-symbolic numerical tasks. Cortical brain areas exclusively activated during both non-symbolic numerical tasks, but not during the symbolic numerical tasks, showed specific patterns of overlap with the visually guided saccades task (green) and finger movement task (yellow) or with both (red: depicted in Figure 5).
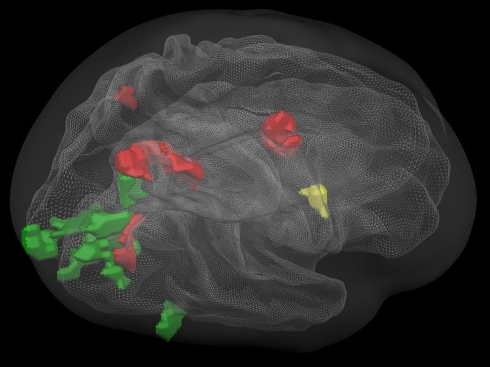
Figure 5.
Overlapping regions between specific non-symbolic numerical (magnitude comparison and exact addition) and non-numerical tasks using inclusion and exclusion analyses: regions commonly activated during all tasks (red); regions commonly activated during the non-symbolic number processing tasks and the finger movement task, but not the saccades task (yellow); regions commonly activated during the non-symbolic number processing tasks and the saccades task, but not the finger movement task (green). All group activations are projected onto a Talairach child template. All clusters are significant at a cluster-threshold corrected p-value of 0.05.
Areas that were exclusively activated during non-symbolic number processing in conjunction with exclusively saccades-related activation (green) were found in bilateral areas of the primary visual cortex and a large cluster in the right hemisphere connecting the lateral occipital complex to the caudal aspects of the IPS via the parieto-occipital sulcus. Overlapping activation with both the visually guided saccades and the finger task (red) included the bilateral posterior eye fields (PEF), the right FEF, and the right parieto-occipital sulcus. Finally, a purely finger-related activation cluster was found in the right ventral precentral sulcus.
Discussion
This study aimed to relate brain activations subserving numerical cognition in children to areas involved in finger representation. Another aim was the identification of areas underlying distinct types of numerical representations by means of inclusion–exclusion analyses using four numerical tasks and two non-numerical localizer tasks.
First, we tried to tease apart modality-specific and polymodal number processing areas in the cortex. The activation patterns we found were highly similar to the findings reported for the monkey as well as for the human brain. The number processing areas related to saccades in the lateral IPS showed high overlap with the monkey LIP area containing number neurons of the accumulating/monotonic magnitude coding type (Roitman et al., 2007), whereas the finger-related number processing areas in the aIPS (extending into the postcentral sulcus) were highly similar to the monkey AIP region (Sawamura et al., 2002) and human homologs (Kaufmann et al., 2008, 2011). The number processing area active during both the finger and the saccades task was found in a similar region to the monkey VIP, possibly related to polymodal number representation (cat brain: Thompson et al., 1970; human brain: Piazza et al., 2007; Dehaene, 2009).
Although these similarities are striking, they may not necessarily be correct. In particular, it has been discussed recently whether the human homolog of the LIP area may be located in the lateral aspects of the IPS (where we found overlapping activation related to saccades and addition; see also Culham and Kanwisher, 2001) or in the superior parietal lobe (where we found overlapping activation for both visually guided saccades and finger movements as well as non-symbolic number processing; see also Grefkes and Fink, 2005). Considering the accumulating characteristics of number neurons in the monkey LIP (Roitman et al., 2007), it may be speculated that these number neurons play a role in the addition processes. Concerning visual processes in the LIP region, one may speculate that the lateral posterior aspects of the IPS are related to the actual encoding of saccades, whereas the PSPL may be related to the maintenance of visual information in the absence of actual vision. An analysis of the visual working memory task during the sustained activity phase indeed showed active areas corresponding to the FEF and the PSPL. However, this discussion has not yet been resolved (Shikata et al., 2008).
The most important result was that the contribution of finger-related systems was stronger for calculation than for magnitude comparison and stronger for non-symbolic exact addition compared to symbolic addition. In our study, activation exclusively related to non-symbolic exact addition (for which counting and ordinal cognitive processes are required) was concordant with exclusively finger-related activation clusters in the bilateral aIPS (extending into the postcentral sulcus), left M1, right ventral precentral sulcus, bilateral SMA, bilateral thalamus, and midbrain as well as the finger-related areas in the cerebellum. (We have no consistent explanation as to why the homolog of the ventral precentral sulcus in the left hemisphere was exclusively activated during the visually guided saccades, but not the visually guided finger movement task). Our results showed that some of the frontal and subcortical regions were also active during symbolic addition, namely the right DLPFC, bilateral insula, aspects of the SMA, as well as the thalamus and midbrain. This putative (visually guided) finger movement network might be an important somatosensory integration system (Piaget, 1952) that is also activated during symbolic additions, which are generally not solved by counting, as the relatively short reaction times show. None of these regions showed decreases (or increases) in activation strength with age, meaning that, contrary to our expectations in our sample (from 6 to 12 years of age), no developmental changes concerning the activation of finger-related brain areas during calculation could be found.
Furthermore, finger-related activation in the ventral precentral sulcus was found to be present during non-symbolic, but not during symbolic, number processing. The very short reaction times for the non-symbolic magnitude comparison task clearly showed that no counting process could be involved in solving this task: 11-year-old children need on average 1.5 s to count five dots and 3 s to count nine dots (Schleifer and Landerl, 2010), whereas it took the slowest child in our sample of 6- to 12-year-old children 1.77 s on average to compare two arrays comprising overall five to nine dots. Therefore, the (right) vPMC may be interpreted as an area responsible for coding canonical hand shapes (and not counting procedures) used for showing numbers up to 10 (in analogy to a so-called “movement vocabulary” coded in the vPMC: Rizzolatti and Lupino, 2001): only the last step of the counting process is a static hand shape or finger posture that represents the exact cardinal aspect of numbers. The specific finger postures may be associated with exact number magnitudes during cognitive development and therefore turn into abstract symbols themselves (Di Luca and Pesenti, 2008). This speculative interpretation has to be taken with caution because we could not directly test this hypothesis with our design. We believe that disentangling the roles of finger counting procedures and canonical hand shapes for (non-symbolic) number processing and calculation will be a worthwhile endeavor for future studies.
In general, accumulating evidence points to the important role of finger representations for the development of exact, non-symbolic addition, possibly mediated by access to exact number magnitude representations for non-symbolic numerosities via the representations of number-related canonical hand shapes (Di Luca and Pesenti, 2008; Kaufmann et al., 2011). In conclusion, finger counting might critically mediate the step from non-symbolic to symbolic and exact number processing and therefore represent an important example of embodied cognition.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
References
- Anderson M. L. (2003). Embodied cognition: a field guide. Artif. Intell. 149, 91–130 10.1016/S0004-3702(03)00056-0 [DOI] [Google Scholar]
- Andres M., Olivier E., Badets A. (2008). Actions, words, and numbers: a motor contribution to semantic processing? Curr. Dir. Psychol. Sci. 17, 313–317 10.1111/j.1467-8721.2008.00597.x [DOI] [Google Scholar]
- Andres M., Seron X., Olivier E. (2007). Contribution of hand motor circuits to counting. J. Cogn. Neurosci. 19, 563–576 10.1162/jocn.2007.19.4.563 [DOI] [PubMed] [Google Scholar]
- Arsalidou M., Taylor M. J. (2011). Is 2 + 2 = 4? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage 54, 2382–2393 10.1016/j.neuroimage.2010.10.009 [DOI] [PubMed] [Google Scholar]
- Binkofski F., Buccino G., Posse S., Seitz R. J., Rizzolatti G., Freund H.-J. (1999). A fronto-parietal circuit for object manipulation in man: evidence from an fMRI-study. Eur. J. Neurosci. 11, 3276–3286 10.1046/j.1460-9568.1999.00753.x [DOI] [PubMed] [Google Scholar]
- Bongard S., Nieder A. (2010). Basic mathematical rules are encoded by primate prefrontal cortex neurons. Proc. Natl. Acad. Sci. U.S.A. 107, 2277–2282 10.1073/pnas.0909180107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brannon E. M., Van de Walle G. A. (2001). The development of ordinal numerical competence in young children. Cogn. Psychol. 43, 53–81 10.1006/cogp.2001.0756 [DOI] [PubMed] [Google Scholar]
- Brass M., Derrfuss J., Forstmann B., von Cramon D. Y. (2005). The role of the inferior frontal junction area in cognitive control. Trends Cogn. Sci. (Regul. Ed.) 9, 314–316 10.1016/j.tics.2005.08.007 [DOI] [PubMed] [Google Scholar]
- Brozzoli C., Ishihara M., Göbel S. M., Salemme R., Rossetti Y., Farnè A. (2008). Touch perception reveals the dominance of spatial over digital representation of numbers. Proc. Natl. Acad. Sci. U.S.A. 105, 5644–5648 10.1073/pnas.0708414105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulheller S., Häcker H. (2002). Coloured Progressive Matrices. Frankfurt: Pearson Assessment [Google Scholar]
- Culham J. C., Kanwisher, Kanwisher N. G. (2001). Neuroimaging of cognitive functions in human parietal cortex. Curr. Opin. Neurobiol. 11, 157–163 10.1016/S0959-4388(00)00191-4 [DOI] [PubMed] [Google Scholar]
- Dehaene S. (2009). Origins of mathematical intuitions. The case of arithmetic. Ann. N. Y. Acad. Sci. 1156, 232–259 10.1111/j.1749-6632.2009.04469.x [DOI] [PubMed] [Google Scholar]
- Di Luca S., Grana A., Semenza C., Seron X., Pesenti M. (2006). Finger-digit compatibility in Arabic numeral processing. Q. J. Exp. Psychol. (Hove) 59, 1648–1663 10.1080/17470210500256839 [DOI] [PubMed] [Google Scholar]
- Di Luca S., Lefèvre N., Pesenti M. (2010). Place and summation coding for canonical and non-canonical finger numeral representations. Cognition 117, 95–100 10.1016/j.cognition.2010.06.008 [DOI] [PubMed] [Google Scholar]
- Di Luca S., Pesenti M. (2008). Masked priming effect with canonical finger numeral configurations. Exp. Brain Res. 185, 27–39 10.1007/s00221-007-1132-8 [DOI] [PubMed] [Google Scholar]
- Domahs F., Krinzinger H., Willmes K. (2008). Mind the gap between both hands: evidence for internal finger-based number representations in children’s mental calculation. Cortex 44, 359–367 10.1016/j.cortex.2007.08.001 [DOI] [PubMed] [Google Scholar]
- Domahs F., Moeller K., Huber S., Willmes K., Nuerk H.-C. (2010). Embodied numerosity: implicit hand-based representations influence symbolic number processing across cultures. Cognition 116, 251–266 10.1016/j.cognition.2010.05.007 [DOI] [PubMed] [Google Scholar]
- Dormal V., Andres M., Dormal G., Pesenti M. (2010). Mode-dependent and mode-independent representations of numerosity in the right intraparietal sulcus. Neuroimage 52, 1677–1686 10.1016/j.neuroimage.2010.04.254 [DOI] [PubMed] [Google Scholar]
- Fayol M., Seron X. (2005). “About numerical representations: insights from neuropsychological, experimental and developmental studies,” in Handbook of Mathematical Cognition, ed. Campbell J. I. D. (New York: Psychology Press; ), 3–22 [Google Scholar]
- Fischer M. H. (2008). Finger counting habits modulate spatial-numerical associations. Cortex 44, 386–392 10.1016/j.cortex.2007.08.004 [DOI] [PubMed] [Google Scholar]
- Fischer M. H., Brugger P. (2011). When digits help digits: spatial-numerical associations point to finger counting as prime example of embodied cognition. Front. Psychol. 2:260. 10.3389/fpsyg.2011.00260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- FitzGerald M. J. T. (1985). Neuroanatomy: Basic and Applied. London: Baillière Tindall [Google Scholar]
- Friston K. J., Penny W. D., Glaser D. E. (2005). Conjunction revisited. Neuroimage 25, 661–667 10.1016/j.neuroimage.2005.01.013 [DOI] [PubMed] [Google Scholar]
- Ghosh S. S., Kakunoori S., Augustinack J., Nieto-Castanon A., Kovelman I., Gaab N., Christodoulou J. A., Triantafyllou C., Gabrieli J. D., Fischl B. (2010). Evaluating the validity of volume-based and surface-based brain image registration for developmental cognitive neuroscience studies in children 4 to 11 years of age. Neuroimage 53, 85–93 10.1016/j.neuroimage.2010.05.075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giedd J. N., Blumenthal J., Jeffries N. O., Castellanos F. X., Liu H., Zijdenbos A., Paus T., Evans A. C., Rapoport J. L. (1999). Brain development during childhood and adolescence: a longitudinal MRI study. Nat. Neurosci. 2, 861–863 10.1038/13158 [DOI] [PubMed] [Google Scholar]
- Gracia-Bafalluy M., Noël M. P. (2008). Does finger training increase young children’s numerical performance? Cortex 44, 368–375 10.1016/j.cortex.2007.08.020 [DOI] [PubMed] [Google Scholar]
- Grefkes C., Fink G. R. (2005). The functional organization of the intraparietal sulcus in humans and monkeys. J. Anat. 207, 3–17 10.1111/j.1469-7580.2005.00426.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrington D. L., Rao S. M., Haaland K. Y., Bobholz J. A., Mayer A. R., Binder J. R., Cox R. W. (2000). Specialized neural systems underlying representations of sequential movements. J. Cogn. Neurosci. 12, 56–77 10.1162/08989290051137602 [DOI] [PubMed] [Google Scholar]
- Haslinger B., Erhard P., Weilke F., Ceballos-Baumann A. O., Bartenstein P., von Einsiedel H., Schwaiger M., Conrad B., Boecker H. (2002). The role of lateral premotor–cerebellar–parietal circuits in motor sequence control: a parametric fMRI study. Brain Res. Cogn. Brain Res. 13, 159–168 10.1016/S0926-6410(01)00104-5 [DOI] [PubMed] [Google Scholar]
- Kansaku K., Carver B., Johnson A., Matsuda K., Sadato N., Hallett M. (2007). The role of the human premotor cortex in counting successive stimuli. Exp. Brain Res. 178, 339–350 10.1007/s00221-006-0736-8 [DOI] [PubMed] [Google Scholar]
- Kaufmann L., Vogel S. E., Wood G., Kremser C., Schocke M., Zimmerhackl L. B., Koten J. W. (2008). A developmental fMRI study of nonsymbolic numerical and spatial processing. Cortex 44, 376–385 10.1016/j.cortex.2007.11.009 [DOI] [PubMed] [Google Scholar]
- Kaufmann L., Wood G., Rubinsten O., Henik A. (2011). Meta-analyses of developmental fMRI studies investigating typical and atypical trajectories of number processing and calculation. Dev. Neuropsychol. 36, 763–787 10.1080/87565641.2010.549884 [DOI] [PubMed] [Google Scholar]
- Knops A., Thirion B., Hubbard E., Michel V., Dehaene S. (2009). Recruitment of an area involved in eye movements during mental arithmetic. Science 324, 1583–1585 10.1126/science.1171599 [DOI] [PubMed] [Google Scholar]
- Koten J. W., Wood G., Hagoort P., Goebel R., Propping P., Willmes K., Boomsma D. I. (2009). Genetic contribution to variation in cognitive function: an fMRI study in twins. Science 27, 1737–1740 10.1126/science.1167371 [DOI] [PubMed] [Google Scholar]
- Krinzinger H., Koten J. W., Hennemann J., Schueppen A., Sahr K., Arndt D., Konrad K., Willmes K. (2011). Sensitivity, reproducibility, and reliability of self-paced versus fixed stimulus presentation in an fMRI study on exact, non-symbolic arithmetic in typically developing children aged between 6 and 12 years. Dev. Neuropsychol. 36, 721–740 10.1080/87565641.2010.549882 [DOI] [PubMed] [Google Scholar]
- Manthey S., Schubotz R. I., von Cramon D. Y. (2003). Premotor cortex in observing erroneous action: an fMRI study. Brain Res. Cogn. Brain Res. 15, 296–307 10.1016/S0926-6410(02)00201-X [DOI] [PubMed] [Google Scholar]
- Martin J. H. (1996). Neuroanatomy: Text and Atlas, 2nd Edn Stanford: Appleton and Lange [Google Scholar]
- Nichols T., Brett M., Andersson J., Wager T., Poline J.-B. (2005). Valid conjunction with the minimum statistic. Neuroimage 25, 653–660 10.1016/j.neuroimage.2004.12.005 [DOI] [PubMed] [Google Scholar]
- Niedenthal P. M., Barsalou L. W., Winkielman P., Krauth-Gruber S., Ric F. (2005). Embodiment in attitudes, social perception, and emotion. Pers. Soc. Psychol. Rev. 9, 184–211 10.1207/s15327957pspr0903_1 [DOI] [PubMed] [Google Scholar]
- Noël M. P. (2005). Finger agnosia: a predictor of numerical abilities in children? Child Neuropsychol. 11, 413–430 10.1080/09297040590951550 [DOI] [PubMed] [Google Scholar]
- Pesenti M., Thioux M., Seron X., DeVolder A. (2000). Neuroanatomical substrates of Arabic number processing, numerical comparison, and simple addition: a PET study. J. Cogn. Neurosci. 12, 461–479 10.1162/089892900562273 [DOI] [PubMed] [Google Scholar]
- Piaget J. (1952). The Child’s Conception of Number. London: Routledge and Kegan Paul [Google Scholar]
- Piazza M., Pinel P., Dehaene S. (2007). A magnitude code common to numerosities and number symbols in human parietal cortex. Neuron 53, 293–305 10.1016/j.neuron.2006.11.022 [DOI] [PubMed] [Google Scholar]
- Price C. J., Moore C. J., Friston K. J. (1997). Subtractions, conjunctions, and interactions in experimental design of activation studies. Hum. Brain Mapp. 5, 264–272 [DOI] [PubMed] [Google Scholar]
- Price G. R., Ansari D. (2011). Symbol processing in the left angular gyrus: evidence from passive perception of digits. Neuroimage 57, 1205–1211 10.1016/j.neuroimage.2011.05.035 [DOI] [PubMed] [Google Scholar]
- Rizzolatti L., Lupino G. (2001). The cortical motor system. Neuron 31, 889–901 10.1016/S0896-6273(01)00423-8 [DOI] [PubMed] [Google Scholar]
- Roitman J. D., Brannon E. M., Platt M. J. (2007). Monotonic coding of numerosity in Macaque lateral intraparietal area. PLoS Biol. 5, e208. 10.1371/journal.pbio.0050208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santens S., Roggeman C., Fias W., Verguts T. (2010). Number processing pathways in human parietal cortex. Cereb. Cortex 20, 77–88 10.1093/cercor/bhp080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M., Cattaneo L., Rizzolatti G., Gallese V. (2007). Numbers within our hands: modulation of corticospinal excitability of hand muscles during numerical judgment. J. Cogn. Neurosci. 19, 684–693 10.1162/jocn.2007.19.4.684 [DOI] [PubMed] [Google Scholar]
- Sato M., Lalain M. (2008). On the relationship between handedness and hand-digit mapping in finger counting. Cortex 44, 393–399 10.1016/j.cortex.2007.08.005 [DOI] [PubMed] [Google Scholar]
- Sawamura H., Shima K., Tanji J. (2002). Numerical representation for action in the parietal cortex of the monkey. Nature 451, 918–922 10.1038/415918a [DOI] [PubMed] [Google Scholar]
- Schleifer P., Landerl K. (2010). Subitizing and counting in typical and atypical development. Dev. Sci. 14, 280–291 [DOI] [PubMed] [Google Scholar]
- Schubotz R. I., von Cramon D. Y. (2001). Interval and ordinal properties of sequences are associated with distinct premotor areas. Cereb. Cortex 11, 210–222 10.1093/cercor/11.3.210 [DOI] [PubMed] [Google Scholar]
- Shikata E., McNamara A., Sprenger A., Hamzei F., Glauche V., Büchel C., Binkofski F. (2008). Localization of human intraparietal areas AIP, CIP, and LIP using surface orientation and saccadic eye movement tasks. Hum. Brain Mapp. 29, 411–421 10.1002/hbm.20396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talairach J., Tournoux P. (1988). Co-Planar Stereotactic Atlas of the Human Brain. Stuttgart: Thieme Medical Publishers [Google Scholar]
- Thompson R. F., Mayers K. S., Robertson R. T., Pattersion C. (1970). Number coding in association cortex of the cat. Science 168, 271–273 10.1126/science.168.3928.271 [DOI] [PubMed] [Google Scholar]
- Venkatraman V., Ansari D., Chee M. W. L. (2005). Neural correlates of symbolic and non-symbolic arithmetic. Neuropsychologia 43, 744–753 10.1016/j.neuropsychologia.2004.08.005 [DOI] [PubMed] [Google Scholar]
- Wilson M. (2002). Six views of embodied cognition. Psychon. Bull. Rev. 9, 625–636 10.3758/BF03196314 [DOI] [PubMed] [Google Scholar]
- Xu B., Grafman J., Gaillard W. D., Ishii K., Vega-Bermudez F., Pietrini P., Reeves-Tyer P., DiCamillo P. T. (2001). Conjoint and extended neural networks for the computation of speech codes: the neural basis of selective impairment in reading words and pseudowords. Cereb. Cortex 11, 267–277 10.1093/cercor/11.3.267 [DOI] [PubMed] [Google Scholar]