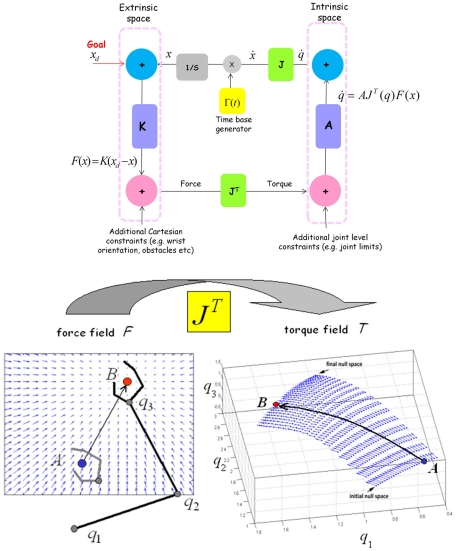
Figure 1.

Top panel. Basic kinematic network that implements the passive motion paradigm for a simple kinematic chain (as the arm). In this simple case, the network is grouped into two motor spaces (extrinsic or end effector space and intrinsic or arm joint space). Each motor space consists of a generalized displacement node (blue) and a generalized force node (pink). Vertical connections (purple) denote impedances (K: Stiffness, A: Admittance) in the respective motor spaces and horizontal connections denote the geometric relation between the two motor spaces represented by the Jacobian (Green). The goal induces a force field that causes incremental elastic configurations in the network analogous to the coordination of a marionette with attached strings. The network also includes a time base generator which endows the system with terminal attractor dynamics: this means that equilibrium is not achieved asymptotically but in finite time. External and internal constraints (represented as other task-dependent force/torque fields) bias the path to equilibrium in order to take into account suitable “penalty functions.” This is a multi-referential system of action representation and synergy formation, which integrates a Forward and an Inverse Internal Model. Bottom panel. The figure illustrates the key element of the architecture of Figure 1 for solving the degrees of freedom problem, namely the mapping of the “force field,” defined in the extrinsic space and applied to the end-effector, into the corresponding “torque field,” defined in the intrinsic space and applied to the joints. The mapping is implemented by means of the transpose Jacobian matrix of the kinematic transformation. Dimensionality reduction is obtained implicitly by letting the internal model “slide” in the torque field. Each point of the trajectory in the extrinsic space corresponds to a whole manifold in the intrinsic space (the “null space” of the kinematic transformation). The equilibrium point in the force field corresponds to an equilibrium manifold in the torque field. The selection among the infinite number of possible targets is carried out implicitly by the combination of different force/torque fields.