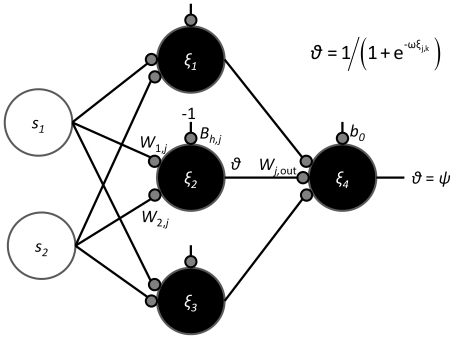
Figure 2. The architecture of the ANNs used in the simulations.

Sensory nodes (open) simply propagate the signals elicited by the resource. Each hidden node j, j = 1,2,3 in the second layer has three ‘synaptic’ weights associated with it: w _1j and w _2j weight the inputs from sensory nodes 1 and 2 respectively and w_{j out} weights the value of the output entering the third layer output node (shown for the middle node only). Further, the hidden nodes have bias weights b_hj, and the output node the bias weight b_o connecting an input of −1. Thus, each perceptron has a representation [w ₁, w ₂, w ₃, w _o],where w _j = (w _1j, w _2j, b_{h j}, w_{j out}) for j = 1,2,3, are the hidden node values and w _o = b _o is the output node value (seen as colors in Fig. 3). The output θ that determines the response of each node is given by the sigmoidal threshold function (upper right corner) where, for sufficiently large ω (here = 4), an internal activity ξ_jk<0 produces output close to 0, otherwise a value close to 1. For a hidden node j = 1,2,3 with niche (host) k's signal applied, the activity values are determined by ξ_jk = (s_{k 1} w _1,j+s_{k 2} w _2,j−b_hj) and for the output neuron by ξ _4k = (θ _1k w _1,out+θ _2k w _2,out+θ _3k w _3,out−b ₀). The output of the perceptron (ψ) is hence between 0 and 1 and interpreted as ‘approximately 0⇒avoid niche’ and ‘approximately 1⇒exploit niche’.