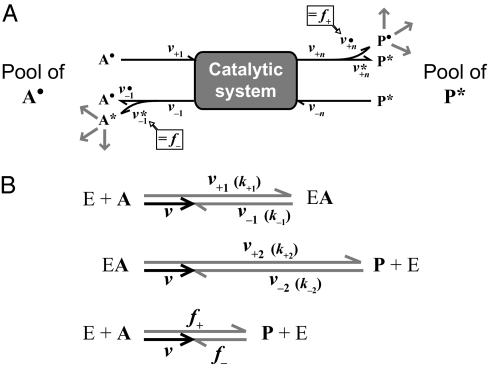
Fig. 3.
Depiction of forward and back flux during the net reaction A → P in a steady state catalytic system with reversible but otherwise unknown internal reactions. Such a system can consist of an entire pathway (A) or a single enzymatic reaction (B; E + A → EA → P + E) (Figs. S4 and S5). All reactions, including uptake or binding and release, are reversible. Arrows indicate rates (velocities). The forward (v+) and back (v−) rates correspond to individual steps in a catalytic system. The index n refers to the number of forward and backward fluxes (B; n = 2 for a single enzymatic reaction) (Fig. S5). A description of abbreviations is given in Table S3. (A) Catalytic system: the fate of substrate and product is followed by the different labels (A•, P*) of the initial pools. Release of A and P includes both the returned fraction that never reached the other side (v•–1, v*+n), and the fraction directly derived from the other side (v•+n, v*–1). Forward (f+) and back (f−) flux are the concentrations (amounts per investigated volume) of P• and A* most recently derived per time from A• and P*, respectively. Hence, return to the side of their origin with progressing reaction is neglected by examining a short time interval (A* in A• and P• in P* remaining very dilute). (B) Vector model for rates in a single enzymatic reaction (E + A → EA → P + E) (Fig. S5). The sizes of rates are indicated by lengths of arrows. The same net rate (v) is the difference of uptake (binding) and release of substrate (v+1, v−1) and product (v+2, v−2) as well as the difference between forward and back flux (f+, f−). The rate constants for a single enzymatic reaction, k+1, k−1, k+2, k−2, and the actual concentrations determine v+1, v−1, v+2, v−2, respectively. The vector model was calculated for the enzymatic reaction using (in rate units): v+1 = 6, v−1 = 4, v+2 = 9, v−2 = 7; result: v = 2, f+ = 4.15, f− = 2.15 (Eqs. S35 and S36).