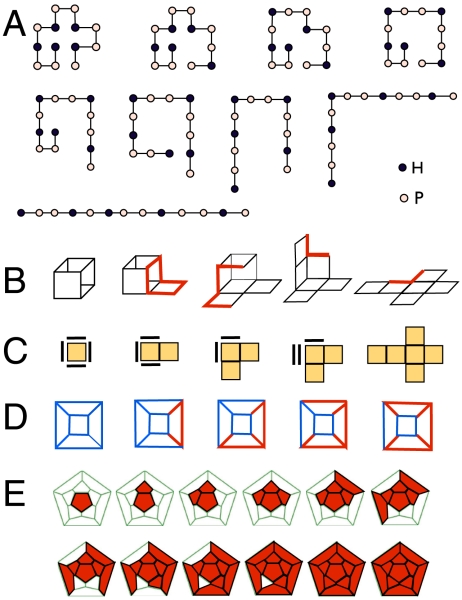
Fig. 6.

Comparison of the discrete geometry of three self-assembly models. (A) Unfolding an HP chain. A compact HP chain on a 2D lattice is unfolded by breaking secondary HH bonds between topological neighbors. At each step, secondary bonds break and/or the chain reduces its discrete curvature. The compact configuration is chosen from ref. 31. The motion of the chain through kink jumps and rigid rotations is adapted from ref. 32. (B–D) Several representations of unfolding a cube. At each step, all edges linked at a vertex connection are cut so that a face is free to rotate rigidly through the dihedral angle, which gives faces linked through vertices but not edges (topological neighbors). (B) A perspective view. (C) A convenient schematic for the plan view that is used in Fig. 7. (D) Unfolding as two-color evolution on the graph of the cube: Cut edges are red and constitute a tree that grows at each step. Unfolding is complete when the tree is spanning. (E) Viral capsid assembly. Intermediate stages in the formation of a dodecahedral viral capsid following refs. 30 and 33. At each stage, a new face is added and congruent arrangements correspond to the same intermediate.