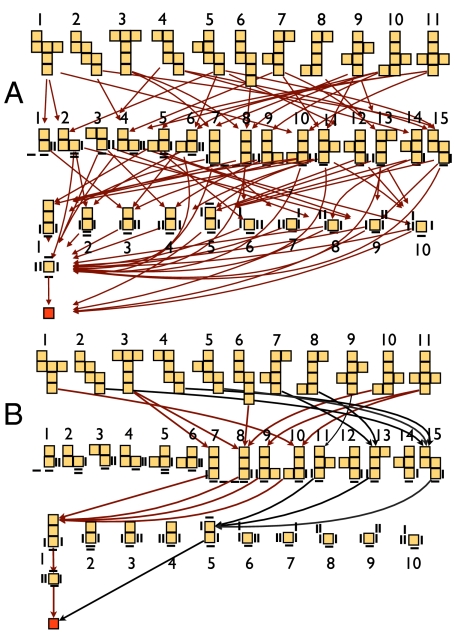
Fig. 7.

(A) Computed configuration space and folding pathways for the cube. Partially folded intermediates and all folding pathways for the cube computed by the gluing at vertex connections algorithm. Multiplicity of edges connecting intermediates is not shown. Double bars denote vertically stacked faces. (B) Geodesics and dominant intermediates. Geodesic pathways between each net and the cube computed using Eq. 1. The dominant intermediates are 1 and 5 in the third row. In this discrete model, nets 1, 3, 6, 10, and 11 fold through intermediate 1, and nets 2, 4, 5, 7, 8, and 9 fold through intermediate 5.