Figure 1. An example of how to tune the link weights to change the node centrality scores.

The graph G with N = 4 nodes and K = 5 links shown in panel (a) is strongly-connected and has an eigenvector centrality c₀ = {0.18, 0.33, 0.27, 0.22}. By ranking the nodes according to the components of c₀, we obtain that node 2 is the most central one, followed in order by node 3, node 4, and node 1. We can now set the weights of the five links ω = {ω₁, ω₂, ω₃, ω₄, ω₅} in such a way that equation (1) is satisfied for any given centrality vector c ≠ c₀. For instance, we can get a weighted network G_ω in which all nodes have the same centrality, by solving equation (1) with a centrality vector c = {1/4, 1/4, 1/4, 1/4} and ρ = 3.0. We obtain a vector of weights: ω = {α, 3, 3, 3, 3 − α} which, for 0 < α < 3, guarantees that all the link weights of the graph are positive. The resulting network G_ω is shown in panel (b). As expected, we have K − N = 1 free parameter (namely α) since the graph has N = 4 nodes and K = 5 links. Instead, if we want to reverse the original node ranking we can solve the system 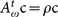with a centrality vector c = {0.5, 0.05, 0.2, 0.25}. Notice that, in this case, the ranking induced by c is exactly the opposite of the one induced by c₀: now node 1 is the most central one, followed in order by node 4, node 3, and node 2. The solution of equation (2) gives ω = {α, 12, 15/4, 6, (3 – 10α)/5}, corresponding to a weighted network G_ω with all positive weights whenever 0 < α < 3/10. The resulting network is shown in panel (c).