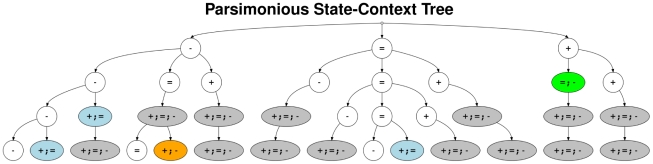
Figure 5. State-context tree of a parsimonious fourth-order HMM.
Parsimonious state-context tree selected among the best parsimonious HMMs of order four at a fixed FPR of 2.5% in Figure 4b. Each path from the root node at the top of the tree to a leaf node at the bottom of the tree represents a set of state-contexts defined to share common transition parameters in the transition matrix 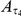 of the selected model. The three nodes directly under the root node represent the possible current states of the selected parsimonious fourth-order HMM, and the subtrees under these three nodes represent the influence of predecessor states on a state-transition from one of these current states to a next state. Fusions of nodes are highlighted in different colors. White nodes represent unfused nodes characterizing important states for a state-transition. Blue, orange, and green nodes represent partially fused states of equal importance for a state-transition. Grey nodes represent completely fused nodes defining that the corresponding position in a state-context has no influence on a state-transition. The states ‘
of the selected model. The three nodes directly under the root node represent the possible current states of the selected parsimonious fourth-order HMM, and the subtrees under these three nodes represent the influence of predecessor states on a state-transition from one of these current states to a next state. Fusions of nodes are highlighted in different colors. White nodes represent unfused nodes characterizing important states for a state-transition. Blue, orange, and green nodes represent partially fused states of equal importance for a state-transition. Grey nodes represent completely fused nodes defining that the corresponding position in a state-context has no influence on a state-transition. The states ‘ ’ and ‘
’ and ‘ ’ of the selected model are still representing some fourth-order transition probabilities, whereas only second-order transition probabilities remain for state ‘
’ of the selected model are still representing some fourth-order transition probabilities, whereas only second-order transition probabilities remain for state ‘ ’. The selected parsimonious fourth-order HMM has a model complexity of 14 leaf nodes leading to 42 different transition parameters in
’. The selected parsimonious fourth-order HMM has a model complexity of 14 leaf nodes leading to 42 different transition parameters in 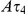 . This is much less than for a corresponding fourth-order HMM with 81 leaf nodes in a complete state-context tree representing 243 transition parameters.
. This is much less than for a corresponding fourth-order HMM with 81 leaf nodes in a complete state-context tree representing 243 transition parameters.