Computer-aided detection of clustered microcalcifications in digital breast tomosynthesis: A 3D approach

Abstract

Purpose: To design a computer-aided detection (CADe) system for clustered microcalcifications in reconstructed digital breast tomosynthesis (DBT) volumes and to perform a preliminary evaluation of the CADe system.

Methods: IRB approval and informed consent were obtained in this study. A data set of two-view DBT of 72 breasts containing microcalcification clusters was collected from 72 subjects who were scheduled to undergo breast biopsy. Based on tissue sampling results, 17 cases had breast cancer and 55 were benign. A separate data set of two-view DBT of 38 breasts free of clustered microcalcifications from 38 subjects was collected to independently estimate the number of false-positives (FPs) generated by the CADe system. A radiologist experienced in breast imaging marked the biopsied cluster of microcalcifications with a 3D bounding box using all available clinical and imaging information. A CADe system was designed to detect microcalcification clusters in the reconstructed volume. The system consisted of prescreening, clustering, and false-positive reduction stages. In the prescreening stage, the conspicuity of microcalcification-like objects was increased by an enhancement-modulated 3D calcification response function. An iterative thresholding and 3D object growing method was used to detect cluster seed objects, which were used as potential centers of microcalcification clusters. In the cluster detection stage, microcalcification candidates were identified using a second iterative thresholding procedure, which was applied to the signal-to-noise ratio (SNR) enhanced image voxels with a positive calcification response. Starting with each cluster seed object as the initial cluster center, a dynamic clustering algorithm formed a cluster candidate by including microcalcification candidates within a 3D neighborhood of the cluster seed object that satisfied the clustering criteria. The number, size, and SNR of the microcalcifications in a cluster candidate and the cluster shape were used to reduce the number of FPs.

Results: The prescreening stage detected a cluster seed object in 94% of the biopsied microcalcification clusters at a threshold of 100 cluster seed objects per DBT volume. After clustering, the detection sensitivity was 90% at 15 marks per DBT volume. After FP reduction, at 85% sensitivity, the average number of FPs estimated using the data set containing microcalcification clusters was 3.8 per DBT volume, and that estimated using the data set free of microcalcification clusters was 3.4. The detection performance for malignant microcalcification clusters was superior to that for benign clusters.

Conclusions: Our study indicates the feasibility of the 3D approach to the detection of clustered microcalcifications in DBT and that the newly designed enhancement-modulated 3D calcification response function is promising for prescreening. Further work is needed to assess the generalizability of our approach and to improve its performance.

INTRODUCTION

Digital breast tomosynthesis (DBT) is a promising new modality for detection and diagnosis of breast cancer. DBT imaging involves acquiring projection views (PVs) of the compressed breast over a range of projection angles using a full-field digital mammography (FFDM) detector. Each PV can be obtained using a fraction of the x-ray exposure used in conventional mammography so that the total DBT dose can be comparable with or slightly higher than that of mammography. A variety of techniques have been used to reconstruct the DBT volume from the acquired PVs.^{1, 2, 3, 4, 5, 6, 7} Since the PVs in a DBT scan are acquired only within a limited range of acquisition angles of the compressed breast, the reconstructed 3D DBT volume contains artifacts due to missing information, regardless of the reconstruction technique applied. Despite reconstruction artifacts, DBT is considered to have a strong potential to improve breast imaging, by reducing the camouflaging effect of the overlapping fibroglandular breast tissue that is usually a limiting factor for lesion detection and characterization in mammography. The potential of DBT in comparison to or as an adjunct to mammography has been demonstrated by several observer studies.^{8, 9, 10, 11, 12}

Computer-aided detection (CADe) systems for cancer detection in mammography have been under development for over two decades and have been commercially available for over a decade. Based on Medicare data, CAD was used in 74% of screening mammographic studies that were performed in 2008.¹³ The effect of CADe on radiologists’ cancer detection performance has been investigated in a number of prospective clinical trials.^{14, 15, 16, 17, 18, 19, 20, 21, 22, 23} Two of the studies with historical controls^{16, 21} did not find a major effect or found a large increase in the call-back rate with CADe; however, other studies^{14, 15, 17, 18, 19, 20, 22, 23} found an increase in sensitivity accompanied by a moderate increase in the call-back rate.

As a new modality, a number of important issues concerning DBT are still under investigation including how DBT can be optimized for breast cancer detection and diagnosis, and how it will fit into the current breast imaging practice. Some of these issues are related to the development and use of CADe. Similar to mammography, there may be lesions missed by radiologists in DBT due to a number of factors, and a consistent second reader may be helpful. Because of the large volume of image data needed to be interpreted in DBT, the chance of missing cancers may not be negligible. CADe may be of particular interest in DBT for microcalcification detection. The detection of microcalcification clusters by radiologists in DBT volumes may be more difficult compared with mammography for two reasons: First, the cluster of microcalcifications may be separated into several reconstructed slices, the number of microcalcifications on each slice will be fewer, making it less conspicuous. Although visualization techniques such as maximum intensity projection (MIP) or slab view may alleviate this problem, these techniques may also cause image blur, and their optimal parameter settings are currently unknown. Second, the microcalcifications may appear blurred due to many factors that can cause blurring in DBT reconstruction, including inaccuracy in the system geometry and the projection model, a range of oblique incidence angles to the detector, focal spot motion and patient motion. A recent study by Spangler et al.²⁴ found that the detection performance of radiologists for microcalcification clusters was higher in FFDM compared with DBT, although the difference did not reach statistical significance for the data set used in that study. In addition to the radiologists’ detection performance, searching for microcalcification clusters in a 3D DBT volume may be more demanding than on mammograms and false negatives may not be negligible. For these reasons, it is expected that CADe may play an even more important role in microcalcification detection in DBT than in mammography.

A number of studies investigated the development of CADe techniques for the detection of masses in DBT.^{25, 26, 27, 28, 29} Compared with the detection of masses, studies investigating the detection of microcalcification clusters on DBT are more preliminary.^{30, 31, 32, 33} Reiser et al.³⁰ investigated the detection of microcalcifications on individual PVs. The detected microcalcifications were then backprojected into the 3D volume. A second-stage detection was performed after this 3D volume was transformed using MIP. False-positive reduction was performed with features extracted from the PVs, followed by 3D clustering. On a data set of 30 image sets with microcalcification clusters and 30 image sets without visible findings, their detection method achieved a sensitivity of 86% with 1.3 false-positive (FP) clusters per DBT volume. Bernard et al.³¹ developed an algorithm for the detection of microcalcification clusters on filtered back-projection reconstructed slices. The voxel contrast was enhanced by convolving the image volume with a Mexican hat wavelet at a specific scale. A voxel was selected as a candidate based on its contrast and the local noise level. A set of scales covering the microcalcification size range was used for the Mexican hat. On a data set of 13 DBT volumes containing microcalcification clusters and 37 normal DBT volumes, their method had a sensitivity of 85% at an average of 1.4 FP marks per breast volume. Park et al.³² compared two preliminary detection methods. The first method detected microcalcification clusters on the individual PVs, and the second method detected clusters on the individual reconstructed slices. Both methods then grouped the detected clusters using location information. The first method detected 14 of 20 (70%) clusters seen on the PV images with an average of 3.99 FPs per DBT volume. The second method detected 35 of 40 (86%) of clusters seen on the reconstructed slices with an average of 15.9 FPs per DBT volume. In our pilot study, we investigated the detection of microcalcification clusters in the reconstructed DBT volume using 3D multiscale filtering and SNR enhancement.³³ On a data set of two-view DBTs of 39 breasts containing microcalcification clusters, a view-based sensitivity of 80% (59/74) was achieved at 2.0 FPs per DBT volume. In this paper, we expanded this preliminary study by almost doubling the data set size for DBT with clustered microcalcifications. We also investigated the effects of filter parameters for both multiscale Hessian enhancement and SNR enhancement and the effect of clustering, and compared the detection performance of the enhancement-modulated 3D calcification response function with that of using SNR enhancement alone. An independent data set of DBTs was also collected to evaluate the FP rate on images free of clustered microcalcifications.

METHODS AND MATERIALS

The DBT scans were acquired with a GE GEN2 prototype system in the breast imaging research laboratory at the University of Michigan. The DBT system acquires 21 PV images over a ±30 angular range in 3 increments in a step-and-shoot operation. Rh target and Rh filter are used for breasts of all thicknesses. The DBT system has a CsI/aSi active matrix flat panel digital detector with dimensions of 19.20 cm × 23.04 cm and a pixel pitch of 0.1 mm × 0.1 mm. The digital detector is stationary during image acquisition. The dose per DBT view was set to be about 1.5 times that of a single-view conventional mammogram in this prototype DBT system. The DBT volumes were reconstructed at 1 mm slice interval using the simultaneous algebraic reconstruction technique (SART), with a relaxation parameter λ of 0.5 and a single iteration.⁴

Data Set

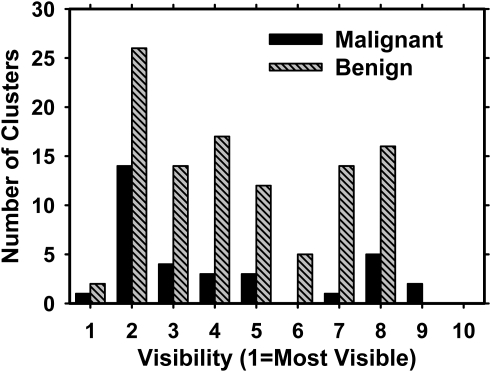
The subject recruitment protocol was IRB approved. Breast imaging patients in our health system who were recommended for breast biopsy based on suspicious mammographic microcalcifications were eligible. Written informed consent was obtained from each subject. DBT scans of the breast were acquired in both craniocaudal (CC) and mediolateral oblique (MLO) views before biopsy was performed. For this study, we collected two-view DBT scans of 72 breasts containing microcalcifications. The location of the biopsy-proven microcalcification cluster was marked by a 3D box in each DBT volume by an experienced Mammography Quality Standards Act (MQSA) radiologist using the clinical mammograms and the biopsy report as references. A total of 139 microcalcification clusters were identified on the 144 DBT scans. In five breasts, the microcalcification cluster was visible only in one of the DBT views. The radiologist also subjectively rated the visibility of the microcalcification clusters on a scale of 1 to 10, where 1 corresponded to the most visible cluster. Figure 1 shows the histogram of visibility ratings for the 139 visible clusters. Of the 72 breast biopsies, 17 of the clusters were found to be malignant and 55 benign. This data set is referred to as the abnormal data set.

Figure 1.

Visibility of the malignant and benign microcalcification clusters on the DBT volume, as rated by a breast radiologist experienced in the interpretation of mammograms and DBT. A rating of 1 corresponded to the most visible clusters. The malignant and benign clusters had average visibilities of 4.0 and 4.5, respectively.

To investigate the number of FPs generated by our CAD system on cases that were free of microcalcification clusters, we used a data set of two-view DBT scans from 38 breasts (76 DBT volumes). These DBTs were acquired from subjects who were scheduled for biopsy due to a suspicious mass. The cases were verified to be free of microcalcification clusters by the same experienced radiologist. For the purposes of this study, these cases are referred to as the “normal data set” since they did not contain any microcalcification clusters,

Detection algorithm

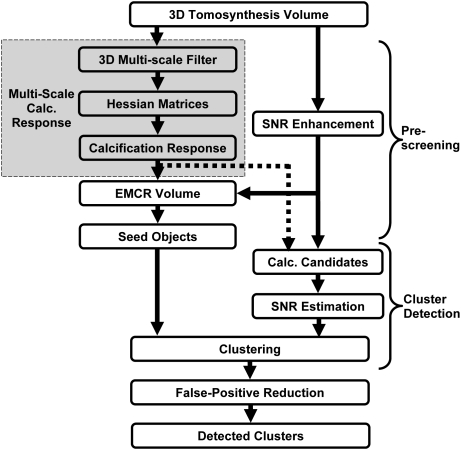
In this study, a prototype microcalcification cluster detection system was developed using a 3D approach in which the reconstructed 3D DBT volume was used as input. Figure 2 shows a block diagram of the CADe system, which consists of prescreening, cluster detection, and false-positive reduction stages. The details of each stage of the CADe system are described below.

Figure 2.

The block diagram of the microcalcification detection system for DBT.

Prescreening

In the prescreening stage, the microcalcifications are first enhanced using two parallel processes: One process is based on multiscale Hessian enhancement with a calcification response function, and the other is based on SNR enhancement of the microcalcifications in the reconstructed DBT volume. The calcification response volume resulting from Hessian enhancement is weighted by the SNR enhanced volume to obtain the enhancement-modulated calcification response (EMCR) at each voxel, and a maximum-gradient object growing and selection process is applied to the EMCR to identify seed objects for microcalcification clusters.

Multiscale calcification response

The multiscale Hessian enhancement method³⁴ is adapted to detect small bright objects with a spherical shape in DBT. It is based on the principle that at the center of a spherically symmetric object with positive contrast, the eigenvalues of the Hessian matrix are all negative and equal to each other. The Hessian matrix at voxels that are part of other kinds of shapes, such as lines or elongated ellipses, will have unequal eigenvalues. In practice, in order to tune the Hessian enhancement to objects at different scales and to reduce the noise that is amplified by the second-order derivatives in the Hessian operator, the image $\mathrm{I}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})$ is first convolved with a 3D Gaussian smoothing filter with scale σ

$${\mathrm{s}}_{\mathrm{\sigma }}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{=}\frac{1}{{(2\mathrm{\pi }{\mathrm{\sigma }}^2)}^{3\mathrm{/}2}}\exp \mathrm{\{}\mathrm{-}({\mathrm{x}}^2\mathrm{+}{\mathrm{y}}^2\mathrm{+}{\mathrm{z}}^2)\mathrm{/}2{\mathrm{\sigma }}^2\mathrm{\}}\mathrm{.}$$ (1)

Let $\mathrm{f}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})$ denote the smoothed image volume,

$${\mathrm{H}}_{\mathrm{\sigma }}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{=}\mathrm{\left[}\begin{array}{ccc}\multicolumn{1}{c}{{\mathrm{f}}_{\mathrm{xx}}}& \hfill {\mathrm{f}}_{\mathrm{xy}}\hfill & \hfill {\mathrm{f}}_{\mathrm{xz}}\hfill \\ \multicolumn{1}{c}{{\mathrm{f}}_{\mathrm{yx}}}& \hfill {\mathrm{f}}_{\mathrm{yy}}\hfill & \hfill {\mathrm{f}}_{\mathrm{yz}}\hfill \\ \multicolumn{1}{c}{{\mathrm{f}}_{\mathrm{zx}}}& \hfill {\mathrm{f}}_{\mathrm{zy}}\hfill & \hfill {\mathrm{f}}_{\mathrm{zz}}\hfill \end{array}\mathrm{\right]}\mathrm{,}$$ (2)

denote the Hessian matrix at a voxel (x,y,z) of the smoothed volume, and

$$\left|{\lambda }_3\right|\le \left|{\lambda }_2\right|\le \left|{\lambda }_1\right|,$$ (3)

denote the eigenvalues of the Hessian matrix at (x,y,z). One of the methods proposed in the literature³⁵ for enhancement of spherically symmetric object is to define a response $r_{\sigma }$ at scale σ as

$${\mathrm{r}}_{\mathrm{\sigma }}\mathrm{=}\mathrm{\{}\begin{array}{cc}\multicolumn{1}{c}{\mathrm{-}{\mathrm{\lambda }}_3^2\mathrm{/}{\mathrm{\lambda }}_1}& \hfill \mathrm{if}{\mathrm{\lambda }}_1\mathrm{\le }{\mathrm{\lambda }}_2\mathrm{\le }{\mathrm{\lambda }}_3\mathrm{\le }0\hfill \\ \multicolumn{1}{c}{0}& \hfill \mathrm{otherwise}\hfill \end{array}\mathrm{.}$$ (4)

If the object has a Gaussian shape with

$$\mathrm{I}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{=}\exp \mathrm{\{}\mathrm{-}({\mathrm{x}}^2\mathrm{+}{\mathrm{y}}^2\mathrm{+}{\mathrm{z}}^2)\mathrm{/}2{\mathrm{\sigma }}_0^2\mathrm{\}}\mathrm{,}$$ (5)

then it can be shown that among all possible scales for the filter ${\mathrm{s}}_{\mathrm{\sigma }}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})$, the scale

$$\sigma (=\sqrt{3/2}{\sigma }_0,$$ (6)

maximizes $r_{\sigma }$. In general, the size of the object is not known. A common approach in this case is to use a bank of Hessian filters $\mathrm{S}\mathrm{=}\mathrm{\{}{\mathrm{s}}_{{\mathrm{\sigma }}_1}\mathrm{,}{\mathrm{s}}_{{\mathrm{\sigma }}_2}\mathrm{,}\mathrm{\dots }\mathrm{,}{\mathrm{s}}_{{\mathrm{\sigma }}_{\mathrm{N}}}\mathrm{\}}$, at multiple scales $\{\sigma \}=\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_{\mathrm{N}}\}$. A response vector $R=\{r_{{\sigma }_1},r_{{\sigma }_2},\dots ,r_{{\sigma }_{\mathrm{N}}}\}$ is obtained at (x,y,z), and the elements of R are combined to achieve the desired signal enhancement. In a previous study on pulmonary nodule registration, we used a neural network to combine the elements of R.³⁶ In the current study, we first defined

$$\mathrm{i}\mathrm{*}\mathrm{=}\underset{\mathrm{i}}{\arg \text{max}}\mathrm{\left\{}{\mathrm{r}}_{{\mathrm{\sigma }}_{\mathrm{i}}}\mathrm{\right\}}\mathrm{.}$$ (7)

The multiscale calcification response at (x,y,z) was then defined as

$$\mathrm{E}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{=}\frac{{\mathrm{r}}_{{\mathrm{\sigma }}_{\mathrm{i}\mathrm{*}}}}{{\mathrm{\sigma }}_{\mathrm{i}\mathrm{*}}}\mathrm{.}$$ (8)

SNR enhancement

SNR enhancement was applied to each slice independently. It consisted of a combination of three filters, ${\mathrm{F}}_1$, ${\mathrm{F}}_2$, and ${\mathrm{F}}_3$, of sizes ${\mathrm{M}}_1\mathrm{\times }{\mathrm{M}}_1$, ${\mathrm{M}}_2\mathrm{\times }{\mathrm{M}}_2$, and ${\mathrm{M}}_3\mathrm{\times }{\mathrm{M}}_3$, respectively, where ${\mathrm{M}}_1\mathrm{>}{\mathrm{M}}_2\mathrm{\ge }{\mathrm{M}}_3$. The filters can be linear or nonlinear. If linear filters are chosen, the filters can be combined as follows to produce a single band-pass filter before convolution with the image to reduce processing time. The kernels of the filters are designed based on the following considerations. When the kernels are centered at the calcification candidate, a linear combination of the filters F₁ and F₂ is designed to obtain an estimate of the background image intensity around the calcification candidate. M₁ should be large enough to include the background, and M₂ large enough so that the microcalcification signal is excluded from the background estimation. The filter F₃ is used to estimate or increase the average signal intensity for the microcalcification candidate, depending on the selection of M₃. In this study, for simplicity, we chose to use boxcar filters for F₁, F₂, and F₃, where the kernel weights of the filter F_i is $1/{\mathrm{M}}_{\mathrm{i}}^2$ in an ${\mathrm{M}}_{\mathrm{i}}\mathrm{\times }{\mathrm{M}}_{\mathrm{i}}$ box, and 0 elsewhere. Other filters such as Gaussian filters with appropriate kernels can be used as well. SNR enhancement was accomplished by convolving the combined band-pass filter with the DBT volume

$$\begin{array}{c}\multicolumn{1}{c}{\mathrm{F}(\mathrm{x}\mathrm{,}\mathrm{y})\mathrm{=}{\mathrm{F}}_3(\mathrm{x}\mathrm{,}\mathrm{y})\mathrm{-}\frac{1}{{\mathrm{M}}_1^2\mathrm{-}{\mathrm{M}}_2^2}\mathrm{\times }\mathrm{[}{\mathrm{M}}_1^2{\mathrm{F}}_1(\mathrm{x}\mathrm{,}\mathrm{y})\mathrm{-}{\mathrm{M}}_2^2{\mathrm{F}}_2(\mathrm{x}\mathrm{,}\mathrm{y})\mathrm{]}\mathrm{.}}\end{array}$$ (9)

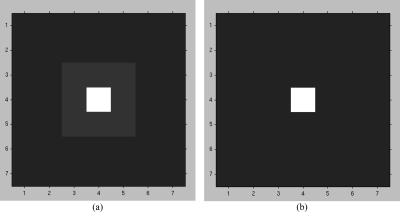
Examples of the enhancement filter for different values of M₁, M₂, and M₃ are shown in Fig. 3.

Figure 3.

The filter F used for SNR enhancement. (a) M₁ = 7, M₂ = 3, M₃ = 1. The white, light gray, and dark gray parts of the image representing the filter kernel have weights of 1, 0, and −1/40, respectively. (b) M₁ = 7, M₂ = 1, M₃ = 1. The white and dark gray parts of the image representing the filter kernel have weights of 1 and −1/48, respectively. The pixel size of the filter kernel was 0.1 mm × 0.1 mm.

Cluster seed object detection

The EMCR volume was defined as the voxel-by-voxel weighting of the multiscale calcification response volume by the SNR-enhanced volume

$$\mathrm{EMCR}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{=}\mathrm{E}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{*}\mathrm{[}\mathrm{I}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{\otimes }\mathrm{F}(\mathrm{x}\mathrm{,}\mathrm{y})\mathrm{]}\mathrm{,}$$ (10)

where $\mathrm{I}(\mathrm{x}\mathrm{,}\mathrm{y}\mathrm{,}\mathrm{z})\mathrm{\otimes }\mathrm{F}(\mathrm{x}\mathrm{,}\mathrm{y})$ denotes the SNR-enhanced volume. Since both multiscale calcification response and SNR-enhancement are intended to make the microcalcifications more discernable, their product may also be expected to improve microcalcification detection. Although other methods can be used to fuse these two images (including supervised methods), we did not investigate other potential methods in this feasibility study.

Figure 4a shows a slice of a DBT volume containing a microcalcification cluster that was biopsy-proven to be ductal carcinoma in situ. Figures 4b, 4c, 4d show the SNR-enhanced image, multiscale calcification response image, and EMCR image, respectively, corresponding to the same slice.

Figure 4.

(a) A DBT slice containing a small microcalcification cluster, (b) The SNR-enhanced image, (c) The calcification response image, and (d) The EMCR image of the same slice.

In the EMCR volume, an iterative thresholding and object growing technique was designed to detect at least 500 initial objects. The technique started with an initial threshold. Voxels that were above the initial threshold were marked and grouped into 3D connected objects using 26-connectivity.³⁷ The initial threshold was chosen to be relatively high so that only a few connected objects would be initially detected. The threshold was then iteratively decreased until the number of connected objects was at least 500. For each detected initial object, the voxel with the highest EMCR value was defined as the initial seed point.

In the early stage of development, it was found that these initial objects included small, noncalcified densities in the image. The sizes of these densities were larger than those of most microcalcifications, and the transition from the density to the background was smoother than that for microcalcifications. To eliminate some of these noncalcified densities, we first segmented all initial objects in the original image volume using a maximum-gradient object growing method.²⁸ Starting with the initial seed point, the object was segmented in a local region of the original DBT reconstruction volume using a multiple thresholding technique. The local region was selected as a 2.1 mm 2.1 mm box centered at the initial seed point. The maximum threshold was chosen to be the largest voxel value in the local 3D region. The threshold was lowered from this maximum value in multiple equal-sized steps of 16 gray levels. At each threshold value, the connected object grown around the initial seed point was extracted, and the average radial gradient magnitude around the object resulting from the particular threshold was calculated. The object with the highest average radial gradient magnitude was retained as the final segmented object. Objects with a volume larger than a predefined threshold Vol_max(Vol_max = 0.25 mm³) were eliminated. The remaining objects are referred to as cluster seed objects below.

Cluster detection

For cluster detection, we first located individual microcalcification candidates, independent of the cluster seed object detection, described in Sec. 2B1c above. To detect the microcalcification candidates, we applied a second iterative thresholding and object growing procedure, which was similar to that described above except that it was applied to the SNR-enhanced volume. In the object growing process, any voxel that had a zero value for the multiscale calcification response volume [refer to Eqs. 4, 8] was excluded. The threshold was reduced iteratively until at least 5000 objects, referred to as individual microcalcification candidates below, were detected in the DBT volume. The final threshold determined above was termed the global object detection threshold.

The SNR around each individual microcalcification candidate was estimated using the SNR-enhanced volume as follows: All voxel grayscale values referred to in this step were values in the SNR-enhanced volume. Let Loc_max denote the (x,y,z) location of the voxel with the highest grayscale value within a segmented microcalcification candidate. The background region around Loc_max was defined as a $5\times 5\times 5\mathrm{mm}$ cube centered at Loc_max with voxels that had values less than the global object detection threshold. The average of the background voxels was calculated and subtracted from the grayscale value at Loc_max to define the signal level. The SNR of the microcalcification candidate was then found as the ratio of the signal level to the standard deviation of the background voxels. The segmentation of the microcalcification candidate centered at Loc_max was refined by extracting voxels that had an SNR greater than a selected threshold and were connected by 26-connectivity. An SNR threshold of 3.0 was chosen for including a voxel in the microcalcification candidate. The final size of the microcalcification candidate was estimated from the SNR-segmented object.

After the set of cluster seed objects and the set of individual microcalcification candidates were detected, as described above, a dynamic clustering process was used to detect cluster candidates as follows. Note that although at least 5000 individual microcalcification candidates were detected, clustering was performed only around the cluster seed objects. Starting with a cluster seed object as the initial cluster center, individual microcalcification candidates that satisfied the membership criteria below were included as cluster members one at a time. Microcalcification candidates were ranked with respect to their SNR and were sequentially included as members of the cluster candidate following their rank order if their SNR exceeded an SNR threshold, chosen as 3.0 in this study, and if they were within a 5 mm radius of the cluster center. These parameters were chosen based on our experience in microcalcification detection on mammograms^38∓40 and further experiments with DBT. After the inclusion of each new microcalcification candidate, the cluster center was updated as the centroid of all individual microcalcification locations included in the cluster. The SNR of the cluster was also updated as the highest SNR among the individual microcalcifications within the cluster. Individual microcalcification candidates that were included into a given cluster were marked and were excluded from being a candidate member of other clusters.

False-positive reduction

We used a rule-based classifier with three rules related to the size, SNR, and the number of individual microcalcifications within a candidate cluster for false-positive reduction. First, we counted the number of individual microcalcification candidates within a cluster candidate with an SNR of 3.5 or more. The first rule specified that if this number was less than 4, the cluster candidate would be eliminated. Second, we counted the number of individual microcalcification candidates with a size of seven voxels or more within a cluster candidate. As described above, an SNR threshold of 3.0 was used as a region-growing criterion to find the individual microcalcification size. The second rule specified that if this number was less than 4, the cluster candidate would be eliminated, unless the third rule, described below, was satisfied. As an example, according to the second rule, if a cluster candidate had eight microcalcification candidates, but only three of them had a size larger than or equal to 7, the cluster candidate was eliminated. This rule was therefore aimed at eliminating FP clusters with small objects that are presumably caused by image noise. However, some true clusters may consist of a large number of tiny microcalcifications. In order not to eliminate these clusters, the third rule specified that cluster candidates with ten or more members should be kept, regardless of the individual object sizes and their SNRs.

The bounding boxes of the clusters were also examined for false-positive reduction. The width and height of the cluster were defined as the two dimensions of the bounding box in the plane parallel to the detector, while the depth was defined as that in the perpendicular direction. A width or height less than 2 mm, and a rectangularity >3, where rectangularity is defined as the ratio of the larger dimension to smaller dimension, was considered to be an indication of a linear artifact, and such cluster candidates would be eliminated.

Performance evaluation

In order to select parameters for prescreening, we performed a number of experiments. The prescreening performance was estimated using only the abnormal data set of 144 DBT scans that contained microcalcification clusters. The normal data set was not used at this stage. At this early phase of design, we used a simple method to plot a curve similar to a free-response receiver operating characteristic (FROC) curve to evaluate the performance of the prescreening stage. First, we defined the score of each object as the highest EMCR value within the object. Next, we ranked the objects within the DBT volume according to their scores. Finally, we determined what fraction F of DBT volumes would have a correctly localized cluster if we only kept R highest-scoring objects per volume. As an example, assume that each DBT volume contained one true cluster, V₀ out of a total of V volumes had the true cluster as the highest ranking object, and V₁ different volumes had the true cluster as the second-highest ranking object. Then one would have $\mathcal{F}(\mathcal{R}=1)={\mathrm{V}}_0/\mathrm{V}$, and $\mathcal{F}(\mathcal{R}=2)=({\mathrm{V}}_0+{\mathrm{V}}_1)/\mathrm{V}$. The resulting plot of (R, F) pairs is referred to as a rank-sensitivity plot below. At a given operating point defined by the number of retained objects ${\mathcal{R}}_0$₀, the rank-sensitivity plot indicates that F(R₀)*V true clusters were detected in the data set. However, this is a minimum number in terms of TP objects because some clusters may be detected as multiple objects. Since the total number of computer marks at this operating point is R₀*V, the average number of FPs per image unit at this operating point is at most (R₀ - F(R₀))*V.

After parameter selection, the overall performance of the detection system, including clustering and FP reduction, was evaluated using FROC analysis. For this purpose, the highest SNR value among the objects within a detected cluster was defined as the SNR of the cluster and used as the decision variable. The detected cluster was considered to be a true-positive if its centroid was within the 3D ground-truth box determined by the radiologist. Otherwise, the detected cluster was considered a false-positive. Separate FROC curves were constructed for malignant, benign, and all calcification clusters for comparison. We separately used the normal data set of 76 DBT volumes, and the abnormal data set of 144 DBT volumes to estimate the average number of FPs at each SNR threshold. FPs estimated from these two data sets were used to plot two sets of FROC curves.

RESULTS

Effect of the Hessian response function parameters

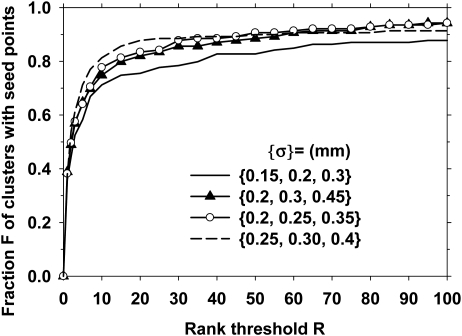
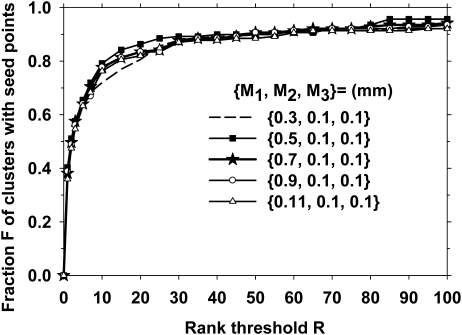
As discussed above, a bank of Gaussian filters S corresponding to a set of N scales $\{\sigma \}=\{{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_{\mathrm{N}}\}$ was used for multiscale Hessian response function. We evaluated the effect of the scales on the calcification response. A small number of scales, N = 3, was used to keep the computational cost low. The scale of the Gaussian filter was varied between $\sigma =0.15\mathrm{mm}$ and $0.45\mathrm{mm}$, with various combinations of the scales to constitute the bank of filters S. In this part of the investigation, the SNR enhancement filter was fixed at ${\mathrm{M}}_1=0.7\mathrm{mm}$, ${\mathrm{M}}_2=0.1\mathrm{mm}$, and ${\mathrm{M}}_3=0.1\mathrm{mm}$. The rank-sensitivity plots are shown in Fig. 5. Based on these results, the set of scales was selected as $\left\{\sigma \right\}=\left\{0.2\text{\hspace{0.17em}mm},0.25\text{\hspace{0.17em}mm},0.35\text{\hspace{0.17em}mm}\right\}$ because it could reach the highest sensitivity (with lax rank threshold) at this prescreening stage.

Figure 5.

The effect of the size of the Hessian multiscale filters on the prescreening performance. The plot shows the fraction of true clusters in the data set that included a cluster seed object as a function of the rank of the objects that were retained per DBT volume. In this part of the investigation, the SNR enhancement filter kernels were fixed at ${\mathrm{M}}_1=0.7$ mm, ${\mathrm{M}}_2=0.1$ mm, and ${\mathrm{M}}_3=0.1$ mm.

Effect of the SNR enhancement filter parameters

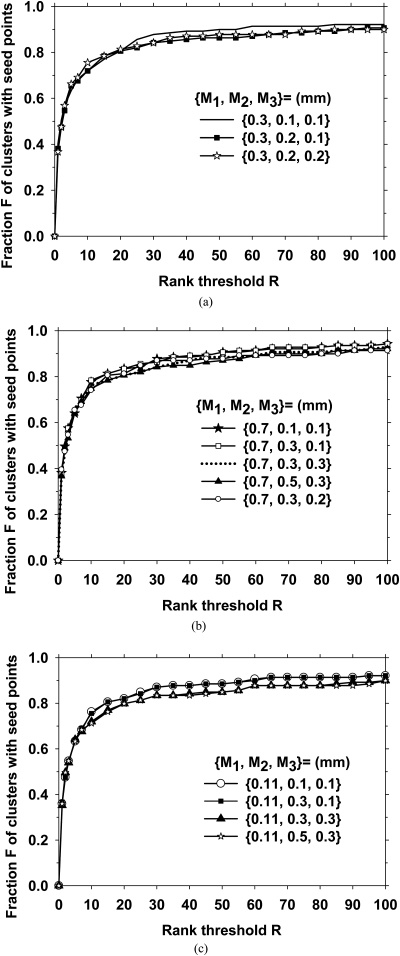
To investigate the effect of SNR enhancement filter parameters, we first changed ${\mathrm{M}}_1$ in the range of 0.3 mm to 1.1 mm. In this part of the investigation, we fixed the other two filters to be ${\mathrm{M}}_2={\mathrm{M}}_3=0.1$ mm, and the Hessian multiscale filters at $\{\sigma \}=\{0.20\mathrm{mm}\mathrm{,}0\mathrm{.}25\mathrm{mm}\mathrm{,}0\mathrm{.}35\mathrm{mm}\}$. The resulting rank-sensitivity plots are shown in Fig. 6. It is observed that a small background area, M₁ = 0.3, resulted in a slightly poorer performance, while the other values of ${\mathrm{M}}_1$ led to comparable rank-sensitivity curves. We then studied the effect of ${\mathrm{M}}_2$ and ${\mathrm{M}}_3$. Figures 7a, 7b, 7c show the effects of varying ${\mathrm{M}}_2$ and ${\mathrm{M}}_3$ for ${\mathrm{M}}_1=$ 0.3, 0.7, and 0.11 mm, respectively. Because the seed object detection appeared to be relatively stable for M₁ from 0.7 to 1.1 mm, we selected ${\mathrm{M}}_1=0.7$ mm, ${\mathrm{M}}_2=0.1$ mm, and ${\mathrm{M}}_3=0.1$ mm for the SNR enhancement. As shown in Fig. 7b, at an operating point of rank threshold of 100, which was equivalent to a threshold of keeping 100 cluster seed objects per DBT volume, 94% of biopsied calcification clusters contained a seed object.

Figure 6.

The effect of the size of the outer filter kernel (${\mathrm{M}}_1$) on the prescreening performance. The inner filter kernel sizes were selected as ${\mathrm{M}}_2={\mathrm{M}}_3=0.1$ mm, and the Hessian multiscale filters were fixed at $\{\sigma \}=\{0.20\mathrm{mm}\mathrm{,}0\mathrm{.}25\mathrm{mm}\mathrm{,}0\mathrm{.}35\mathrm{mm}\}$

Figure 7.

The effect of the sizes of the inner filter kernels (M₂ and M₃) on the prescreening performance. The Hessian multiscale filters were fixed at {σ} = {0.20 mm, 0.25 mm, 0.35 mm}. The outer filter kernel M₁ was set to be 0.3, 0.7, and 0.11 mm in Figs. 7(a)–7(c), respectively.

Effect of enhancement modulated calcification response

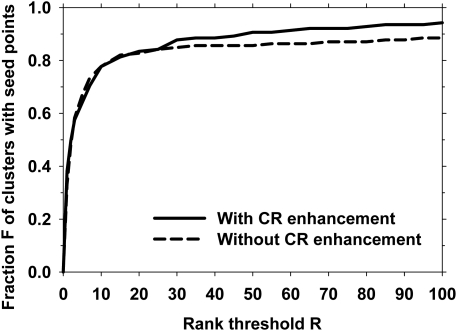
We investigated the effect of modulating the multiscale calcification response with the SNR-enhanced image. We compared the prescreening rank-sensitivity plot with the calcification response function in place ($\left\{\sigma \right\}=\left\{0.20\text{\hspace{0.17em}mm},0.25\text{\hspace{0.17em}mm},0.35\text{\hspace{0.17em}mm}\right\}$) to that when the output of the multiscale calcification response (see Fig. 2) was replaced by a spatially constant value over the DBT volume. This was equivalent to removing the multiscale calcification response enhancement and using only SNR-enhancement during prescreening. The parameters of the SNR enhancement filter were ${\mathrm{M}}_1=0.7$ mm, ${\mathrm{M}}_2=0.1$ mm, and ${\mathrm{M}}_3=0.1$ mm, as discussed above. Figure 8 shows a comparison of the two prescreening approaches.

Figure 8.

Rank-sensitivity plots for the prescreening performance with and without the multiscale calcification response (CR) enhancement.

Effect of clustering and false-positive reduction

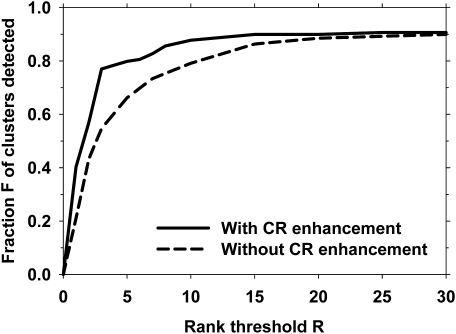
The next step in our detection system was clustering. We first compared the rank-sensitivity plots with and without the multiscale calcification response in Fig. 9. At this stage, the cluster SNR (i.e., the highest SNR value of the microcalcification candidates within a cluster) was available, as described in Sec. 2B2 above. Similar to the final FROC curves described below, we used the cluster SNR as the decision variable, since the unit of interest at this stage was the cluster, instead of the cluster seed objects as in Figs. 5678. Figure 9 is similar to Fig. 8 except that the cluster SNR was used as the decision variable for ranking. At an operating point of ten clusters per DBT volume, 88% and 79% of the true calcification clusters could be correctly identified with and without the multiscale calcification response, respectively. The rank-sensitivity curve after clustering was higher than those before clustering (Figs. 5678) because the clustering process eliminated some of the false positives. A comparison of the sensitivity of the system at different rank thresholds before and after clustering is shown in Table TABLE I..

Figure 9.

Rank-sensitivity plots for the performance after the clustering stage with and without the multiscale CR enhancement.

Table 1.

A comparison of the sensitivity of the system at different rank thresholds before and after clustering (also compare solid lines in Figs. 89). The filter parameters were $\{\sigma \}=\{0.2\mathrm{mm}\mathrm{,}0\mathrm{.}25\mathrm{mm}\mathrm{,}0\mathrm{.}35\mathrm{mm}\}$ and (${\mathrm{M}}_1$, ${\mathrm{M}}_2$, ${\mathrm{M}}_3$) = (0.7 mm, 0.1 mm, 0.1 mm).

Rank threshold	1	2	3	5	10	20	30
Sensitivity before clustering	0.38	0.50	0.58	0.64	0.78	0.83	0.88
Sensitivity after clustering	0.40	0.57	0.77	0.80	0.88	0.90	0.91

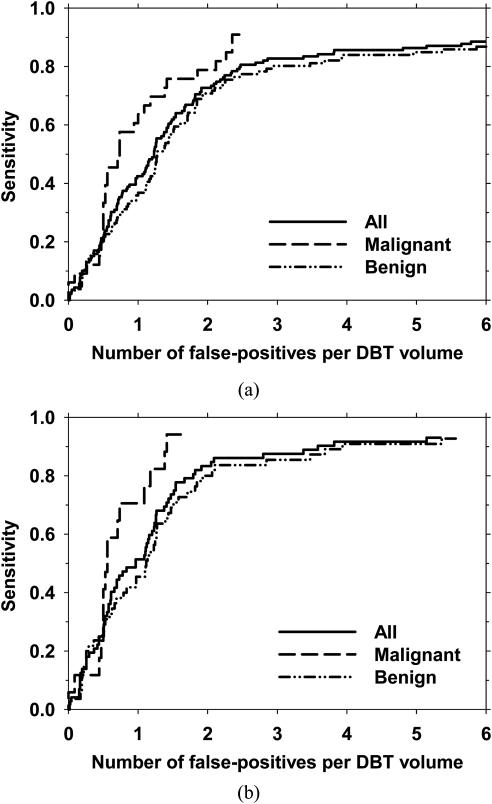
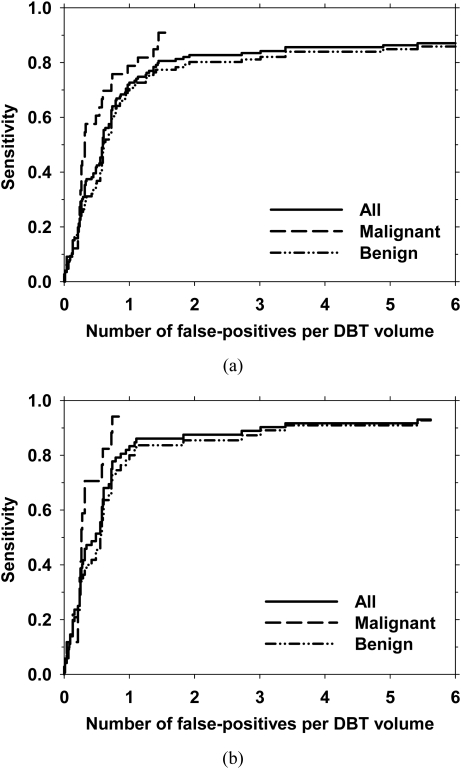
The final FROC curves for the detection system, with the FP rate estimated from the abnormal data set after false-positive reduction, are shown in Figs. 10a, 10b for view-based and case-based scoring, respectively. In view-based scoring, the same cluster seen in the CC and MLO views was counted independently such that the total number of true clusters was 139. In case-based scoring, a cluster was considered to be detected if its score exceeded the decision threshold in either one or both of the CC and MLO views and the total number of true clusters were 72. The FROC curves for view-based and case-based scoring with the average FP rates estimated from the normal data set are shown in Figs. 11a, 11b, respectively. Using view-based scoring, at 85% sensitivity, the average number of FPs estimated using the abnormal and normal data sets were 3.8 and 3.4 per DBT volume, respectively. The FP rates estimated using the two data sets at these sensitivity levels for both scoring methods for the entire data set, the malignant subset, and the benign subset are shown in Table TABLE II..

Figure 10.

The overall performance of the microcalcification detection system in terms of the FROC curves for all clusters, and the subsets of malignant clusters and benign clusters. The average number of false-positives per DBT volume was estimated using the abnormal data set. (a) view-based and (b) case-based detection performance. In case-based detection, a cluster was considered to be detected if the cluster was detected on either one or both views.

Figure 11.

The overall performance of the microcalcification detection system in terms of the FROC curves for all clusters, and the subsets of malignant clusters and benign clusters. The average number of false-positives per DBT volume was estimated using the normal data set. (a) view-based and (b) case-based detection performance. In case-based detection, a cluster was considered to be detected if the cluster was detected on either one or both views.

Table 2.

Average number of false-positives per reconstructed DBT volume at a sensitivity of 80% and 85%. For each level of sensitivity, the number of false-positives estimated from abnormal cases (i.e., cases containing microcalcification clusters) and estimated from normal cases (i.e., cases free of microcalcification clusters) are listed in columns labeled “Abnorm” and “Norm,” respectively.

	80% sensitivity (view-based)		85% sensitivity (view-based)		80% sensitivity (case-based)		85% sensitivity (case-based)
Clusters	Abnorm	Norm	Abnorm	Norm	Abnorm	Norm	Abnorm	Norm
All	2.5	1.4	3.8	3.4	1.8	0.9	2.1	1.1
Malignant	2.1	1.1	2.4	1.4	1.2	0.6	1.4	0.7
Benign	2.9	1.9	5.4	5.4	1.9	1.1	3.5	1.8

DISCUSSION

Our results indicate the feasibility of automated detection of microcalcification clusters in reconstructed DBT volumes using our new enhancement-modulated 3D calcification response approach. This approach utilized the combination of two calcification enhancement processes: (1) enhancement of calcification response based on Hessian analysis and (2) SNR enhancement based on a combination of filters. The SNR enhancement technique may be effective in highlighting small, high-contrast objects, as demonstrated by the example image in Fig. 4. However, it also enhances line-type structures, which may result in FP detections or FNs in the prescreening stage that may propagate to other stages of the detection process. Figures 89 show that the combination of the two enhancement processes resulted in an improved performance compared to SNR enhancement alone.

The calcification response derived from multiscale Gaussian filters with the smallest widths ($\left\{\sigma \right\}=\left\{0.15\text{\hspace{0.17em}mm},0.20\text{\hspace{0.17em}mm},0.30\text{\hspace{0.17em}mm}\right\}$) had a lower rank-sensitivity plot than the other filter sets, as shown in Fig. 5. This may indicate that if a cluster included at least one larger microcalcification to provide a seed point, the chance of detecting that cluster would be higher. For SNR enhancement, the size of the outer box used for background estimation, ${\mathrm{M}}_1$, did not have a major effect on the prescreening performance, as shown in Fig. 6, when it was 0.5 mm or larger. Because most microcalcifications of interest were smaller than 0.5 mm, this result was consistent with the expectation that the background should be estimated in a small region surrounding the microcalcification without including the calcification itself. The prescreening performance was slightly degraded when the inner box sizes were increased from (${\mathrm{M}}_2$, ${\mathrm{M}}_3$) = (0.1 mm, 0.1 mm), as shown if Fig. 7. The final choice of (${\mathrm{M}}_1$, ${\mathrm{M}}_2$, ${\mathrm{M}}_3$) = (0.7 mm, 0.1 mm, 0.1 mm) showed that the reconstructed DBT slices were relatively smooth so that no additional smoothing was needed to achieve the best SNR for our data set.

The FP rate estimated from the abnormal data set was higher than that estimated from the normal data set (Table TABLE II.). To investigate the cause of the difference in the FP rates, the reference radiologist inspected each of the 832 FP marks (5.8 FPs/DBT volume) produced by the CAD system for the abnormal data set at the highest sensitivity level in Fig. 10 (sensitivity = 88%). A similar inspection was also performed for the normal data set. The results indicated that an average of 1.8 FP marks per DBT volume in the abnormal data set contained individual microcalcifications that were not considered clustered, while the normal data set contained an average of 0.7 such FP marks per DBT volume. It therefore appears that the abnormal cases more likely contained scattered microcalcifications that were not considered clinically significant clusters. However, when they were combined with microcalcification candidates caused by image noise, these microcalcifications increased the likelihood of producing FP clusters, resulting in the higher FP rates estimated from the abnormal data set.

Similar to previous results for the detection of microcalcification clusters on mammograms,⁴¹ the detection performance for malignant clusters in this work was superior to that for benign clusters. For malignant clusters, a case-based sensitivity of 80% was obtained at about 1.2 FP per DBT volume, while the FP rate was about 1.9 for benign clusters at the same sensitivity. However, the number of malignant cases in this work was relatively low (17 of 72), which may limit the generalizability of this result. Due to the small data set size for both malignant and benign clusters in this preliminary study, independent testing was not performed for the detection system. Although the performance in the prescreening stage was not very sensitive to filter parameters within the studied range, and the FP reduction stage included simple rule-based decision criteria to reduce overtraining, our results may be optimistically biased due to the lack of independent testing. Future study with independent training and test sets is required to assess the generalizability of our detection system.

The processing parameters used in prescreening may depend on the reconstruction algorithm. The DBT volumes in this study were reconstructed using the SART algorithm. Other techniques, such as filtered-backprojection or maximum-likelihood reconstruction methods may produce DBT with different noise and signal properties. Likewise, the relaxation parameter, number of iterations, and the access order to the PVs in SART reconstruction may affect the reconstructed images. The effect of the reconstruction algorithm and parameters on the detection performance, and whether the techniques and parameters in the detection system need to be redesigned to adapt to different quality of DBT images are topics for further investigation.

Our CAD system contained a large number of parameters for presecreening, clustering, and FP reduction stages. In this preliminary study, we focused on the effect of the filter parameters for the multiscale calcification response and SNR enhancement. The choices of other parameters, such as the $\mathit{Vo}{l}_{\text{max}}$ threshold, the minimum number of cluster seed objects detected in the EMCR volume, and the minimum number of microcalcification candidates detected in the SNR-enhanced volume, were based on initial experience rather than systematic investigations. Further studies with a larger database to optimize these and other processing parameters have a potential to improve the microcalcification detection performance.

The calcification response function used in this study was designed for spherically symmetric objects. True microcalcifications will have a variety of shapes, including oblong and irregular. In addition, the interplane artifacts from the reconstruction algorithm will distort the shape of the microcalcifications in the depth direction. The design of the parameters in this preliminary study did not take into consideration the anisotropic properties of the signal and the noise. Accurate modeling of the electronic, quantum, and structured noise components, the microcalcification signal, and the artifacts introduced by the limited-angle reconstruction and studies of their effects on detection performance will be interesting topics of future investigation.

This study investigated the detection of microcalcification clusters only in the reconstructed DBT volumes, while some other studies have investigated microcalcification detection on PVs.^{30, 32} These two approaches may have different strengths. Detection on PVs may leverage existing detection algorithms on mammograms and does not depend on specific reconstruction method. However, due to the low SNR on each PV, some of the parameters in the existing detection algorithms on mammograms will require adjustment. It is generally accepted that preprocessing is one of the key components of a CADe algorithm. Tomosynthesis reconstruction can be considered to be a preprocessing step in the 3D detection approach, which combines the information from the multiple PVs and increases the SNR of the targets. We have previously demonstrated that fusion of information from mass candidates detected in the 3D volume and those detected in the 2D PVs can improve the detection accuracy compared to the individual approaches.²⁸ The usefulness of such strategy should be investigated for microcalcification detection in future studies.

CONCLUSION

We have investigated the feasibility of developing a CADe system for detection of microcalcification clusters in reconstructed DBT volumes. The results indicate that our new enhancement-modulated 3D calcification response method is a promising approach although the current false-positive rate is too high to be acceptable in clinical practice. Future work includes further optimization of the machine vision techniques and parameters using a large training set and evaluation using an independent test set, the combination of 2D detection on PVs with 3D detection in the reconstructed volume, study of the effects of reconstruction technique and parameters on detection accuracy, and comparison of microcalcification detection in DBT and in corresponding mammograms. Further improvement in detection accuracy is needed before observer performance studies can be conducted to evaluate whether the CADe system may be useful as a second reader to assist radiologists in detection of clustered microcalcifications in DBT.