Abstract
Free recall is a fundamental paradigm for studying memory retrieval in the context of minimal cue support. Accordingly, free recall has been extensively studied using behavioral methods. However, the neural mechanisms that support free recall have not been fully investigated due to technical challenges associated with probing individual recall events with neuroimaging methods. Of particular concern is the extent to which the uncontrolled latencies associated with recall events can confer sufficient design efficiency to permit neural activation for individual conditions to be distinguished. The present study sought to rigorously assess the feasibility of testing individual free recall events with fMRI. We used both theoretically and empirically derived free recall latency distributions to generate simulated fMRI data sets and assessed design efficiency across a range of parameters that describe free recall performance and fMRI designs. In addition, two fMRI experiments empirically assessed whether differential neural activation in visual cortex at onsets determined by true free recall performance across different conditions can be resolved. Collectively, these results specify the design and performance parameters that can provide comparable efficiency between free recall designs and more traditional jittered event-related designs. These findings suggest that assessing BOLD response during free recall using fMRI is feasible, under certain conditions, and can serve as a powerful tool in understanding the neural bases of memory search and overt retrieval.
INTRODUCTION
In free recall, participants are presented with a study list, and are asked to remember as many studied items as possible from the list, in any order they choose. Thus, free recall is an exemplary test of controlled memory search, as it requires guiding retrieval in a goal-directed manner in the context of minimal external cue support. Indeed, free recall has been the focus of considerable behavioral experimentation in the cognitive psychology literature, and has provided core data on which many classic computational models of memory are based (e.g., Gillund & Shiffrin, 1984; Raaijmakers & Shiffrin, 1981; Anderson & Bower, 1972).
Despite being a fundamental memory paradigm and benefiting from extensive behavioral research, the neural mechanisms that support free recall have not been as thoroughly investigated. Early studies using PET measured activation during blocks of free recall (e.g., Petersson, Sanblom, Gisselgard, & Ingvar, 2001; Ricker et al., 2001; Andreasen et al., 1995a, 1995b). However, given the low temporal resolution of the PET methodology, such studies were limited in their ability to distinguish individual trial types. Current fMRI methods are capable of distinguishing individual events. However, for reasons discussed below, the application of event-related fMRI methodology to free recall has been highly limited, being restricted almost entirely to investigations of neural activation during encoding that predicts subsequent free recall (e.g., Dickerson et al., 2007; Staresina & Davachi, 2006). To date, the only fMRI study to focus on recall assessed distributed neural activation during free recall using a pattern classifier analysis. This analysis identified patterns of neural activation at encoding that were reinstated later during the free recall period (Polyn, Natu, Cohen, & Norman, 2005). However, the neural systems that support individual free recall conditions have not been investigated with traditional event-related fMRI, which has significant advantages over blocked designs. First, with event-related designs, it is possible to estimate neural activation for mixed individual trial types. Second, event-related designs have the advantage of conducting analyses depending on the participant’s success. Third, event-related designs can also eliminate strategy effects that may occur in blocked designs. Most notably, the ability to have an event-related design in the context of free recall would enable the researchers to estimate differential neural activation across different free recall conditions, and further examine neural activation modulated by participant’s success or other behavioral characteristics.
There are three major technical obstacles to studying free recall in fMRI: (1) Movement artifacts can be induced in a trial-correlated manner when people speak during fMRI scanning; (2) recording voice responses can be difficult in the context of a noisy fMRI pulse sequence; and (3) uncontrolled recall latencies make individual recall events difficult to distinguish given the sluggish nature of the blood oxygenation level dependent (BOLD) response. The first two of these issues related to speaking in the magnet raise challenges but are surmountable when a verbal response is necessary. Barch et al. (1999) have shown that movement-related artifacts during speaking are not as prevalent as would be expected, and that using group data largely overcomes movement artifacts present in individual participants’ data. In addition, problems associated with concurrent scanner noise during an EPI scan can be overcome with the use of appropriate noise canceling algorithms (e.g., Cusack, Cumming, Bor, Norris, & Lyzenga, 2005).
Accordingly, the primary obstacle to studying free recall with fMRI is the lack of experimental control over recall latencies of individual items. We note that although unconstrained recall is a component of memory tasks outside of list recall, such as autobiographical memory retrieval, list recall is particularly problematic because it does not necessarily permit the temporal isolation of individual events necessary for fMRI analysis. In statistical terms, this lack of control poses a threat to design efficiency. As a consequence, studying free recall with event-related fMRI is widely assumed to be infeasible.
Efficiency of a design refers to its ability to detect and estimate neural activation for its particular experimental variables of interest. Design efficiency in fMRI can refer to the ability to detect a significant response (i.e., detection power), or the ability to estimate the shape of the response (i.e., estimation efficiency) (e.g., Henson, 2004; Liu & Frank, 2004). In typical fMRI designs, several variables affect estimation efficiency and some of these can be manipulated a priori to optimize efficiency (e.g., Wager & Nichols, 2003; Ollinger, Corbetta, & Shulman, 2001; Ollinger, Shulman, & Corbetta, 2001; Dale, 1999). For example, efficiency will be increased by maximizing the conditional entropy through nth-order counterbalancing of the trial order of experimental conditions. Likewise, efficiency can be improved via introducing jittered null intervals in between experimental trials (intertrial intervals) to ensure that the BOLD response pertaining to each individual cognitive or sensory event can be resolved with a unique solution based on the data (see Liu, Frank, Wong, & Buxton, 2001, and Donaldson & Buckner, 2000, for an overview of effective fMRI designs).
In the case of free recall, efficiency becomes problematic due to a lack of experimental control over condition ordering, and consequently, no control over conditional entropy. Moreover, subject-determined recall latencies prohibit any control over trial onsets or the intertrial interval. As a further complication, the neural signal and the consequent BOLD response will be affected by the characteristics of the retrieval process that the participant is engaging in, which is likely ongoing throughout the interval between each recall event. Without such control and the ability to optimize efficiency, it has been unclear whether it would be possible to detect and estimate neural activation for individual free recall events with fMRI. However, recall latencies are usually not random nor do they occur at fixed frequencies. Thus, despite the above intuitions, it has not been formally investigated to what extent free recall prohibits event-related analysis because free recall events do not convey sufficient efficiency. In what follows, we more formally introduce the statistical definition of efficiency and the nature of free recall distributions.
Efficiency
The efficiency of a design can refer to its detection power or its estimation efficiency (Liu, 2004). Detection power refers to the ability to detect a difference in amplitude of neural activation using a canonical hemodynamic response function (HRF). Estimation efficiency refers to the ability to characterize the shape of the HRF (e.g., Henson, 2004; Liu et al., 2001). It can be demonstrated that detection power and estimation efficiency trade off (Liu & Frank, 2004). Thus, blocked designs typically have higher detection power compared to event-related designs. Conversely, event-related designs typically have higher estimation efficiency than blocked designs (see Henson, 2004 for illustration).
Efficiency can be computed for a given contrast of interest from an fMRI design using the following equation (Henson, 2004; Liu et al., 2001; Dale, 1999; Friston, Zarahn, Josephs, Henson, & Dale, 1999)
| (1) |
In Equation 1, E is the estimated design efficiency, X is the design matrix, and C is the particular contrast of interest. E is inversely related to the covariance of the regressors in the design matrix X. Note that E has no units and is a relative measure that can be used to compare different designs, without providing an absolute magnitude comparison. This equation can be used to evaluate both detection power and estimation efficiency—by using either an assumed HRF or a finite impulse response function, respectively (Henson, 2004). In this article, we use Equation 1 to evaluate detection power across event-related conditions, using a canonical HRF. However, in Experiments 1 and 2, we also evaluate estimation efficiency.
Dynamics of Free Recall
Free recall has been extensively studied in behavioral research, and the properties of free recall latency distributions are well known (e.g., Rohrer & Wixted, 1994; Wixted & Rohrer, 1994). Latency distributions originating from free recall data as a function of time (t) typically follow an ex-Gaussian distribution (Equation 2) that is derived from a Gaussian convolved with an exponential (Rohrer & Wixted, 1994; Wixted & Rohrer, 1993, 1994; Burbeck & Luce, 1982; Ratcliff, 1979).
| (2) |
The ex-Gaussian distribution emerges when response latencies reflect the contribution of two distinct stages, a normally distributed stage (i.e., Gaussian) and an exponentially distributed stage (Rohrer & Wixted, 1994). In the case of free recall latencies, the Gaussian stage presumably corresponds to the initiation period that precedes the recall of the first item. This stage can be described by parameters μ (mu) and σ (sigma). The exponential stage, which is the critical stage for our purposes, reflects the ongoing search in memory for studied items that recovers items at a rate that declines exponentially. This stage can be described by one parameter, τ (tau) (see Rohrer & Wixted, 1994 for a detailed overview).
Current Study
In this article, we investigate whether it is feasible to study free recall with a traditional event-related fMRI design. Specifically, we seek to identify the boundary conditions under which estimation efficiency is optimal during free recall. We report a set of simulations and experiments that varies the parameters that determine design efficiency and free recall latency distributions. From these investigations, we identify the experimental parameters that can yield comparable design efficiency across free recall data and traditional event-related designs. In Simulation 1, we investigate how efficiency changes as a function of tau, the parameter that determines the exponential part of the ex-Gaussian free recall latency distributions. In Simulation 2, we explore the joint effects of tau and number of free recall events on design efficiency. In addition, we present two fMRI experiments that empirically assess changes in detection power and estimation efficiency across different tau values. In Experiment 1, we used simulated free recall data sets derived from different tau values to generate the onsets and latencies of visual stimulation events. In Experiment 2, visual stimulation onsets and latencies were taken from empirical free recall data sets.
SIMULATIONS
Simulation 1
Because the exponential portion of the distribution (Equation 2) is thought to depend on the characteristics of the memory search engaged during free recall and determines the latencies of individual recall events (the Gaussian portion only impacts on the latency of the first recall item; see Rohrer & Wixted, 1994), our initial analyses focused on tau, the parameter that defines the exponential component of the latency distribution. Changes in tau can capture individual differences that might occur across participants’ free recall latencies. Furthermore, the lag (or jitter) across individual free recall events varies as a function of tau, which will also have an impact on design efficiency (Dale & Buckner, 1997). Accordingly, we evaluated how changes in this parameter affect design efficiency. We considered changes in tau across different models of free recall events (events or epochs) and different numbers of free recall conditions (1 vs. 2).
Methods
Free recall latencies were simulated using the ex-Gaussian distribution (Rohrer & Wixted, 1994). In order to investigate how changes in the exponential stage of the latency distributions affect fMRI design efficiency, a range of 30 tau values (1 to 30) was used to generate the recall latency distributions. The onsets of consecutive recall events were constrained to be a minimum of 250 msec apart. All additional free recall and fMRI parameters were held constant. Specifically, each simulated free recall run lasted 60 sec and consisted of 30 free recall events (i.e., the simulated number of recalled items). The sampling rate of fMRI, repetition time (TR), was 2 sec.
Separate data sets were simulated for one- and two-condition fMRI designs, and for each data set, design efficiency was assessed for cases when the data were modeled as events and as epochs. We should emphasize that our approach of using epochs between free recall events should not imply a theoretical standpoint with regard to free recall processes. We rather took this approach to be able to assess efficiency when there is little decay time between the individual events, and to evaluate whether there is enough variance in the latencies that would enable such events to be estimable. Accordingly, 1000 sets of simulations were conducted for each of the 30 tau values, totaling 30,000 simulations for the event and 30,000 simulations for the epoch models. For two-condition data sets, the order of event-related conditions was determined randomly.
Generation of the design matrices for each simulation was conducted under assumptions of the general linear model. For both the event and epoch models, the onset of individual free recall items was defined as the point in time when the preceding event was recalled. For epoch models, the duration of each individual epoch was defined as the time that passed between the recall of the preceding item and the current item. The resultant design matrix was convolved with a gamma function, which has been shown to provide a reasonable approximation of the HRF (Boynton, Engel, Glover, & Heeger, 1996). For simplicity, nuisance variables such as scanner drift were not entered into the design matrix.
Efficiency was calculated using Equation 1. For the one-condition data sets, the contrast matrix used was C = [1], in order to assess detection power for the comparison of the experimental condition to baseline. For the two-condition data sets, the contrast matrix was set to C = [1–1], in order to assess detection power for differences in neural activation across the two conditions. The resultant efficiency estimates were subjected to analyses of variance. All results reported below were statistically reliable at p < .01.
Results and Discussion
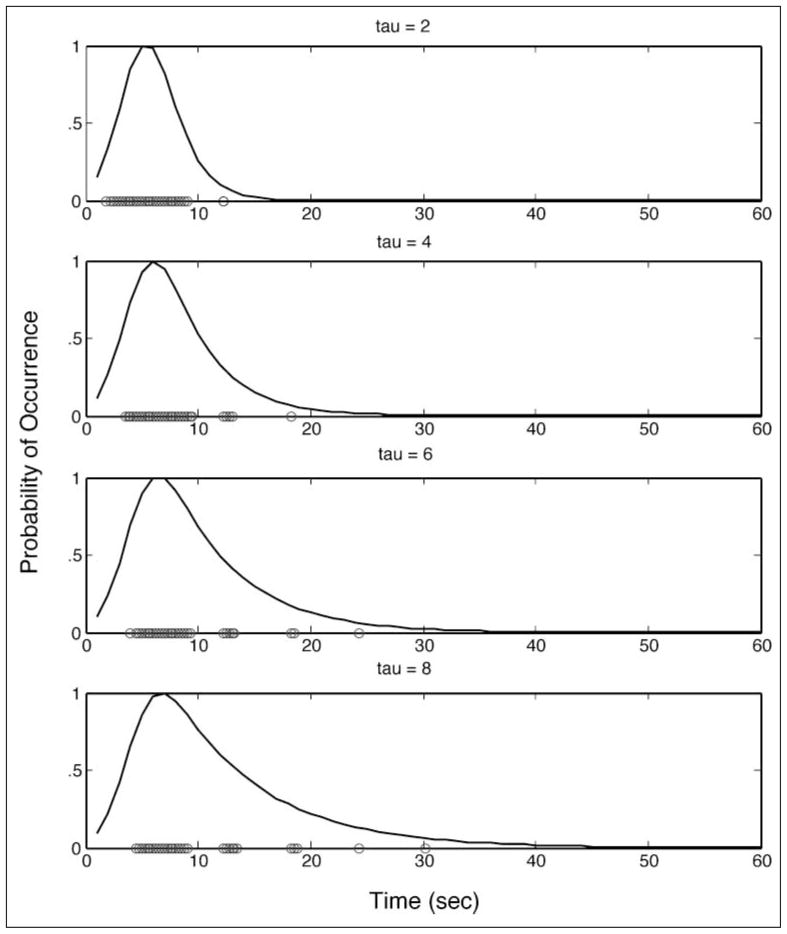
Figure 1 depicts the relationship between the shape of the free recall latency distribution and the values of tau. Note that as tau increases, the exponential decline in free recall rate is more prominent. The characteristics of the exponential portion—determined by tau—of the free recall distributions are important for design efficiency in that higher tau values yield greater variability in the time lags across individual free recall events, whereas lower tau values yield less variability in lags across the free recall onsets (i.e., individual onsets are more packed together in time) (illustrated in Figure 1).
Figure 1.
Free recall event probabilities across variations in the tau parameter as a function of time (sec). Circles indicate latencies of individual free recall events from Simulation 1. The early phase of each function has been enlarged in the inset.
One-condition fMRI data sets
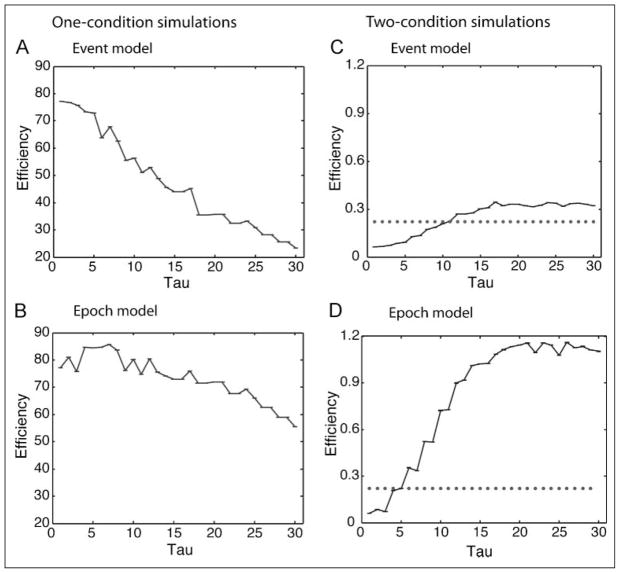
Figure 2A and B illustrate efficiency across the tau values for the one-condition simulated data set for event and epoch models, respectively. For both models (Figure 2A and B), efficiency decreases as tau increases. This decrease in efficiency likely occurs due to the fact that free recall onsets are closer together in time at smaller values of tau. As events cluster closer together, individual events become less distinguishable from one another, given the sampling rate (TR = 2), but the overall estimation of amplitude relative to baseline increases. In other words, as the events get closer together in time, they start to become equivalent to a block design, so detection power versus baseline improves.
Figure 2.
Efficiency across values of tau for the simulated data sets in Simulation 1: (A) the one-condition event model, (B) the one-condition epoch model, (C) the two-condition event model, (D) the two-condition epoch model. The horizontal reference line on C and D indicates the efficiency for the two-condition jittered event-related design. Error bars plot standard error of the mean across 1000 simulations. Note that one-condition designs have greater efficiency compared to two-condition designs, which results in the discrepancy across the scales.
Two-condition fMRI data sets
Two-condition data sets can require distinguishing successive events that may come from different conditions and so presents the primary challenge for studying free recall with fMRI. Figure 2C and D indicate efficiency across tau for the two-condition simulated data set for event and epoch models, respectively. The figures indicate that for both the event and epoch models, larger tau yields greater design efficiency when differential neural activation needs to be assessed between the two conditions (i.e., Condition A > Condition B). With larger tau values, individual free recall events are more scattered (i.e., jittered) (see Figure 1), thus efficiency in assessing the difference in neural activation across the two conditions increases. Notably, the figures also indicate that the beneficial effect of tau on efficiency plateaus around tau of 17, where efficiency no longer increases. However, note that our simulations were limited to a free recall period of 60 sec. For longer free recall periods, increasing tau may keep increasing efficiency for even larger tau values.
To summarize, efficiency is generally higher for larger tau values for both the event and epoch models. We should also note that the epoch model has higher overall design efficiency compared to the event model. In addition, design efficiency is higher for the one-condition compared to the two-condition designs for both event and epoch models.
Traditional Event-related Design Simulations
As a comparison to the simulated free recall data sets, we simulated traditional two-condition event-related designs. To be consistent with the reported simulations, the first simulation generated a scan period of 60 sec. This design contained 10 trials from each experimental condition, with 10 jittered null intervals ranging from 2 to 8 sec (totaling 40 sec), which ensured that the design approximated traditional event-related fMRI designs with jittered null intervals between experimental trials. To match the number of trials with the reported simulations, we simulated a second design containing 15 trials from each experimental condition, with 15 jittered null intervals ranging from 2 to 8 sec (totaling 60 sec), totaling a scan duration of 100 sec. The inclusion of jittered null intervals in the traditional event-related design increased the total duration of the scan time when the number of trials was matched to those in simulations, as there were no null trials in the simulated data sets. The order of experimental conditions and the null intervals in both simulations was randomized. Consistent with Simulation 1, TR was set to 2 sec. Efficiency was calculated using Equation 1. The event-related design with matched scan time to the free recall design yielded an efficiency of 0.20, which approximates efficiency of a simulated free recall data set with tau of 8 (Figure 2C). The second design matched the number of trials to Simulation 1 across 1000 simulations. This jittered event-related design had an efficiency value of 0.22, close to the free recall data set with tau 10 for the event model. Moreover, for both simulations, the larger tau values have even greater efficiency than these traditional event-related designs. These results indicate that free recall designs that have latency distributions with large tau values (specifically 10 or larger) can yield comparable efficiency to traditional event-related designs with equated numbers of trials or scan length.
Simulation 2
Next, we evaluated how the number of successfully retrieved items, or recall accuracy, would affect design efficiency. Specifically, we assessed how the number of free recall events affects design efficiency jointly with differences in the tau parameter.
Methods
Simulated fMRI data sets varied tau over the same range of values used in Simulation 1. The number of free recall events was manipulated over a range of 5 to 30 items recalled. The TR was set to 2 sec. Simulation and design efficiency estimation methods were otherwise identical to Simulation 1.
Results and Discussion
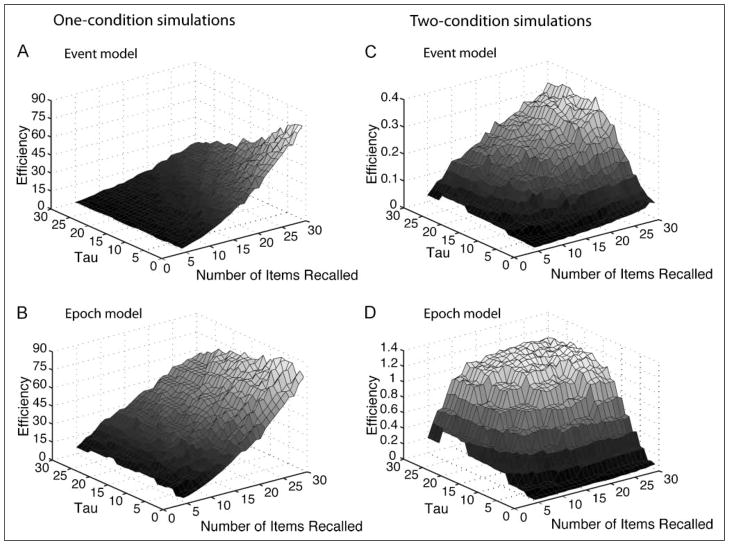
Figure 3A and B illustrate efficiency across values of tau and the number of free recall items for the one-condition fMRI design modeled as events and epochs respectively. Likewise, Figure 3C and D show efficiency across conditions and models for the two-condition fMRI design. Overall, a larger tau and more items recalled yield best efficiency. This effect is more prominent for the two-condition fMRI designs, for both the event and epoch models. Also, note that in line with Simulation 1, design efficiency is higher for the one-condition compared to the two-condition designs, and the epoch models yield overall higher efficiency than event models.
Figure 3.
Efficiency across values of tau and total number of free recall events for the simulated data sets in Simulation 2 (A) for the one-condition event model, (B) for the one-condition epoch model, (C) for the two-condition event model, and (D) for the two-condition epoch model.
EXPERIMENTS
The simulations indicate that free recall data can yield feasible fMRI design efficiency under certain conditions. Specifically, simulated free recall latency distributions with larger tau values and higher free recall accuracy produce better design efficiency.
To further establish the feasibility of distinguishing BOLD activation between two free recall conditions, we conducted simple visual stimulation experiments in which the onsets of left versus right hemifield visual stimulation correspond to different conditions from free recall latency distributions. Following others (e.g., Dale & Buckner, 1997; Boynton et al., 1996), the logic of this approach is that the response to visual stimulation within primary visual cortex (V1) is well known and highly robust (e.g., Ress & Heeger, 2003; Heeger, 1999). That is, to the extent that the basic assumptions about the hemodynamic response are the same between visual stimulation and free recall, we can use visual stimulation to evaluate efficiency of free recall events that have the same temporal characteristics. Thus, to the degree that left versus right hemifield stimulation at free recall latencies can distinguish right versus left hemisphere activation in V1, this can be interpreted as the upper limit of detection power for an fMRI experiment that tests true free recall conditions. In Experiment 1, free recall latencies were generated with the routine described in Simulation 1, for three different tau values. In Experiment 2, we conducted the same experiment, using empirical free recall latency distributions to determine the onset of visual stimulation.
Experiment 1
The goal of Experiment 1 was to demonstrate the feasibility of distinguishing individual free recall events across values of tau, consistent with our simulations. In order to complement the results from the simulations reported above, we derived latency distributions for two-condition free recall data sets with a range of tau values (2, 5, and 8) using the ex-Gaussian distribution and simulation methods described above. It should be noted that these values of tau were smaller than those yielding comparable efficiency to traditional event-related designs (see Figure 2C). The onsets of these two conditions were then used as the onsets for visual stimulation of the right or left hemifield. This approach allowed us to empirically assess the ability to detect a reliable difference between conditions in visual cortex activation across the three tau values.
Methods
Participants
Two right-handed adults (2 women, ages 21 and 28 years) participated in the experiment. Informed consent was obtained in accordance with the Human Research Protections Office at Brown University. Participants had normal or corrected-to-normal vision.
Design and procedure
Participants were instructed to fixate on a cross presented on the center of the screen. On each trial, a checkerboard pattern was presented for 150 msec to either the left or right visual field. The timing of individual checkerboard onsets across trials was derived from free recall latency simulations of two recall conditions, employing a tau of either 2, 5, or 8 as described in Simulation 1. For each tau variation, participants completed two blocks in each of two separate runs with the two free recall conditions assigned to left versus right checkerboard stimulation consistent within a run. The left–right assignment was counterbalanced across the two runs. This design structure resulted in two runs that each contained six blocks of 30 trials.
fMRI protocol
Whole-brain imaging was performed on a Siemens 3-T TIM Trio MRI system. Functional images were acquired using a gradient-echo echo-planar sequence (TR = 2 sec, TE = 30 msec, flip angle = 90°, 33 axial slices, 3.5 × 3.5 × 3.5 mm). Following the functional runs, high-resolution T1-weighted (MP-RAGE) anatomical images were collected for visualization. Head motion was restricted using firm padding that surrounded the head. Visual stimuli were projected onto a screen, and viewed through a mirror attached to a standard head coil.
Image processing
Image processing and data analysis were performed using SPM2 (www.fil.ion.ucl.ac.uk/spm/). Following quality assurance procedures to assess outliers or artifacts in volume and slice-to-slice variance in the global signal, functional images were corrected for differences in slice acquisition timing by resampling all slices in time to match the first slice, followed by motion correction across all runs (using sinc interpolation). Functional data were then normalized based on MNI stereotaxic space using a 12-parameter affine transformation along with a nonlinear transformation using cosine basis functions. Images were resampled into 3-mm3 voxels and then spatially smoothed with an 8-mm FWHM isotropic Gaussian kernel.
fMRI data analysis
Data analysis was conducted under the assumptions of the general linear model as implemented in SPM2. Separate regressors were generated for each condition arising from a combination of hemifield and tau value (left or right checkerboard presentation for each of the three tau variations) and were modeled using a canonical HRF and its temporal derivative to partially account for systematic error due to deviations of the HRF from the canonical form. Data across the two runs were modeled as separate sessions. For each subject, statistical effects were estimated using a subject-specific fixed effects model, with session-specific effects and low-frequency signal components (<0.01 Hz) treated as confounds. Regions that exceeded an FDR corrected threshold of p < .05 were considered reliable.
Whole-brain statistical analyses were complemented by region-of-interest (ROI) analyses. Percent BOLD signal change in ROIs emerging from functional contrasts was derived using the MarsBaR ROI toolbox for SPM (http://marsbar.sourceforge.net/). To evaluate estimation efficiency, the estimated responses were then fit with a gamma function, which has been previously shown to provide a good approximation of the HRF (e.g., Boynton et al., 1996).
Results and Discussion
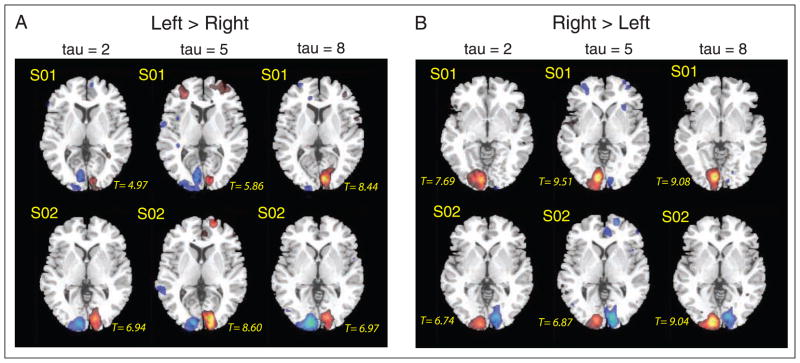
The contrast of left versus right visual field stimulation resulted in activation in right visual cortex for all three tau variations (see Figure 4, left). The reverse contrast indicated greater activation in left visual cortex. This was true for both participants, across all three tau values (Figure 4, right). Thus, in general, it is feasible to distinguish neural activation across separate conditions that onset according to free recall latency distributions even with small tau values.
Figure 4.
Results from voxelwise contrasts across participants in Experiment 1. Regions that show enhanced activation for the left compared to the right visual field presentation (left), and regions that exhibit greater activation for the right compared to the left visual field presentation (right).
Next, we assessed the relationship between tau and detection power. Specifically, as depicted in Figure 4, activation in visual cortex was greater for tau values 5 and 8 compared to tau 2 (see Figure 4 for t statistics associated with each tau across the two participants). Hence, consistent with the simulations, the reported data suggest that free recall latency distributions with larger tau values would yield greater detection power.
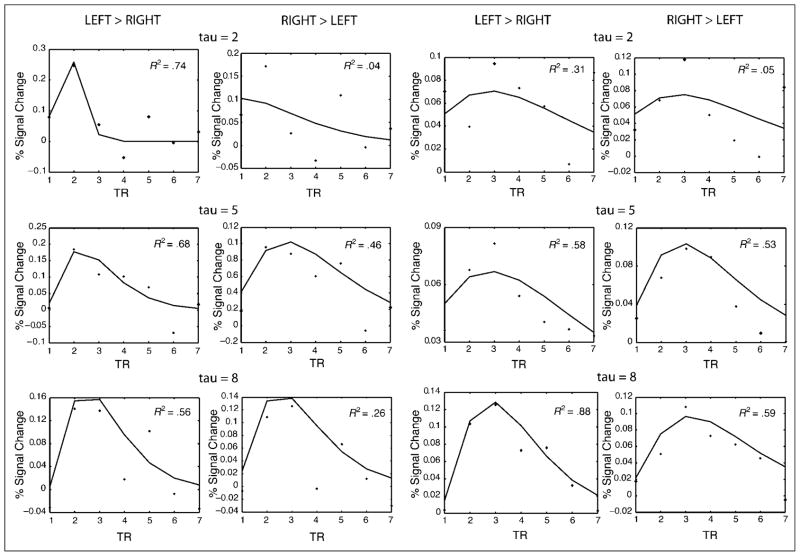
It is also important to determine to what extent it is possible to estimate the shape of the HRF without making an assumption about its shape (i.e., estimation efficiency). Thus, we evaluated our ability to estimate peristimulus changes in percent signal change across values of tau. To do so, we conducted ROI analyses centered on the regions depicted in Figure 4. Figure 5 plots the estimated percent signal change, poststimulus onset, and the corresponding gamma function fits. Overall, goodness of fit for tau 2 is worse than tau 5–8, suggesting that very small tau values may yield worse estimation efficiency.
Figure 5.
ROI analyses for the active regions reported in Figure 4 across the three tau values (Participant 01 presented on the left, Participant 02 presented on the right). Symbols indicate percent BOLD signal change. Smooth lines indicate the gamma function fit to the percent BOLD signal change in each region.
Overall, results from this experiment converge with the findings from the simulations reported above in showing that free recall data sets with larger tau values will have higher detection power. Furthermore, free recall latency distributions with larger tau values may permit better estimation of the hemodynamic response, and so yield better estimation efficiency.
Experiment 2
In the next experiment, our goal was to generalize the results from Experiment 1, providing a model-free test of whether differential neural activation for two free recall conditions can be distinguished, using empirically derived free recall data rather than simulated data sets. We first conducted a behavioral experiment (Experiment 2A) during which participants studied a list of words, and following a 1-min distractor period, were asked to recall the study list in any order they chose. The study words consisted of two conditions (semantically related and unrelated words), allowing us to obtain free recall latency distributions for the two conditions. Then, we used the onsets of recalled related and unrelated words obtained in Experiment 2A to determine the onsets of visual hemifield stimulation during an fMRI experiment (Experiment 2B). This approach allowed us to determine the differential neural activation associated with onsets of two free recall conditions, using the latencies obtained from an actual free recall behavioral experiment.
Experiment 2A
Methods
Participants
Four adults (4 women, ages 18–28 years) participated in the experiment. Informed consent was obtained in accordance with the Human Research Protections Office at Brown University. Participants were paid for their participation.
Design and procedure
The experiment consisted of five blocks. In each block, participants studied a list of 30 words (presented on the center of the screen for 2000 msec each), half of which were drawn from the same category (e.g., banana, apple), and half of which were unrelated words (e.g., stadium, staircase). Category membership was determined based on normative data (Battig & Montague, 1969). A distractor period followed the study phase, during which participants solved math problems for 1 min. Following the distractor phase, participants were asked to recall the words they had studied during the encoding period. Participants had 1 min to recall as many words as they could. The latency and condition (category, noncategory) of each recalled word was recorded.
Results and discussion
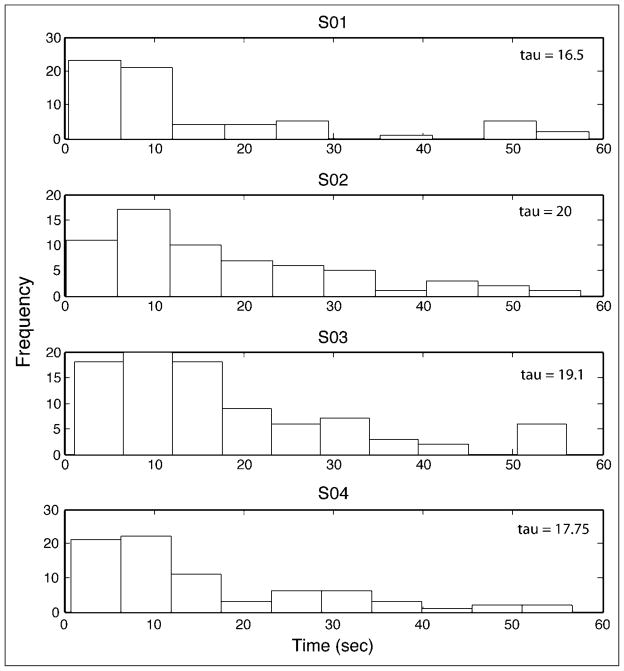
Figure 6 illustrates the free recall latency distributions across the four participants. The tau values associated with each distribution were 16.5, 20, 19.1, and 17.75, respectively. These latency distributions are consistent with previous reports of free recall latency distributions (e.g., Rohrer & Wixted, 1994). However, note that these tau values are notably larger than those evaluated in Experiment 1, hence, the results from Experiment 1 should be considered conservative estimates of efficiency during free recall.
Figure 6.
Free recall latency distributions and corresponding tau values across the four participants in Experiment 2A.
Experiment 2B
Methods
Subjects
Three right-handed (3 women, ages 18–23 years) participated in the experiment. Informed consent was obtained in accordance with the Human Research Protections Office at Brown University. Participants had normal or corrected-to-normal vision, and were paid for their time.
Design and procedure
Design and procedure were identical to Experiment 1, with the exception that the timing of the checkerboard onsets was derived from the empirical latency distributions obtained from Experiment 2A. Incorrectly recalled words (consisting of approximately 3% of the total number of recalled words) were included in the model and analyses. These trials were not excluded, as the primary goal was to identify whether distinguishing neural activation across conditions that onset according to actual free recall latencies would be possible. The tau values for the latency distributions corresponding to each participant were 16.5, 17.75, and 20, respectively. The onsets of each checkerboard presentation were yoked to one of the four participants’ latency distributions in Experiment 2A, with left and right visual presentation corresponding to the two conditions (category and noncategory words). The assignment of the two conditions to left and right visual presentation was counterbalanced across two runs.
fMRI procedures and data analysis
fMRI protocol, image processing, and data analysis procedures were identical to Experiment 1.
Results and discussion
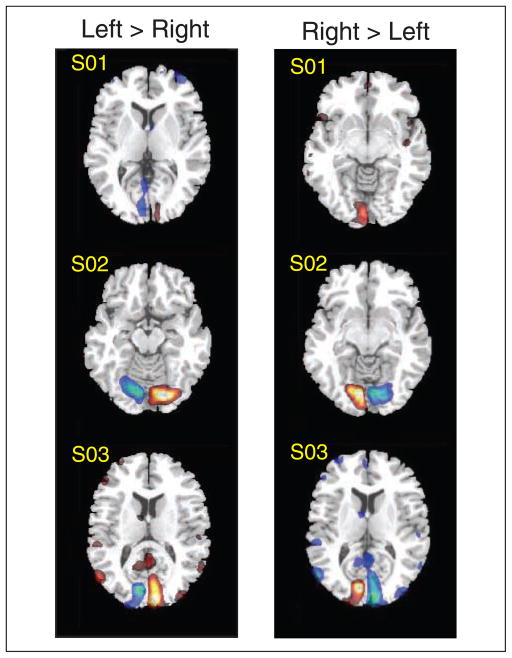
As in Experiment 1, regions that exhibit more neural activation to the presentation of the checkerboard stimuli on the left visual field were identified by subtracting trials that contained the checkerboard presentation on the right visual field from trials that contained the presentation on the left visual field. For all participants, these analyses revealed increased activation in right visual cortex (see Figure 7, left). The reverse analyses indicated increased activation in left visual cortex for all participants (Figure 7, right). Hence, the data replicate Experiment 1 in suggesting that distinguishing neural activation across two types of free recall events is possible, also using empirically derived free recall latency distributions.
Figure 7.
Results from voxelwise contrasts across participants in Experiment 2B. Regions that show enhanced activation for the left compared to the right visual field presentation (left), and regions that exhibit greater activation for the right compared to the left visual field presentation (right).
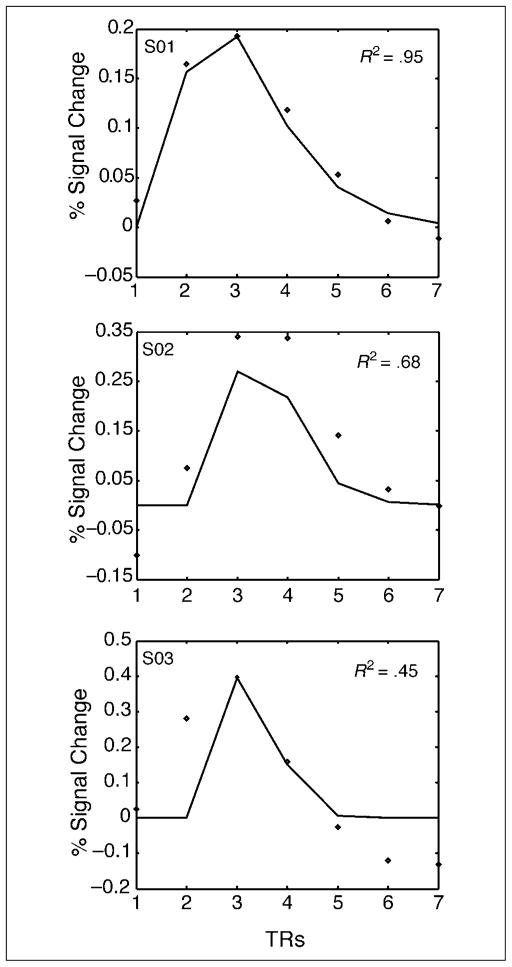
In addition, we also evaluated estimation efficiency, the ability to estimate the shape of the HRF. To do so, as in Experiment 1, we conducted ROI analyses centered on the regions illustrated in Figure 7 for the three participants. Figure 8 plots the estimated percent signal change, poststimulus onset, and the corresponding gamma function fits across our participants for the regions presented on the right panel of Figure 7. As illustrated in Figure 8, goodness of fit across the three participants ranged from .45 to .95.
Figure 8.
ROI analyses for the active regions reported in Figure 7 across participants. Symbols indicate percent BOLD signal change. Smooth lines indicate the gamma function fit to the percent BOLD signal change in each region.
DISCUSSION
In this research, we aimed to assess the feasibility of distinguishing free recall events using fMRI. Our approach was to evaluate how changes in conditions and variables that describe free recall latency distributions and fMRI designs will affect design efficiency. Specifically, we investigated how differences in the shape of the exponential part of the free recall latency distribution (determined by the parameter tau), the total number of free recall events, the type of model (event vs. epoch), and the number of free recall conditions in the design (1 vs. 2) affected fMRI design efficiency. Overall, results from the simulations suggest that free recall data can yield comparable design efficiency to traditional event-related designs, and data from two fMRI experiments confirm that neural activation can be distinguished across two free recall conditions. Below we summarize our findings and discuss their implications.
The tau parameter of free recall latency distributions determines the time lags among individual free recall events, and consequently, constitutes an important determinant of design efficiency in free recall. Our simulation results indicated that when neural activation for two conditions needs to be distinguished, larger tau values yield greater design efficiency. Data from visual stimulation experiments that varied tau to generate onsets of two visual stimuli (presented either on the left or right visual field) yielded greater activation in contralateral visual cortex, suggesting that distinguishing neural activation for free recall events is possible even at small values of tau. However, the magnitude of neural activation in the identified visual cortex regions was greater for larger tau values, indicating higher detection power. In addition, larger tau values yielded better characterization of the HRF, leading to better estimation efficiency. Accordingly, tau might be an important determinant of optimal design efficiency when researchers are focused on regions that have overall lower signal intensity (such as the medial temporal lobes), and in cases when the HRF needs to be estimated. Under such circumstances, it might be beneficial to prescreen participants and determine the tau values from their behavioral free recall latency distributions, and exclude those with a low tau. Although such prescreening could threaten the representativeness of sample, previous research on free recall latency distributions suggests that very small tau values are unlikely (e.g., see Rohrer & Wixted, 1994).
With respect to modeling individual free recall items, our approach was to compare modeling individual free recall items as events versus epochs in order to assess efficiency for cases when there is minimal decay period between individual events. Importantly, our simulations demonstrate that efficiency is not worse as a consequence of such an epoched response, but rather improves detection power. However, from a theoretical perspective, we should stress that researchers may wish to model individual free recall items differently than the approach taken in our study. For instance, several models (e.g., Polyn, Norman, & Kahana, 2009; Becker & Lim, 2003; Howard & Kahana, 2002; Anderson & Bower, 1972, 1974; Kintsch, 1970, 1974) suggest that free recall may entail multiple processes that are temporally aligned with or may occur at different frequencies than actual recall responses. Thus, researchers may also model multiple processes that contribute to free recall. To the extent that such processes exist, they should be estimable in the way they are in any other fMRI study of complex cognition, as the feasibility of modeling multiple temporally uncorrelated temporal processes that occur at different lags during a single task with fMRI has already been established (e.g., Visscher et al., 2003; Donaldson, Petersen, Ollinger, & Buckner, 2001). We believe that the availability of extensive behavioral and modeling work conducted with free recall will enable researchers to employ a range of modeling options and apply the appropriate process model for their particular data set.
Finally, different participants will have variable success at free recall, and thus, one also lacks control over the number of free recall events. Our simulations indicated that efficiency increased as a function of the number of free recall events. This is primarily due to the fact that greater number of events will increase degrees of freedom, which would increase the power of a statistical inference. Furthermore, in the case of free recall, greater number of free recall events will also introduce more individual events that occur more scattered in time due to the nature of the free recall latency distributions. This latter fact was evident from the finding of an interaction between latency and free recall success such that the highest efficiency was obtained for the larger tau values and highest number of free recall events.
Before concluding, we should also note that conditional entropy may be another factor that could affect design efficiency in free recall. In addition to lack of control over the latencies and number of individual free recall events, researchers also do not have control over the order of free recall events from different conditions. In the simulations reported in the current investigation, the order of free recall items belonging to two different conditions was generated randomly, assuming high conditional entropy. However, this may not be the case in every research design, and may differ depending on the experimental manipulation of interest. Nonetheless, Experiment 2, which used an actual free recall data set to generate onsets of two visual stimuli and so did not have ideal conditional entropy, indicated that distinguishing neural activation across actual two free recall conditions was still possible. In addition, we should note that our results suggest that much of the efficiency in an ex-Gaussian distribution of free recall latency is captured by the long tail of the distribution. Thus, were experimental conditions to differ significantly in their occurrence between the beginning and end of the retrieval period, these conditions could have different efficiency.
In conclusion, we have shown that the natural latency distribution of free recall makes analysis of the BOLD signal associated with free recall events feasible. Thus, we hope that the results of these simulations and the reported data can provide a guideline for memory researchers to implement designs for studying free recall with fMRI.
Acknowledgments
External support came from the National Science Foundation (award 0521432) related to the purchase of the MRI system.
References
- Anderson JR, Bower GH. Recognition and retrieval processes in free recall. Psychological Review. 1972;79:97–123. [Google Scholar]
- Anderson JR, Bower GH. A propositional theory of recognition memory. Memory & Cognition. 1974;2:406–412. doi: 10.3758/BF03196896. [DOI] [PubMed] [Google Scholar]
- Andreasen NC, O’Leary DS, Arndt S, Cizadlo T, Rezai K, Watkins GL, et al. I. PET studies of memory: Novel and practiced free recall of complex narratives. Neuroimage. 1995a;2:284–295. doi: 10.1006/nimg.1995.1036. [DOI] [PubMed] [Google Scholar]
- Andreasen NC, O’Leary DS, Arndt S, Cizadlo T, Rezai K, Watkins GL, et al. II. PET studies of memory: Novel and practiced free recall of word lists. Neuroimage. 1995b;2:296–305. doi: 10.1006/nimg.1995.1037. [DOI] [PubMed] [Google Scholar]
- Barch DM, Sabb FW, Carter CS, Braver TS, Noll DC, Cohen JD. Overt verbal responding during fMRI scanning: Empirical investigations of problems and potential solutions. Neuroimage. 1999;10:642–657. doi: 10.1006/nimg.1999.0500. [DOI] [PubMed] [Google Scholar]
- Battig WF, Montague WE. Category norms for verbal items in 56 categories: A replication and extension of the Connecticut category norms. Journal of Experimental Psychology Monograph. 1969;80:1–46. [Google Scholar]
- Becker S, Lim J. A computational model of prefrontal control in free recall: Strategic memory use in the California verbal learning task. Journal of Cognitive Neuroscience. 2003;15:821–832. doi: 10.1162/089892903322370744. [DOI] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. Journal of Neuroscience. 1996;16:4207–4221. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burbeck SL, Luce RD. Evidence from auditory simple reaction times for both change and level detectors. Perception & Psychophysics. 1982;32:117–133. doi: 10.3758/bf03204271. [DOI] [PubMed] [Google Scholar]
- Cusack R, Cumming N, Bor D, Norris D, Lyzenga J. Automated post-hoc noise cancellation tool for audio recordings acquired in an MRI scanner. Human Brain Mapping. 2005;24:299–304. doi: 10.1002/hbm.20085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM. Optimal experimental design for event-related fMRI. Human Brain Mapping. 1999;8:109–114. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<109::AID-HBM7>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Buckner R. Selective averaging of rapidly presented individual trials using fMRI. Human Brain Mapping. 1997;5:329–340. doi: 10.1002/(SICI)1097-0193(1997)5:5<329::AID-HBM1>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Dickerson BC, Miller SL, Greve DN, Dale AM, Albert MS, Schacter DL, et al. Prefrontal–hippocampal–fusiform activity during encoding predicts intraindividual differences in free recall ability: An event-related functional–anatomic MRI study. Hippocampus. 2007;17:1060–1070. doi: 10.1002/hipo.20338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donaldson DI, Buckner RL. Effective paradigm design. In: Matthews PM, Jezzard P, Evans AC, editors. Functional magnetic resonance imaging of the brain: Methods for neuroscience. Oxford: Oxford University Press; 2000. [Google Scholar]
- Donaldson DI, Petersen SE, Ollinger JM, Buckner RL. Dissociating state and item components of recognition memory using fMRI. Neuroimage. 2001;13:129–142. doi: 10.1006/nimg.2000.0664. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Zarahn E, Josephs O, Henson RNA, Dale AM. Stochastic designs in event-related fMRI. Neuroimage. 1999;10:607–619. doi: 10.1006/nimg.1999.0498. [DOI] [PubMed] [Google Scholar]
- Gillund G, Shiffrin RM. A retrieval model for both recognition and recall. Psychological Review. 1984;91:1–67. [PubMed] [Google Scholar]
- Heeger DJ. Linking visual perception with human brain activity. Current Opinion in Neurobiology. 1999;9:474–479. doi: 10.1016/S0959-4388(99)80071-3. [DOI] [PubMed] [Google Scholar]
- Henson RN. Analysis of time series: Linear time-invariant models, event-related fMRI and optimal experimental design. In: Frackowiak R, Friston K, Frith C, Dolan B, Price C, editors. Human brain function. 2. London: Elsevier; 2004. pp. 793–822. [Google Scholar]
- Howard MW, Kahana MJ. A distributed representation of temporal context. Journal of Mathematical Psychology. 2002;46:269–299. [Google Scholar]
- Kintsch W. Models for free recall and recognition. In: Norman DA, editor. Models of human memory. New York: Academic Press; 1970. [Google Scholar]
- Kintsch W. The representation of meaning in memory. Hillsdale, NJ: Erlbaum; 1974. [Google Scholar]
- Liu TT. Efficiency, power, and entropy in event-related fMRI with multiple trial types: Part II. Design of experiments. Neuroimage. 2004;21:400–413. doi: 10.1016/j.neuroimage.2003.09.031. [DOI] [PubMed] [Google Scholar]
- Liu TT, Frank LR. Efficiency, power and entropy in event-related FMRI with multiple trial types: Part 1. Theory. Neuroimage. 2004;21:387–400. doi: 10.1016/j.neuroimage.2003.09.030. [DOI] [PubMed] [Google Scholar]
- Liu TT, Frank LR, Wong EC, Buxton RB. Detection power, estimation efficiency, and predictability in event-related fMRI. Neuroimage. 2001;13:759–773. doi: 10.1006/nimg.2000.0728. [DOI] [PubMed] [Google Scholar]
- Ollinger JM, Corbetta M, Shulman GL. Separating processes within a trial in event-related functional MRI: II. The analysis. Neuroimage. 2001;13:218–229. doi: 10.1006/nimg.2000.0711. [DOI] [PubMed] [Google Scholar]
- Ollinger JM, Shulman GL, Corbetta M. Separating processes within a trial in event-related functional MRI: I. The method. Neuroimage. 2001;13:210–217. doi: 10.1006/nimg.2000.0710. [DOI] [PubMed] [Google Scholar]
- Petersson KM, Sanblom J, Gisselgard J, Ingvar M. Learning-related modulation of functional retrieval networks in man. Scandinavian Journal of Psychology. 2001;42:197–216. doi: 10.1111/1467-9450.00231. [DOI] [PubMed] [Google Scholar]
- Polyn SM, Natu VS, Cohen JD, Norman KA. Category-specific cortical activity precedes retrieval during memory search. Science. 2005;310:1963–1966. doi: 10.1126/science.1117645. [DOI] [PubMed] [Google Scholar]
- Polyn SM, Norman KA, Kahana MJ. A context maintenance and retrieval model of organizational processes in free recall. Psychological Review. 2009;116:129–156. doi: 10.1037/a0014420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raaijmakers JGW, Shiffrin RM. Search of associative memory. Psychological Review. 1981;88:93–134. [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychological Review. 1979;85:59–108. [Google Scholar]
- Ress D, Heeger DJ. Neuronal correlates of perception in early visual cortex. Nature Neuroscience. 2003;6:414–420. doi: 10.1038/nn1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricker JH, Muller RA, Zafonte RD, Black KM, Millis SR, Chugani H. Verbal recall and recognition following traumatic brain injury: A [O-15]-water positron emission tomography study. Journal of Clinical Experimental Neuropsychology. 2001;23:196–206. doi: 10.1076/jcen.23.2.196.1204. [DOI] [PubMed] [Google Scholar]
- Rohrer D, Wixted JT. An analysis of latency and interresponse time in free recall. Memory & Cognition. 1994;22:511–524. doi: 10.3758/bf03198390. [DOI] [PubMed] [Google Scholar]
- Staresina BP, Davachi L. Differential encoding mechanisms for subsequent associative recognition and free recall. Journal of Neuroscience. 2006;6:9162–9172. doi: 10.1523/JNEUROSCI.2877-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher KM, Miezin FM, Kelly JE, Buckner RL, Donaldson DI, McAvoy MP, et al. Mixed blocked/event designs separate transient and sustained activity in fMRI. Neuroimage. 2003;19:1694–1708. doi: 10.1016/s1053-8119(03)00178-2. [DOI] [PubMed] [Google Scholar]
- Wager TD, Nichols TE. Optimization of experimental design in fMRI: A general framework using a genetic algorithm. Neuroimage. 2003;18:293–309. doi: 10.1016/s1053-8119(02)00046-0. [DOI] [PubMed] [Google Scholar]
- Wixted JT, Rohrer D. Proactive interference and the dynamics of retrieval. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1993;19:1024–1039. [Google Scholar]
- Wixted JT, Rohrer D. Analyzing the dynamics of free recall: An integrative review of the empirical literature. Psychonomic Bulletin & Review. 1994;1:89–106. doi: 10.3758/BF03200763. [DOI] [PubMed] [Google Scholar]