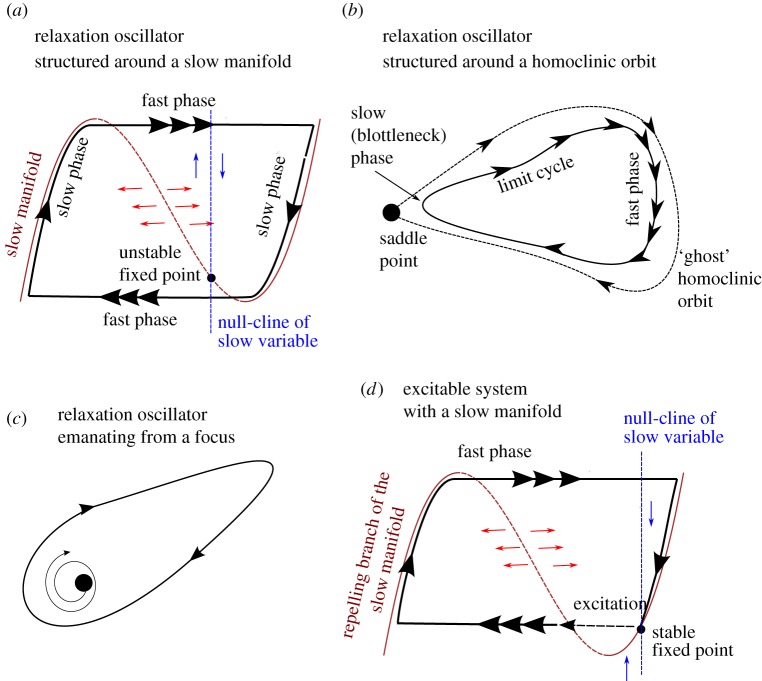
Figure 2.

Schematic of several forms of relaxation oscillations. (a) The vector space is structured by a slow manifold with several stable branches. All points of the state space are attracted towards the stable branches of the slow manifold (solid lines) along the fast direction, which is here the horizontal. The slow evolution consists of an upward or downward course along the slow manifold depending on whether the system lives on the right- or left-hand side of the null-cline of the slow variable. The relaxation oscillation consists of alternate jumps between the two branches of the slow manifold. (b) Trajectories are rapidly attracted towards a region of the phase space influenced by a saddle point. In the scenario displayed here, there exists a combination of parameters for which the limit cycle crosses the saddle point. In that case, the period of the orbit, which includes the saddle–node, is infinitely long. It is a ‘homoclinic orbit’, hence this particular bifurcation is named a homoclinic bifurcation. The homoclinic orbit only exists at the bifurcation point, but it influences the orbit when the parameter is close to the bifurcation. This is the reason why one refers to the ‘ghost’ of the homoclinic orbit. There is another scenario for which different saddle–nodes are connected to each other. The orbit and the associated bifurcation are then said to be ‘heteroclinic’. (c) The relaxation oscillation is organized around a fixed point, with complex eigenvalues with a positive real part. The bifurcation giving rise to this orbit is a Hopf bifurcation. (d) One example of excitability, here depicted for a slow–fast system. The system resides in a stable space, but a fluctuation may cause an ejection out of the unstable (dashed lines) branch of the slow manifold. The system then loops all the way through the slow manifold before coming back to rest. (Online version in colour.)