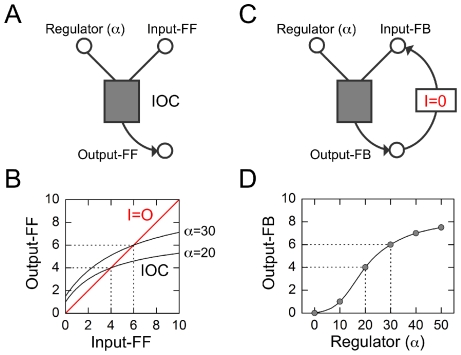
Figure 2. Predicting feedback responses.

(A) Consider a black box that transforms a regulatable input into a measurable output, where properties of this transformation might depend on some external regulator. (B) For a fixed regulator value α, we map out the input-output characteristic (IOC) by varying the input and measuring the resulting output (black curve). (C) If the output is now fed back into the input, the two values are forced to match. This condition only obtains at special points where the IOC intersects the line of equivalence I = 0 (red line, Fig. 2B). These intersection points determine all possible steady-state responses of the feedback system, though this graphical argument is agnostic regarding the stability of steady-states. (D) If the regulator level α is now changed, the IOC must again be measured, and the new feedback response predicted. By iterating this process, we obtain the full feedback response as a function of α.