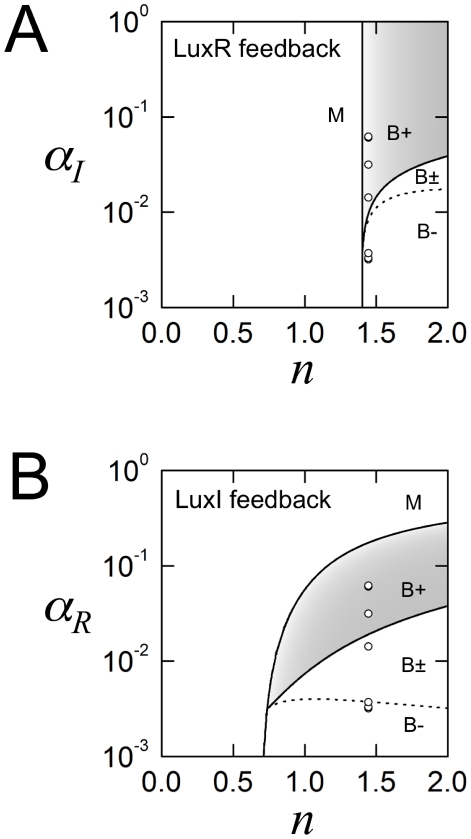
Figure 6. The interplay of regulation, promoter logic, and feedback.

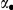(A) Response types for the LuxR-feedback topology, with LuxI as the regulator. (B) Response types for the LuxI-feedback topology, with LuxR as the regulator. Each panel shows an identical slice of parameter space: the Hill coefficient of LuxR-DNA binding is varied along the x-axis; the transcription rate of the regulator is varied along the y-axis; all other parameters are fixed at their autonomous loop values given in Table S3. The parameters corresponding to our autonomous loop experiments are shown as seven partly overlapping white dots, whose positions are identical in the two panels: their x-coordinates are given by the fitted Hill coefficient  = 1.45; their y-coordinates are given by the seven IPTG-induced pLac transcription rates, obtained using Eq. S4 with parameters from Table S4. The boundaries between the four DDR types are computed numerically; any differences in these DDR boundaries between the two panels can be attributed to topology alone. Both LuxR-feedback and LuxI-feedback topologies can generate all four types of density-dependent responses; however, given the same microscopic parameters the two topologies can show distinct behaviors. The observed LuxR-feedback responses happens to fall near the monostable type M boundary, while the observed LuxI-feedback responses are solidly within the bistable type B region. Generically, for a given ‘hard-wired’ value of the LuxR-feedback response will be either type M (smooth) or type B (abrupt). In contrast, as long as is sufficiently high, the LuxI-feedback system can be tuned between smooth and abrupt responses by varying the regulator level 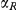. Moreover, the LuxI-feedback system can achieve abrupt responses over a broader range of values. These figures are qualitatively unchanged for other values of the fixed parameters (Supporting Information, Text S1: Bifurcation analysis of feedback loops).