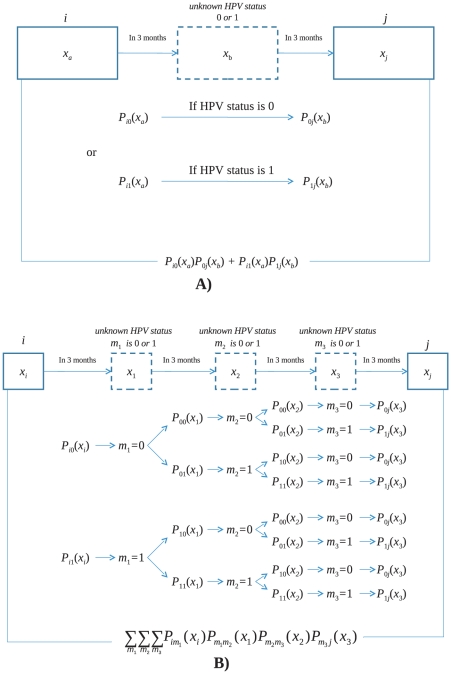
Figure 1. Reconstruction of information about the missed measurements when one HPV status is unknown ( Figure 1A ) or several (e.g., three) HPV statuses in a raw are missed ( Figure 1B ).

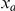Here, denotes the set of predictors of HPV clearance probability, such as CD4 count, HIV-1 VL, HAART, and HPV type. When one HPV measurement is unknown (Figure 1A), i and j describe the HPV status at the first and third visits, respectively, and parameters and 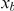denote the sets of predictors for transitions between first-to-second and second-to-third visits, respectively. The probability of changing HPV status from the first (i.e., known) state of HPV infection i to the status of HPV infection at the second visit (i.e., unknown) is P_{i 0}(x_a) when HPV status at the second visit is negative (i.e., “0”) or P_{i 1}(x_a) when it is positive (i.e., “1”). Respectively, at the third visit (with measured/known HPV status) HPV status j can be defined as P _0j(x_b) when at the second visit it supposed to be HPV-negative, and P _1j(x_b) when at the second visit it supposed to be HPV-positive. The sum over two possible intermediate states contributes to the total transition probability: so, the transition probability between two subsequent visits with measured HPV status could be presented as 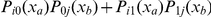. When three subsequent HPV status are unknown (Figure 1B), there are eight different combinations of HPV statuses in these states, each denoted by 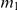, , 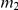and 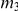as unmeasured HPV statuses which can be 0 or 1). Therefore, the transition probability between states with known HPV statuses is calculated as three-fold sum over all combinations of HPV statuses in these three unmeasured states.