Measurement of the membrane potential in small cells using patch clamp methods

Abstract

The resting membrane potential, E_m, of mammalian cells is a fundamental physiological parameter. Even small changes in E_m can modulate excitability, contractility and rates of cell migration. At present accurate, reproducible measurements of E_m and determination of its ionic basis remain significant challenges when patch clamp methods are applied to small cells. In this study, a mathematical model has been developed which incorporates many of the main biophysical principles which govern recordings of the resting potential of “small cells”. Such a prototypical cell (approx. capacitance, 6 pF; input resistance 5 GΩ) is representative of neonatal cardiac myocytes, and other cells in the cardiovascular system (endothelium, fibroblasts) and small cells in other tissues, e.g., bone (osteoclasts) articular joints (chondrocytes) and the pancreas (β cells). Two common experimental conditions have been examined: (1) when the background K⁺ conductance is linear; and (2) when this K⁺ conductance is highly nonlinear and shows pronounced inward rectification. In the case of a linear K⁺ conductance, the presence of a “leakage” current through the seal resistance between the cell membrane and the patch pipette always depolarizes E_m. Our calculations confirm that accurate characterization of E_m is possible when the seal resistance is at least five times larger than the input resistance of the targeted cell. Measurement of E_m under conditions in which the main background current includes a markedly nonlinear K⁺ conductance (due to inward rectification) yields complex and somewhat counter-intuitive findings. In fact, there are at least two possible stable values of resting membrane potential for a cell when the nonlinear, inwardly rectifying K⁺ conductance interacts with the seal current. This type of bistable behavior has been reported in a variety of small mammalian cells, including those from the heart, endothelium, smooth muscle and bone. Our theoretical treatment of these two common experimental situations provides useful mechanistic insights, and suggests practical methods by which these significant limitations, and their impact, can be minimized.

Introduction

Accurate and reproducible intracellular recordings of transmembrane potentials require recording methods which cause only minimal short or long term changes to the target cell. In the case of conventional electrophysiological work applied to multicellular tissues or relatively large cells, this technical challenge has been met satisfactorily. The combination of fabricating microelectrodes with very small tip diameters, and which can be filled with highly conductive solutions (e.g., 3 M KCl) has been proven to be effective. However, it is now recognized that this approach for measuring the resting potential cannot yield satisfactory results when cells selected for study are very small (e.g., 5–10 µm diameter; total capacitance 6 pF). These intrinsic properties result in these cells exhibiting large input resistances (>5 GΩ) and apparently having variable resting potentials. In spite of this, the whole cell patch clamp method is often relied upon for biophysical studies in many different types of small cells. It is essential therefore, to further understand the main principles which govern the validity and the reproducibility of measurements of resting membrane potential using patch clamp methods.

To be effective, the patch microelectrode needs to attain and maintain access to the intracellular milieu in such a way that the resistance between the surface of the glass pipette (“seal resistance”) and the target cell membrane is much larger than the input resistance of the cell.^1–3 In the absence of this (e.g., seal resistance being at least five times higher than the input resistance of the single cell) significant “seal leakage currents” develop in response to applied voltage gradients during all measurements of conventional electrical activity and also during voltage clamp experiments. These seal currents can significantly alter recorded values of the membrane potential. Equally importantly, they add a “leak” component to transmembrane current recordings in voltage clamp experiments. This seal leak current can significantly alter or even completely eliminate very important biophysical properties of the intrinsic ion transport mechanisms, such as the negative slope of an inward rectifier current-voltage relation.⁴ Details of the properties of the current-voltage or ion transfer relations are often the focus of electrophysiological/biophysical investigations. As a result, an improved understanding of the influence of artefactual leak currents on recorded currents is essential for correct interpretation of experimental data.

These limitations and technical challenges have been recognized by a number of previous investigators. For example Hagiwara and coworkers⁵ demonstrated that these leakage currents must be accounted for even in studies involving heterologous expression of potassium channels in exceptionally large cells (frog oocytes). They demonstrated that the defining features of the ion transport mechanism of a strongly inward rectifying background potassium current could be obscured completely by this recording artefact. Their work also revealed that the presence of the seal leakage current is a plausible reason for the observation that there were two apparently quite different, and yet stable, resting membrane potentials. Similar investigations^4,6,7 using enzymatically isolated single mammalian cells in which whole-cell patch clamp techniques were applied have also demonstrated that even with much smaller seal leakage currents the reliability of recordings of resting membrane potential can be compromised.^2–4 These artefacts can also significantly alter, if not obscure, very important features of ion transport mechanisms in these mammalian “target” cells.

Previous work from our own laboratory has drawn attention to this type of technical challenge when attempting to make recordings from single cells (myocytes) from the pacemaker region of the heart,⁸ from conduction system Purkinje fibres or cells,⁶ or the atrium of mammalian hearts.⁹ Recently our group and others have recognized (and appropriately dealt with) this limitation when attempting to make semi-quantitative measurements from single cells isolated from selected cardiovascular tissues and cells. For example, recordings from fibroblasts,¹⁰ endothelial cells,¹¹ or pericytes¹² and smooth muscle myocytes from resistance vessels¹³ can be very difficult to interpret without full recognition of this technical limitation.

In all of these cases, and in analogous electrophysiological work on single cells from other tissues e.g., osteoclasts,¹⁴ these factors are also important. A major reason is that the resting membrane potential is generated by a background K⁺ current which is highly nonlinear. This type of ion transport mechanism has been denoted a strong inward rectifier: that is, a potassium selective ion transport mechanism which when characterized in terms of its current-voltage relationship shows both inward rectification and a significant region of negative-slope conductance.^15–17

Previous examination of the errors in patch clamp analysis have focused on the liquid junction potential generated at the patch electrode-cell interface¹⁸ and the leakage on “shunt” resistance due to the patch electrode.^2,3 Other studies have noted that the recorded membrane potential for fibroblasts has a large variability.^7,10 The apparent instability of the resting potential E_m in cardiac Purkinje fibres and smooth muscle (resistance vessels) myocytes has been noted.^6,19–22

In this study, we have developed a mathematical model based on equivalent circuits of (i) the main trans-membrane ionic transport properties of a single isolated small cell and (ii) the circuit elements which represent the patch microelectrode and current recording amplifier. These simulations computed the stable value(s) of the resting membrane potential of the model or target cell. Transmembrane ionic currents and membrane potentials were calculated under two different sets of assumptions: (1) the model cell “expressed” only one time and membrane potential independent “background” K⁺ current which had an ohmic or linear ion transfer mechanism or I–V curve; and (2) the predominant background K⁺ conductance was highly nonlinear and exhibited marked inward rectification.

This computational work clearly illustrates the major limiting principles of very frequently encountered settings for patch clamp recordings. Our simulations also demonstrate plausible mechanisms by which a number of different single cells from the cardiovascular system can be characterized as having two stable but significantly different resting potential values. Finally, we note that an improved understanding of these limiting technical conditions, which are intrinsic for many small isolated mammalian cells, can suggest possible ways of reducing these artefacts.

Results

Simulation of E_m measurements assuming a linear background K⁺ current, I_K.

The results of a set of simulations based on the assumption that the cell expresses only a single, linear K⁺ current are shown in Figure 1. In the absence of “leak” currents produced by introduction of the patch microelectrode, the zero-current potential, V₀, is the same as the K⁺ Nernst potential, −85 mV. However, the presence of the seal “leak” currents results in depolarization of the cell membrane. Note that the resting membrane potential depolarizes to such a level where the K⁺ “leak” current and seal leak current are equal in magnitude (but opposite in sign). This membrane potential recording “configuration” thus closely resembles a classical “voltage-divider”, with the resting potential of the cell given by the expression:

$$V_0=\frac{E_K{R}_S+E_S{R}_K}{R_K+R_S}$$ (Eqn. 1)

(Note that the seal reversal potential, E_s, has been set to zero in these simulations). The recording amplifier will report this depolarized potential as the zero-current potential, V₀. Figure 1A shows the effects of several discrete values of seal resistance on the zero-current potential. A six-fold difference between the cell resistance (5 GΩ) and an “excellent” seal resistance (30 GΩ) results in an “error” of +12 mV in the zero-current potential, whereas a “poor” seal resistance (3 GΩ) depolarizes the cell by 53 mV compared with its “true” value. Figure 1B illustrates the relationship between seal resistance, R_s and zero-current potential, V₀, over a wide range of R_s values. Note that (as demonstrated previously) only when R_s is significantly larger than the input resistance, R_IN, does the recorded zero-current potential E_m approximate the “true” resting membrane potential, E_K. For very low resistance seals the zero-current potential approaches the reversal potential of the seal current, assumed to be 0 mV in these simulations.

Figure 1.

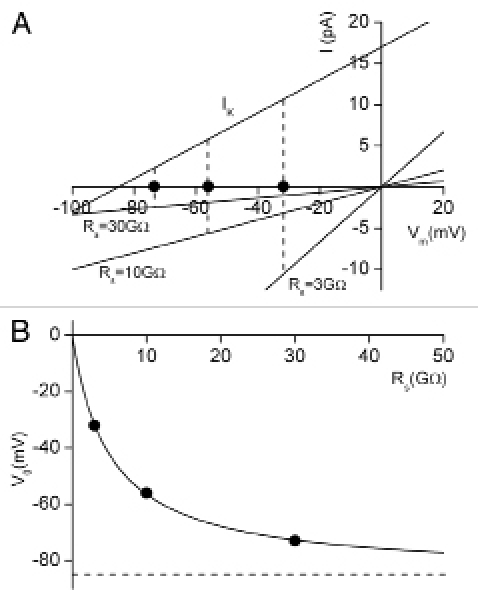
Simulations of apparent resting membrane potential assuming that only a linear background K⁺ current, I_K, contributes, and a conductance of 200 pS, corresponding to cell input resistance of 5 GΩ. (A) shows the current-voltage relation for I_K and the seal currents for an “excellent” seal: 30 GΩ; a “good” seal: 10 GΩ; and a “poor” seal: 3 GΩ. In both current-clamp and voltage-clamp configurations, zero current through the patch electrode corresponds to the condition where the current through the cell membrane is matched by the current through the patch electrode seal. For the three seal conditions, this occurs at membrane potentials of −73, −56 and −32 mV. (B) shows the dependence of the zero-current potential, V₀, on the seal resistance, R_s, for a wide range of resistances. Note that under these conditions, as the seal resistance increases, V₀ approaches E_K, the true resting potential of this model cell. The three specific values of R_s used in (A) are denoted by black dots.

In constant current recording mode with zero current through the patch microelectrode, I_e = 0, the electrode resistance R_e does not affect the recorded value of membrane potential. There is, however, current flowing through the seal. We denote this as I_s. For negative membrane potentials this is an inward current, I_s < 0. This current then exits the cell, and the recorded zero-current potential is offset from the real or actual resting potential of an identical but non-attached cell. Note that the simulations shown in Figure 1 indicate that for recordings from high input resistance cells, even seal resistances that would be considered to be entirely acceptable (e.g., 10 GΩ) still can produce a very significant difference between the true resting membrane potential of the cell, and that recorded with the patch clamp electrode in situ.

Simulations of E_m when an inward rectifying K⁺ current, I_K1 is responsible for E_m.

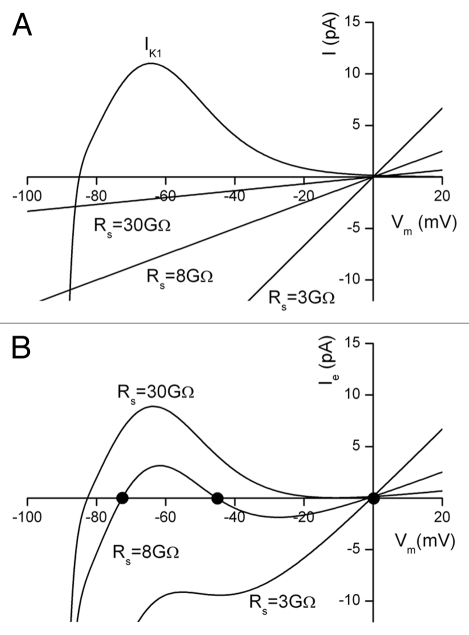
The experimental manoeuvre of “attachment” of the patch electrode to the cell can cause a seal “leakage” current which depolarizes the cell by shifting the zero-current membrane potential to more depolarized potentials. For the linear K⁺ current cell model shown in Figure 1 the depolarization is monotonically related to seal resistance. However, when the linear K⁺ current model is replaced by the non-linear inwardly rectifying K⁺ current, I_K1, the relationship between seal resistance and zero-current potential is more complex. Figure 2 shows the results of a simulation done using a cell model in which the resting membrane potential is generated entirely by an I_K1-like background K⁺ current. Note that the I_K1 current-voltage relation has a region of “negative-slope conductance”; this current exhibits an outward peak at −64 mV. At membrane potentials more positive than this the outward current decreases. Consequently the influence of the magnitude of the seal resistance on zero-current potential becomes more important at depolarized membrane potentials. Unlike the linear K⁺ current model in which depolarization of the zero-current potential is a simple monotonic function of the ratio of cell resistance to seal resistance, introduction of the very non-linear I_K1 current into the model results in more than one value of zero-current potential, even with a fixed value of R_s. Note that zero-current potentials near 0 mV can be found, even for high resistance seals (Fig. 2B).

Figure 2.

Simulation of the effect of leakage current through the seal resistance in a cell in which a nonlinear background K⁺ current, I_K1 is assumed to be the sole mechanism for generation of V_m. (A) shows the three linear current-voltage relations due to the seal current, assuming three different seal resistances (30 GΩ, 8 GΩ and 3 GΩ). Note that the background K⁺ current has a peak outward current of 11 pA at −64 mV, and a reversal potential of −85 mV. (B) shows the patch electrode current, I_e or total net current (I_K1 + I_seal), as a function of membrane potential. With R_s = 30 GΩ, zero current in the patch electrode occurs at V_m = −82 mV. With R_s = 8 GΩ, zero current occurs at three different membrane potentials: −72.5, −45 and −2 mV (highlighted with black dots). Note that with R_s = 3 GΩ, zero current only occurs close to the reversal potential for the seal at V_m = −0.5 mV. As such, the recording of the resting potential of this small cell is dominated completely by the recording “artefact” due to the interaction of the seal current and the background K⁺ current.

Simulations based on a cell model consisting of an inward rectifying K⁺ current, I_K1, Na⁺/K⁺ pump current, I_NaK and background Na⁺ current, I_bNa.

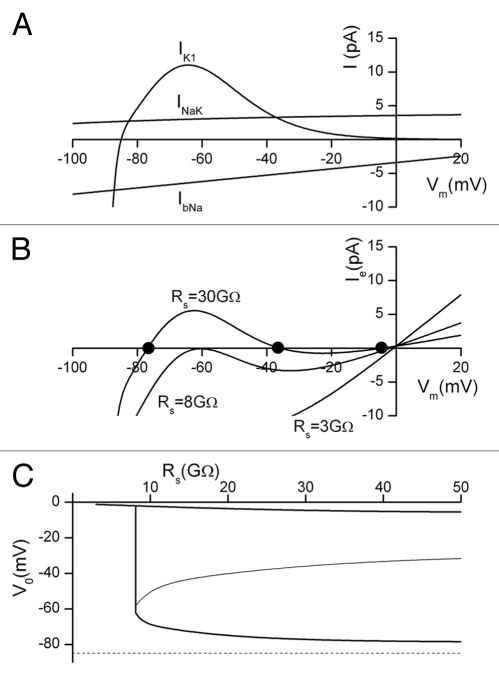
The final set of simulations was done under somewhat more “realistic” conditions with respect to the known ionic mechanisms responsible for the resting potential in mammalian cells. An electrogenic current due to the Na⁺/K⁺ pump and a linear, time-independent background Na⁺ current were added to the inward rectifying K⁺ current I_K1.

The pump current I_NaK and the background current I_bNa are both much less voltage sensitive than I_K1, as shown in Figure 3A. I_NaK is outward over the entire membrane potential range of interest (−90 to +20 mV), while the Na⁺ background current I_bNa is inward over the same membrane voltage range. These currents contribute to the net current, along with I_K1 and leakage current through the patch seal, as illustrated in Figure 3B for three different values of R_s. Compared with the calculations shown in Figure 2, the net membrane current is reduced, and depolarization of the model cell is more sensitive to the magnitude of the seal resistance than a cell in which E_m depends only on I_K1. For example, in the model output shown in Figure 2, assuming a seal resistance R_s of 8 GΩ, there are three distinct values of membrane potential at which there is zero net current: −72, −45 and −2 mV respectively. However, if I_NaK and I_bNa are added to the cell model, as shown in Figure 3B, a seal resistance of 8 GΩ results in only two membrane potentials at which there is zero net current, and these are at −61 and −2 mV respectively.

Figure 3.

Simulation of the effect of leakage current through the patch microelectrode seal resistance in a cell which expresses a realistic combination of time independent or background currents: (i) a nonlinear K⁺ current, I_K1, (ii) a Na⁺/K⁺ pump current, I_NaK and (iii) a Na⁺ current, I_bNa. (A) shows the current-voltage relations for each of I_K1, I_NaK and I_bNa. (B) shows the patch electrode total current, I_e, as a function of membrane potential, for three different values of seal resistance R_s. Note that for R_s = 30 GΩ there are three zero-current potentials: −77, −36 and −4.5 mV (black dots). For R_s = 8 GΩ, the zero-current membrane potentials are −61 and −2.5 mV. At R_s = 3 GΩ, zero current only occurs when the membrane potential depolarizes to V_m = −1 mV. (C) shows the relationship between V_o and R_s for the three-conductance cell model in (A). For R_s ≥ 8 GΩ, the cell exhibits 3 distinct values of V_o, while for R_s < 8 GΩ, there is only one, very deoplarized value. There is a very sharp “discontinuity” in the V_o-vs.-R_s relation in the vicinity of R_s = 8 G. The dotted line represents the true value of resting potential at −85 mV.

Stability and sensitivity of the apparent resting potential.

During experimental recording, the seal resistance can be expected to change due to small thermal and mechanical artefacts. This in turn causes fluctuations in the reported resting potential of the cell. For simulations with a linear K⁺ current the sensitivity of the zero current potential to this type of seal resistance change is governed by the gradient of the R_s-V₀ curve shown in Figure 1B. At high seal resistances, the gradient is small and any fluctuation in R_s will produce only a small fluctuation in V₀. At lower values of seal resistance, the gradient is larger and fluctuations in R_s can give rise to quite large transient changes in the apparent resting potential, V₀. In contrast, for simulations which include the nonlinear I_K1, together with I_NaK and I_bNa, the zero current potential(s) is related to R_s in a much more complex fashion. This is shown in Figure 3C. This plot shows that for all values of R_s ≥ 8 GΩ, the cell exhibits three zero current potentials, one of which is close to 0 mV, regardless of the magnitude of R_s. The magnitude of the other two potentials diverge as R_s is increased, with one of the stable values of membrane potential closely approaching the “true” membrane potential, while the other decreases. It is also evident from Figure 3C that the zero current potentials for R_s ≥ 8 GΩ change relatively smoothly and slowly with changes in the magnitude of R_s. However, there is a very steep “discontinuity” in the V_o-vs.-R_s relationship near R_s = 8 GΩ, where very small fractional changes in the magnitude of R_s can alter V_o by about 60 mV. That is, the apparent E_m can change from values approximating the “true” resting potential of the cell, to nearly complete depolarization, and vice versa. Hence, exactly where the apparent “resting potential” of the cell occurs on the V_o-vs.-R_s plot depends critically on the relationship between the magnitudes and voltage dependence of the membrane currents, and the magnitude of the seal resistance. In summary, during an experimental recording with a relatively low seal resistance from a small cell in which these three conductances produce the membrane current, the reported resting potential may appear relatively steady during the recording, but the resting potential will likely be far from the true physiological value.

Simulations which include the nonlinear inward I_K1 current show the existence of three zero-current potentials for R_s > 8 GΩ (Figs. 2B and 3B). The intermediate value of V₀ occurs within the “negative slope” region of the I_K1 curve. Consequently, small perturbations of the membrane potential will generate a membrane current which tends to increase the depolarization. In fact, the membrane potential will swing to one of the two stable zero current potentials. In principle, during an experimental recording, the reported resting potential may initially be close to the true physiological value. However, any depolarizing influence which (even briefly) takes the membrane potential positive to the unstable V₀, will strongly depolarize the cell and this depolarized value of E_m will be maintained or appear stable.

In experiments which are aimed at determining the ionic basis for the resting potential, it is often necessary to increase and decrease [K⁺]_o from its normal value, approximately 5.4 mM. In the cases illustrated in Figures 2 and 3, this can give rise to a very complex set of changes in the current generated by the nonlinear K⁺ conductance I_K1. These changes are well-described in the experimental literature²³ and this phenomenon is often referred to as the [K⁺]_o-dependent crossover. This is illustrated in Figure 4, using the assumptions identical for those on which the calculations in Figure 3 were based. These calculations illustrate an example of the difficulty in attempting to accurately measure resting potential in low [K⁺]_o. Under this circumstance, the input resistance of the cell can increase and the current through the seal resistance can markedly depolarize the cell.

Figure 4.

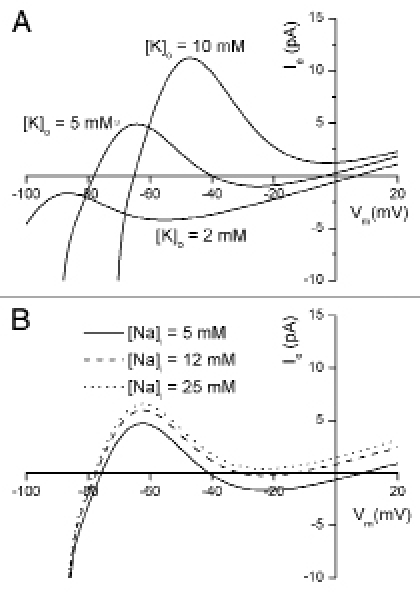
Simulation of experimental manoeuvres, changing external [K⁺] or internal [Na⁺], which may reduce “seal leakage error”. Patch electrode current, I_e are plotted as a function of membrane potential, V_m at selected [K⁺]_o and [Na⁺]_i levels. The same set of membrane currents as in Figure 3 was used; a (constant) seal resistance of 30 GΩ is assumed. (A) demonstrates that increasing [K⁺]_o from a physiological level (5 mM) results in a “cross-over” of the I–V relations, i.e., the peak actual current increases and shifts to more positive membrane potentials. At [K⁺]_o of 10 mM or higher, the zero current potential has a single value at approximately −70 mV, and the bistable nature of the apparent resting potential (as shown in Fig. 3) is not observed. In contrast, at [K⁺]_o of 2 mM or less, the nonlinear I_K1 current is obscured by the dominant Na⁺/K⁺ pump current, I_NaK, and the background Na⁺ current, I_bNa, both of which are linear. The only apparent resting potential is at +7 mV. (B) shows that increasing internal [Na⁺] of the cell increases outward Na⁺-K⁺ pump current, which results in more negative zero-current potentials [Na⁺]_i levels of 25 mM or larger result in a single value for the zero current potential at approximately −80 mV.

Discussion

These calculations provide further basis for identifying the main electrophysiological paradigms which determine the ability of the conventional patch clamp technique to record valid membrane potential values. As has been demonstrated previously, the fundamental requirement is that the seal resistance formed between the tip of the glass “patch” microelectrode and the plasmalemma of the target cell must be at least 5–10 times larger than the value of the input resistance of the cell.^2–4 This can be quite difficult to achieve when isolated single myocytes from e.g., neonatal hearts are studied, as these cells typically have input resistances in the 1–9 GΩ range. A consequence of this is that conventional microelectrodes are inadequate, even under optimal conditions, as the typical seal resistances achieved with this recording methodology is 10–50 MΩ. Patch clamp electrodes offer an improvement since multi-gigaohm seal resistances can be obtained, but even this is not wholly adequate.

Figures 2 and 3 provide novel insights into the consequences of this technical limitation under circumstances in which these or other small cells express a K⁺ conductance which exhibits marked inward rectification, for example, when the K⁺ channel isoforms K_ir2.1 or 2.2 are responsible for the predominant background K⁺ current.^16,17 In this setting, leakage currents through the seal resistance can (and often do) result in the apparent resting potential having two distinct and significantly different values. This is not a new observation. Both cardiac and skeletal muscle electrophysiologists described this phenomenon 30 years ago, based on experiments with conventional high resistance microelectrodes for studies of the resting potential of cardiac Purkinje fibers or of skeletal muscle fibers.^5,20 In these cases the low seal resistance resulted in seal current flow which depolarized the preparation from the expected resting potential, (very near the K⁺ electrochemical equilibrium potential), to a value of approximately −40 mV. This same principle frequently manifests itself when patch microelectrodes are applied in an attempt to measure the resting membrane potential of small cells which have very high input resistances. The most plausible interpretation is that these cells express mainly a prominent inwardly rectifying background potassium current at potentials near their resting potential, as opposed to actually having two characteristic “resting” membrane potentials. This bistable phenomenon is much more commonly observed under conditions where extracellular potassium, [K⁺]_o, is relatively low (4 mM),²³ or has been reduced as a planned experimental manoeuvre. As shown in Figure 4 (and demonstrated repeatedly in previous experimental papers) reduction in [K⁺]_o results in a characteristic (but complex) change in the current-voltage relationship for this inwardly rectifying K⁺ conductance.²³ Lowering [K⁺]_o effectively increases the input resistance of the cell in a range of membrane potentials near the K⁺ electrochemical equilibrium potential.

There are a number of important physiological settings in which these considerations become essential for proper interpretation of experimental findings. It is well known that either during normal embryonic or neonatal development the density of a small number of K⁺ channels changes quite significantly. In the heart there is virtually no expression of K_ir2.1 at very early stages of development. Later in development expression of K_ir2.1 increases and this outward current predominates at membrane potentials within the diastolic or resting range.²⁴ Accordingly, when studying ventricular myocytes one would expect to be able to record predictable and accurate resting membrane potentials only at a late stage of development. This same underlying principle is now known to apply in previous studies of the membrane potential in the adult heart when myocytes from atrium, Purkinje tissue and ventricle are compared.^6,9 The magnitude of I_K1 is much smaller in atrium and Purkinje tissue than in ventricle. Our simulations suggest that in conditions where the magnitude of I_K1 is relatively small, there may be more than one zero-current potential, and accordingly, there are a number of reports of bistable “resting membrane potentials” in atrium and Purkinje cells. A similar pattern of behavior has been reported when myocytes from the ventricle are studied in low [K⁺]_o, which reduces the magnitude of I_K1.²³ A plausible reason for these phenomena is demonstrated in Figures 3 and 4.

It is also known that the so-called “strongly inwardly rectifying” K⁺ channels e.g., K_ir2.1, 2.2 can be modified as a consequence of common disease e.g., diabetes or hypertension.^25,26 Direct genetic regulation of these channels can also contribute to cardiac arrhythmias.^27,28 In some of these cases it is recognized that these electrophysiologic changes result from the influence of this type of K⁺ current on (i) the resting potential and (ii) cell-to-cell communication.^29–31

It may be possible to carry out experimental manoeuvres which minimize the chances that a combination of nonlinear background K⁺ currents and low seal resistance in patch clamp experiments may generate anomalous results. Thus, any manoeuvre which results in additional net outward current will reduce (and may prevent) the depolarization of membrane potential resulting from the inward current through the seal resistance. One practical manoeuvre which achieves this is to include 10–15 mM Na⁺ in the recording patch pipette.¹⁰ Equilibration of such [Na⁺]i activates the Na⁺/K⁺ pump and generates a net outward current. Second, in some experimental situations it is possible, (but perhaps not advisable), to record from 2–4 cell clusters which are electrically coupled and therefore behave as a syncytium. This effectively reduces the input resistance of the preparation (i.e., increases the net membrane currents) in relation to the seal resistance and this can stabilize the apparent resting membrane potential.^3,15,32 Finally, for any given patch microelectrode method it may be possible to utilize the principles of glass surface electrochemistry to improve the seal resistance in conventional patch clamp recordings. Some of these principles form important concepts and components in the emerging planar “patch-on-a-chip” semi-automated electrophysiological recording platforms.

Methods

In this study the electrical interactions between a small prototypical cell and a patch recording microelectrode are modeled at three different levels of complexity. The architecture of the models and the equations representing the selected transmembrane currents have been defined using the modeling language CellML and the system has been solved using the Physiome CellML Environment (PCEnv0.6 University of Auckland).³³ These models exploit the modularity of CellML, by defining the electrode, the seal resistance and the separate membrane currents as individual CellML components.

This approach is intended to facilitate reuse, as recommended by the CellML development group.³³ The cell, patch microelectrode and associated electronic amplifier, and the microelectrode-to-cell seal are modeled as a coupled system in the whole-cell recording configuration (Fig. 5). While applicable to other recording modalities such as “patch on a chip” methods,³⁴ the scale of the electrode parameters have been chosen to be representative of conventional glass patch pipettes. The currents have been represented as absolute values, instead of the more typical normalization to current densities. This obviates current scaling between the electrode and cell components, and it facilitates using the electrode and electrode-cell seal components without modification in other cell models.

Figure 5.

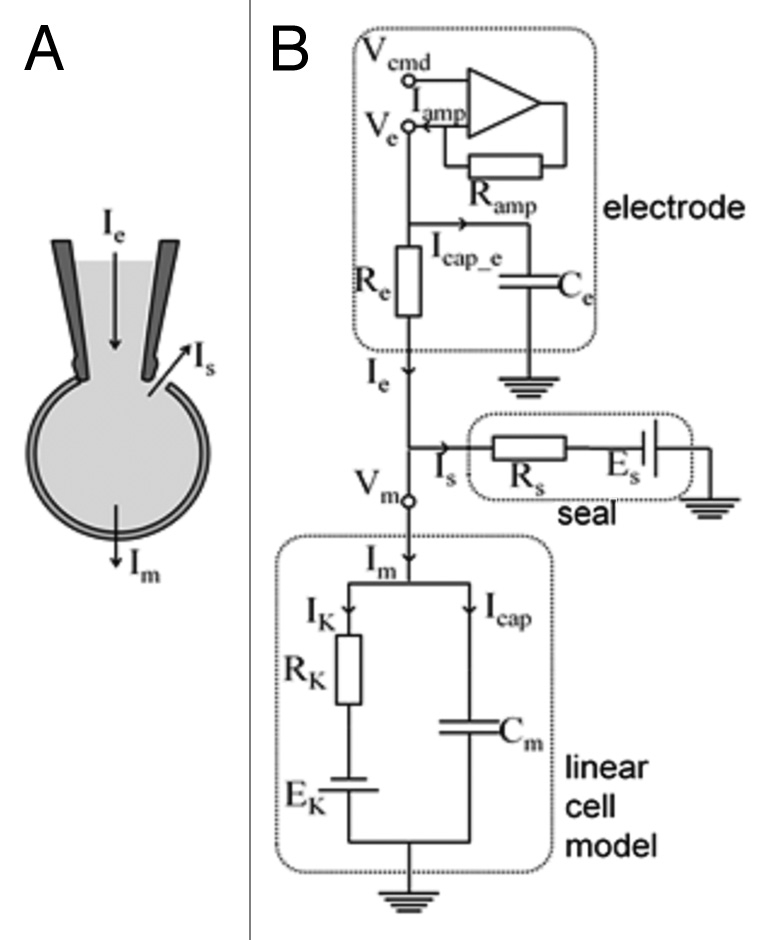
Equivalent electrical circuit for a mammalian cell coupled to a patch clamp electrode and recording amplifier. (A) illustrates the patch electrode attached to a cell and shows the total (pipette) current, I_e, the seal current, Is, and the membrane current, I_m. (B) shows the microelectrode with electrode potential, Ve and patch electrode resistance and capacitance, R_e and C_e. The “seal” element is simulated by a resistance (R_s) and an emf (E_s); in these simulations E_s is assumed to be 0 mV. For voltage-clamp simulations the amplifier is explicitly represented. In the simulations in this paper the patch microelectrode and electrode seal resistances are incorporated into (i) the model cell expressing a single linear K⁺ membrane current, as shown; or (ii) to a model cell comprising an inward rectifier K⁺ current, I_K1, a Na⁺/K⁺ pump current, I_NaK, and a background Na⁺ current, I_bNa.

Patch microelectrode.

The typical glass microelectrode used for patch clamp recordings can exhibit a significant series resistance. This is mainly due to the narrow, fluid filled taper to a fine tip from the lumen of the shank. The glass shank itself is an insulator and can represent a significant capacitance. However, the geometry of the microelectrode concentrates the resistance and the capacitance very near the tip. The microelectrode is, therefore, modeled as a single series resistance and parallel capacitance as shown in Figure 5. In this study the electrode parameters were selected as: electrode resistance, R_e = 10 MΩ and electrode capacitance, C_e = 5 pF.

In the “current-clamp” configuration, the current entering the electrode from the amplifier, I_amp, was held at the command current level, which was zero current in these simulations. The model was also run in a voltage-clamp configuration in which I_amp was calculated as a result of the difference between the command potential and the microelectrode potential. This calculation assumed a simple amplification circuit with properties: feedback resistance, R_amp = 1 GΩ; and open loop gain, A = 10,000.

Patch microelectrode to cell seal resistance.

The glass microelectrode is assumed to “seal” with the surface membrane forming, a very large, but not infinite resistance between the interior and the exterior of the cell. Hence current can “leak” between the external medium and the interior of the cell via this “seal”. For these simulations, the electrode-to-cell seal “leakage” current (I_s) is represented as a linear current:

$$I_0=\frac{1}{R_S}(V_m)$$ (Eqn. 2)

where R_s is the overall “seal resistance”, and V_m is the cell membrane potential. Because the seal leakage current is carried non-selectively by both cations and anions in the extra- and intracellular media, the seal leakage current is assumed to reverse at a membrane potential of zero. In most of these simulations, R_s has values of 3, 8, 10 or 30 GΩ. Seal resistances in this range are typical of tight “giga-seals”, which are considered to range from relatively “poor” (3 GΩ) to “excellent” (30 GΩ).

Linear background K⁺ current (I_K) assumption.

Our initial representation of the membrane properties of the cell assumed only a linear K⁺ current as responsible for the resting potential. The I–V relation of this current was assumed to be omhic, namely:

$$I_K=\frac{1}{R_K}(V_m-E_K)$$ (Eqn. 3)

The conductance of this K⁺ current pathway was 200 pS, which corresponds to an input resistance of the cell of R_K = 5 GΩ. E_K is the Nernst potential for K⁺, which was set at −85 mV. The K⁺ conductance of this cell was assumed to exhibit no time- or voltage-sensitivity. This very simple model can illustrate the magnitude of the influence of the seal resistance on recorded resting membrane potential. The equivalent circuits of the electrode, the electrode-to-cell seal, and the cell membrane K⁺ current were combined into a complete circuit model as shown in Figure 5.

More complex representations of the ionic currents in small cells included several types of time-independent or “background” currents. Three such currents were: (i) an inwardly rectifying K⁺ current (I_K1); (ii) a current due to an electrogenic Na⁺-K⁺ pump (I_NaK); and (iii) a “background” Na⁺ current (I_bNa). Thus, net membrane current, I_m, is given by the equation:

$$I_m=I_{K1}+I_{NaK}+I_{bNa}+C_m\frac{d{V}_m}{dt}$$ (Eqn. 4)

A transient current due to the cell capacitance charging/discharging (C_mdV_m/dt) was also included for these calculations. Thus, the current through the patch microelectrode, which is the current recorded by the amplifier, is given by the sum of membrane and seal leak currents:

• I_e = I_m + I_s

Inward rectifier K⁺ current (I_K1).

The I_K1 inward rectifier K⁺ current is highly nonlinear. This current has been identified in many small mammal cells, including myocytes, fibroblasts, endothelial cells and Purkinje cells from the mammalian cardiovascular system.

The formulation for this current used by MacCannell et al.³⁵ and by ten Tusscher et al.³⁶ was employed:

$$I_{K1}=g_{K1}{\left(\frac{{\left[K^{+}\right]}_o}{5.4}\right)}^{\frac{1}{2}}\frac{{\alpha }_{K1}}{{\alpha }_{K1}+{\beta }_{K1}}\left(V_m-E_K\right)$$ (Eqn. 5)

where the voltage-dependent parameters are defined as

$${\alpha }_{K1}=\frac{0.1}{1+e^{0.06\left(V_m-E_K-200\right)}}$$ (Eqn. 6)

and

$${\beta }_{K1}=\frac{3e^{0.0002\left(V_m-E_K+100\right)}+e^{0.1\left(V_m-E_K-10\right)}}{1+e^{-0.5\left(V_m-E_K\right)}}$$ (Eqn. 7)

The ten Tusscher formulation³⁶ of I_K1 was based on current magnitudes appropriate for a human ventricular myocyte with a membrane capacitance of about 100 pF. Accordingly, the I_K1 conductance parameter, g_K1 was scaled to correspond to an approximately 17-fold smaller 6 pF cell, with g_K1 = 32.43 nS.

Electrogenic Na⁺/K⁺ pump current (I_NaK).

Our model incorporated an electrogenic Na⁺-K⁺ pump current with a 3Na⁺-2K⁺ stoichiometry. The voltage and concentration sensitivity of this pump was based on a formulation previously developed in this laboratory for atrial myocytes from rabbits,³⁷ and humans.^29,38 Na⁺-K⁺ pump current, I_Na,K, was given by:

$${{\rm I}}_{NaK}={\overline{{\rm I}}}_{NaK}\left(\frac{{\left[K^{+}\right]}_O}{{\left[K^{+}\right]}_O+K_{mK}}\right)\left(\frac{{\left[N{a}^{+}\right]}_i^{1.5}}{{\left[N{a}^{+}\right]}_i^{1.5}+K_{mNa}^{1.5}}\right)\frac{V_m-V_{rev}}{V_m+200}$$ (Eqn. 8)

where [K⁺]_o and [Na⁺]_i are external K⁺ and internal Na⁺ concentrations, respectively, and V_rev is the reversal potential of the pump current (−150 mV in these simulations). K_m,K and K_m.Na are binding constants with values of 1.0 mmolL⁻¹ and 11.0 mmolL⁻¹, respectively. The magnitude of the current scaling parameter Ī_NaK used for human atrial myocytes^29,38 was scaled to correspond to a 6 pF cell, with Ī_NaK = 8.17pA.

Background Na⁺ current (I_bNa).

A linear background Na⁺ current, I_bNa, was incorporated. The magnitude of the current was adjusted such that net Na⁺ flux due to this current and the Na⁺-K⁺ pump current was zero near the resting potential of the cell, which was about −85 mV. This requirement resulted in a conductance of g_bNa = 47.0 pS. Background Na⁺ current was given by:

$${{\rm I}}_{bNa}=g_{bNa}\left(V_m-E_{Na}\right)$$ (Eqn. 9)

Computations.

Solution of the equations used the default PCEnv integration routine, a backwards Euler algorithm with 1 ms maximum time step. The I–V curves were created by simulating a voltage clamp protocol with 0.1 mV steps from −100 mV to +100 mV. There is a small voltage drop across the electrode resistance, R_e. In most experimental recordings from small cells this voltage drop is either negligible or is compensated by the amplifier, and therefore has been ignored in these simulations. The I–V curves shown in the Figures illustrate either the transmembrane currents, or alternately, the total current through the patch electrode, I_e, which is the sum of the transmembrane currents and the seal current.