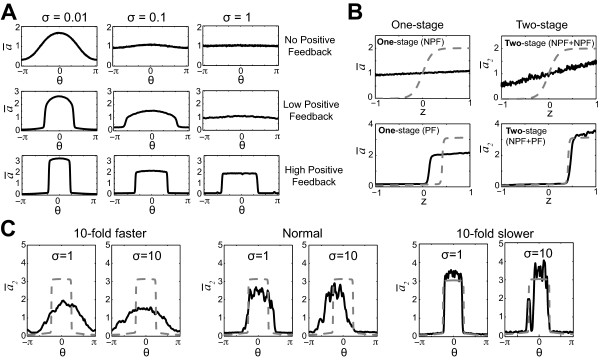
Figure 2.
Exploring noise-filtering strategies. (A) Increasing the positive feedback improved the extent of polarization at higher noise levels. 2D simulations were performed on the model in which the strength of the positive feedback ranged from none (k1 = 0) to low (k1 = 10, h = 2) to high (k1 = 10, h = 8). For a given gradient (Lmid = 1, Lslp = 0.01 μm-1), higher positive feedback produced stronger polarization at higher levels of noise. The time-average of the polarity variable a(ā) with respect to θ is plotted. (B) Adding a filtering module improved polarization. In the top row, there was a single NPF (no-positive-feedback) module compared to two NPF modules in series. In the second row, there was a single PF (positive feedback) module compared to a two-stage arrangement of a NPF module followed by a PF module (NPF+PF). The extra stage resulted in improved polarization. Dashed gray lines represent polarization in the absence of input noise (1D simulations with Lslp = 0.01 μm-1, σ = 0.1). (C) Slower dynamics produced more accurate and effective polarization. In a two-stage NPF+PF model, we scaled the parameters either 10-fold faster or 10-fold slower in 2D simulations (Lslp = 0.01 μm-1). We plotted the spatial distribution of the output of the second stage ā2 for two values of σ.