Abstract
Two-gene classifiers have attracted a broad interest for their simplicity and practicality. Most existing two-gene classification algorithms were involved in exhaustive search that led to their low time-efficiencies. In this study, we proposed two new two-gene classification algorithms which used simple univariate gene selection strategy and constructed simple classification rules based on optimal cut-points for two genes selected. We detected the optimal cut-point with the information entropy principle. We applied the two-gene classification models to eleven cancer gene expression datasets and compared their classification performance to that of some established two-gene classification models like the top-scoring pairs model and the greedy pairs model, as well as standard methods including Diagonal Linear Discriminant Analysis, k-Nearest Neighbor, Support Vector Machine and Random Forest. These comparisons indicated that the performance of our two-gene classifiers was comparable to or better than that of compared models.
Keywords: Cancer, Classification, Gene Expression Profiling, Information Entropy, Computational Biology
1 Introduction
Many studies have made it a growing consensus that to deal with high-dimensional gene expression data, simple classifiers often have substantial advantages over complicated ones [1–7]. One advantage is that simple classifiers often have better classification performance but lower computational cost than complex classifiers. Another advantage is that simple classifiers are more interpretable and applicable compared to complex classifiers because they are often involved in a small number of genes and simple classification rules. As a typical representative of simple classifiers, the two-gene classifier has attracted an increasing interest [8–17]. Among them, the top-scoring pair(s) (TSP) classifier classifies phenotypes according to the relative expression of a pair of genes as contributes to its two advantages: first, it avoids over-fitting by eliminating specific parameter tuning; second, it is not affected by normalization issues [8–9]. In [17], the authors proposed gene-pair based methods to select gene sets which well distinguished two classes. In [3], the authors screened a small number of informative gene pairs on the basis of their depended degrees proposed in rough sets by which the decision rules were induced to classify phenotypes classes. These two-gene classification algorithms indicated that gene pairs in combination might better discriminate different classes than individual genes due to gene interactions.
Although class prediction might be improved by taking advantage of the gene-interaction information, the relevant algorithms were often time-consuming. Moreover, these algorithms were often involved in complex multivariate gene selection approach, which has been proven not to be more effective than simple univariate gene selection approach in most cases [7, 18]. In this study, we proposed two new two-gene classification algorithms based on univariate gene selection strategy. We simply selected two genes with the largest absolute t-statistic values, and then constructed classification rules based on their optimal cut-points of expression levels. We detected the optimal cut-point according to the information entropy principle [19].
We compared the performance of the two-gene classification models to that of the TSP [8] and the greedy pairs (GP) based classification models [17]. We also compared the performance of our classifiers with the popularly-used standard models including Diagonal Linear Discriminant Analysis (DLDA), k-Nearest Neighbor (k-NN), Support Vector Machines (SVM) and Random Forest (RF). The materials studied involved eleven publicly available gene expression datasets (http://linus.nci.nih.gov/~brb/DataArchive_New.html) [20].
2 Methods
2.1 Construction of Two-gene Classifiers
Within each training set, we calculated the value of the t-statistic (t-score) for each gene, and then selected the two genes with the highest absolute values of t-score to build classification rules. Here we obtained the t-score based on the Welch’s t-test which supposes two groups of samples have possibly unequal variances.
We built the classification rules based on the optimal cut-points for the expression levels of the genes selected. We found the optimal cut-point by using the entropy-based discretization method [19]. In [21], we have given the description of the method for detection of the optimal cut-point. Here we simply repeated the essential procedure.
To obtain the optimal cut-point for gene g, we first sorted the training sample set S as s1, s2, …, sn, based on the expression levels of g, and then constructed the candidate cut-point set P which was composed of the mean values of E(g, sk) and E(g, sk+1) provided that sk and sk+1 were labeled with two different classes. Here E(g, si) denotes the expression level of gene g in the sample si. Each element t of P separated S into two equivalence classes S1(t, g) and S2(t, g), where S1(t, g)={s∈S | E(g, s) ≤ t} and S2(t, g)={s∈S | E(g, s) > t}. Let C1 denote the subset of samples whose class label is c1, and C2 the subset of samples whose class label is c2. Define the four sets: P11, P12, P21 and P22, where P11=S1(t, g)∩C1, P12=S1(t, g)∩C2, P21=S2(t, g)∩C1, and P22=S2(t, g)∩C2. We calculated the class information entropy of the partition induced by t, denoted E(g, t, S), as follows:
We selected the t which minimized E(g, t, S) as the optimal cut-point T(g) for g. If the candidate cut-point set P was empty (very rare), we took the mean expression level of g in all training samples as the optimal cut-point.
Once we obtained the optimal cut-point T(g) for the gene g, we built the single-gene classification rule based on g. Let Q11(g)=S1(T(g), g)∩C1, Q12(g)=S1(T(g), g)∩C2, Q21(g)=S2(T(g), g)∩C1, Q22(g)=S2(T(g), g)∩C2, and C(s) denote the class label assigned to the sample s. If |Q11(g)| + |Q22(g)| > |Q12(g)| + |Q21(g)|, the classification rule would be “E(g, s) ≤ T(g) => C(s)=c1; E(g, s) > T(g) => C(s)=c2”; otherwise, the classification rule would be “E(g, s) ≤ T(g) => C(s)=c2; E(g, s) > T(g) => C(s)=c1”.
We have used the above classification rule to construct single-gene classifiers by which we achieved ideal classification effect in most cases [21]. However, the single-gene classifiers’ performance would degrade if one noise gene was selected. The present two-gene classifiers were expected to attain more stable performance through combination of the classification rules induced by two genes. Here we constructed two types of two-gene classifiers termed as TGC-1 and TGC-2, respectively.
Suppose we selected another gene h with the second largest absolute t-score, apart from the gene g which had the largest absolute t-score. We denoted max(x, y) as the larger one between x and y. We constructed TGC-1’s classification rule as follows: if max(|Q11(g)|+|Q22(g)|, |Q12(g)|+|Q21(g)|) ≥ max(|Q11(h)|+|Q22(h)|, |Q12(h)|+|Q21(h)|), then the classification rule is the single-gene classification rule based on g; otherwise, the classification rule is the single-gene classification rule based on h.
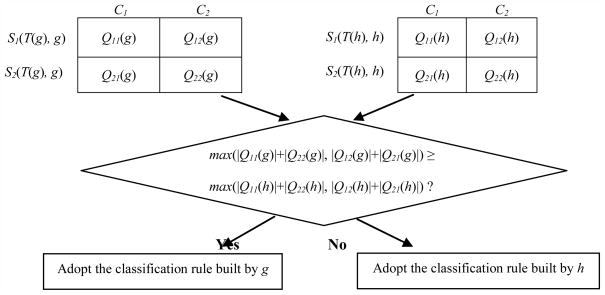
Here max(|Q11(g)|+|Q22(g)|, |Q12(g)|+|Q21(g)|) and max(|Q11(h)|+|Q22(h)|, |Q12(h)|+|Q21(h)|) indicate the number of samples correctly classified with gene g and h, respectively. Therefore, TGC-1 utilized the classification rule constructed merely based on one of the two selected genes which led to the optimal classification result (Fig. 1).
Fig. 1.
Construction of TGC-1’s classification rule.
TGC-1’s classification rule is built based on a single gene’s classification rule by comparison of the number of samples correctly classified with gene g and h.
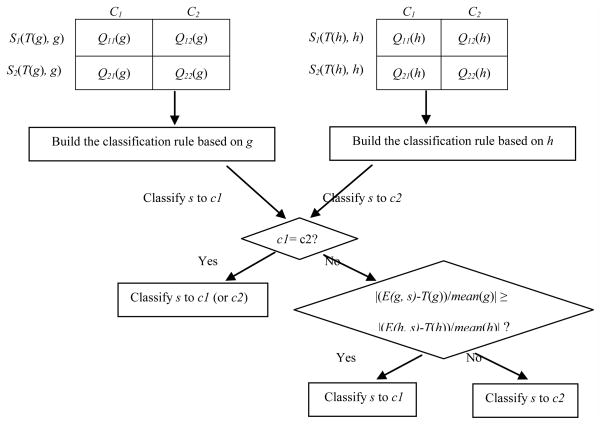
In contrast, we constructed TGC-2’s classification rule by taking into account the classification rules based on both genes selected simultaneously. As for a single gene x, we will encounter two cases: |Q11(x)| + |Q22(x)| > |Q12(x)| + |Q21(x)| and |Q11(x)| + |Q22(x)| ≤ |Q12(x)| + |Q21(x)|, we will have four different combinations for two genes. On the other hand, relative to the optimal cut-point, the expression level of gene x in a sample s can be divided into two cases: E(x, s) ≤ T(x) and E(x, s) > T(x). Thus, the expression levels of two genes in the same sample s will have four different possibilities. Suppose we classify s into class c1 and c2 by the classification rules based on gene x and y, respectively. If c1 is identical to c2, we will certainly classify s into class c1 (or c2); otherwise, we need to consider additional factors to determine the class label of s. One significant factor is the distance between the expression level of one gene and its optimal cut-point. If the distance regarding gene x is greater than that regarding gene y, we think that x has higher weight than y in determining the class attribute of s, and therefore adopt its classification rule to classify s. Because different genes possibly have very different average expression levels across samples, we normalized the distance via dividing it by the average expression level of each gene across all training samples. Fig. 2 illuminates the basic procedure of TGC-2.
Fig. 2.
Construction of TGC-2’s classification rule.
TGC-2’s classification rule is built by the weighted consideration of two single genes’ classification rules.
In detail, we constructed TGC-2’s classification rule as follows:
-
if |Q11(g)| + |Q22(g)| > |Q12(g)| + |Q21(g)| and |Q11(h)| + |Q22(h)| > |Q12(h)| + |Q21(h)|, then
E(g, s) ≤ T(g) and E(h, s) ≤ T(h) => C(s)=c1;
E(g, s) > T(g) and E(h, s) > T(h) => C(s)=c2;
-
if E(g, s) > T(g) and E(h, s) ≤ T(h), then
(E(g, s) − T(g))/|mean(g)| < (T(h) − E(h, s))/|mean(h)| => C(s)=c1;
(E(g, s) − T(g))/|mean(g)| ≥ (T(h) − E(h, s))/|mean(h)| => C(s)=c2;
-
if E(g, s) ≤ T(g) and E(h, s) > T(h), then
(T(g) − E(g, s))/|mean(g)| ≥ (E(h, s) − T(h))/|mean(h)| => C(s)=c1;
(T(g) − E(g, s))/|mean(g)| < (E(h, s) − T(h))/|mean(h)| => C(s)=c2;
-
if |Q11(g)| + |Q22(g)| > |Q12(g)| + |Q21(g)| and |Q11(h)| + |Q22(h)| ≤ |Q12(h)| + |Q21(h)|, then
E(g, s) ≤ T(g) and E(h, s) > T(h) => C(s)=c1;
E(g, s) > T(g) and E(h, s) ≤ T(h) => C(s)=c2;
-
if E(g, s) > T(g) and E(h, s) > T(h), then
(E(g, s) − T(g))/|mean(g)| < (E(h, s) − T(h) )/|mean(h)| => C(s)=c1;
(E(g, s) − T(g))/|mean(g)| ≥ (E(h, s) − T(h) )/|mean(h)| => C(s)=c2;
-
if E(g, s) ≤ T(g) and E(h, s) ≤ T(h), then
(T(g) − E(g, s))/|mean(g)| ≥ (T(h) − E(h, s))/|mean(h)| => C(s)=c1;
(T(g) − E(g, s))/|mean(g)| < (T(h) − E(h, s))/|mean(h)| => C(s)=c2;
-
if |Q11(g)| + |Q22(g)| ≤ |Q12(g)| + |Q21(g)| and |Q11(h)| + |Q22(h)| > |Q12(h)| + |Q21(h)|, then
E(g, s) > T(g) and E(h, s) ≤ T(h) => C(s)=c1;
E(g, s) ≤ T(g) and E(h, s) > T(h) => C(s)=c2;
-
if E(g, s) > T(g) and E(h, s) > T(h), then
(E(g, s) − T(g))/|mean(g)| ≥ (E(h, s) − T(h))/|mean(h)| => C(s)=c1;
(E(g, s) − T(g))/|mean(g)| < (E(h, s) − T(h))/|mean(h)| => C(s)=c2;
-
if E(g, s) ≤ T(g) and E(h, s) ≤ T(h), then
(T(g) − E(g, s))/|mean(g)| < (T(h) − E(h, s))/|mean(h)| => C(s)=c1;
(T(g) − E(g, s))/|mean(g)| ≥ (T(h) − E(h, s))/|mean(h)| => C(s)=c2;
-
if |Q11(g)| + |Q22(g)| ≤ |Q12(g)| + |Q21(g)| and |Q11(h)| + |Q22(h)| ≤ |Q12(h)| + |Q21(h)|, then
E(g, s) > T(g) and E(h, s) > T(h) => C(s)=c1;
E(g, s) ≤ T(g) and E(h, s) ≤ T(h) => C(s)=c2;
-
if E(g, s) > T(g) and E(h, s) ≤ T(h), then
(E(g, s) − T(g))/|mean(g)| ≥ (T(h) − E(h, s))/|mean(h)| => C(s)=c1;
(E(g, s) − T(g))/|mean(g)| < (T(h) − E(h, s))/|mean(h)| => C(s)=c2;
-
if E(g, s) ≤ T(g) and E(h, s) > T(h), then
(T(g) − E(g, s))/|mean(g)| < (E(h, s) − T(h))/|mean(h)| => C(s)=c1;
(T(g) − E(g, s))/|mean(g)| ≥ (E(h, s) − T(h))/|mean(h)| => C(s)=c2;
Here mean(i) indicates the average expression levels of gene i across all training samples.
2.2 Evaluation of Classifier Performance
We evaluated classifier performance by leave-one-out cross validation (LOOCV). In each leave-one-out training set, we selected two genes based on which the classification rule was constructed to classify the omitted sample. We used TGC-1 and TGC-2 to classify each dataset, respectively, and thus we obtained two sets of classification accuracy results.
We compared the performance of our models to that of the gene pairs based classification models TSP and GP, as well as four standard classifiers: DLDA, k-NN, SVM and RF. For the TSP classifier, the number of gene pairs selected was set as one. For the GP model, we first selected one pair of genes based on the greedy-pairs approach proposed in [17], and then used DLDA, k-NN and SVM algorithms to perform classification with the two genes selected, respectively. For k-NN, we set the parameter k as 3. The SVM was based on the linear inner product kernel function (cost=1). For RF, we set the number of trees and genes randomly sampled as candidates at each split as 100 and the squared root of the total number of genes, respectively. For the four standard classifiers, the genes significantly different between the classes at 0.001 significance level were used for class prediction. We carried out all the compared classification algorithms in BRB-ArrayTools, an integrated package for the visualization and statistical analysis of DNA microarray gene expression data (http://linus.nci.nih.gov/BRB-ArrayTools.html) [22].
2.3 Materials
We selected eleven gene expression datasets to evaluate classifier performance. These datasets have different scale of sample size and gene number. For the Melanoma, Breast Cancer 2, Gastric Tumor, Lung Cancer 2 and Myeloma datasets, we performed pre-filtering of gene due to computational cost. Thus, the gene numbers presented in the five datasets are post-filtering gene numbers, while the gene numbers shown in the other datasets are the original gene numbers published (Table 1).
Table 1.
Summary of the eleven gene expression datasets
| Dataset | # Genes | Class | # Samples* |
|---|---|---|---|
| Melanoma [23] | 18256 | malignant/nonmalignant | 70(45/25) |
| Breast Cancer 1 [24] | 7650 | relapse/no-relapse | 99 (45/54) |
| Brain Cancer [25] | 7129 | classic/desmoplastic | 60 (46/14) |
| Breast Cancer 2 [15] | 17985 | disease-free/cancer recurred | 60 (32/28) |
| Gastric Tumor [26] | 7195 | normal/tumor | 132 (29/103) |
| Lung Cancer 1 [27] | 12600 | squamous cell lung carcinoma/pulmonary carcinoid | 41 (21/20) |
| Lung Cancer 2 [28] | 6321 | mesothelioma/adenocarcinoma | 181 (31/150) |
| Lymphoma [29] | 7129 | cured/fatal | 58 (32/26) |
| Myeloma [30] | 6451 | without bone lytic lesion/with bone lytic lesion | 173 (36/137) |
| Pancreatic Cancer [31] | 22283 | Normal/pancreatic ductal carcinoma | 49 (25/24) |
| Prostate Cancer [32] | 12600 | normal/tumor | 102 (50/52) |
Note: The sample size of each class is given in parenthesis.
3 Results
3.1 Comparison with the TSP classifier
Table 2 lists the LOOCV results for TSP, TGC-1 and TGC-2. From Table 2, we can see that in the Melanoma, Brain Cancer, Lung Cancer 1, Lung Cancer 2 and Lymphoma datasets, the classification accuracy obtained by our methods matches that obtained by TSP. In the Breast Cancer 1, Myeloma and Pancreatic Cancer datasets, TSP shows higher accuracy than our methods, while in the Breast Cancer 2, Gastric Tumor and Prostate Cancer datasets, our methods exhibit higher accuracy than TSP. Generally speaking, for the datasets examined, our two-gene classifiers show comparable performance with TSP.
Table 2.
Comparison of classification accuracy (%) with the TSP classifier
| Method | TSP | TGC-1 | TGC-2 |
|---|---|---|---|
| Dataset | |||
| Melanoma | 99 | 97 | 96 |
|
| |||
| Breast Cancer 1 | 75 | 64 | 64 |
|
| |||
| Brain Cancer | 77 | 77 | 75 |
|
| |||
| Breast Cancer 2 | 70 | 82 | 78 |
|
| |||
| Gastric Tumor | 66 | 89 | 88 |
|
| |||
| Lung Cancer 1 | 95 | 98 | 100 |
|
| |||
| Lung Cancer 2 | 94 | 93 | 93 |
|
| |||
| Lymphoma | 57 | 59 | 60 |
|
| |||
| Myeloma | 79 | 68 | 54 |
|
| |||
| Pancreatic Cancer | 90 | 71 | 73 |
|
| |||
| Prostate Cancer | 81 | 89 | 90 |
3.2 Comparison with the GP model
Table 3 compares the classification accuracy by our models to that by DLDA, k-NN, and SVM with the GP gene selection approach. Here we term the classification models based on the GP gene selection approach the GP model regardless of what classification rule is used.
Table 3.
Comparison of classification accuracy (%) with the GP model
| Method | TGC-1 | TGC-2 | GP | ||
|---|---|---|---|---|---|
| Dataset | DLDA | k-NN | SVM | ||
| Melanoma | 97 | 96 | 86 | 90 | 84 |
|
| |||||
| Breast Cancer 1 | 64 | 64 | 74 | 60 | 68 |
|
| |||||
| Brain Cancer | 77 | 75 | 67 | 63 | 67 |
|
| |||||
| Breast Cancer 2 | 82 | 78 | 62 | 57 | 60 |
|
| |||||
| Gastric Tumor | 89 | 88 | 80 | 77 | 81 |
|
| |||||
| Lung Cancer 1 | 98 | 100 | 98 | 95 | 95 |
|
| |||||
| Lung Cancer 2 | 93 | 93 | 86 | 89 | 91 |
|
| |||||
| Lymphoma | 59 | 60 | 69 | 64 | 67 |
|
| |||||
| Myeloma | 68 | 54 | 60 | 69 | 78 |
|
| |||||
| Pancreatic Cancer | 71 | 73 | 78 | 76 | 73 |
|
| |||||
| Prostate Cancer | 89 | 90 | 87 | 82 | 85 |
From Table 3, we can see that in the Melanoma, Brain Cancer, Breast Cancer 2 and Gastric Tumor datasets, the classification accuracy obtained by our methods are higher than that obtained by GP. In Breast Cancer 1, Lung Cancer 1, Lung Cancer 2, Pancreatic Cancer and Prostate Cancer datasets, our methods and GP achieved close accuracy. In the Lymphoma and Myeloma datasets, our methods exhibit a bit poorer accuracy than GP. Overall, our two-gene classification models surpassed GP in prediction performance for the datasets examined.
3.3 Comparison with the standard classifiers
Table 4 compares the classification accuracy between the two-gene classifiers and the standard classifiers. From Table 4, we can see that in the Breast Cancer 1, Brain Cancer, Breast Cancer 2 and Pancreatic Cancer datasets, our methods consistently achieved higher accuracy than all the standard classifiers. In Melanoma, Gastric Tumor, Lung Cancer 1, Lung Cancer 2, Lymphoma and Prostate Cancer datasets, our methods show comparable performance with the standard classifiers. Only in the Myeloma dataset, our methods exhibit poorer accuracy than the standard classifiers. All together, these results indicate that our two-gene classifiers have better performance than the standard classifiers for the datasets examined, lending a support to the notion that simple models outstrip complicated ones in molecular prediction of cancer based on gene expression profiling.
Table 4.
Comparison of classification accuracy (%) with the standard classifiers
| Method | TGC-1 | TGC-2 | DLDA | k-NN | SVM |
|---|---|---|---|---|---|
| Dataset | |||||
| Melanoma | 97 | 96 | 97 | 97 | 97 |
|
| |||||
| Breast Cancer 1 | 64 | 64 | 53 | 52 | 43 |
|
| |||||
| Brain Cancer | 77 | 75 | 73 | 60 | 70 |
|
| |||||
| Breast Cancer 2 | 82 | 78 | 70 | 72 | 70 |
|
| |||||
| Gastric Tumor | 89 | 88 | 96 | 98 | 92 |
|
| |||||
| Lung Cancer 1 | 98 | 100 | 98 | 98 | 98 |
|
| |||||
| Lung Cancer 2 | 93 | 93 | 99 | 99 | 99 |
|
| |||||
| Lymphoma | 59 | 60 | 52 | 59 | 57 |
|
| |||||
| Myeloma | 68 | 54 | 80 | 76 | 79 |
|
| |||||
| Pancreatic Cancer | 71 | 73 | 61 | 65 | 55 |
|
| |||||
| Prostate Cancer | 89 | 90 | 93 | 93 | 93 |
Indeed, the average number of genes used for building the standard classifiers ranged from tens to thousands, whereas their performance was not superior to the two-gene classifiers. One sensible explanation is that for the gene expression data involving high-dimensional attributes (p) and low-dimensional instances (n), if too many attributes are selected for construction of classifiers, over-fitting is likely to occur.
4 Discussion and Conclusions
For the p>n problem such as microarray classification, good performance can often be achieved with a small number of genes, even a pair of genes. Indeed, in some cases, accurate classification can be achieved with one single gene [3, 21]. Previously, we developed the single-gene models which were frequently of commensurate accuracy as more complex classifiers, whereas in some cases, the single-gene models performed poorly because of the selection of noise genes [21]. The present two-gene classification models to a large extent overcame the unstability drawback of the single-gene models because it is highly improbable to select two noise genes simultaneously.
We can’t evaluate the complexity of a classification model simply based on the number of genes in the model. Complexity also depends on gene selection criteria and classification rules employed. Simple models typically involve a simple feature selection scheme and simple classification rule. In contrast, complex models often involve sophisticated feature selection procedures and/or complicated classification rules [21]. Although TSP, GP and our models were all involved in gene pairs, TSP and GP were actually more complex than our models. The TSP algorithm performed gene pair selection by searching for all gene pair combinations that is computationally expensive. The GP algorithm evaluated a subset of all gene pair combinations by first ranking all genes based on individual t-score, which was less computationally expensive than the TSP algorithm but more computationally expensive than our algorithm. Indeed, neither of TSP and GP was a genuine two-gene classification algorithm in that they actually embraced multiple gene pairs in construction of classification rules.
Our algorithm selected two genes on the basis of their individual t-score. Therefore, gene interaction information was not considered by our strategy. In fact, the detection of interaction between genes among thousands or tens of thousands candidates is very time-consuming. That was why the TSP and GP algorithms had lower time efficiency than our algorithm. In fact, gene interaction information might not exert a significant influence on classification performance [7, 18].
The classification accuracies obtained by TGC-1 and TGC-2 were very close to each other except for in the Myeloma dataset. Both classifiers utilized the identical two genes but different classification rules. Actually, the classification rule used by TGC-1 was the single-gene classification rule. Its excellent performance manifested that the single-gene classification rule was a reasonable choice if the single gene selected was not a noise gene. In contrast, TGC-2 indeed used the two gene selected to construct the classification rule which was more complex than that of TGC-1. Thus, the performance of TGC-2 relied on both genes while the performance of TGC-1 depended upon only one of both genes. That means TGC-1 is a more robust classifier than TGC-2 in that any one noise gene in the gene pair selected will comprise the performance of TGC-2 but not affect that of TGC-1 if the other gene is informative. The great gap between the classification accuracies produced by TGC-1 and TGC-2 in the Myeloma dataset may exemplify this point.
Here we selected two genes with the largest absolute values of t-score. An alternative approach is to select two genes with one gene having the largest positive value of t-score and another gene having the smallest negative value of t-score. This approach seems to be a sensible choice in that based on it, we may select one gene with much higher expression levels in one class and another gene with much higher expression levels in another class. In fact, many two-gene classifiers select gene pairs based on similar criteria including the TSP classifier, and our method has 50% chance of meeting this selection. Table 5 compares the performance between TGC-1, TGC-2 and the two-gene classifier constructed based on the alternative gene selection approach and the same classification rule as that used by TGC-2 (TGC-Mm). Apparently, in most cases, the alternative two-gene classifier has comparable performance with TGC-1 and TGC-2, whereas in a few cases, it shows poorer performance than TGC-1 and TGC-2 such as in the Lymphoma, Myeloma and Pancreatic Cancer datasets. One possible explanation for the performance gap in these datasets is that there may are much more genes having obviously higher expression levels in one class (class 1) than in another class (class 2) in these datasets so that the selection of two genes with higher expression levels in class 1 is more reasonable than the selection of two genes with higher expression levels in class 1 and class 2, respectively.
Table 5.
Comparison of classification accuracy (%) with the alternative two-gene classifier
| Method | TGC-Mm | TGC-1 | TGC-2 |
|---|---|---|---|
| Dataset | |||
| Melanoma | 97 | 97 | 96 |
|
| |||
| Breast Cancer 1 | 64 | 64 | 64 |
|
| |||
| Brain Cancer | 75 | 77 | 75 |
|
| |||
| Breast Cancer 2 | 78 | 82 | 78 |
|
| |||
| Gastric Tumor | 89 | 89 | 88 |
|
| |||
| Lung Cancer 1 | 98 | 98 | 100 |
|
| |||
| Lung Cancer 2 | 95 | 93 | 93 |
|
| |||
| Lymphoma | 52 | 59 | 60 |
|
| |||
| Myeloma | 47 | 68 | 54 |
|
| |||
| Pancreatic Cancer | 63 | 71 | 73 |
|
| |||
| Prostate Cancer | 88 | 89 | 90 |
In this study, we developed genuine two-gene classification models. Through experimental test on several gene expression datasets, we found that although our two-gene classification algorithms were simpler than existing two-gene classification algorithms like TSP and GP, our classifiers’ performance was comparable to or better than that of TSP and GP. Moreover, our classifiers exhibited better performance than the standard classifiers DLDA, k-NN, SVM and RF, even though they used much more genes for classification. This study strengthens the consensus that simple classifiers have essential advantages over complicated ones, and therefore should be preferable for cancerous prediction based on gene expression profiling.
Highlights.
We proposed two new simple two-gene classification models for cancer prediction based on gene expression profiles.
Our models used simple univariate gene selection strategy.
Our models constructed simple classification rules based on information entropy principle.
The performance of our models was comparable to or better than that of some existing two-gene classification models or multi-gene standard methods.
Simple models have substantial advantages over complicated ones in molecular predication of cancer.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Simon R. Supervised analysis when the number of candidate feature (p) greatly exceeds the number of cases (n) ACM SIGKDD Explorations Newsletter. 2003;5:31–36. [Google Scholar]
- 2.Simon R, Radmacher MD, Dobbin K, McShane LM. Pitfalls in the use of DNA microarray data for diagnostic and prognostic classification. J Natl Cancer Inst. 2003;95:14–18. doi: 10.1093/jnci/95.1.14. [DOI] [PubMed] [Google Scholar]
- 3.Wang X, Gotoh O. Accurate molecular classification of cancer using simple rules. BMC Med Genomics. 2009;2:64. doi: 10.1186/1755-8794-2-64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baker SG. Simple and flexible classification of gene expression microarrays via Swirls and Ripples. BMC Bioinformatics. 2010;11:452. doi: 10.1186/1471-2105-11-452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li J, Liu H, Downing JR, Yeoh AE, Wong L. Simple rules underlying gene expression profiles of more than six subtypes of acute lymphoblastic leukemia (ALL) patients. Bioinformatics. 2003;19:71–78. doi: 10.1093/bioinformatics/19.1.71. [DOI] [PubMed] [Google Scholar]
- 6.Wessels LFA, Reinders MJT, Hart AAM, Veenman CJ, Dai H, He YD, van’t Veer LJ. A protocol for building and evaluating predictors of disease state based on microarray data. Bioinformatics (Oxford, England) 2005;21:3755–3762. doi: 10.1093/bioinformatics/bti429. [DOI] [PubMed] [Google Scholar]
- 7.Dudoit S, Fridlyand J. Classification in microarray experiments. In: Speed T, editor. Statistical Analysis of Gene Expression Microarray Data. Chapman & Hall/CRC; 2003. pp. 93–158. [Google Scholar]
- 8.Geman D, d’Avignon C, Naiman DQ, Winslow RL. Classifying gene expression profiles from pairwise mRNA comparisons. Stat Appl Genet Mol Biol. 2004;3:Article 19. doi: 10.2202/1544-6115.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tan AC, Naiman DQ, Xu L, Winslow RL, Geman D. Simple decision rules for classifying human cancers from gene expression profiles. Bioinformatics. 2005;21:3896–3904. doi: 10.1093/bioinformatics/bti631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Edelman LB, Toia G, Geman D, Zhang W, Price ND. Two-transcript gene expression classifiers in the diagnosis and prognosis of human diseases. BMC Genomics. 2009;10:583. doi: 10.1186/1471-2164-10-583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Xu L, Tan AC, Naiman DQ, Geman D, Winslow RL. Robust prostate cancer marker genes emerge from direct integration of inter-study microarray data. Bioinformatics. 2005;21:3905–3911. doi: 10.1093/bioinformatics/bti647. [DOI] [PubMed] [Google Scholar]
- 12.Zhao H, Logothetis CJ, Gorlov IP. Usefulness of the top-scoring pairs of genes for prediction of prostate cancer progression. Prostate Cancer Prostatic Dis. 2010;13:252–259. doi: 10.1038/pcan.2010.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Patnaik SK, Kannisto E, Knudsen S, Yendamuri S. Evaluation of microRNA expression profiles that may predict recurrence of localized stage I non-small cell lung cancer after surgical resection. Cancer Res. 2010;70:36–45. doi: 10.1158/0008-5472.CAN-09-3153. [DOI] [PubMed] [Google Scholar]
- 14.Raponi M, Lancet JE, Fan H, Dossey L, Lee G, Gojo I, Feldman EJ, Gotlib J, Morris LE, Greenberg PL, Wright JJ, Harousseau JL, Lowenberg B, Stone RM, De Porre P, Wang Y, Karp JE. A 2-gene classifier for predicting response to the farnesyltransferase inhibitor tipifarnib in acute myeloid leukemia. Blood. 2008;111:2589–2596. doi: 10.1182/blood-2007-09-112730. [DOI] [PubMed] [Google Scholar]
- 15.Ma XJ, Wang Z, Ryan PD, Isakoff SJ, Barmettler A, Fuller A, Muir B, Mohapatra G, Salunga R, Tuggle JT, Tran Y, Tran D, Tassin A, Amon P, Wang W, Wang W, Enright E, Stecker K, Estepa-Sabal E, Smith B, Younger J, Balis U, Michaelson J, Bhan A, Habin K, Baer TM, Brugge J, Haber DA, Erlander MG, Sgroi DC. A two-gene expression ratio predicts clinical outcome in breast cancer patients treated with tamoxifen. Cancer cell. 2004;5:607–616. doi: 10.1016/j.ccr.2004.05.015. [DOI] [PubMed] [Google Scholar]
- 16.Price ND, Trent J, El-Naggar AK, Cogdell D, Taylor E, Hunt KK, Pollock RE, Hood L, Shmulevich I, Zhang W. Highly accurate two-gene classifier for differentiating gastrointestinal stromal tumors and leiomyosarcomas. Proc Natl Acad Sci U S A. 2007;104:3414–3419. doi: 10.1073/pnas.0611373104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bo T, Jonassen I. New feature subset selection procedures for classification of expression profiles. Genome biology. 2002;3:RESEARCH0017. doi: 10.1186/gb-2002-3-4-research0017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lai C, Reinders MJT, van’t Veer LJ, Wessels LFA. A comparison of univariate and multivariate gene selection techniques for classification of cancer datasets. BMC bioinformatics. 2006;7:235. doi: 10.1186/1471-2105-7-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fayyad UM, Irani KB. Multi-interval discretization of continuous-valued attributes for classification learning. Proceedings of the 13th International Joint Conference of Artificial Intelligence; Chambéry, France: Morgan Kaufmann; 1993. pp. 1022–1027. [Google Scholar]
- 20.Zhao Y, Simon R. BRB-ArrayTools Data Archive for human cancer gene expression: a unique and efficient data sharing resource. Cancer Inform. 2008;6:9–15. doi: 10.4137/cin.s448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang X, Simon R. Microarray-based Cancer Prediction Using Single Genes. BMC Bioinformatics. 2011;12:391. doi: 10.1186/1471-2105-12-391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Simon R, Lam A, Li MC, Ngan M, Menenzes S, Zhao Y. Analysis of Gene Expression Data Using BRB-Array Tools. Cancer Informatics. 2007;3:11–17. [PMC free article] [PubMed] [Google Scholar]
- 23.Talantov D, Mazumder A, Yu JX, Briggs T, Jiang Y, Backus J, Atkins D, Wang Y. Novel genes associated with malignant melanoma but not benign melanocytic lesions. Clinical cancer research: an official journal of the American Association for Cancer Research. 2005;11:7234–7242. doi: 10.1158/1078-0432.CCR-05-0683. [DOI] [PubMed] [Google Scholar]
- 24.Sotiriou C, Neo SY, McShane LM, Korn EL, Long PM, Jazaeri A, Martiat P, Fox SB, Harris AL, Liu ET. Breast cancer classification and prognosis based on gene expression profiles from a population-based study. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:10393–10398. doi: 10.1073/pnas.1732912100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pomeroy SL, Tamayo P, Gaasenbeek M, Sturla LM, Angelo M, McLaughlin ME, Kim JYH, Goumnerova LC, Black PM, Lau C, Allen JC, Zagzag D, Olson JM, Curran T, Wetmore C, Biegel JA, Poggio T, Mukherjee S, Rifkin R, Califano A, Stolovitzky G, Louis DN, Mesirov JP, Lander ES, Golub TR. Prediction of central nervous system embryonal tumour outcome based on gene expression. Nature. 2002;415:436–442. doi: 10.1038/415436a. [DOI] [PubMed] [Google Scholar]
- 26.Chen X, Leung SY, Yuen ST, Chu KM, Ji J, Li R, Chan ASY, Law S, Troyanskaya OG, Wong J, So S, Botstein D, Brown PO. Variation in gene expression patterns in human gastric cancers. Mol Biol Cell. 2003;14:3208–3215. doi: 10.1091/mbc.E02-12-0833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bhattacharjee A, Richards WG, Staunton J, Li C, Monti S, Vasa P, Ladd C, Beheshti J, Bueno R, Gillette M, Loda M, Weber G, Mark EJ, Lander ES, Wong W, Johnson BE, Golub TR, Sugarbaker DJ, Meyerson M. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:13790–13795. doi: 10.1073/pnas.191502998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gordon GJ, Jensen RV, Hsiao LL, Gullans SR, Blumenstock JE, Ramaswamy S, Richards WG, Sugarbaker DJ, Bueno R. Translation of microarray data into clinically relevant cancer diagnostic tests using gene expression ratios in lung cancer and mesothelioma. Cancer Res. 2002;62:4963–4967. [PubMed] [Google Scholar]
- 29.Shipp MA, Ross KN, Tamayo P, Weng AP, Kutok JL, Aguiar RCT, Gaasenbeek M, Angelo M, Reich M, Pinkus GS, Ray TS, Koval MA, Last KW, Norton A, Lister TA, Mesirov J, Neuberg DS, Lander ES, Aster JC, Golub TR. Diffuse large B-cell lymphoma outcome prediction by gene-expression profiling and supervised machine learning. Nature medicine. 2002;8:68–74. doi: 10.1038/nm0102-68. [DOI] [PubMed] [Google Scholar]
- 30.Tian E, Zhan F, Walker R, Rasmussen E, Ma Y, Barlogie B, Shaughnessy JD. The role of the Wnt-signaling antagonist DKK1 in the development of osteolytic lesions in multiple myeloma. N Engl J Med. 2003;349:2483–2494. doi: 10.1056/NEJMoa030847. [DOI] [PubMed] [Google Scholar]
- 31.Ishikawa M, Yoshida K, Yamashita Y, Ota J, Takada S, Kisanuki H, Koinuma K, Choi YL, Kaneda R, Iwao T, Tamada K, Sugano K, Mano H. Experimental trial for diagnosis of pancreatic ductal carcinoma based on gene expression profiles of pancreatic ductal cells. Cancer science. 2005;96:387–393. doi: 10.1111/j.1349-7006.2005.00064.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Singh D, Febbo PG, Ross K, Jackson DG, Manola J, Ladd C, Tamayo P, Renshaw AA, D’Amico AV, Richie JP, Lander ES, Loda M, Kantoff PW, Golub TR, Sellers WR. Gene expression correlates of clinical prostate cancer behavior. Cancer cell. 2002;1:203–209. doi: 10.1016/s1535-6108(02)00030-2. [DOI] [PubMed] [Google Scholar]