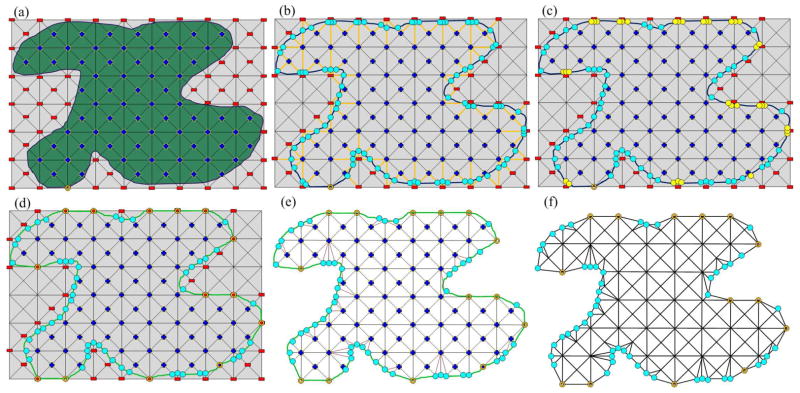
Figure 2.
A two dimensional illustration of our tetrahedral generation algorithm. Note that the octree subdivision is adaptive in our algorithm. However, we do not show the adaptivity here for simplicity. (a) Computing the signs for each BCC grid; (b) Calculating the cutting points; (c) Detecting the “too close” cutting points; (d) Snapping the “too close” cutting points to the corresponding BCC lattice grids; (e) Decomposing the boundary polyhedra into tetrahedra; (f) Obtaining the final tetrahedral mesh.