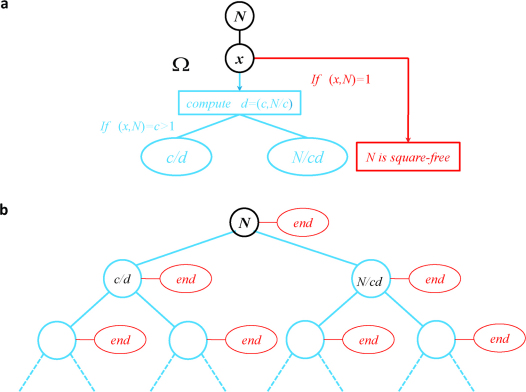
Figure 2. Schematic flow chart of the recursive quantum algorithm for computing the squrare-free part of an arbitrary odd integer N.

(a) Possible outcomes of applying the algorithm Ω on an arbitrary odd integer N: either return a factor c or else ensure that N is a square-free number with the square-free part r = N. If a factor c > 1 is returned, and N is tested to be not square-free, then the problem is converted to two smaller sub-problems for c/d and N/cd where d is the greatest common divisor of c and N/c.This serves as the subroutine of the recursive quantum algorithm. (b) Recursive algorithm for a general N. Different colors are used to designate two different outcomes after applying the subroutine Ω. The red color denotes that number is square-free, then this branch terminates. The blue color denotes the other outcome; in this case, the algorithm proceeds to the next step of recursion. The Ω operation needs to be performed at most log N times to solve this problem.