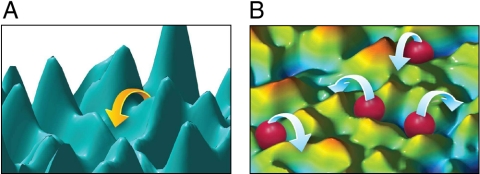
Fig. 4.

Pictorial demonstration of different physical mechanisms leading to a broad distribution of relaxation rates. (A) The energy landscape of various complex systems, including glasses, contains many minima. The energetic barriers separating them are smoothly distributed over a certain range. In order for the system to relax its energy, it must cross these barriers by thermal activation or by quantum mechanical tunneling: Both are exponential in the barrier, which lead to a rate distribution described by P(λ) ∼ 1/λ, as we discuss in detail. (B) Many particle transitions in an electron glass are an example of a multiplicative process: In many electronic configurations, moving any single electron in the system to one of the vacant sites will result in higher energy, and therefore these processes will not occur at low enough temperatures. However, changing the position of a larger number of electrons can result in a lower energy. The rates of this process can be approximately written as a product of the rates of the single particle processes involved, leading to a rate distribution described by a log-normal distribution.