Some lessons about models from Michaelis and Menten

Abstract

Michaelis and Menten's classic 1913 paper on enzyme kinetics is used to draw some lessons about the relationship between mathematical models and biological reality.

These days, it is no longer so uncommon to find an experimental paper that includes a mathematical model. This may seem a surprising and perhaps even unwelcome intrusion into the qualitative world of molecular biology. In fact, quantitative methods and mathematical tools have always been used in biology, going back to Harvey's wonderful demonstration of the circulation of the blood. If this synergy is not widely appreciated, it is because our historical memories are woefully short. In consequence, there is little shared understanding about models.

I coteach, with one of my colleagues, Johan Paulsson, the introductory course in Harvard's graduate program in systems biology. The students come from an unnervingly broad spectrum of backgrounds in biology and the physical sciences, and one of the trickiest issues is how to get across what a model is and what one can, and cannot, expect from it. I find that it is easier to discuss this in the context of something that everyone needs to know. The famous Michaelis–Menten formula is a good choice, as it still provides insights for anyone wanting to understand how models really work (see Johnson and Goody, 2011, for a recent English translation of the German original, Michaelis and Menten, 1913).

There are several intersecting threads that appear in the discussion that follows, and I can only touch on a couple while leaving hints at others, which I hope to follow up at a later date.

In the early years of the 19th century, it was found experimentally that, if an enzyme E converts substrate S to product P, then the rate of change of concentration of the product, d[P]/dt, generally depends on the concentration of substrate, [S], through the now-familiar hyperbolic curve. The response is highly nonlinear. No matter how much the substrate concentration is increased, the rate never increases beyond a certain maximal amount; it saturates. This is what Michaelis and Menten found for invertase, the enzyme that splits sucrose into glucose and fructose and eponymously inverts the optical rotation, thereby providing the means to measure the enzyme rate with a polarimeter.

The likely explanation for enzyme saturation occurred to several people independently, including Adrian Brown in England and Victor Henri in France (Laidler, 1997): the enzyme was binding to the substrate to form some kind of enzyme–substrate complex. If the amount of enzyme was limited compared with that of the substrate, as is typically the case for in vitro studies, then the enzyme–substrate complex would act as a bottleneck. In the usual account in the textbooks, Michaelis and Menten substantiated this intuition by considering the reaction scheme

in which enzyme and substrate reversibly bind to form the enzyme–substrate complex ES before catalytically releasing enzyme and the product (as to why this last reaction is irreversible, see the later discussion). They deduced from this scheme, via a little algebra that has tortured generations of students, their now-familiar formula

and they showed that it gave a good fit to the experimental data. The mathematical formula provides a much richer understanding of enzyme behavior than informal intuition, as explained in the textbooks (e.g., Cornish-Bowden, 1995). This is the conventional account of what Michaelis and Menten achieved.

It is a good story as far as it goes, but it rather misses the point. There is an elephant in the room—the enzyme–substrate complex, ES. Michaels and Menten did not isolate this or characterize it in any way. They never got their hands on the underlying rate constants for binding and unbinding in scheme 1, which would have confirmed how the enzyme–substrate complex was formed. In their time, the enzyme–substrate complex was a hypothetical construct—a theory, one might even say a convenient fiction. The first person to confirm the existence of enzyme–substrate complexes was Britton Chance (Chance, 1943), who, no less than 30 years after Michaelis and Menten, developed the stopped-flow techniques needed to isolate intermediate complexes and measure binding and unbinding rates (Anderson, 2003). As Chance put it, “it is the purpose of this research … to show whether the Michaelis theory is an adequate explanation of enzyme mechanism.” Talking about Michaelis and Menten without mentioning Chance is like writing an opera without the fat lady.

This historical episode reveals an aspect of mathematics that is rarely brought out in discussions of modeling. What makes Michaelis and Menten's model so significant was not that it fits the experimental data, but that it provides evidence for something unseen. A theoretical entity explained the data in such a compelling way that biochemists adopted the theory for studying all enzymes. Michaelis and Menten used mathematics to show us how to think about enzymes.

The theory worked so well that biochemists used it without confirmation for thirty years. J. B. S. Haldane, better known as one of the founders of population genetics but also a student of Frederick Gowland Hopkins' great school of biochemistry at Cambridge, wrote in 1930, well before Chance's work, an entire book on enzyme–substrate theory (Haldane, 1965). The equivalent situation in physics would be if physicists started using positively charged electrons as soon as Dirac predicted their existence, instead of remaining skeptical until Anderson found the positron experimentally. This tells us something remarkable. Biology is more theoretical than physics. This is Michaelis and Menten's first lesson.

However contrary to popular prejudice this may seem, we really should not be so surprised. After all, biology is more difficult than physics; it needs all the help it can get. Indeed, the enzyme–substrate complex is only one of several theoretical entities for which mathematics provided a compelling justification for their introduction into biology long before their experimental identification.

If Michaelis and Menten's work was about the enzyme–substrate complex, then there is something rather odd about their formula. The enzyme–substrate complex is nowhere to be seen (out of sight, out of mind?). Somewhere in the algebra between the reactions in Eq. 1 and the formula in Eq. 2, the concentrations of the free enzyme E and the enzyme–substrate complex ES have been eliminated, leaving a formula involving just [S] and [P]. To accomplish this sleight of hand, Michaelis and Menten introduced into biology a neat trick widely used in physics. They assumed a separation of time scales in which E and ES rapidly reach a ready state, while S and P adjust to that steady state on a slower time scale (I gloss over the historical details; see Cornish-Bowden, 1995). In the typical in vitro situation, in which substrate is in substantial excess over enzyme, this time-scale separation seems intuitively reasonable. It is the starting point for the algebraic torture mentioned earlier and the key to the algebraic elimination.

Time-scale separation is very useful. It is one of the few conceptual tools that we have for eliminating internal complexity and deriving simplified descriptions of system behavior. It has been used in a wide variety of biological contexts, from enzyme kinetics to posttranslational modification (Thomson and Gunawardena, 2009), and we now understand how to do the eliminations for systems a lot more complex than enzymes (Gunawardena, unpublished results). It is another matter to identify the conditions under which the time-scale separation yields a good approximation to the original system (Schnell and Maini, 2003; Chen et al., 2010).

An experimentalist naturally wants to know what all this mathematical fandango actually tells us about reality. Which reality? Let us start with the in vitro reality of the biochemist and look more closely at what is going on inside that test tube. The first thing that stands out is that enzymes are reversible. If there is sufficient product, the enzyme will work in reverse, and the product will inhibit the forward reaction. Why, then, did Michaelis and Menten assume an irreversible catalytic step?

Well, they were very smart. They measured the rate of the reaction when it had just started, with almost no product present. Under such conditions, the reverse reaction is negligible. By assuming irreversibility in their reaction scheme, they greatly simplified their formula. Had they not done so, they would have had to derive the more complex formula that allows for product inhibition:

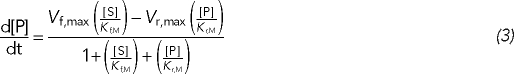(Few students survive the torture needed to calculate Eq. 3, but it is a standard exercise in biochemistry; see Cornish-Bowden, 1995.) Equation 3 reduces to Eq. 2 when [P] = 0. The four parameters—two each for the forward and reverse directions—must be estimated by fitting the data. Measuring initial rates allowed Michaelis and Menten to cut the complexity of their data analysis by half and to use a formula that was much easier to interpret than Eq. 3.

We usually think of modeling as helping experiment, but here careful choice of experimental setup helps the modeling. There is a good lesson in this, but there is an even better one lurking in the details. The conventional story about Michaelis and Menten emphasizes their formula, as I have done up to now. However, it was the experimental aspect of their paper that was its most compelling feature at the time. They were the first to get reproducible data on enzyme rates. It had to do with something that biochemists are now so familiar with that they barely mention it—pH. It was Michaelis who first understood the importance of pH in regulating enzyme activity. It was he who developed techniques for buffering reactions and introduced a generation of biologists to their importance in his widely influential book (Michaelis, 2010), which appeared in 1914, the year after his paper with Menten. An acetate buffer at optimal pH enabled Michaelis and Menten to get beautiful data on invertase.

The strange thing, however, is that there is no pH dependence in their model. Hydrogen ion concentration nowhere appears as a variable; the buffers are not mentioned, and none of the rates, or other parameters, is assumed to depend on pH. The model, in other words, is not at all a realistic description of what was actually going on in the test tube, nor is it a realistic description of a reversible enzyme. However, it is impeccably accurate at describing what was measured. We deduce something rather interesting from this. Models are not descriptions of reality; they are descriptions of our assumptions about reality. This is Michaelis and Menten's second lesson. It may come as a shock to some, but I cannot overemphasize its significance for appreciating how models and experiments relate to each other.

It is tempting to believe that models should be determined by the reality being studied. Models are then objective constructions, similar to those that engineers use. Because they are independent of the questions being asked, they have a predictive capacity, and this capacity should get better and better by including more and more details. This is the kitchen-sink approach, greatly facilitated by megaflops of computing power. Had Michaelis and Menten followed it, their model would have had buffers and pH dependence, they would have learned nothing, and their paper would have sunk without a trace. Their second lesson reveals a different approach, one ideally suited to biology at the molecular level. Models should be determined by the questions being asked and the data that are available. This is not to say that models might not get very complicated, if there are data to constrain them (Chen et al., 2009; Beard, 2011)—just that they remain contingent.

To some, this seems unbearably subjective. The point of all the mathematics, they say, is to make biology more like engineering—to become objective and predictive, not to wallow in subjective choices. There is no need to have a philosophical war about this (although it would be fun) because, at the end of the day, pragmatism trumps philosophy. There is really no choice when we move from the test tube to cells and organisms. Every model we make can capture only a tiny fraction of the reality that is present. We choose what to put in while leaving out everything else. Whether we admit it or not, we all follow Michaelis and Menten's second lesson. Let us not pretend to the world that we will eventually have predictive models of biology in the same way we have predictive models of airplanes.

Arturo Rosenblueth, the physiologist who was one of the cofounders with Norbert Weiner of cybernetics, hit the nail on the head when he quipped, “the best model of a cat is another cat, preferably the same cat.” Michaelis and Menten tell us not to worry; that is life. By making the right assumptions, a model may still be accurate and useful, even when it is not a cat.

The second lesson is enormously liberating: it gives us the freedom to formulate novel assumptions while relying on experimental confirmation for the final verdict. If we are not to be engulfed by mountains of data and want to relate the molecular to the physiological, we will need to make every use of that freedom.

Michaelis and Menten were a most unusual partnership for their time. Leonor Michaelis (1875–1949) introduced a generation of biologists to quantitative thinking through several influential books. He fell foul of German academic politics and found his way in 1929 to the Rockefeller Institute in New York, where he did pioneering work on free radicals (Michaelis et al., 1958). He was elected to the National Academy in 1943. In marked contrast, Maud Leonora Menten (1979–1960) was one of the first Canadian women to receive an MD, in 1911 at the University of Toronto. Bizarrely, PhDs were considered inappropriate for Canadian women (safer to cut up dead bodies than to learn how to think?), so she traveled to Berlin to work with Michaelis. She remained active in research for more than thirty years, with several significant contributions, but was promoted to full professor only in 1948, 2 years before she retired, (Skloot, 2000). The University was sufficiently abashed to later institute a memorial lecture and a chair in her honor. Too little, too late, one cannot help feeling. She was hardly conventional for her time and must have been a remarkable person as well as a fine scientist.

It is nearing the centenary of Michaelis and Menten's famous paper. From a biochemical perspective, it “stands up to the most critical scrutiny of informed hindsight” (Johnson and Goody, 2011). It does a lot more than that, as it continues to teach us how to use mathematics in the service of biological understanding.