Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2012 Feb 15;23(4):614–629. doi: 10.1091/mbc.E11-06-0584

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© 2012 Lacayo et al. This article is distributed by The American Society for Cell Biology under license from the author(s). Two months after publication it is available to the public under an Attribution–Noncommercial–Share Alike 3.0 Unported Creative Commons License (http://creativecommons.org/licenses/by-nc-sa/3.0).

“ASCB®,” “The American Society for Cell Biology®,” and “Molecular Biology of the Cell®” are registered trademarks of The American Society of Cell Biology.

PMC Copyright notice

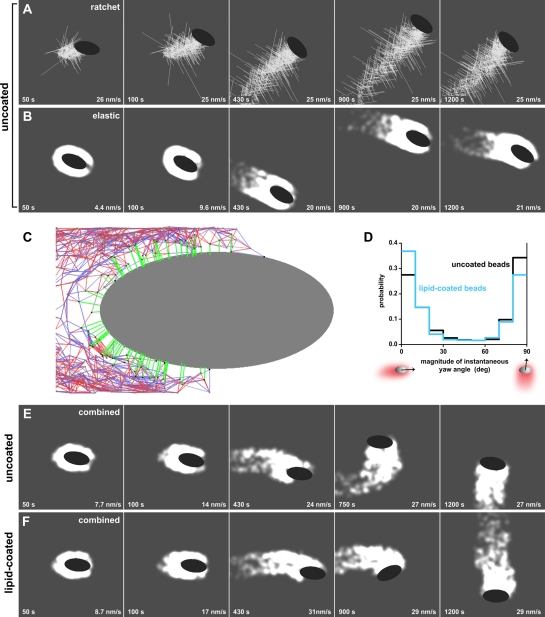
FIGURE 5: — A combined viscoelastic-ratchet model of actin polymerization recapitulates the migration of ellipsoidal beads. (A) Snapshots show a simulated ellipsoidal bead being propelled by actin filaments acting as ratchets with autocatalytic branching dynamics. The bead initiates motility in the parallel orientation and rapidly switches to migrating in the perpendicular orientation, where it remains during the length of the simulation. See also Video S4. (B) Simulations of a bead propelled only by a viscoelastic actin tail, without explicit filament ratchets, show that the bead exclusively migrates in the parallel orientation. The tail is illustrated by a continuous actin density so that the shading is proportional to the local number of actin network nodes. A lighter shade corresponds to higher density. See also Video S6. (C) Schematic of the combined viscoelastic-ratchet model depicts a migrating bead (gray) that is pushed by an actin network (red, blue, and green). The actin network is represented by a deformable node-and-spring network, at which growing filaments (green) are anchored. Network springs can be stretched (blue) or compressed (red). The springs break when a certain stretch-force threshold is exceeded. The nodes and springs also disassemble with a constant rate. The barbed end of each newly created filament grows against the bead surface exerting a pushing force, while the pointed end remains anchored at the network. All forces and torques generated by filament pushing and spring deformations are balanced. (D) The combined viscoelastic-ratchet model predicts a U-shaped distribution of instantaneous yaw-angle magnitudes for both uncoated (black line) and lipid-coated (cyan line) beads. The distribution for the lipid-coated beads is slightly skewed toward greater parallel orientation probability. (E) Simulations of an uncoated migrating bead using the combined viscoelastic-ratchet model show that the bead breaks symmetry in the parallel orientation and eventually switches to migrate in the perpendicular orientation (at ∼700 s). Note that the time for the fourth frame of this sequence does not correspond to the other panels. See also Video S8. (F) Simulations of a lipid-coated migrating bead using the combined viscoelastic-ratchet model with the same initial condition as in (E) show that the bead breaks symmetry in the parallel orientation and eventually switches to migrate in the perpendicular orientation (at ∼900 s). See also Video S9. Time: s. Speed: nm/s.