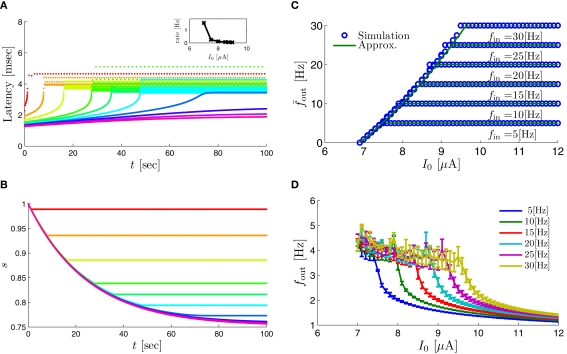
Figure A1.

Dependency on stimulation amplitude, I₀, in the fitted HHS model – (A) Spike latency as a function of time from stimulation onset (each color designates a different stimulation rate): stimulation at f_in = 25 Hz and I₀ = 7, 7.5, 8, 8.5, 8.75, 9, 9.25, 9.5, 9.75, 10 μA (red, orange…,); The transient slows down when I₀ is increased, and both initial and critical latencies change. Inset: the rate indeed decreases with I₀, and there exist two critical currents: $I_c^1,$ which is the minimal current to generate an AP (here $I_c^1\approx 6.9\mu A$) and $I_c^1$ which is the maximal current for which intermittent mode is reached (here $I_c^1\approx 9.25\mu A{I}_c^1,$). For $I_0>I_c^2$ the steady state is the stable mode. These results can be explained by (B) the sodium availability trace s(t) (using same color code as in A), where we see that when I₀ is increased then θ is decreased, while the transient rate of s is hardly affected. (C) Steady state firing rate ${\overline{f}}_{\text{out}}$ is 0 for $I_0<I_c^1\approx 6.9\mu A$ for all f_in. It then increases quadratically in I₀ during the intermittent mode, until ${\overline{f}}_{\text{out}}$ saturates when the stable mode is reached – at $I_c^2$ which depends on f_in. (D) Steady state latency dependence on I₀. For f_in = 25 Hz, the mean latency at steady state always decreases as a function of I₀. This mainly occurs since the latency function decreases with I₀ (Figure 3). However, during the intermittent mode, L ≈ L(θ), while θ decreases with current. Since L(s) is decreasing, this makes the decline of L in the intermittent mode less steep than in the stable mode, where $L\approx L\left(s_{\infty }^{+}\right)$ and $s_{\infty }^{+}$ does not change with I₀. Here we also see that the latency fluctuations in the intermittent mode are much larger than in the stable mode.