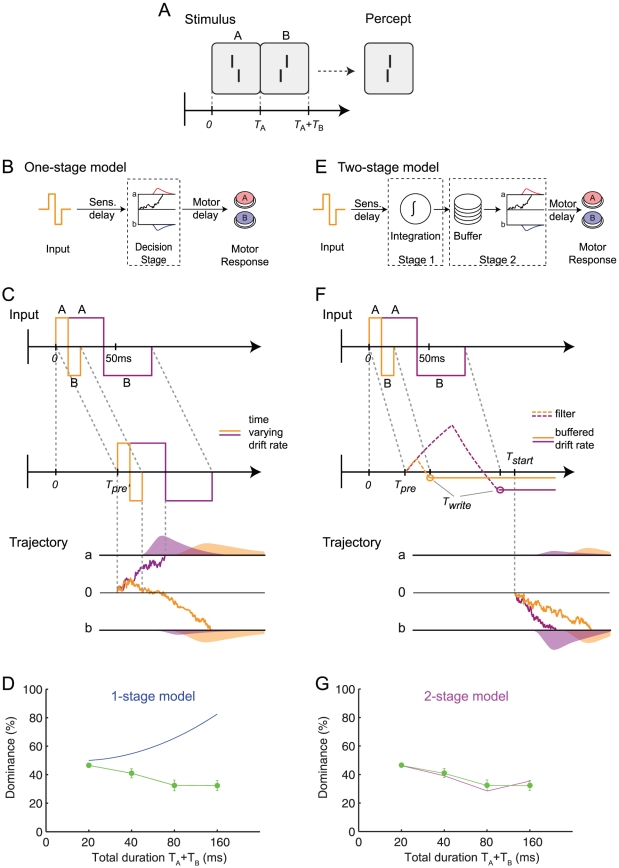
Figure 2. One-stage and two-stage models of decision making.
(A) A vernier (stimulus ‘A’) is followed by a second vernier (stimulus ‘B’). The first vernier is either offet to the right (as shown) or to the left (not shown). The second vernier stimulus is always offset to the opposite side. Only one vernier is perceived and the offsets of the two vernier stimuli fuse. The perceived offset of the fused vernier is more strongly influenced by the second than the first vernier when the duration 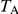 and
and 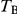 of stimulus ‘A’ and ‘B’ are equal,
of stimulus ‘A’ and ‘B’ are equal, 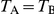 . (B) One-stage model. After a sensory delay, the stimulus input is directly fed into the decision stage as the drift rate of a decision variable which is subject to a random walk. When the decision variable hits the upper boundary (
. (B) One-stage model. After a sensory delay, the stimulus input is directly fed into the decision stage as the drift rate of a decision variable which is subject to a random walk. When the decision variable hits the upper boundary ( ), the decision is for the offset of the first vernier (stimulus ‘A’). When it hits the lower boundary (
), the decision is for the offset of the first vernier (stimulus ‘A’). When it hits the lower boundary (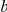 ), the decision is for the offset of the second vernier (stimulus ‘B’). A motor response is executed accordingly. Variability in the drift leads to different reaction times (red and blue curves show reaction time distributions). It is important to note that observers push one button for left responses and one for right responses. In this figure, however, button ‘A’ is a symbol denoting responses according to the first vernier stimulus (either left or right) and button ‘B’ according to the second vernier stimulus. (C) Upper panel: After preprocessing and signal transmission of duration
), the decision is for the offset of the second vernier (stimulus ‘B’). A motor response is executed accordingly. Variability in the drift leads to different reaction times (red and blue curves show reaction time distributions). It is important to note that observers push one button for left responses and one for right responses. In this figure, however, button ‘A’ is a symbol denoting responses according to the first vernier stimulus (either left or right) and button ‘B’ according to the second vernier stimulus. (C) Upper panel: After preprocessing and signal transmission of duration 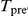 (sensory delay), the one-stage model translates the time course of the input directly into a time-varying drift rate of the decision process. Bottom panel: The time-varying drift rate directly drives the drift-diffusion process leading to trajectories which first increase and then decrease (orange trajectory,
(sensory delay), the one-stage model translates the time course of the input directly into a time-varying drift rate of the decision process. Bottom panel: The time-varying drift rate directly drives the drift-diffusion process leading to trajectories which first increase and then decrease (orange trajectory, 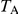 = 10 ms; purple,
= 10 ms; purple, 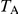 = 40 ms). The earlier the decision variable hits one of the boundaries, the faster the reaction times. For short
= 40 ms). The earlier the decision variable hits one of the boundaries, the faster the reaction times. For short 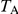 (e.g. 10 ms) the trajectory does not reach any of the boundaries (
(e.g. 10 ms) the trajectory does not reach any of the boundaries ( ,
, 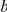 ) during stimulus presentation. One of the boundaries is reached after a random walk (orange line and reaction time distributions). For longer durations, the trajectory (purple line) more likely hits the upper than the lower boundary, leading to a decision for stimulus ‘A’. In few cases, a decision for stimulus ‘B’ is made because of the noise (purple reaction time distributions). (D) Experiment 1. In the psychophysical experiments, dominance is quantified as the percentage of responses which are in accordance with the first vernier. According to the one-stage model, vernier dominance increases when total stimulus duration increases (blue line), in stark contrast to the performance of human observers (green line; mean dominance across observers; error bars represent standard error of means, SEM). For the model, dominance is quantified as the percentage of trials in which the diffusion process hits the upper boundary (
) during stimulus presentation. One of the boundaries is reached after a random walk (orange line and reaction time distributions). For longer durations, the trajectory (purple line) more likely hits the upper than the lower boundary, leading to a decision for stimulus ‘A’. In few cases, a decision for stimulus ‘B’ is made because of the noise (purple reaction time distributions). (D) Experiment 1. In the psychophysical experiments, dominance is quantified as the percentage of responses which are in accordance with the first vernier. According to the one-stage model, vernier dominance increases when total stimulus duration increases (blue line), in stark contrast to the performance of human observers (green line; mean dominance across observers; error bars represent standard error of means, SEM). For the model, dominance is quantified as the percentage of trials in which the diffusion process hits the upper boundary ( ). (E) Two-stage model. The input is first integrated, before it is buffered and fed as a constant drift into the drift-diffusion process. (F) The input is delayed by
). (E) Two-stage model. The input is first integrated, before it is buffered and fed as a constant drift into the drift-diffusion process. (F) The input is delayed by 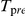 and integrated with a leak. The value of the first stage is read out after stimulus termination
and integrated with a leak. The value of the first stage is read out after stimulus termination 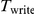 , written into a buffer, and fed as a constant drift rate into the diffusion process at times greater than
, written into a buffer, and fed as a constant drift rate into the diffusion process at times greater than 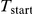 . Longer input durations lead to stronger negative drifts. Hence, the probability to hit the lower boundary
. Longer input durations lead to stronger negative drifts. Hence, the probability to hit the lower boundary 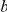 increases with increasing vernier durations. (G) Performance of the two-stage model (purple line) is similar to the performance of human observers for total durations up to 80 ms (green circles, same human data as in D).
increases with increasing vernier durations. (G) Performance of the two-stage model (purple line) is similar to the performance of human observers for total durations up to 80 ms (green circles, same human data as in D).