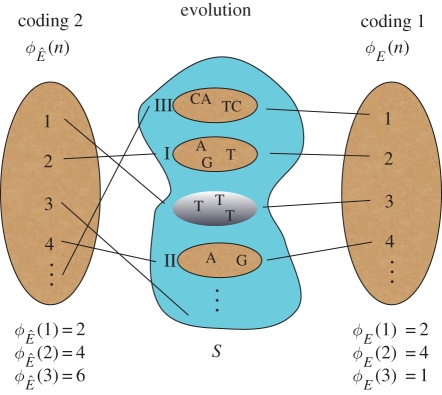
Figure 1.

A schematic of the coding of population states, and the theorem. The middle irregular shape represents the space of population states, S, with four states depicted (the ovals). Roman numerals indicate the time when each state is visited during evolution (the silver-shaded state, s = {T,T,T}, is never visited). Vertical ovals on the right and left represent two different codings by the positive integers, along with their respective evolutionary mappings, ϕ_E(n) and 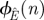, over the first three time steps. If evolution is progressive, then coding 2 is possible, and the theorem then says that we can ‘decide’ any population state, s ∈ S. For example, we can decide state ‘T,T,T’ by finding its code (i.e. ‘1’), and then iterating the map, 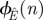, until we obtain an output greater than ‘1’ (this occurs at time step 1 because 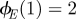). If ‘1’ has not yet been visited by this time, it never will be. Conversely, if all population states are decidable, then, under coding 1, we can apply the algorithm provided in part 2 of the theorem's proof to obtain coding 2, thereby demonstrating that evolution is progressive.