Abstract
Conservation investments are increasingly being implemented through payments for ecosystem services (PES) for the protection and restoration of ecosystem services around the world. Previous studies suggested that social norms have substantial impacts on environmental behaviors of humans, including enrollment of PES programs. However, it is still not well understood how social norms are affected by the design of PES programs and how the evolution of social norms may affect the efficiency of conservation investments. In this paper, we developed an agent-based simulation model to demonstrate the evolution and impacts of social norms on the enrollment of agricultural land in a PES program. We applied the model to land plots that have been enrolled in China’s Grain-to-Green Program (GTGP) to examine reenrollment in an alternative payment program when the current payments ceased. The study was conducted in Wolong Nature Reserve where several thousand plant and animal species, including giant pandas, may benefit from the reenrollment. We found that over 15% more GTGP land can be reenrolled at the same payment if social norms were leveraged by allowing more than ten rounds of interactions among landholders regarding their reenrollment decisions. With only three rounds of interactions, an additional 7.5% GTGP land was reenrolled at the same payment due to the effects of social norms. In addition, the effects of social norms were largest at intermediate payments and were smaller at much higher or much smaller payments. Even in circumstances where frequent interactions among landholders about their enrollment decisions are not feasible, policy arrangements that divide households into multiple waves for sequential enrollment can enroll over 11% more land at a given payment level. The approach presented in this paper can be used to improve the efficiency of existing PES programs and many other conservation investments worldwide.
Keywords: agent-based model, conservation investments, Grain-to-Green Program, payments for ecosystem services, social norms
1. Introduction
Current conservation investments are inadequate for conserving ecosystems globally (James et al., 1999; James et al., 2001), raising concerns about the efficiency of conservation investments (Ferraro and Simpson, 2002). One approach to improve the efficiency of conservation investments is through Payments for Ecosystem Services (PES). PES programs have increasingly been implemented in many countries (OECD, 1997; Wunder, 2008) through the provision of economic incentives to key stakeholders to undertake actions for desired environmental benefits or reduce actions that are harmful to the environment (Wunder, 2007; Jack et al., 2008). Previous studies of collective action in natural resources management have found that social norms are important for the sustainable use of common-pool resources (Ostrom, 2000; Dietz et al., 2003). In fact, social norms have been demonstrated to have substantial impacts on the enrollment of PES programs (Chen et al., 2009a). However, little is known about how different types of conservation programs may shape the creation of social norms, and how the evolution of social norms may in turn affect the efficiency of conservation investments (Sengupta et al., 2005).
At the broadest level, social norms can be defined as shared understandings of how individual members in a community will behave in a given circumstance (Coleman, 1990; Bendor and Swistak, 2001). The term “social norms” is frequently used to describe two different kinds of social phenomena- injunctive norms and descriptive norms (Cialdini et al., 1990; Cialdini, 2003). Injunctive norms specify what people ought to do (or ought not do), which involve morally approved and disapproved behavior (Cialdini, 2003). Although the microfoundations of compliance with injunctive norms are poorly understood, past studies have shown that injunctive norms influence human behavior due to internalized social-psychological values such as reputation, fairness, and self-esteem (Elster, 1989; Fehr and Gintis, 2007; Goldstein et al., 2008). In contrast, descriptive norms can be defined simply as what most people in a given situation usually do, that is, they define normal behavior. Although descriptive norms may be motivated by compliance with internalized moral prescriptions, they may also simply be the result of an equilibrium in which economically rational agents choose actions based on the expected actions of others (Young, 1996). In this study, we focus on explaining the effect of descriptive social norms on decisions regarding reenrollment in PES programs, as well as on understanding the effect of different PES program designs on the emergence of descriptive social norms (which are referred to as social norms hereafter).
In the context of participation in PES programs, through interactions among stakeholders and observations of other’s behavior, social norms can emerge, and information on social norms can be obtained. Since most of the interactions among stakeholders are at the local neighborhood level (Case, 1992; Foster and Rosenzweig, 1995), social norms that emerge through these interactions can be heterogeneous across neighborhoods due to heterogeneities in their environmental and socioeconomic conditions. Although recent studies on conservation investments are beginning to incorporate some of these spatial heterogeneities (Siikamaki and Layton, 2007; Chen et al., 2010), they were not able to take into consideration the dynamics of stakeholders’ decision-making due to the evolution of social norms over time and of stakeholders’ capability of learning information on social norms through interactions with other stakeholders. This was partly due to challenges in integrating cross-scale and cross-disciplinary data and methods (Parker et al., 2003; An et al., 2005). In particular, existing data and analytic approaches make it difficult to identify the impact of program design on social norms and the effect of variation in social norms on the participation in conservation programs.
One approach to overcome these limitations has been to utilize agent-based modeling (ABM) to simulate the effect of a variety of social and environmental factors on the emergence and evolution of social norms. ABM is a bottom-up approach that predicts emergent higher-level outcomes by simulating decision-making of individuals (e.g., persons or households), and their interactions with each other and with their environment (An et al., 2005; Matthews et al., 2007). Agents usually have knowledge of their local environment, and are capable of interacting with other agents to learn others’ actions and perceive norms. Based on these interactions, agents may change their actions to increase their utility and/or conform to social norms (Manski, 2000; Vincent, 2007), which in turn may change social norms. Since most of these interactions are local, agents may be aware that there are uncertainties in their perceived social norms. To reflect these uncertainties, the perceived social norms of agents may be a combination of the norm in the community and a random norm (Epstein, 2001). As agents continue interacting with other agents, uncertainties in their perceived norms can be reduced (Carley, 1986; Parker et al., 2003). Because of these features, ABM has been successfully applied in studies of social norms (Epstein, 2001; Gotts and Polhill, 2009) and in coupled human-nature systems (CHANS) studies (Deadman et al., 2004; Liu et al., 2007; Matthews et al., 2007).
We examine the effects of social norms on enrollment in China’s Grain-to-Green Program. The Grain-to-Green Program [GTGP, also referred to as the Sloping Land Conversion Program (Xu et al., 2006; Liu et al., 2008)] has been implemented since 1999 to convert sloping cropland to forest or grassland. Due to its main objective of reducing soil erosion by increasing vegetative cover, the criterion for land conversion in the GTGP is for the slope of cropland in southwestern China to be >25° and cropland in northwestern China to be >15°. Participating farmers receive conservation payment for a maximum of eight years. The government offers farmers an annual payment of 2,250 kg and 1,500 kg of grain or cash payments of 3,150 and 2,100 yuan per ha of enrolled cropland in the upper reaches of the Yangtze river basin and in the middle-upper reaches of the Yellow river basin, respectively (as of July, 2011, 1 USD = 6.4 yuan). In addition, annual miscellaneous expenses of 300 yuan per ha and a one-time subsidy of 750 yuan per ha for seeds or seedlings were provided. By the end of 2006, the GTGP had converted about 9 million ha of cropland (Liu et al., 2008). Studies have shown that the GTGP has substantially improved ecosystem services such as increased forest cover, reduced water surface runoff and soil erosion, reduced river sediments and nutrient loss for maintaining soil fertility, and reduced desertification (Liu et al., 2002; Ma and Fan, 2005; Li et al., 2006; Liang et al., 2006; Long et al., 2006; Xu et al., 2006; Wang et al., 2007). While these conservation gains are encouraging, the cost of the GTGP has also been substantial. By the end of 2005, over 90 billion yuan had been invested in the GTGP, and it is expected that the total investment in the GTGP reached 220 billion yuan by the end of 2010 (Liu et al., 2008). The GTGP contracts began to mature in 2008. To sustain the conservation gains from the GTGP, the program was extended for another cycle of up to eight years.
In this paper, we develop an agent-based model to simulate the effects of social norms on land enrollment in a PES program and the effects of PES program design on patterns of social norm emergence and evolution. We used data from household surveys and government documents to parameterize the decision-making of landholders for enrollment, and satellite imagery to map and model the locations of land for potential enrollment. We measured the effects of social norms by comparing land enrollment at different times allowing for updating perceptions of social norms from different rounds of interactions among landholders. We also explored the effects of different program designs on the emergence of social norms. Our model was used to demonstrate the effects of social norms on the reenrollment of sloping agricultural land plots that have been enrolled in China’s Grain-to-Green Program (GTGP) in Wolong Nature Reserve.
2. Material and methods
2.1. Study area
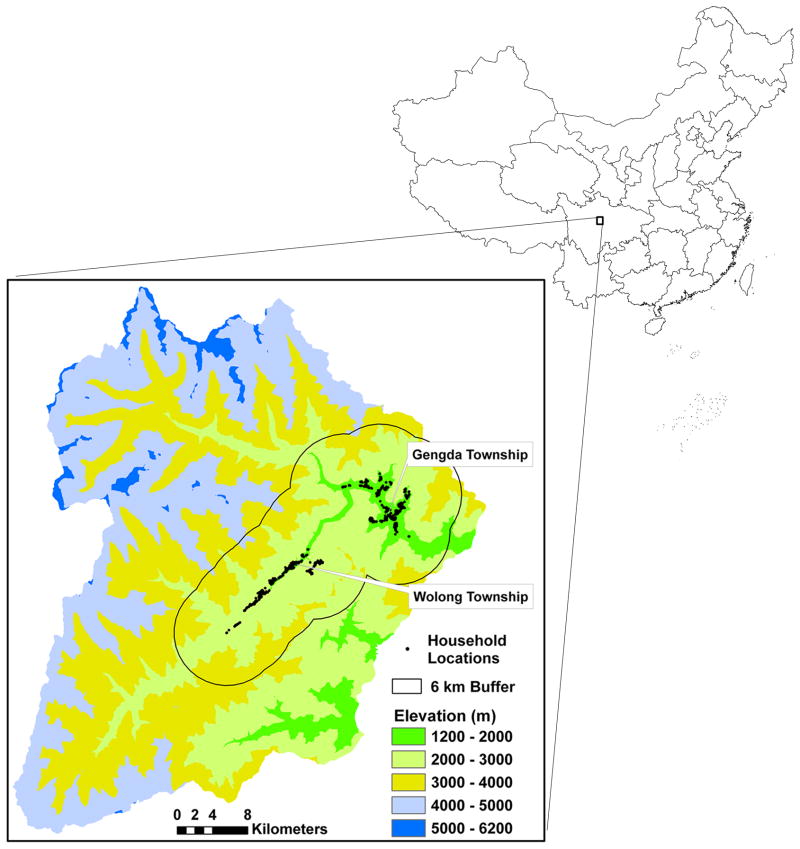
Located in China’s southwest Sichuan province, Wolong Nature Reserve (Fig. 1) is within one of the world’s top global biodiversity hotspots (Myers et al., 2000; Liu et al., 2003). As a flagship nature reserve for the protection of about 10% of the world-famous endangered giant pandas (Ailuropoda melanoleuca) in the wild, Wolong Nature Reserve also provides habitat to more than 6,000 plant and animal species (Liu et al., 2007). In addition, about 4,500 indigenous people in about 1,200 households (>90% of them are farmers) live in two townships (Gengda and Wolong) within the reserve (Fig. 1). In addition to farming, local residents engage in diverse economic activities including fuelwood collection, road construction, and tourism development. The main human activities that caused rapid degradation in the local ecosystem were deforestation for agricultural land, and timber and fuelwood harvesting (Liu et al., 2001; An et al., 2002). In Wolong Nature Reserve, the GTGP enrollment took place in 2000, 2001, and 2003. In addition to many cropland plots with slopes over 25°, some cropland plots with slopes below 25° were also allowed to enroll. Participating households receive an annual payment of 3,450 yuan per ha for eight years.
Fig. 1.
Locations and elevations of Wolong Nature Reserve and indigenous households in the reserve.
2.2. Data
We randomly selected 321 out of about 1,200 households for interviews with household heads or their spouses in the summer of 2006, resulting in 304 valid interviews (95% response rate). We collected information on land-use plans of landholders regarding each of their land plots that were enrolled in the GTGP after the payments ceased. These households held a total of 735 GTGP plots (110.4 ha), and households planned to reconvert 166 (22.6%) GTGP plots to crop production after the payments ceased (Chen et al., 2009a). At the household level, 98 (32.2%) households planned to reconvert at least some of their GTGP plots after the payments ceased (Chen et al., 2009b). The households with GTGP plots that they planned to reconvert to crops were further questioned to elicit their potential reenrollment under alternative policy scenarios. Policy scenarios included payment level and neighbors’ behavior (i.e. percentage of neighbors reconverting at least one of their GTGP plots). Payment level took three possible values: 1,500, 3,000, and 4,500 yuan per ha. The highest value (4,500 yuan per ha) was adjusted to 3,750 yuan per ha after the first quarter of the survey to allow for more variation in responses. Neighbors’ behavior also took three possible values, for which respondents were told that 25%, 50%, or 75% of their neighbors would reconvert at least part of their GTGP plots. Since no moral judgment (i.e. what people ought or ought not to do) was associated to landholders’ reenrollment decisions, our study on social norms using neighbors’ behavior is a study on descriptive norms (Cialdini et al., 1990). Neighbors were defined as households who lived in the same group (an administrative unit within a village in rural China) because households in the same group tend to live closer and have more interactions with each other, which are important for social norms to be formed and sustained (Coleman, 1990; Cialdini and Goldstein, 2004). We used stated-choice methods (Louviere et al., 2000) to relate policy attributes (payment level and neighbors’ behavior) to the reenrollment of GTGP plots. Instead of using all possible combinations of policy attributes, we used a main effects design in which policy attribute arrays are orthogonal to one another to more efficiently understand the main effect of each attribute.
For all households in the reserve, we obtained a complete inventory of their characteristics, including area of each of their GTGP plots (from the GTGP land statistics), household size, age and gender of the household head from local government documents (Chen et al., 2010). We also measured the geographic location of each household using real-time differentially corrected Global Positioning System (GPS) receivers. For the reserve, a total of 2,470 plots, comprising 367.5 ha and belonging to 969 households, were enrolled in the GTGP. However, geographic locations of all these plots were not available. We therefore measured the geographic locations of 735 GTGP plots that were enrolled by the 304 households that we sampled for interviews using real-time differentially corrected GPS receivers. Locations of these 735 plots were used together with remotely sensed imagery and topographic data for the identification of all GTGP plots in the reserve.
2.3. Model description
We present our agent-based model in accordance with the ODD (Overview, Design concepts, and Details) protocol (Grimm et al., 2006; Grimm et al., 2010).
2.3.1. Purpose
This model has been developed to simulate the effects of social norms on land enrollment in a PES program and the effects of PES program design on patterns of social norm emergence and evolution.
2.3.2. Entities, state variables, and scales
In our model, agents are individual households, and agents were the main entities. Agents are characterized by the state variables: household_identity_number, group_identity_number (in which the household is located), household_size, cropland, GTGP_land, household_head_age, household_head_gender, township, X and Y coordinates of households, perceived_social_norm, knowledge (of social norms) and learn (about social norms). GTGP land parcel entity is characterized by the state variables: GTGP_parcel_identity_number, household_identity_number (in which the GTGP parcel belongs to), area, slope, elevation, and X and Y coordinates of the location of GTGP parcels. The geographic extent of the overall model is a 6-km buffer around the exact locations of all households (Fig. 1), in which all the GTGP plots were stochastically distributed. The model was run for 15 time steps because the dynamics of GTGP land reenrollment due to the effects of social norms tend to converge within 15 time steps.
2.3.3. Process overview and scheduling
In our model, PES contracts last for one unit of time. The length of a time unit is not specified because it can be different among different PES programs, and is irrelevant in this study. The model was run across multiple units of time to allow for multiple opportunities for household agents to make reenrollment decisions. At the beginning of each simulation, all the GTGP plots are stochastically distributed through the mapping GTGP plots submodel. At each time step, household agents make decisions regarding the reenrollment of each of their GTGP plots and would reenroll a GTGP plot in the PES program if the payment is larger than the opportunity cost of the plot. The opportunity cost of each GTGP plot was stochastically determined on the basis of agents’ perceived_social_norm, the proposed conservation payment, and socioeconomic characteristics of an agent and characteristics of the GTGP plot through the GTGP reenrollment submodel. Although the payment level is not changed throughout the course of each simulation and socioeconomic characteristics of agents remain constant, agents may perceive different social norms at different times due to the impact of social norms on agents’ reenrollment decisions. After the initialization (time = 1), the value of perceived_social_norm for each agent is updated at each time (time = t and t > 1) on the basis of the social norms in the group at a previous time (time = t − 1), and the agent’s knowledge of and learn about social norms. The value of knowledge for each agent is also updated through learn about social norms. Perceived_social_norm and knowledge are updated in the dynamics in GTGP reenrollment submodel. The order of household agents in which the value of perceived_social_norm is updated is irrelevant.
2.3.4. Design concepts
Emergence
Emergent phenomena included nonlinearity in the effects of social norms on land reenrollment and convergence of land reenrollment after several rounds of interactions among agents.
Adaptation
Agents adapted to changes in the perceived_social_norm by changing their reenrollment decisions.
Objective
Agents’ objective was to maximize their utility in making reenrollment decisions.
Interaction
Agents who are located in the same groups interact among each other to perceive social norms about land reenrollment. Interactions among agents are represented as agents can perceive social norms of land reenrollment at previous time steps.
Learning
Agents may learn about other agents’ actions, perceive social norms, and update their own actions. The learning process is implemented by combining the perception about social norms and calibration of the impact of social norms on the PES program enrollment. The perceived_social_norm of agents is represented as an aggregation of the social norms of the agent’s group and a random norm weighted by the agent’s knowledge about social norms. Agents’ knowledge about social norms can be increased through additional rounds of interactions. Each agent’s enrollment decision is then updated by applying the updated perceived_social_norm in the GTGP reenrollment submodel.
Sensing
In addition to the perceived_social_norm, agents are assumed to know their own status (characterized by their state variables) on which their land reenrollment decisions are based.
Stochasticity
Since we do not have information about locations of all the GTGP plots, we stochastically distributed them across the landscape. The opportunity cost of each GTGP plot was also determined stochastically because we could only model the probability of households reenrolling each of their GTGP plots. In addition, the perceived_social_norm of agents after the first time step was also represented stochastically as a weighted aggregation of the social norms of the agent’s group and a random norm.
Observation
The total amount of GTGP land reenrollment over time was recorded for model analysis.
2.3.5. Initialization
A total of 969 agents and 2,470 GTGP plots were created for each simulation. Agents’ characteristics were initialized with data collected for households’ locations and socioeconomic characteristics. All the GTGP plots were determined through the mapping GTGP plots submodel, and were characterized with the GTGP land statistics data and a digital elevation model dataset. The value of perceived_social_norm for all households is initialized as 0.5, representing the mean of a uniform distribution over landholders’ perception of the share of neighbors that will reconvert GTGP plots. The initial values for knowledge (i.e. initial_knowledge) and learn were chosen arbitrarily due to lack of information on these variables. However, to explore the effects of the uncertainties in these variables, the model was simulated under different levels of initial_knowledge and learn.
2.3.6. Input data
The model does not use input data to represent time-varying processes.
2.3.7. Submodels
Our model is consisted of three submodels. Mapping GTGP plots submodel was used to distribute all the GTGP plots across the landscape. In the GTGP reenrollment submodel, household agents make reenrollment decisions regarding each of their GTGP plots. Dynamics in GTGP reenrollment due to changes in social norms of land reenrollment were modeled in the dynamics in GTGP reenrollment submodel. At the beginning of each simulation, the mapping GTGP plots submodel was executed for the initialization of the model. At each time step, the GTGP reenrollment submodel was executed to determine the land reenrollment. The dynamics in GTGP reenrollment submodel was also executed at each time step to update the GTGP reenrollment by updating the value of perceived_social_norm and applying the updated perceived_social_norm to the GTGP reenrollment submodel.
2.3.7.1. Mapping GTGP plots
We used a fuzzy classification algorithm based on the principle of maximum entropy (Jaynes, 1957) and multispectral data to develop a map of the probability that each grid cell (i.e., pixel) is enrolled in the GTGP using the software MaxENT (Phillips et al., 2006). Our multispectral data consist of two Landsat Thematic Mapper (TM) images (28.5m × 28.5m /pixel) acquired on April 19 and September 18, 2007, and topographic data including elevation, slope and aspect derived from a digital elevation model (with the same pixel resolution as the Landsat TM imagery). We randomly selected two-thirds of the 735 GTGP plots, for which we have geographic locations, to calibrate the classification algorithm, and one-third to validate the output map. Since all of the 735 GTGP plots that we measured are located within 6 km of their corresponding households, the probability map (Chen et al., 2010) was developed in a 6-km buffer around all household locations. We validated the GTGP probability map using a receiver operating characteristic (ROC) curve (Hanley and Mcneil, 1982) based on the validation data set and 10,000 randomly selected pixels (Wiley et al., 2003; Phillips et al., 2006). The resulting area under the ROC curve (AUC) was 0.98 (SD = 0.001) and was significantly (p < 0.001) different from 0.5 (Delong et al., 1988). This suggests a high accuracy of the GTGP probability map (Chen et al., 2010).
We stochastically distributed all the 2,470 GTGP plots in the reserve across the landscape based on the GTGP probability map (Chen et al., 2010) and the probability distribution of the distances between the 735 GTGP plots that we measured and their corresponding households. The resolution of the GTGP probability map was resampled to 10 meters so that each GTGP plot occupied at least one pixel. To distribute a GTGP plot in the landscape, we took three steps. First, we randomly determined a plot’s distance to its corresponding household based on the exact sample probability distribution of the distances between the 735 GTGP plots and their corresponding households. Second, from all the pixels that are at the specified distance from the household, we randomly chose a pixel as the central pixel of the GTGP plot based on these pixels’ probability values of being GTGP land (i.e. from the GTGP probability map). Third, given the central pixel, any neighboring pixels that have positive probability of being GTGP land were included as part of the GTGP plot until the area of the GTGP plot was reached.
2.3.7.2. GTGP reenrollment
The probability of a GTGP plot being reenrolled was calculated as:
| (1) |
where P(reenrolli) is the probability of the ith GTGP plot being reenrolled in a new payment program, P(reconverti) is the probability of the ith GTGP plot being reconverted to crop production after the payments cease, and P(reenrolli | pay > 0, reconvert) is the probability of reenrolling the ith GTGP plot in a new payment program for those plots that will be reconverted to crop production after the payments cease. We modeled both P(reconverti) and P(reenrolli | pay > 0, reconvert) from Eq. 1 as two different functions of the same household and plot characteristics (See Table 1). The probability of a GTGP plot being reconverted to crop production after the payments cease ( P(reconverti) in Eq. 1) was modeled on the basis of features of GTGP land plots and household characteristics of landholders using a logistic regression (Chen et al., 2010):
where households who had larger size, enrolled less land in the GTGP, and lived in the Wolong township were significantly more likely to reconvert their GTGP plot. Next, the probability of reenrolling a GTGP plot in a new payment program for those plots that will be reconverted to crop production after the payments cease (i.e. P(reenrolli | pay > 0, reconvert) in Eq. 1) was estimated with a pooled logit model on the basis of neighbors’ behavior (representing social norms), conservation payment, features of GTGP land plots and household characteristics of landholders using data that were collected through household interviews (Table 1). We corrected for dependencies among GTGP plots of the same landholder and among responses to different policy scenarios for the same plot using Huber’s variance correction to obtain robust standard errors for clustered data in the logit model (Wooldridge, 2002). Neighbors’ behavior had significant impacts on the respondents’ intention of reenrolling their GTGP plots in PES programs (Table 1). It was estimated that an additional 10% of neighbors’ reconverting at least part of their GTGP plots to crop production reduced the respondents’ intentions of reenrollment by 3.5% on average. This result suggests that people’s re-enrollment intentions are influenced by the reenrollment decisions of their neighbors and tend to conform to the majority. Higher payments were more likely to induce land plots in a PES program. In addition, households who had smaller size, owned more cropland, and had an older household head were more likely to reenroll their GTGP plots that will be reconverted to crop production after the payments cease (P(reenrolli | pay > 0, reconvert) in Eq. 1).
Table 1.
Pooled logit estimation of reenrollment of GTGP plots in a PES program.
| Independent variables | Description | Parameters (Robust standard errors) | Marginal effects |
|---|---|---|---|
| Neighbors’ behavior | proportion of neighbors’ reconverting GTGP plots | −1.409*** (0.438) | −0.351 |
| Ln(payment) | payment in yuan | 1.893*** (0.311) | 0.471 |
| Household size | number of members | −0.387** (0.144) | −0.096 |
| Cropland | ha | 3.677** (1.165) | 0.916 |
| GTGP land | land enrolled in the GTGP (ha) | 0.359 (0.867) | 0.089 |
| Household head age | years | 0.034** (0.013) | 0.008 |
| Household head gender | female=1; male=0 | −0.321 (0.473) | −0.080 |
| Township | Gengda=1; Wolong=0 | 0.066 (0.527) | 0.016 |
| Area | ha | 0.912 (1.201) | 0.227 |
| Slope | degree | 0.017 (0.021) | 0.004 |
| Elevation | 100 m | −0.004 (0.135) | −0.001 |
| Distance | 100m | −0.105* (0.042) | −0.026 |
| Constant | −9.530** (3.155) | ||
| χ2 | 61.23*** |
Observations = 498; Number of plots = 166;
p≤0.05;
p≤0.01;
p≤0.001
The opportunity cost of each plot was determined using a Bernoulli trial, with P(reenrolli) in Eq. 1 as the rate parameter, which determined reenrollment of plots as a function of neighbors’ behavior and payment (Eq. 1). The opportunity cost of a plot is the payment level at or above which the plot will be reenrolled. Agents are then assumed to reenroll GTGP plots in a PES program if the payment level is equal to or larger than their opportunity costs.
2.3.7.3. Dynamics in GTGP reenrollment
We assumed that land plots that are reenrolled in PES programs are contracted for one unit of time, and all agents make reenrollment decisions for all of their GTGP plots at each time point. GTGP plots are reconverted if they are not reenrolled in PES programs. The payment of PES programs was modeled using a parameter, payment, with a default value of 3,000 yuan per ha. At the beginning (time = 1), the value of social norms for all households is 0.5, representing the mean of a uniform distribution over landholders’ perception of the share of neighbors that will reconvert GTGP plots. At any other time (time = t and t > 1), the value of social norms for each agent is determined by the proportion of its neighbors (households living in the same group) reconverting at least part of their GTGP plots back to crop production at a previous time (time = t − 1).
Because agents cannot obtain complete information on social norms through one round of interactions, the perceived_social_norm of agents is represented as a weighted aggregation of the social norms of the agent’s group and a random norm (Epstein, 2001). That is, perceived_social_norm j = social_norm j * knowledge j + random_norm * (1-knowledge j), where perceived_social_norm j is the perceived social norm of the jth agent, social_norm j is the social norms in the group where the jth agent is located in, and knowledge j is the jth agent’s knowledge about social norms. Knowledge ranges between 0 and 1, and the default value of the initial_knowledge (knowledge obtained from the first round of interactions) is 0.3. As agents continue interacting with each other when the time step moves forward, they may obtain more knowledge about others’ actions (Carley, 1986; Parker et al., 2003). The knowledge of agents about social norms increases by a magnitude of learn (with a default value of 0.1) through each additional round of interactions in each time step until full knowledge’ is obtained (i.e. when knowledge = 1). The default values of parameters, payment, initial_knowledge, and learn were chosen arbitrarily in our model, and should be changed for applications under different social contexts when such information is available. Once the perceived_social_norm is updated, each agent then updates its reenrollment decision by applying the updated perceived_social_norm in the GTGP reenrollment submodel.
2.4. Simulation experiments
We applied different levels of payments for a one-time reenrollment to construct the relationship between payment and the amount of GTGP land that can be reenrolled. To demonstrate the effects of social norms, households repeatedly make reenrollment decisions for all of their GTGP plots at each time point for a total of 15 time units, which allowed up to 14 rounds of interactions among landholders to perceive their neighbors’ reenrollment decisions at a previous time.
In another set of simulations for exploring the effects of social norms, all of households make reenrollment of their GTGP plots only once, and households were randomly and equally divided into different waves for reenrollment at different times. Under this approach, the first wave of households makes reenrollment decisions with a flat prior for the perception of their neighbors’ reconversion decisions (i.e. the value of social norms for these households is 0.5). All other waves of households make their reenrollment decisions where social norms are the reconversion decisions of their neighbors who have already made reenrollment decisions. The total number of waves for reenrollment ranged from 1 to 15, where 1 means all households make reenrollment decisions at the same time (i.e. households were not divided into waves), and 15 means all households were divided into 15 waves for reenrollment at different times. The more waves the households were divided into, the more rounds of interactions occur for households who make reenrollment decisions at a later time.
Our model was developed using the Java programming language (JDK 1.4.2, Sun Microsystems). Because of stochastic processes in spatial distributions of GTGP plots, reenrollment decision-making and perception of social norms, our model was run 100 times using each of the parameter settings. We report the mean values of results from 100 runs. In our results, we present reenrollment outcomes for only those GTGP plots that required payment for reenrollment, although all of households and their GTGP plots were used for calculating social norms.
3. Results
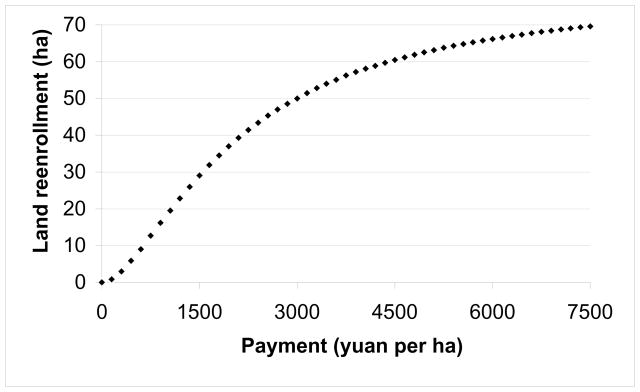
The total amount of GTGP land that required payment for reenrollment was about 77.9 ha, and different amounts of this GTGP land can be reenrolled at different payment levels (Fig. 2). It was estimated that about 44.3% of GTGP land can be reenrolled at 1,800 yuan per ha, which is about half of the payment in the current GTGP. If the current GTGP payment (3,450 yuan per ha) was offered, about 69.3% of the GTGP land can be reenrolled. However, reenrollment of most GTGP land can be expensive. For instance, reenrollment of 90% of GTGP land requires a payment of about 7,500 yuan per ha.
Fig. 2.
Amount of GTGP land that can be reenrolled at different payments.
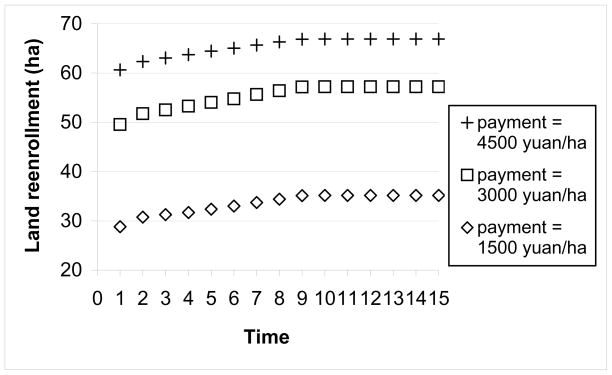
When the effects of social norms are considered in landholders’ decision-making of reenrollment, land reenrollment at a given payment depends on social norms at any point in time (Fig. 3). Compared to the reenrollment when time = 1, more GTGP land can be reenrolled at a later time (i.e. time > 1) when previous interactions and observations lead to updates on the agent’s perception of neighbor’s behavior. For instance, at a payment of 3,000 yuan per ha, 7.5%, 12.3% and 15.5% more GTGP land can be reenrolled when time = 4, 7, 10 due to the effects of social norms that were perceived through 3, 6, and 9 rounds of interactions, respectively (Fig. 3). Two-sample t tests showed that these increases were statistically significant (p-values < 0.001). The increment in the reenrollment of GTGP land due to additional rounds of interactions among landholders was decreasing. Through the first three rounds of interactions at a payment of 3,000 yuan per ha, the reenrollment of GTGP land increased by 7.5%, reaching a reenrollment of 53.3 ha when time = 4. During time 4 through 7 and 7 through 10, there were also three rounds of interactions, through which the reenrollment of GTGP land increased by 4.8% and 3.2%, respectively. The dynamics in the land reenrollment converged when time = 11, where additional rounds of interactions among landholders did not affect the land reenrollment (Fig. 3). In addition, the effects of social norms were non-linear at different payment levels (Fig. 3). At a payment of 1,500 yuan per ha, 6.4 ha more GTGP land can be reenrolled if nine rounds of interactions among landholders were allowed. At a payment of 3,000 and 4,500 yuan per ha, nine rounds of interactions increased the GTGP reenrollment by 7.7 and 6.2 ha, respectively.
Fig. 3.
Simulated dynamics in the reenrollment of GTGP land due to the effects of social norms at different payments.
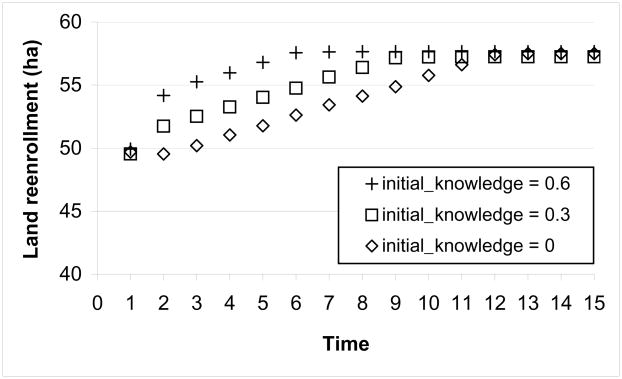
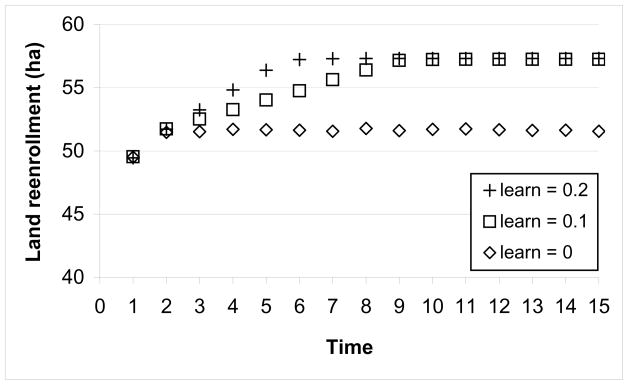
Dynamics in land reenrollment at a payment of 3,000 yuan per ha under different levels of initial_knowledge and learn are presented in Figure 4 and Figure 5. Higher levels of initial_knowledge resulted in higher land reenrollment before it converges (Fig. 4). For instance, the land reenrollment under initial_knowledge of 0, 0.3 and 0.6 when time = 5 was 51.8, 54.0 and 56.8 ha, respectively, and these changes were statistically significant (p-values < 0.001). Land reenrollment under different levels of initial_knowledge converged at about the same level (~ 57.5 ha), while land reenrollment under initial_knowledge of 0.6 converged the earliest (time = 9) and land reenrollment under initial_knowledge of 0 converged the latest (time = 14). By comparison, land reenrollment under learn of 0.1 and 0.2 converged at about the same level (~ 57.3 ha), although land reenrollment under learn of 0.2 converged at an earlier time than under learn of 0.1 (Fig. 5). However, land reenrollment under learn of 0 converged at a lower level (~ 51.6 ha). These results reflect the fact that as initial_knowledge and learn increase, landholders obtain more information on other landholders’ reenrollment decisions, which result in higher impacts of social norms on land reenrollment. A full knowledge’ (i.e. when knowledge = 1) can be obtained through multiple rounds of interactions as long as learn > 0, resulting in land reenrollment that converges to similar levels under different values for initial_knowledge and learn. When learn = 0, however, uncertainty in landholders’ perception of social norms cannot be reduced, and the effects of social norms remain at a lower level.
Fig. 4.
Simulated dynamics in the reenrollment of GTGP land due to the effects of social norms under different levels of initial_knowledge.
Fig. 5.
Simulated dynamics in the reenrollment of GTGP land due to the effects of social norms under different levels of learn.
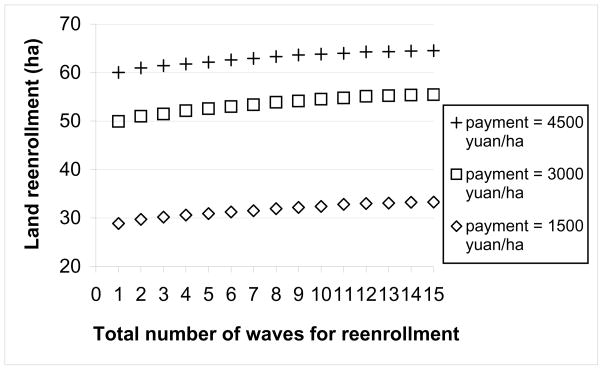
We also found more GTGP land can be reenrolled at the same payment due to the effects of social norms if households can be divided into multiple waves for reenrollment at different time (Fig. 6). For instance, at a payment of 3,000 yuan per ha, 5.3%, 9.2% and 11.0% more GTGP land can be reenrolled when households were divided into 5, 10 and 15 waves for reenrollment, and these increases were statistically significant (p-values < 0.001). The more waves the households were divided into, the more GTGP land can be reenrolled because households who made reenrollment decisions at a later time had more rounds of interactions with those who had already made reenrollment decisions, which resulted in larger normative effects by reducing uncertainties in their perceived social norms. In addition, the increment in the reenrollment of GTGP land due to additional division of households into waves was decreasing (Fig. 6). At a payment of 3,000 yuan per ha, a division of households into 5 waves for reenrollment increased land reenrollment by 5.3%, which was about 48.1% of the additional GTGP land that can be reenrolled when households were divided into 15 waves. The effects of social norms when households were divided into different waves for reenrollment were also non-linear at different payment levels (Fig. 6). For instance, when households were divided into 10 waves, 3.5, 4.6 and 3.8 ha more GTGP land can be reenrolled at payments of 1,500, 3,000 and 4,500 yuan per ha, respectively.
Fig. 6.
Simulated amount of GTGP land due to the effects of social norms when households were divided into different waves for reenrollment under different payments.
4. Discussion
Although previous studies have shown substantial impacts of social norms on the use of common-pool resources (Ostrom, 1990; 2000; Dietz et al., 2003) and other environmental behaviors (Cialdini, 2003; Goldstein et al., 2008; Nolan et al., 2008; Sidique et al., 2010), the evolution and impacts of social norms are context dependent (Dietz and Henry, 2008). In our case, only about 32.2% of households who participated in the GTGP would reconvert part or all of their GTGP plots to crop production after the payments ceased (Chen et al., 2009b), and most landholders would reenroll all of their GTGP plots in a new payment program even at a low payment. As a result, significant effects of social norms on the reenrollment of GTGP plots allowed more GTGP land to be reenrolled at the same payment. However, if circumstances were such that people generally do not support PES programs and social norms also play an important role in decision-making, then it is likely that the effects of social norms would increase the cost for land enrollment.
Our results showed that as the round of interactions among landholders increases, the increment in the reenrollment of GTGP land due to additional rounds of interactions was decreasing. Among all additional GTGP land that can be reenrolled due to 9 rounds of interactions, about half of them can be gained through the first three rounds of interactions. These results suggested that only a few rounds of interactions among landholders may be adequate to obtain most of the effects that social norms will have for land reenrollment. In addition, the effects of social norms were largest when the payment was intermediate, whereas the effects of social norms were smaller at higher and smaller payments. This was because higher payments induced higher levels of reenrollment, resulting in larger effects for social norms at intermediate payments than that at smaller payments. When the payment was much higher, most of GTGP land would be reenrolled even without considering the effects of social norms, and the additional reenrollment of GTGP land due to the effects of social norms will be smaller. Likewise, at very low payment levels few plots would be reenrolled, making any added effect of social norms small.
Since PES programs have usually been implemented for a duration of multiple years (up to 20 years or even longer, (OECD, 1997)), frequent interactions among landholders about their enrollment decisions may not be feasible, which makes diffusion of information on social norms difficult. In fact, previous studies found that diffusion of information about social norms played a key role for the effects of social norms to be incorporated into decision-making of stakeholders (Cialdini, 2003; Goldstein et al., 2008). We explored the effects of dividing households into multiple waves for reenrollment so that households who made reenrollment decision at a later time can perceive information on social norms through interactions with those who made reenrollment decision at earlier times. We found that more than 11% additional GTGP land can be reenrolled at the same payment by asking households to reenroll separately. Our results suggest that by changing policy arrangements and increasing stakeholders’ accessibility to information on other stakeholders’ responses to conservation investments, social norms can be used to improve the efficiency of PES programs and many other conservation investments around the world.
Agent-based models that include human agents often involve social learning. However, specific mechanisms of social learning can be complicated (Sobel, 2000). In some studies, agents may adopt the action of a randomly chosen agent (Fu et al., 2011) or actions of a group of other agents (Sobel, 2000; Satake et al., 2007) depending on the payoffs of their actions. In some other studies, individual agent’s decision may be determined by both its characteristics and other agents’ actions (Janssen and Ahn, 2006; Young, 2009). Based on the empirical data, we used both individual landholder’s characteristics and other landholders’ actions to determine the landholder’s action. However, information regarding landholders’ processes of learning about social norms was not available. Like many other studies (Satake et al., 2007; Fu et al., 2011), we conducted simulations at different values of parameters characterizing the learning process. Past studies also found substantial impacts of social networks on social learning (Franz and Nunn, 2009). Additional research on empirically measuring social learning processes and incorporating social networks into conservation investments is needed.
Acknowledgments
We thank Mingchong Liu, Weihong Tan, Shiqiang Zhou, Jinyan Huang, Jian Yang, Yingchun Tan, Xiaoping Zhou, Hemin Zhang of Wolong Nature Reserve, and Zhiyun Ouyang of the Chinese Academy of Sciences for their help during fieldwork. We thank William C. Clark and Paul R. Moorcroft of Harvard University and two anonymous reviewers for their constructive criticisms on an earlier draft of this paper. We gratefully acknowledge financial support from NSF, NASA, NIH, MSU Environmental Research Initiative, MSU Ag-Bio Research, and Giorgio Ruffolo Fellowship in Sustainability Science at Harvard University.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- An L, Linderman M, Qi J, Shortridge A, Liu J. Exploring complexity in a human-environment system: An agent-based spatial model for multidisciplinary and multiscale integration. Annals of the Association of American Geographers. 2005;95:54–79. [Google Scholar]
- An L, Lupi F, Liu J, Linderman MA, Huang J. Modeling the choice to switch from fuelwood to electricity Implications for giant panda habitat conservation. Ecological Economics. 2002;42:445–457. [Google Scholar]
- Bendor J, Swistak P. The evolution of norms. American Journal of Sociology. 2001;106:1493–1545. [Google Scholar]
- Carley K. Knowledge acquisition as a social phenomenon. Instructional Science. 1986;14:381–438. [Google Scholar]
- Case A. Neighborhood influence and technological change. Regional Science and Urban Economics. 1992;22:491–508. [Google Scholar]
- Chen XD, Lupi F, He GM, Liu JG. Linking social norms to efficient conservation investment in payments for ecosystem services. Proceedings of the National Academy of Sciences of the United States of America. 2009a;106:11812–11817. doi: 10.1073/pnas.0809980106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen XD, Lupi F, He GM, Ouyang ZY, Liu JG. Factors affecting land reconversion plans following a payment for ecosystem service program. Biological Conservation. 2009b;142:1740–1747. [Google Scholar]
- Chen XD, Lupi F, Vina A, He GM, Liu JG. Using cost-effective targeting to enhance the efficiency of conservation investments in payments for ecosystem services. Conservation Biology. 2010;24:1469–1478. doi: 10.1111/j.1523-1739.2010.01551.x. [DOI] [PubMed] [Google Scholar]
- Cialdini RB. Crafting normative messages to protect the environment. Current Directions in Psychological Science. 2003;12:105–109. [Google Scholar]
- Cialdini RB, Goldstein NJ. Social influence: Compliance and conformity. Annual Review of Psychology. 2004;55:591–621. doi: 10.1146/annurev.psych.55.090902.142015. [DOI] [PubMed] [Google Scholar]
- Cialdini RB, Reno RR, Kallgren CA. A focus theory of normative conduct: Recycling the concept of norms to reduce littering in public places. J Pers Soc Psychol. 1990;58:1015–1026. [Google Scholar]
- Coleman JS. Foundations of social theory. Harvard University Press; Cambridge, Mass: 1990. [Google Scholar]
- Deadman P, Robinson D, Moran E, Brondizio E. Colonist household decisionmaking and land-use change in the Amazon Rainforest: an agent-based simulation. Environment and Planning B-Planning & Design. 2004;31:693–709. [Google Scholar]
- Delong ER, Delong DM, Clarkepearson DI. Comparing the areas under 2 or more correlated receiver operating characteristic curves - a nonparametric approach. Biometrics. 1988;44:837–845. [PubMed] [Google Scholar]
- Dietz T, Henry AD. Context and the commons. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:13189–13190. doi: 10.1073/pnas.0806876105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dietz T, Ostrom E, Stern PC. The struggle to govern the commons. Science. 2003;302:1907–1912. doi: 10.1126/science.1091015. [DOI] [PubMed] [Google Scholar]
- Elster J. Social norms and economic theory. Journal of Economic Perspectives. 1989;3:99–117. [Google Scholar]
- Epstein JM. Learning to be thoughtless: Social norms and individual computation. Computational Economics. 2001;18:9–24. [Google Scholar]
- Fehr E, Gintis H. Human motivation and social cooperation: Experimental and analytical foundations. Annual Review of Sociology. 2007;33:43–64. [Google Scholar]
- Ferraro PJ, Simpson RD. The cost-effectiveness of conservation payments. Land Economics. 2002;78:339–353. [Google Scholar]
- Foster AD, Rosenzweig MR. Learning by doing and learning from others - Human-capital and technical change in agriculture. Journal of Political Economy. 1995;103:1176–1209. [Google Scholar]
- Franz M, Nunn CL. Network-based diffusion analysis: a new method for detecting social learning. Proceedings of the Royal Society B-Biological Sciences. 2009;276:1829–1836. doi: 10.1098/rspb.2008.1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu F, Rosenbloom DI, Wang L, Nowak MA. Imitation dynamics of vaccination behaviour on social networks. Proceedings of the Royal Society B-Biological Sciences. 2011;278:42–49. doi: 10.1098/rspb.2010.1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein NJ, Cialdini RB, Griskevicius V. A room with a viewpoint: Using social norms to motivate environmental conservation in hotels. Journal of Consumer Research. 2008;35:472–482. [Google Scholar]
- Gotts NM, Polhill JG. When and how to imitate your neighbours: Lessons from and for FEARLUS. Journal of Artificial Societies and Social Simulation. 2009:12. [Google Scholar]
- Grimm V, Berger U, Bastiansen F, Eliassen S, Ginot V, Giske J, Goss-Custard J, Grand T, Heinz SK, Huse G, Huth A, Jepsen JU, Jorgensen C, Mooij WM, Muller B, Pe’er G, Piou C, Railsback SF, Robbins AM, Robbins MM, Rossmanith E, Ruger N, Strand E, Souissi S, Stillman RA, Vabo R, Visser U, DeAngelis DL. A standard protocol for describing individual-based and agent-based models. Ecological Modelling. 2006;198:115–126. [Google Scholar]
- Grimm V, Berger U, DeAngelis DL, Polhill JG, Giske J, Railsback SF. The ODD protocol A review and first update. Ecological Modelling. 2010;221:2760–2768. [Google Scholar]
- Hanley JA, Mcneil BJ. The Meaning and Use of the Area under a Receiver Operating Characteristic (Roc) Curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- Jack BK, Kousky C, Sims KRE. Designing payments for ecosystem services: Lessons from previous experience with incentive-based mechanisms. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:9465–9470. doi: 10.1073/pnas.0705503104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James A, Gaston KJ, Balmford A. Can we afford to conserve biodiversity? Bioscience. 2001;51:43–52. [Google Scholar]
- James AN, Gaston KJ, Balmford A. Balancing the Earth’s accounts. Nature. 1999;401:323–324. doi: 10.1038/43774. [DOI] [PubMed] [Google Scholar]
- Janssen MA, Ahn TK. Learning, signaling, and social preferences in public-good games. Ecology and Society. 2006:11. [Google Scholar]
- Jaynes ET. Information Theory and Statistical Mechanics. The Physical Review. 1957;106:620–630. [Google Scholar]
- Li D, Bo F, Tao J. Achievements in and strategies for the Grain to Green Program in Hunan Province. Hunan Forestry Science & Technology. 2006;33:1–5. (in Chinese) [Google Scholar]
- Liang W, Bai C, Sun B, Hao D, Qi J. Soil moisture and physical properties of regions under Grain to Green Program in Gullied Rolling Loess Area. Soil and Water Conservation in China. 2006:17–18. (in Chinese) [Google Scholar]
- Liu F, Huang C, He T, Qian X, Liu Y, Luo H. Roles of Grain to Green Program in reducing loss of phosphorus from yellow soil in hilly areas. Journal of Soil Water Conservation. 2002;16:20–23. (in Chinese) [Google Scholar]
- Liu JG, Dietz T, Carpenter SR, Alberti M, Folke C, Moran E, Pell AN, Deadman P, Kratz T, Lubchenco J, Ostrom E, Ouyang Z, Provencher W, Redman CL, Schneider SH, Taylor WW. Complexity of coupled human and natural systems. Science. 2007;317:1513–1516. doi: 10.1126/science.1144004. [DOI] [PubMed] [Google Scholar]
- Liu JG, Li SX, Ouyang ZY, Tam C, Chen XD. Ecological and socioeconomic effects of China’s policies for ecosystem services. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:9477–9482. doi: 10.1073/pnas.0706436105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu JG, Linderman M, Ouyang ZY, An L, Yang J, Zhang HM. Ecological degradation in protected areas: The case of Wolong Nature Reserve for giant pandas. Science. 2001;292:98–101. doi: 10.1126/science.1058104. [DOI] [PubMed] [Google Scholar]
- Liu JG, Daily GC, Ehrlich PR, Luck GW. Effects of household dynamics on resource consumption and biodiversity. Nature. 2003;421:530–533. doi: 10.1038/nature01359. [DOI] [PubMed] [Google Scholar]
- Long HL, Heilig GK, Wang J, Li XB, Luo M, Wu XQ, Zhang M. Land use and soil erosion in the upper reaches of the Yangtze River: Some socio-economic considerations on China’s Grain-for-Green Programme. Land Degradation & Development. 2006;17:589–603. [Google Scholar]
- Louviere JJ, Hensher DA, Swait JD. Stated choice methods : analysis and applications. Cambridge University Press; Cambridge, U.K: 2000. [Google Scholar]
- Ma Y, Fan S. Ecological-economic effects of Grain to Green Program in desertification areas. Journal of Natural Resources. 2005;20:590–596. (in Chinese) [Google Scholar]
- Manski CF. Economic analysis of social interactions. Journal of Economic Perspectives. 2000;14:115–136. [Google Scholar]
- Matthews RB, Gilbert NG, Roach A, Polhill JG, Gotts NM. Agent-based land-use models: a review of applications. Landscape Ecology. 2007;22:1447–1459. [Google Scholar]
- Myers N, Mittermeier RA, Mittermeier CG, da Fonseca GAB, Kent J. Biodiversity hotspots for conservation priorities. Nature. 2000;403:853–858. doi: 10.1038/35002501. [DOI] [PubMed] [Google Scholar]
- Nolan JM, Schultz PW, Cialdini RB, Goldstein NJ, Griskevicius V. Normative social influence is underdetected. Personality and Social Psychology Bulletin. 2008;34:913–923. doi: 10.1177/0146167208316691. [DOI] [PubMed] [Google Scholar]
- OECD. The Environmental Effects of Agricultural Land Diversion Schemes. Organization for Economic Cooperation and Development (OECD); Paris: 1997. [Google Scholar]
- Ostrom E. Governing the Commons: The Evolution of Institutions for Collective Action. Cambridge University Press; New York: 1990. [Google Scholar]
- Ostrom E. Collective action and the evolution of social norms. Journal of Economic Perspectives. 2000;14:137–158. [Google Scholar]
- Parker DC, Manson SM, Janssen MA, Hoffmann MJ, Deadman P. Multi-agent systems for the simulation of land-use and land-cover change: A review. Annals of the Association of American Geographers. 2003;93:314–337. [Google Scholar]
- Phillips SJ, Anderson RP, Schapire RE. Maximum entropy modeling of species geographic distributions. Ecological Modelling. 2006;190:231–259. [Google Scholar]
- Satake A, Janssen MA, Levin SA, Iwasa Y. Synchronized deforestation induced by social learning under uncertainty of forest-use value. Ecological Economics. 2007;63:452–462. [Google Scholar]
- Sengupta R, Lant C, Kraft S, Beaulieu J, Peterson W, Loftus T. Modeling enrollment in the Conservation Reserve Program by using agents within spatial decision support systems: an example from southern Illinois. Environment and Planning B-Planning & Design. 2005;32:821–834. [Google Scholar]
- Sidique S, Lupi F, Joshi S. The effects of behaviors and attitudes on drop-off recycling activities. Resources, Conservation and Recycling. 2010;54:163–170. [Google Scholar]
- Siikamaki J, Layton DF. Potential cost-effectiveness of incentive payment programs for the protection of non-industrial private forests. Land Economics. 2007;83:539–560. [Google Scholar]
- Sobel J. Economists’ models of learning. Journal of Economic Theory. 2000;94:241–261. [Google Scholar]
- Vincent JR. Spatial dynamics, social norms, and the opportunity of the commons. Ecological Research. 2007;22:3–7. [Google Scholar]
- Wang Z, Wang X, Shi Y, Pan L, Yu X, Tang Z. Effects of Grain to Green Program on soil and water conservation in Zigui county of the Three Gorges Reservoir Region. Science of Soil and Water Conservation. 2007;5:68–72. (in Chinese) [Google Scholar]
- Wiley EO, McNyset KM, Peterson AT, CRR, Stewart AM. Niche modeling and geographic range predictions in the marine environment using a machine-learning algorithm. Oceanography. 2003;16:120–127. [Google Scholar]
- Wooldridge JM. Econometric Analysis of Cross Section and Panel Data. MIT Press; Cambridge, MA: 2002. p. 776. [Google Scholar]
- Wunder S. The efficiency of payments for environmental services in tropical conservation. Conservation Biology. 2007;21:48–58. doi: 10.1111/j.1523-1739.2006.00559.x. [DOI] [PubMed] [Google Scholar]
- Wunder S. Payments for environmental services and the poor: Concepts and preliminary evidence. Environment and Development Economics. 2008;13:279–297. [Google Scholar]
- Xu J, Yin R, Li Z, Liu C. China’s ecological rehabilitation: Unprecedented efforts, dramatic impacts, and requisite policies. Ecological Economics. 2006;57:595–607. [Google Scholar]
- Young HP. The economics of convention. Journal of Economic Perspectives. 1996;10:105–122. [Google Scholar]
- Young HP. Innovation Diffusion in Heterogeneous Populations: Contagion, Social Influence, and Social Learning. American Economic Review. 2009;99:1899–1924. [Google Scholar]