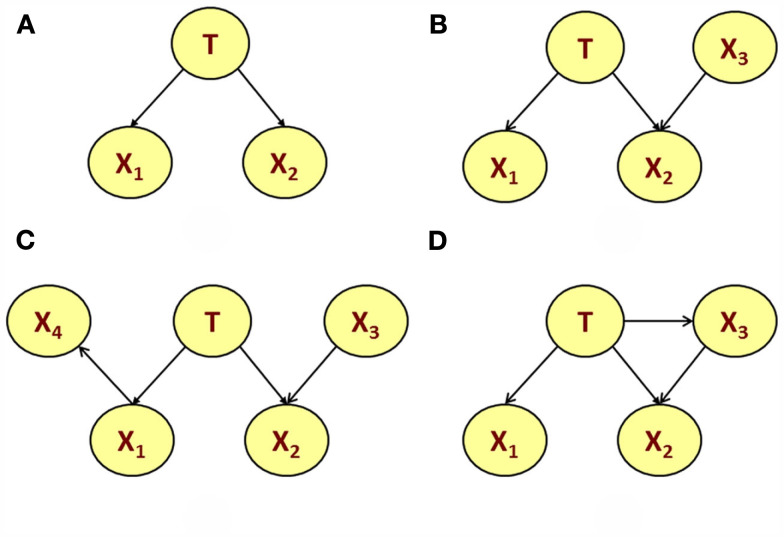
Figure 4.
Examples of directed acyclic graph (DAG). All nodes are random variables and the DAG represents Markov properties of marginal and conditional independence (Lauritzen and Sheehan, 2004). In particular, the global Markov property states that a node is independent of all other nodes in the DAG given its parent nodes, its children nodes and additional parents of its children (Lauritzen and Sheehan, 2004). In addition, two nodes are marginally independent when they have no directed joining paths after their children are dropped. Therefore, the nodes X1 and X2 in the DAG in (A) are conditionally independent given T. The DAG in (B) adds the node X3 to the NBC in (A). This additional node is marginally independent of T but conditionally dependent on T given X2. The DAG in (C) includes an additional node X4 that is conditionally independent of all other nodes given X1. Finally, the DAG in (D) extends the DAG in (B) by adding a link from T to X3 so that X3 and T are marginally dependent.