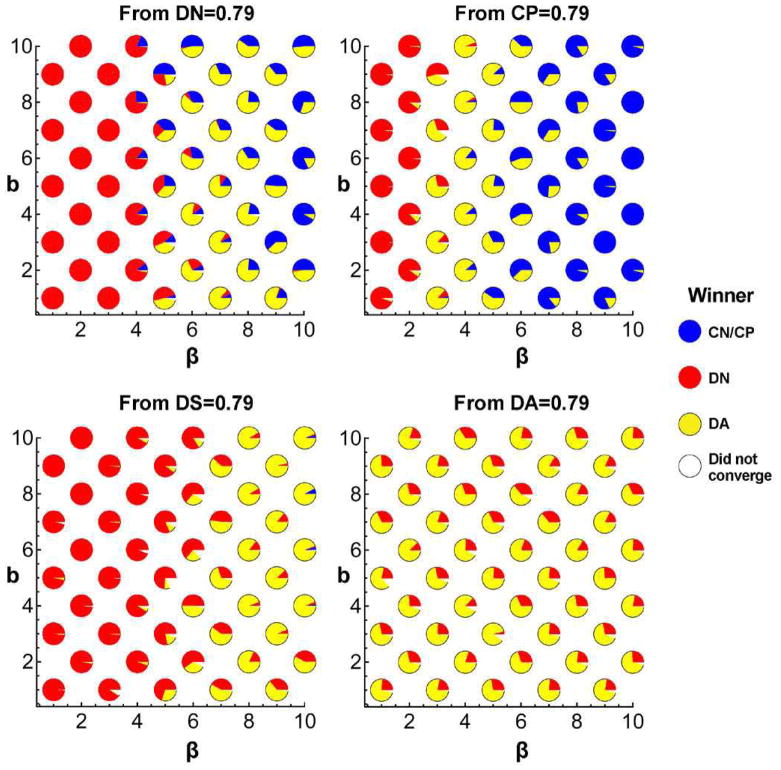
Figure 3.
Evolutionary outcomes of the full strategy set on a regular lattice. Cooperation cannot invade a population of antisocial defectors, DA. Starting from the specified initial condition, 50 agent based simulations are run and the winning strategy recorded. The blue portion of each circle indicates the fraction of runs where CP wins or CP, CN, CA and/or CS coexist; the red portion, the fraction of runs where DN wins; the yellow portion the fraction of runs where DA wins; the white portion, the fraction of runs in which there was no convergence after 125,000,000 generations. DP and DS never win. We consider small errors, ε = 0.01, and a 50 × 50 lattice for a total population size N = 2500. We use viability updating with parameter values γ = 0.1 and θ = 0.1. We explore the (b, β) parameter space, setting c = 1 and α = 1. Additional simulations find qualitatively similar results for α = 0.5 and α = 1.5. Initial population density (A) DN=0.79, all others 0.03 (B) CP=0.79, all others 0.03 (C) DS=0.79, all others 0.03 (D) DA=0.79, all others 0.03.