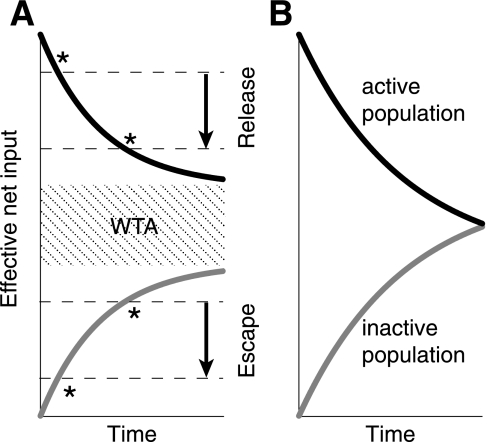
Fig. 5.

Dynamics of the mutual inhibition model can largely be characterized by tracking the net inputs to each population. Here we show a case where f(x) is a Heaviside function and only adaptation is considered (δ = 0). We set u₁ = 1 and u₂ = 0. Net input to population one is therefore α − γa₁ (t) + I. Net input to the inactive population is −β − γa₂(t) + I. A switch in activity occurs when either population crosses the firing rate threshold at zero. Alternatively, a switch in activity occurs when the “effective net input” [α −γa₁(t), black curve, active population, and −β − γa₂(t), grey curve, inactive population] crosses −I. Input I can therefore be thought of as setting the “effective threshold” of the firing rate function. Increasing I (black arrows) therefore decreases the effective threshold (dotted lines). Switches in activity occur when either curve crosses the −I threshold (events marked by *). A: when I is low, switches occur when the active population crosses threshold (release), and increases in I lead to longer time durations before a switch occurs (ID behavior). For intermediate I, neither population will cross threshold and WTA ensues. For larger I, switches occur when the inactive population crosses threshold, and increases in I lead to shorter durations before a switch occurs (DD behavior). B: parameters can be set such that WTA can never occur for any value of I.