Gay-Berne and electrostatic multipole based coarse-grain potential in implicit solvent

Abstract

A general, transferable coarse-grain (CG) framework based on the Gay-Berne potential and electrostatic point multipole expansion is presented for polypeptide simulations. The solvent effect is described by the Generalized Kirkwood theory. The CG model is calibrated using the results of all-atom simulations of model compounds in solution. Instead of matching the overall effective forces produced by atomic models, the fundamental intermolecular forces such as electrostatic, repulsion-dispersion, and solvation are represented explicitly at a CG level. We demonstrate that the CG alanine dipeptide model is able to reproduce quantitatively the conformational energy of all-atom force fields in both gas and solution phases, including the electrostatic and solvation components. Replica exchange molecular dynamics and microsecond dynamic simulations of polyalanine of 5 and 12 residues reveal that the CG polyalanines fold into “alpha helix” and “beta sheet” structures. The 5-residue polyalanine displays a substantial increase in the “beta strand” fraction relative to the 12-residue polyalanine. The detailed conformational distribution is compared with those reported from recent all-atom simulations and experiments. The results suggest that the new coarse-graining approach presented in this study has the potential to offer both accuracy and efficiency for biomolecular modeling.

INTRODUCTION

The ambition to understand molecular systems of increasing length and time scales drives the pursuit and development of coarse-grain (CG) computational models. It continues to be prohibitively expensive for all-atom molecular mechanics models to collect statistically converged measurements of molecular phenomena that involve large conformational rearrangements, such as protein folding, protein-protein interaction, and allosteric regulation.¹ Although there has been much development in the areas of enhanced sampling, the need to study the dynamics of large biomolecular systems over long time scales remains. Consequently, various coarse-graining strategies have been endeavored to model the systems of interest. Much effort has been made to develop coarse-grained models by matching the intermolecular interaction energy and force at the functional group or molecular level with all-atom simulations of specific systems. Klein and co-workers reported coarse-grained models of membrane lipids and proposed various coarse-graining strategies based on previous studies of polymer melts.^{2, 3} DeVane et al. have recently embarked on a method that employs the Lennard-Jones 9–6 and 12–4 forms to model nonbonded interactions of coarse-grain sites and have thus far validated the model on various amino acid side-chain analogs.⁴ Hills et al. has demonstrated that a physics-based, isotropic site, solvent-free method is able to maintain the native structures of Trpzip, Trp-cage, and the open/close conformations of adenylate kinase⁵ Moreover, the united-residue force field developed by Scheraga and co-workers has matured significantly and used to study the folding mechanism of specific domains of the staphylococcal protein A and the formin-binding protein.^{6, 7, 8, 9, 10, 11, 12, 13} Alternatively, sequence-based statistical potentials have been used as a coarse-grain approach to fold t-RNA, 5S, and 16S ribosomal RNA.^{14, 15}

In this work, a general coarse-grain model, consisting of rigid bodies of anisotropic Gay-Berne (GB) particles and point multipoles, has been developed. The Generalized Kirkwood method is applied to account for the solvation effects.¹⁶ While the current CG model is constructed from atomic force fields as with other coarse-grained models, our focus is on representing the general components of intermolecular forces such as electrostatic and repulsion-dispersion at a CG level, rather than matching the overall effective forces produced by atomic models. The strategy is much similar to that of developing empirical atomic potential energy model from quantum mechanical principles. The resulting CG model is transferable and not limited to specific systems or environments. Another distinct feature is that the model adopts the common functional forms that are supersets of all-atom model, which will facilitate future multi-scale applications.

MODEL AND METHODS

Gay-Berne potential

The coarse-grain repulsion-dispersion interactions are represented with anisotropic GB potentials. A full description of the Gay-Berne potential is available in our previous work^{17, 18} and in the supporting information as well. Based on Gaussian-overlap potential, the potential energy between two particles i and j has the form

$$U_{GB}({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\mathrm{r}}_{\mathit{ij}})=4\varepsilon ({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})\left[{\left(\frac{d_w{\sigma }_0}{{\mathrm{r}}_{\mathit{ij}}-\sigma ({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})+d_w{\sigma }_0}\right)}^{12}-{\left(\frac{d_w{\sigma }_0}{{\mathrm{r}}_{\mathit{ij}}-\sigma ({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})+d_w{\sigma }_0}\right)}^6\right],$$ (1)

where the range parameter $\sigma ({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})$ has the generalized form as

$$\sigma ({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})={\sigma }_0{\left[1-\left\{\frac{\chi {\alpha }^2{({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{r}}}_{\mathit{ij}})}^2+\chi {\alpha }^{-2}{({\widehat{\mathrm{u}}}_j·{\widehat{\mathrm{r}}}_{\mathit{ij}})}^2-2{\chi }^2({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{r}}}_{\mathit{ij}})({\widehat{\mathrm{u}}}_j·{\widehat{\mathrm{r}}}_{\mathit{ij}})({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{u}}}_j)}{1-{\chi }^2{({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{u}}}_j)}^2}\right\}\right]}^{-\frac{1}{2}},$$ (2)

and

$${\sigma }_0=\sqrt{d_i^2+d_j^2},$$ (3)

$$\chi ={\left[\frac{\left(l_i^2-d_i^2\right)\left(l_j^2-d_j^2\right)}{\left(l_j^2+d_i^2\right)\left(l_i^2+d_j^2\right)}\right]}^{1/2},$$ (4)

$${\alpha }^2={\left[\frac{\left(l_i^2-d_i^2\right)\left(l_j^2+d_i^2\right)}{\left(l_j^2-d_j^2\right)\left(l_i^2+d_j^2\right)}\right]}^{1/2},$$ (5)

where l and d are the length and breadth of each particle, respectively.

The terms χα², χα⁻², and χ² can be calculated as

$$\chi {\alpha }^2=\frac{l_i^2-d_i^2}{l_i^2+d_j^2},$$ (6)

$$\chi {\alpha }^{-2}=\frac{l_j^2-d_j^2}{l_j^2+d_i^2},$$ (7)

$${\chi }^2=\frac{\left(l_i^2-d_i^2\right)\left(l_j^2-d_j^2\right)}{\left(l_j^2+d_i^2\right)\left(l_i^2+d_j^2\right)}.$$ (8)

The total well-depth parameter is presented as

$$\varepsilon ({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})={\varepsilon }_0{\varepsilon }_1^{\nu }({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j){\varepsilon }_2^{\mu }({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}}).$$ (9)

The orientation-dependent strength terms are calculated in the following manner:

$${\varepsilon }_1({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j)={\left[1-{\chi }^2{({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{u}}}_j)}^2\right]}^{-1/2},$$ (10)

$${\varepsilon }_2({\widehat{\mathrm{u}}}_i,{\widehat{\mathrm{u}}}_j,{\widehat{\mathrm{r}}}_{\mathit{ij}})=1-\left\{\frac{{\chi }^{\prime }{\alpha }^{\prime 2}{({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{r}}}_{\mathit{ij}})}^2+{\chi }^{\prime }{\alpha }^{\prime -2}{({\widehat{\mathrm{u}}}_j·{\widehat{\mathrm{r}}}_{\mathit{ij}})}^2-2{\chi }^{\prime 2}({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{r}}}_{\mathit{ij}})({\widehat{\mathrm{u}}}_j·{\widehat{\mathrm{r}}}_{\mathit{ij}})({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{u}}}_j)}{1-{\chi }^{\prime 2}{({\widehat{\mathrm{u}}}_i·{\widehat{\mathrm{u}}}_j)}^2}\right\},$$ (11)

$${\chi }^{\prime }={\left[\frac{\left({\varepsilon }_{Si}^{1/\mu }-{\varepsilon }_{Ei}^{1/\mu }\right)\times \left({\varepsilon }_{Sj}^{1/\mu }-{\varepsilon }_{Ej}^{1/\mu }\right)}{\left({\varepsilon }_{Sj}^{1/\mu }+{\varepsilon }_{Ei}^{1/\mu }\right)\times \left({\varepsilon }_{Si}^{1/\mu }+{\varepsilon }_{Ej}^{1/\mu }\right)}\right]}^{1/2},$$ (12)

$${\alpha }^{\prime 2}={\left[\frac{\left({\varepsilon }_{Si}^{1/\mu }-{\varepsilon }_{Ei}^{1/\mu }\right)\times \left({\varepsilon }_{Sj}^{1/\mu }+{\varepsilon }_{Ei}^{1/\mu }\right)}{\left({\varepsilon }_{Sj}^{1/\mu }-{\varepsilon }_{Ej}^{1/\mu }\right)\times \left({\varepsilon }_{Si}^{1/\mu }+{\varepsilon }_{Ej}^{1/\mu }\right)}\right]}^{1/2}.$$ (13)

The well depth of the cross configuration is denoted by ɛ₀, the well depth of the end-to-end/face-to-face configuration is presented as ɛ_E, and ɛ_S denotes the well depth of the side-by-side configuration.¹⁹ Here we improved the accuracy of the Gay-Berne model by separating the ratio of ɛ_E/ɛ_S to two independent variables, ɛ_E and ɛ_S.

The new representations of χ^′ and α^′2 allow the consistent result for a pair of Gay-Berne particles of arbitrary types. Between unlike pairs, all ɛ₀ values and their ɛ_S and ɛ_E are specified explicitly or computed using a combining rule.²⁰ The d_W parameter describes the “softness” of the potential to allow better correlation with the all-atom energy profile. The parameters μ and ν were set to canonical values of 2.0 and 1.0, respectively. The current Gay-Berne potential with electrostatic multipole (GBEMP) model is implemented based on the TINKER molecular dynamics package.²¹

The terms χ^′2, χ^′α^′2, and χ^′α^′−2 were treated as inseparable and computed directly as

$${\chi }^{\prime 2}=\frac{\left({\varepsilon }_{Si}^{1/\mu }-{\varepsilon }_{Ei}^{1/\mu }\right)\times \left({\varepsilon }_{Sj}^{1/\mu }-{\varepsilon }_{Ej}^{1/\mu }\right)}{\left({\varepsilon }_{Sj}^{1/\mu }+{\varepsilon }_{Ei}^{1/\mu }\right)\times \left({\varepsilon }_{Si}^{1/\mu }+{\varepsilon }_{Ej}^{1/\mu }\right)},$$ (14)

$${\chi }^{\prime }{\alpha }^{\prime 2}=\frac{\left({\varepsilon }_{Si}^{1/\mu }-{\varepsilon }_{Ei}^{1/\mu }\right)}{\left({\varepsilon }_{Si}^{1/\mu }+{\varepsilon }_{Ej}^{1/\mu }\right)},$$ (15)

$${\chi }^{\prime }{\alpha }^{\prime -2}=\frac{\left({\varepsilon }_{Sj}^{1/\mu }-{\varepsilon }_{Ej}^{1/\mu }\right)}{\left({\varepsilon }_{Sj}^{1/\mu }+{\varepsilon }_{Ei}^{1/\mu }\right)}.$$ (16)

Electrostatic potentials are represented with pairwise interactions of point multipole sites up to quadrupole. Each rigid body may contain zero or more off-center multipole sites where the local frame of the site is aligned with the principal axis of the rigid body. A complete description of electrostatic interactions of the GBEMP model are provided in previous work.^{17, 18}

RESULTS AND DISCUSSION

Benzene and methanol model

The improved Gay-Berne functional form has been validated on benzene and methanol molecules, which were represented by disk-like and rod-like particles, respectively. As with the previous studies,^{17, 18} the Gay-Berne parameters were derived by first fitting to the gas-phase homodimer intermolecular interaction energy and then refined in the liquid simulations. All-atom homodimer interactions energy for cross, end-end, face-face, and side-by-side configurations was obtained at various separations up to 12 Å apart. At each separation, the dimer interaction energy was calculated as a Boltzmann average over configurations generated by rotation about the primary axis of each Gay-Berne particle. Molecular electrostatic multipole (EMP) moments of benzene and methanol in liquid environments were obtained from atomic multipoles, including induced dipoles, given by the all-atom AMOEBA polarizable force field.^{22, 23}

In coarse-grained liquid simulations, the initial structures of benzene and methanol particles were created by mapping from all-atom structures. After rigid-body energy minimization, MD simulations of a box of ∼300 molecules were performed with an NPT ensemble at 298 K and 1 atm. The periodic boundary condition was applied with a cutoff of 12 Å. Different time steps (up to 20 fs) were tested in the CG simulations.

A comparison of dimer interaction energies between the all-atom and GBEMP models shows that the new functions for combining the Gay-Berne well-depth parameters, ɛ_E and ɛ_S, produce a better agreement than the previous Gay-Berne function (see Table S1 of supplementary material).⁴⁹ The well-depth for benzene in the T shape configuration has increased to 0.91 Kcal/mol from 0.52 Kcal/mol (using the previous model) and more closely matches that of all-atom result (1.60 Kcal/mol) (see Figure S1).⁴⁹ Liquid simulations for benzene and methanol yield bulk properties, such as internal potential energy and density, which are in excellent agreement with the experimental values (error < 2%) (see Tables S2 and S3 of supplementary material).⁴⁹ More detailed comparison among CG and all-atom simulations, as well as experiment can be found in the supporting information. The GBEMP model is next extended to polyalanine peptides that consist of bonded coarse-grained particles.

Alanine model

In our CG model, a peptide is composed of covalently bonded rigid bodies, with Gay-Berne and/or electrostatic multipole sites. Bonding occurs between the Gay-Berne or EMP sites on different rigid bodies. Bond stretch energies adopt the fourth-order Taylor expansion of the Morse potential. Bond angle bend energies utilize a sixth-order potential. A three-term Fourier series expansion is calculated with the torsion energy. These valence functional forms are similar to those used by classical molecular mechanics potential such as MM3.²⁴ To use large time-step in MD simulations, the bond and angle terms can be restrained using rattle algorithm.²⁵

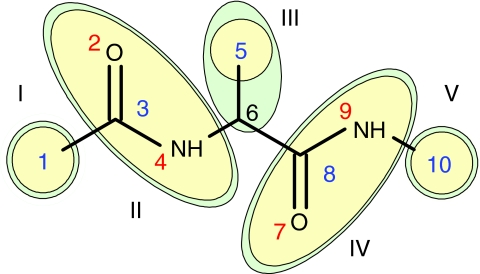
In a previous work,¹⁸ we have devised a general rigid-body representation containing an arbitrary number of off-centered Gay-Berne and multipole interaction sites that share the same local frame. Gay-Berne interactions are computed using orientation and site location vectors in Cartesian coordinates, relative to the local frame of the rigid body, as variables. Likewise, multipole interactions are computed via positions given by Cartesian coordinates relative to the local frame of the rigid body. The dialanine model consists of five rigid bodies (I through V) as depicted in Fig. 1. Gay-Berne parameters of amide and methyl groups were obtained with the same procedure as described above, by fitting to AMOEBA atomic force field. As in Fig. 1, the rigid body that represents the amide group consists of one Gay-Berne particle and two EMP sites. Gay-Berne sites 1, 5, and 10 are spherical methyl groups while sites 3 and 8 are equivalent ellipsoid amide groups. Similarly, sites 2 and 7 share the same EMP type, as do sites 4 and 9. Site 6 is used to compute bonded interactions only. Bonds exist between sites (1, 3), (4, 6), (6, 8), and (9, 10). An example of an angle is composed of sites (1, 3, and 2) and a torsion angle is composed of sites (3, 4, 6, and 8). The 12-mer alanine model polymerizes rigid bodies II and III from Fig. 1 as a repeating unit 12 times, thus, requiring 27 rigid bodies. For each rigid body type, the coordinates of the corresponding atoms are recorded in the local frame, which allow us to map the coarse grain molecules back to all-atom structures. Note that although the Gay-Berne particle is symmetric about the primary axis, the rigid body is not necessarily symmetric due to the presence of off-center site and/or multipoles.

Figure 1.

Representation of dialanine GBEMP model. Ellipsoids encompass the rigid bodies (green) that contain Gay-Berne (blue) and multipole (red) interaction sites. The Gay-Berne particles are located at the center of the mass of the corresponding atoms.

Solvation is represented implicitly and is composed of polar and nonpolar contributions. Polar solvation employs the Generalized Kirkwood (GK) method,¹⁶ a multipolar extension of the Generalized Born approach^{26, 27} and is computed for all the multipole sites. The Grycuk effective radius²⁸ is used in the polar solvation calculations. Nonpolar solvation is evaluated for all Gay-Berne sites with the ACE surface area method²⁹ and Still method^{26, 30} to estimate the effective radius of each particle. All solvation methods as well as effective radii estimation methods are implemented in the TINKER 5 (Ref. ²¹) molecular modeling package and adapted to the current GBEMP suite. Particle radii used for effective radii estimation are taken from the maximum of the Gay-Berne l or d parameters. Rigid bodies with more than one multipole site, like the amide groups in Fig. 1 (II and IV), uniformly divide the Gay-Berne radius value among all sites.

Parameters for the alanine model were obtained for the non-bonded terms, such as Gay-Berne and electrostatic multipole potentials, as well as the bonded terms, such as bond stretching, angle bending, and torsion energies. Applying the same procedure used to parameterize benzene and methanol, Gay-Berne and EMP parameters for each rigid body in an alanine residue were fit to all-atom homodimer energy and monomer multipole (in solution environments), respectively. Bond stretch and angle bend parameters were parameterized via Boltzmann inversion with atomic configurations generated from molecular dynamics of alanine dipeptide using AMOEBA. Molecular dynamics were executed in an NVT ensemble with explicit solvent (209 water molecules) in a 19.7 Å box with a 1 fs time step at 298 K. Torsional energy parameters were fit to the all-atom conformational energy map generated with fixed-charge OPLSAA with Generalized Born Surface Area implicit solvation.^{26, 29} OPLSAA is chosen as it is a commonly used atomic force field and uses the similar torsional energy function as in the current coarse-grain model. Nonetheless, the torsional parameters will be refined in the future by comparing directly to experimental data.³¹ As we discuss below, the torsional term only contributes to a fraction of the conformational energy along with the intramolecular nonbonded electrostatic and van der Waals (vdW) interactions.

Dialanine energy components from coarse-grain model

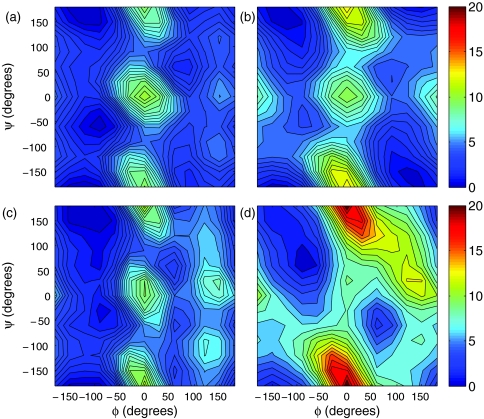
The conformational energy of dialanine as a function of backbone dihedral angles, ϕ and ψ, is investigated in solution and gas phases. Conformations are generated at 30° intervals starting at the origin of the energy map by minimization with restraints. Conformational energies for the GBEMP model in solution- and gas-phase are shown in Fig. 2, compared with corresponding energies from all-atom model using the OPLSAA field.³² The energy surface of the GBEMP model is smoother than that of the all-atom model as a consequence of coarse-graining. Nonetheless, the overall features of the CG gas phase energy maps are in fair agreement with the corresponding map of the atomic OPLSAA force field. Moreover, solution phase energy maps are in excellent qualitative agreement between the GBEMP and atomic force field. The agreement between solution phase energy maps is better than that of the gas phase maps and is expected since both are designed to describe solution phase properties. This is encouraging as the CG torsional parameters were only fit to the OPLSAA energy in solution. In addition, the solution-phase minima for alpha-helix, beta-sheet, as well as the less stable left-handed alpha-helix conformations are well manifested in the energy map.

Figure 2.

Total conformational energy (kcal/mol) of alanine dipeptide: (a) CG model in solution, (b) CG model in gas-phase, (c) all-atom model (OPLSAA) in solution, (d) all-atom model (OPLSAA) in gas-phase.

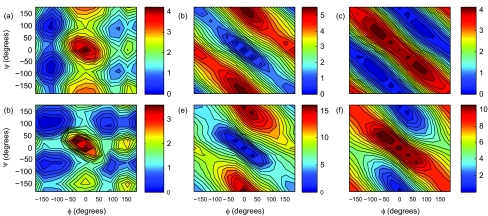
When compared to the gas-phase electrostatic energy (Figs. 3b, 3e), the solvation energy contribution (Figs. 3c, 3f) clearly compensates the electrostatic interactions in gas-phase. This observation, true for both all-atom (OPLSAA) and the current CG potentials, is consistent with the physical interpretation that when secondary structure forms, intramolecular hydrogen bonds replace the hydrogen bonds between peptide and surrounding water.

Figure 3.

Decomposition of alanine dipeptide energy (kcal/mol). Coarse-grain: (a) Gay-Berne energy, (b) gas-phase electrostatic energy, and (c) implicit solvation energy from GK/SA. All-atom: (d) vdW energy, (e) gas-phase electrostatic energy, and (f) implicit solvation energy from GB/SA.

We further compared the energy components of the coarse-grained GBEMP model with OPLSAA. A decomposition of the non-bonded interactions indicates that steric interaction given by the Gay-Berne function in the GBEMP model resemble that given the atomic vdW interaction energy of the OPLSAA force field over the Ramachandran map (Figs. 3a, 3d), including the scale. Likewise, contour maps of the gas-phase electrostatic energy (Figs. 3b, 3e), as well as the implicit solvation energy (Figs. 3c, 3f), show good agreement between the coarse grain and the all-atom results. Although the overall scales are different, the two components seem to mostly cancel each other as discussed above. As a result, the total energy minimum at the alpha-helix conformation mostly arises from the vdW contribution (Figs. 3a, 3d). A comparison of the torsional energy contribution (supporting information) between the CG and all-atom models also expresses a consistent behavior. The gas-phase conformational energy captures the C5 local minimum well.³³ However, the C7eq and C7ax minima have drifted slightly from the all-atom conformations. This may be due to the torsional energy contributions since their parameters were fit to the condensed-phase energy map. However, as with other all-atom fixed-charge models, transferability between gas- and solution-phase requires the inclusion of polarization effect.

Simulation of polyalanine

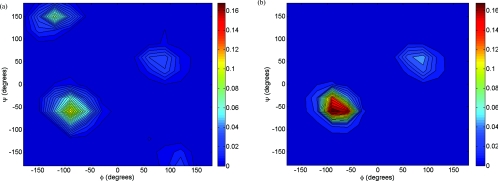
The conformation of polyalanine with various lengths has been investigated with both experimental and computational approaches.^{31, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47} To compare the GBEMP model with experiments and all-atom MD simulations, we investigated the blocked 5-mer polyalanine using GBEMP model in MD simulations. The aforementioned Generalized Kirkwood implicit solvent was utilized. The replica exchange molecular dynamics (REMD)⁴⁸ was performed to elucidate the conformational distribution of the 5-mer polyalanine. Thirty replicas were used between 298 and 800 K and the simulation time for each replica was 200 ns. The distribution of ϕ and ψ angles for all residues is shown in (Fig. 4a). Three dominant populations were observed: alpha-helix (−160° ⩽ ϕ ⩽ −20° and −120° ⩽ ψ ⩽ 50°), beta-strand (−180° ⩽ ϕ ⩽ −90° and 50° ⩽ ψ ⩽ 240°; or 160° ⩽ ϕ ⩽ 180° and 110° ⩽ ψ ⩽ 180°), and left-handed helix (20° ⩽ ϕ ⩽ 160° and −50° ⩽ ψ ⩽ 120°). The 5-mer polyalanine conformations observed are comparable with all atom simulation results (Table 1). Although circular dichroism (CD) spectroscopy and Fourier-transform infrared (FTIR) experiments reported somewhat less alpha-helix conformation,⁴⁷ the distributions sampled from MD simulations using all-atom force fields seem to be in qualitative agreement with what we obtained from the GBEMP simulations. Moreover, since the GBEMP model was developed based on interactions of all-atom force fields, it is reasonable for the model to behave consistently with all-atom simulation. Additionally, the population of full alpha-helices, in which ϕ and ψ angles of all five residues adopt the alpha-helical conformation, occurs at 4.62%, in comparison with 8% and 1% observed in all-atom simulations using CHARMM and Amber03 force field, respectively.⁴⁷

Figure 4.

Conformational distribution of 5-mer (a) and 12-mer (b) polyalanine from CG REMD simulations.

Table 1.

Per-residue fractions of 5-mer polyalanine from experiments and all-atom simulations.

Conformation	CD1	FTIR1	All-atom1 2, 1n2	CHARMM 27/cmap2	OPLSAA/L2	GBEMP
Alpha-helix	13 ± 3%	13 ± 5%	4%–60%1	57.5%	32.8%	46%
Beta-strand	N/A	N/A	9.8%–55.5%1	19.8%	32.0%	28%

¹Distributions from experiment and various force fields (see Ref. 47).

²Distributions of various force fields (see Ref. 31).

To study the effects of chain-length, a 12-residue polyalanine system was simulated using REMD with 30 replicas and 500 ns for each replica. Residue-level fractions observed were 42%, 4.3%, and 21% for alpha-helix, beta-strand, and left-handed helix conformations, respectively. Although the beta-strand conformation exhibits a minima in the conformational energy landscape (Figs. 2a, 2c), a substantial (5-fold) decrease in the beta-strand fraction compared to the 5-mer polyalanine suggests that the hydrogen bonding scheme provided by the alpha-helix conformation stabilizes the 12-mer polyalanine. Additionally, simulated annealing MD simulations were performed to inspect the minimum-energy structure of the peptide after an initial rigid-body energy minimization. The systems were heated to 1000 K within the first 50 ps and then cooled linearly to less than 1 K over 60 ns. Five independent simulated annealing trials were performed and an example of the final structure is shown in Figure S5 of supplementary material.⁴⁹ The final polyalanine structures after simulated annealing all adopt the alpha-helical conformation at low temperatures (100 K, see Figure S3 of supplementary material).⁴⁹ A comparison of the RMSD between structures obtained from the simulated annealing trajectory and a canonical alpha-helix (see Figure S5 of supplementary material)⁴⁹ suggests that the accessible area of phase-space noticeably increases as the temperature rises above 500 K.

Furthermore, MD simulations of a few microseconds were performed at room temperature to verify the convergence of the conformational space determined by the GBEMP/REMD. These simulations started with different initial structures, including the extended conformation, alpha-helix, and partial alpha-helical and beta-strand conformations. The torsional distribution sampled from the GB-EMP MD simulation (6 μs for 12-mer and 2 μs for 5-mer) at 298 K is in agreement with the REMD conformational map and is provided in the supplementary material (Figure S6).

Computational efficiency of the Gay-Berne potential with electrostatic multipole model

The GBEMP model provides a great improvement in the performance of molecular modeling. Due to the reduction of particle numbers and larger time-steps, the computational efficiency is enhanced by a factor of 50–800 compared to all-atom models tested with implicit and explicit solvent in this study (see Table S2 in the supplementary material).⁴⁹ Furthermore, the absence of high frequency motions, as required by all-atom models, allows time steps of up to 5 fs in MD simulations. Therefore, the CG model can achieve an improvement of about three orders of magnitude in the simulation speed and enable studies of large systems or extended simulation times from nanoseconds to microseconds.

CONCLUSIONS

A unique coarse-grained GBEMP (Gay-Berne potential with electrostatic multipole) model has been developed based on the general physical principles of molecular interactions. In this CG potential, the fundamental components of intermolecular forces are represented explicitly: the van der Waals interaction is described by treating molecules as soft uniaxial ellipsoids interacting via a generalized anisotropic Gay-Berne function; the charge distribution is represented by off-center multipoles, including point charge, dipole, and quadrupole moments. The Generalized Kirkwood method and the ACE surface area method are used to calculate the polar and nonpolar solvation energy, respectively.^{16, 29} The coarse-grained GBEMP model has been implemented in the TINKER modeling package capable of rigid-body molecular dynamics simulation. The replica-exchange method is implemented to enhance sampling. The CG parameters are calibrated using all-atom force field (AMOEBA and OPLS-AA) and extension to other molecular systems is straightforward. Most importantly, there is no need for constant re-parameterization when applied to different environments. We tested the CG model on the alanine peptides of various lengths. The results show that the model and parameters can be directly transferred from gas phase to solution (with implicit solvent model), and from dialanine to polyalanine of different lengths. For the first time, we show that the individual energy components in the coarse-grained model, including vdW, electrostatics, solvation, and torsional energy contributions, match closely with those of all-atom force fields, in both gas-phase and solution. REMD and room-temperature MD simulations of 5-residue and 12-residue polyalanines predict reasonable alpha-helix and beta-sheet populations in comparison with all-atom simulations and experiments. Due to the reduction of particle numbers and larger time-steps, the computational efficiency is enhanced by a factor of up to 1000 compared with all-atom simulations. Further speedup is possible if the bonds and angles are restrained. The coarse-graining potential presented in this study can be extended to various biomolecular systems and even combined with all-atom potential in multiscale applications.