Quantitative Trait Locus Mapping of Yield-Related Components and Oligogenic Control of the Cap Color of the Button Mushroom, Agaricus bisporus

Abstract

As in other crops, yield is an important trait to be selected for in edible mushrooms, but its inheritance is poorly understood. Therefore, we have investigated the complex genetic architecture of yield-related traits in Agaricus bisporus through the mapping of quantitative trait loci (QTL), using second-generation hybrid progeny derived from a cross between a wild strain and a commercial cultivar. Yield, average weight per mushroom, number of fruiting bodies per m², earliness, and cap color were evaluated in two independent experiments. A total of 23 QTL were detected for 7 yield-related traits. These QTL together explained between 21% (two-flushes yield) and 59% (earliness) of the phenotypic variation. Fifteen QTL (65%) were consistent between the two experiments. Four regions underlying significant QTL controlling yield, average weight, and number were detected on linkage groups II, III, IV, and X, suggesting a pleiotropic effect or tight linkage. Up to six QTL were identified for earliness. The PPC1 locus, together with two additional genomic regions, explained up to 90% of the phenotypic variation of the cap color. Alleles from the wild parent showed beneficial effects for some yield traits, suggesting that the wild germ plasm is a valuable source of variation for several agronomic traits. Our results constitute a key step toward marker-assisted selection and provide a solid foundation to go further into the biological mechanisms controlling productive traits in the button mushroom.

INTRODUCTION

Many economically important production traits in mushroom cultures, such as yield, quality, and resistance to diseases, are under polygenic inheritance (7, 26, 30, 31). Classical breeding and selection for such traits rely on phenotypic assessment and complex statistically based biometrical methods (6). Although these methodologies have been proven to be effective (23, 27), they have shown some limits. Indeed, these quantitative genetic approaches are based on a global analysis of phenotypic-trait variation through variance components, heritabilities, and least number of effective factors, but the individual genetic effects of these factors remained inaccessible. The development of molecular markers and linkage maps provides efficient tools to dissect complex inherited traits through analysis of quantitative trait loci (QTL). The use of these data in combination with whole-genome sequences also opens new opportunities for understanding the molecular and physiological bases of the traits studied.

Gene and QTL mapping have been developed more recently in fungi than in plant or animal species. If numerous QTL analyses related to life history traits have been reported for various fungi (4, 17–19, 34), those concerning yield-related traits in edible mushrooms are scarcer. In the oyster mushroom, Pleurotus oestratus, QTL controlling the growth rate, biomass production, and several production traits have been described (15, 16, 29). Although the button mushroom, Agaricus bisporus (Lange) Imbach, is the most widely cultivated edible mushroom species in Europe and North America (28), little is known about the genetic bases of important agronomic traits. Quantitative trait loci involved in disease resistance have been reported (22, 30), but to our knowledge, no QTL related to yield or quality components have yet been published. More than 90% of the A. bisporus mushrooms cultivated in the world have a white pileus color, in line with consumer preferences. For this important quality trait, a locus (PPC1) had been identified and related to DNA markers (3, 20), but our own observations during breeding programs showed that secondary loci may be involved in fine regulation of the cap color. The recent development of a comprehensive linkage map of A. bisporus (8) makes it possible to investigate the inheritance of complex traits in the species through QTL analyses.

The aim of this study was to identify and locate QTL involved in the genetic control of several yield-related traits and cap color parameters in second-generation hybrid progeny derived from a cross between a wild strain (JB3; A. bisporus var. burnetti) and a commercial cultivar (U1; A. bisporus var. bisporus). Prospects for the use of molecular markers in breeding of the button mushroom are discussed. A companion paper (8a) completes the drawing of the genetic architecture of major agronomic traits in A. bisporus by reporting the results of QTL analysis for partial resistance to Lecanicillium fungicola, responsible for the dry-bubble disease, one of the most detrimental disorders in mushroom crops.

MATERIALS AND METHODS

A. bisporus strains.

The population used in our study consisted of 89 second-generation hybrids obtained by crossing the homokaryotic offspring (H_i) of the hybrid JB3-83 × U1-7 with the homokaryon U1-2 (3, 10). The parental strains JB3 (wild isolate; ATCC 200853; ARP Collection) and U1 (commercial strain; Somycel, Langeais, France), the first-generation hybrid JB3-83 × U1-7 (11), and three commercial cultivars (Amycel 2100, Euromycel 25, and Euromycel 48) were used as controls in the experiments.

Experiment design and phenotypic evaluation.

Two independent fruiting trials (H0513 and H0517) were carried out at Centre Technique du Champignon (CTC) facilities (Distré, France) in two growing rooms with controlled environments (temperature, air speed, and humidity). H0513 started in April 2005 and H0517 1 month later. Mushrooms were grown on commercial mushroom compost, spawned at 0.8% in 0.09-m² trays filled with 9 kg of compost. Incubation was at 24°C for 13 days before a conventional casing layer was applied at the surface of the compost. Nine days after casing, fruiting was induced at 16°C and 95 to 98% relative humidity. In each experiment, one replicate, equivalent to one tray, of each strain was evaluated in a complete randomized design with two blocks. The agronomic traits studied are described in Table 1. Mushrooms were picked at developmental stage 3 according to the method of Hammond and Nichols (9), with a closed veil. Harvest was done daily over 5 weeks. Per tray, the total weight of all harvested mushrooms (cap and stipe) and their number (n) were recorded and normalized per surface unit (m²) to obtain the yield (Y = weight/0.09) and the number of fruiting bodies per surface unit (N = n/0.09). The average weight (W) was calculated as follows: W = weight/n. The data were analyzed for midproduction (2F, cumulative data for the first two flushes) and the end of the crop (E, cumulative data for the whole cropping period). The earliness (J1) was defined as the time, in days, from casing until the first harvest (7). The cap surface color was assessed for the first two flushes according to the method of Rodier et al. (27) with the tristimulus CIELAB coordinates (L, a, and b). The measures were performed immediately after harvest using a Minolta Chromameter (CR-300). For statistical analyses, the lightness, L, was transformed in logit scale, as recommended by Moquet et al. (24), as follows: logitL = log[L/(100 − L)].

Table 1.

Variation of yield-related traits and color parameters for the two experiments^a

Trait	Definition	Code	Expt H0513				Expt H0517				Pearson correlation coefficientd	Spearman rank correlation coefficientd	Best 20 hybrids concordance (%)
			Parental lines			Hybrids {mean (SD) [min-max]}	Parental lines			Hybrids {mean (SD) [min-max]}
			JB3	U1	H		JB3	U1	H
Yield-related traits
No. of fruiting bodies	No. of mushrooms per surface unit (no./m2)
Cumulative data for the first two flushes		N2F	4,500	2,222b	3,683	2,112 (651) [417c–3,772]	3,555	1,728b	3,377	1,992 (619) [539–3,450]	0.69	0.46	70
Cumulative data for the whole cropping period		NE	6,672	2,455b	5,539	2,861 (872) [567c–5,389]	5,111	1,978b	4,922	2,896 (849) [738–5,216]	0.77	0.57	65
Mushroom wt	Avg wt of mushrooms (g/mushroom)
Cumulative data for the first two flushes		W2F	5.48	10.11	6.91	11.52 (2.21) [7.8–18.02c]	7.52	11.09	7.31	11.44 (1.86) [7.28–17.49c]	0.64	0.42	65
Cumulative data for the whole cropping period		WE	5.36	9.87	6.64	11.26 (1.94) [7.56–17.11c]	6.75	10.94	6.98	10.89 (1.63) [6.84–16.71c]	0.75	0.5	65
Yield	Wt of fruiting bodies harvested per surface unit (kg/m2)
Cumulative data for the first two flushes		Y2F	24.34	22.46	25.44	22.94 (4.9) [7.26c–34.8c]	26.73	19.12	24.77	21.65 (4.5) [8.65c–32.31]	0.70	0.45	60
Cumulative data for the whole cropping period		YE	34.93	24.2	36.72	30.62 (6.43) [9.69c–41.75]	33.94	21.32	34.2	30.17 (5.88) [12.15–40.5]	0.75	0.48	75
Earliness	Time (in days) from casing until harvest of the first fruiting bodies	J1	18	23	19	19.69 (1.68) [16–24]	18	21	19	18.62 (1.77) [14.5–22]	0.76	0.55	50
Color parameters
Lightness	L; coordinate from CIELAB system
Avg of 10 mushrooms per genotype for the first flush		LF1	60.47	91.37b	63.92	77.36 (12.35) [55.36–91.52]	57.56	91.81b	64.53	77.52 (13.28) [54.13–92.9]	0.99	0.75	80
Avg of 10 mushrooms per genotype for the second flush		LF2	60.52	91.43b	66.21	78.5 (14) [55.07–91.52]	60.09	91.02b	68.9	78.6 (20.1) [56.56–92.94]	0.96	0.69	70
Green-red chromaticity component	a; coordinate from CIELAB system
Avg of 10 mushrooms per genotype for the first flush		aF1	10.18	0.57b	9.14	4.41 (3.66) [0.06–10.42]	9.74	−0.18b	9.00	4.29 (3.91) [−0.52–10.4]	0.99	0.9	55
Avg of 10 mushrooms per genotype for the second flush		aF2	9.85	−0.07b	7.82	3.82 (3.34) [−0.4–9.91]	8.86	−0.24b	7.41	3.75 (3.47) [−0.61–9.73]	0.96	0.83	80
Blue-yellow chromaticity component	b; coordinate from CIELAB system
Avg of 10 mushrooms per genotype for the first flush		bF1	23.45	10.02b	24.39	17.14 (6.11) [9.08–25.14]	21.94	9.46b	24.91	17.52 (6.02) [8.64–25.64]	0.98	0.87	65
Avg of 10 mushrooms per genotype for the second flush		bF2	23.31	9.61b	23.29	16.9 (5.84) [9.06–25]	20.73	10.53b	23.39	16.65 (6.55) [8.06–25.21]	0.97	0.77	70

^aEach trait is defined and encoded. For each experiment, the average values for parental lines JB3, U1, and H (JB3-83 × U1-7) are detailed, and the variation among the second generation of hybrids (H_i × U1-2) is described as follows: mean (standard deviation) [range of variation]. The coefficient of variation (CV), expressed as a percentage, and the broad-sense heritabilities are indicated. Between the two experiments and for each variable, Pearson's correlation coefficient is given.

^bSignificant difference between U1 and JB3 (SNK tests; P < 0.05).

^cSignificant transgressive genotype(s) detected among the hybrids (SNK test; P < 0.05).

^dAll the correlation coefficients are significant (P < 0.001).

Statistical analyses.

Data from the two independent experiments were initially combined to perform analyses of variance (ANOVA) according to the following model: Y = μ + G + E + G × E + B(E) + ε, where G was the genotypic effect, E was the experiment effect, G × E was the experiment times the genotype interaction, B(E) was the nested block within the experiment effect, and ε was the residual effect.

Data were also analyzed for each trait in each experiment independently according to the following model: Y = μ + G + B + ε, where G and B are the genotypic effect and the block effect, respectively. For each trait, hybrids were declared transgressive when their values differed from either the highest or the lowest parental value due to the post hoc Student-Newman-Keuls (SNK) test (P < 0.05). A comparison of the hybrids' ranking between the two experiments was performed with Spearman rank correlation coefficients (r_s). The percentage of hybrids matching in the 20 highest-performing genotypes defined statistically in both experiments was calculated.

Broad-sense heritabilities (h²) based on genotypic mean values were estimated as follows: h² = σG2/[σG2 + (σe2/n)] for each experiment and σG2/[σG2 + (σG × E2/rn) + (σe2/n)] for the combined data, where σG2 represented the genetic variance, σG × E2 the variance of genotype-experiment interaction, σe2 the environmental variance, n the num-ber of replicates within the experiment, and r the number of experi-ments.

Phenotypic correlations between pairs of traits within an experiment and for one trait between experiments were calculated using the Pearson coefficient r_p.

Data analyses were performed with the R open-source software.

QTL detection.

The genetic linkage map used for QTL mapping was previously developed by Foulongne-Oriol et al. (8). A framework was established with a subset of 217 markers well distributed over the genome.

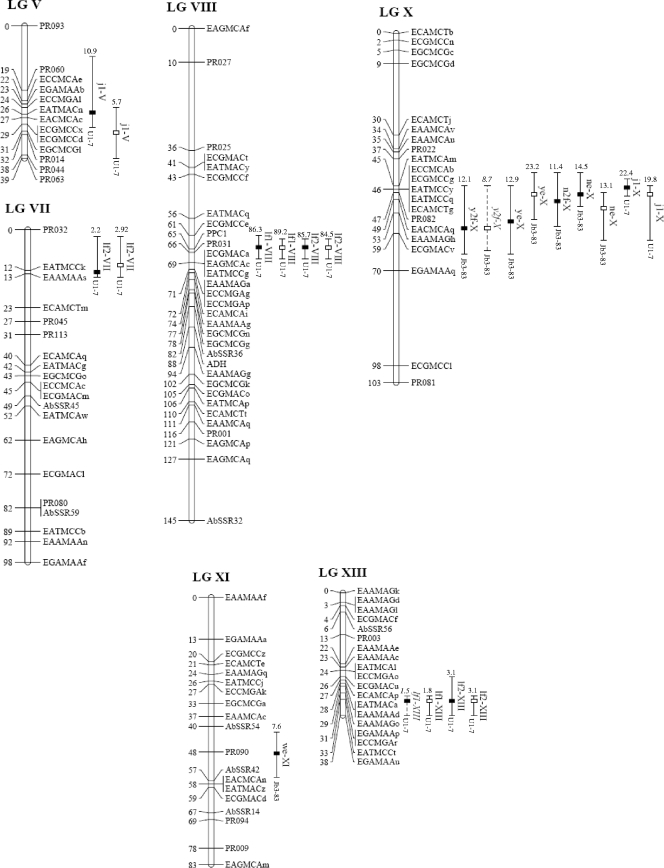
QTL detection was performed by linear regression (LR), interval mapping (IM), and composite interval mapping (CIM) with QTL Cartographer software (1), using B1 design. For each trait, a 1,000-permutation test was performed to estimate the appropriate significant threshold for LR, using an experimentwise error (α) of 0.05. This threshold was chosen for QTL detection with IM and CIM models. Up to five markers showing the highest F statistics after the forward-backward stepwise regression analysis were added as cofactors in the CIM step (model 6, using a moving-window size of 10 centimorgan [cM] and a walking speed of 2 cM). The most likely position of the QTL was estimated by the point where the maximum logarithm of the odds (LOD) score was found. The confidence interval (CI) was defined as the map interval corresponding to a 1-LOD decrease on either side of the LOD peak. QTL detected for several traits and/or for the two experiments were considered to be the same when the confidence intervals overlapped and the additive values had the same sign. Individual QTL were named by letters indicating the related trait (Table 1), followed by the associated linkage group (LG) in Roman numerals (8) and an Arabic numeral when there were several QTL regions per linkage group. MapChart software (35) was used to produce visualizations of chromosomes carrying QTL.

The percentage of phenotypic variation explained by each QTL (R²) and their individual additive effects (a) were given by the model. The phenotypic variation explained by all detected QTL (R²t) was determined by multiple-regression analysis, using as explanatory variables the markers closest to the LOD score peak for each putative QTL.

For the earliness variable that did not fit well with the ANOVA prerequisite, a nonparametric test based on the Kruskal-Wallis statistic was also performed.

In addition to additive effects, digenic epistasis was tested with a two-way ANOVA model with interaction effects between all possible marker pairs.

To investigate marker x evaluation interaction effects, the following two-way ANOVA was performed: Y = μ + M + E + M × E + ε, where M is the effect of the marker, E is the effect of evaluation, and M × E is the marker x evaluation interaction effect.

Multiple regressions were performed with the R open-source package.

RESULTS

Trait performance. (i) Phenotypic evaluation of yield-related traits.

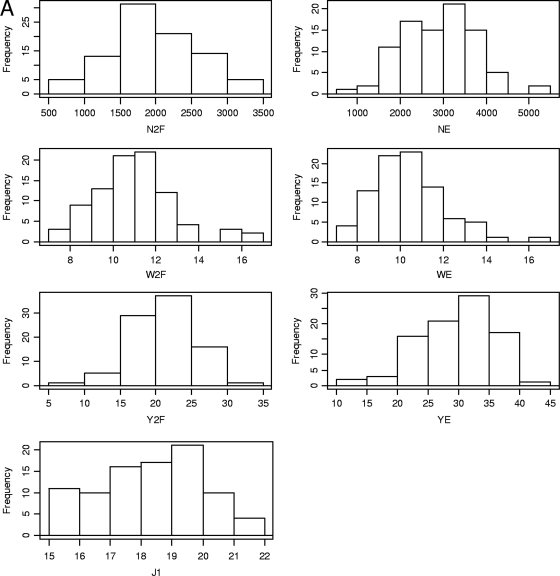
The phenotypic performance of the parental strains and the hybrids for each yield-related trait (Y, N, W, and J1) are presented per experiment in Table 1. The two parental strains exhibited contrasting phenotypes, with smaller but more numerous fruiting bodies per m² for the wild strain, JB3, than for the cultivar, U1. The difference between the two strains was significant (P < 0.05) for the number of fruiting bodies, with twice as many mushrooms for JB3. Conversely, the two parental strains were very close for the Y2F variable. U1 behaved worse than expected, but nevertheless, its yield values did not significantly differ from those obtained for the commercial lines used as controls in our experiment. The difference between the two parental strains was most pronounced for YE, suggesting an extended period of mushroom production for JB3. Considering the earliness trait, JB3 was ready to harvest before U1. Thus, compared to JB3, the first picking day for U1 was delayed for 3 or 5 days depending on the experiment. The JB3-83 × U1-7 first-generation hybrid displayed an intermediate value between those of the parental strains for most of the traits. The distribution of the H_i × U1-2 progeny showed continuous variation for all the yield-related traits (Fig. 1), suggesting that they were under quantitative and polygenic control. For most traits except earliness, transgressive segregation phenotypes were found, according to the SNK test (P < 0.05) (Table 1).

Fig 1.

Frequency distribution histograms for yield-related traits (A) and cap color parameters (B). Refer to Table 1 for x axis units.

ANOVA performed on the combined data across the two experiments revealed a major influence of the genotype (P < 10⁻⁶) and significant effects (P < 0.05) of experiment and/or G × E interactions for some traits (Table 2). These effects contributed to explaining between 4.3 and 17.7% of the phenotypic variance (results not shown). The highly significant (r_s > 0.4; P < 0.01) Spearman rank correlations, together with the concordance of the 20 highest-performing hybrids (>50%) (Table 1), suggested that G × E interactions were more likely due to changes in trait magnitude between the two experiments rather than to inconsistent behavior of genotypes. Given the significant G × E interactions, data from each trial were treated separately for the subsequent QTL analyses.

Table 2.

Analyses of variance, percentage of variance explained by the model (R²), coefficients of variation (CV), and heritability estimates (h²) for the yield-related traits and cap color parameters of the hybrid progeny in the two experiments H0513 and H0517 and the combined data

Expt	Source of variation	Yield-related traits														Color parameters
		N2F		NF		W2F		WF		Y2F		YE		J1		LF1		LF2		aF1		aF2		bF1		bF2
		df	MSa	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS	df	MS
Combined	G	88	1.3 × 106d	88	2.6 × 106d	88	13.65d	88	11.16d	88	75.1d	88	132.8d	88	10.33d	88	0.48d	87	0.4d	88	57.09d	87	44.4d	88	145.75d	87	123.16d
	E	1	1.2 × 106d	1	1.2 × 106	1	0.47	1	12.47c	1	149.6d	1	18.24	1	94.07d	1	0.04c	1	0.01	1	1.13	1	0.36c	1	12.9c	1	2.65
	G × E	88	2.5 × 105d	88	3.4 × 105c	88	3.07	88	1.65	88	13.5d	88	18.96b	88	1.57	88	5 × 10−3	84	0.01d	88	0.4	84	0.96d	88	1.4	84	1.83b
	B(E)	2	2.0 × 105	2	3.5 × 105	2	16.38c	2	13.75d	2	17.2	2	29.3	2	1.09	2	4 × 10−3	2	0.03c	2	1.69b	2	1.97c	2	4.3b	1	5.07b
	Error	176	1.2 × 105	176	2.2 × 105	176	2.76	176	2.76	176	5.76	176	13.22	176	1.6	175	4 × 10−3	161	4 × 10−3	176	0.36	176	0.39	176	1.31	171	1.31
	R2		0.87		0.87		0.75		0.8		0.88		0.85		0.8		0.98		0.98		0.99		0.98		0.98		0.98
	CV		16.8		16.2		14.5		11.5		10.7		11.9		6.6		10		9.85		13.7		16.5		8.6		6.8
	h2		0.81		0.87		0.77		0.85		0.82		0.86		0.84		0.99		0.98		0.99		0.98		0.99		0.99
H0513	G	88	8.5 × 105d	86	1.5 × 106d	88	9.87d	88	7.53d	88	48.04d	88	82.6d	88	5.43d	85	0.22d	87	0.2d	88	26.85d	87	22.21d	88	26.85d	87	62.3d
	B	1	2.6 × 105	1	5.8 × 104	1	31.81d	1	27.38d	1	22.87	1	31.44	1	1.62	1	4 × 10−3	1	0.03c	1	1.64c	1	3.51c	1	2.9	1	10.05c
	Error	88	1.1 × 105	86	1.5 × 105	88	2.73	88	1.84	88	5.87	88	13.74	88	1.16	85	3 × 10−3	87	3 × 10−3	88	0.22	87	0.37	88	0.99	87	1.15
	R2		0.89		0.88		0.79		0.81		0.89		0.86		0.82		0.98		0.98		0.99		0.98		0.98		0.98
	CV		15.5		15.5		14.3		12		10.5		12.1		5.4		9		9.7		10.6		15.9		5.8		6.34
	h2		0.87		0.87		0.72		0.76		0.88		0.83		0.79		0.99		0.98		0.99		0.98		0.99		0.98
H0517	G	88	7.6 × 105d	88	1.4 × 106d	87	6.17d	88	5.28d	88	40.58d	88	69.17d	88	6.47d	88	0.26d	84	0.21d	87	30.8d	84	23.98d	88	72.5d	84	64.5d
	B	1	1.5 × 105	1	1.5 × 104	1	3.49	1	0.12	1	11.6	1	27.2	1	0.56	1	5 × 10−3	1	0.02b	1	2.61b	1	0.44	1	5.7	1	0.1
	Error	88	1.3 × 105	88	2.4 × 105	87	2	88	1.39	88	5.66	88	12.7	88	2.05	88	5 × 10−3	84	5 × 10−3	87	0.39	84	0.41	88	1.63	84	1.48
	R2		0.85		0.86		0.71		0.79		0.88		0.85		0.76		0.98		0.98		0.98		0.98		0.98		0.97
	CV		18.1		16.9		14.6		10.8		11		11.8		7.6		10.9		10		16.35		17.1		7.3		7.3
	h2		0.83		0.83		0.6		0.74		0.86		0.82		0.68		0.98		0.98		0.98		0.98		0.98		0.98

^aMS, mean square.

^bP < 0.05.

^cP < 0.01.

^dP < 10⁻³.

Heritability was high for all the yield traits, ranging from 0.6 (W2F in H0517) to 0.88 (Y2F in H0513), indicating that most of the phenotypic variation appeared to be genetically determined. Highly significant correlations (P < 0.001) were detected between the two experiments, with Pearson coefficients ranging from 0.64 (W2F) to 0.77 (NE) (Table 3). For each experiment, significant correlations were observed between data for midproduction and the end of the trial.

Table 3.

Pearson's correlation coefficients between all traits in experiments H0513 (below diagonal) and H0517 (above diagonal)

Trait	Correlation coefficient
	W2F	WE	N2F	NE	Y2F	YE	J1	LF1	LF2	aF1	aF2	bF2	bv2
W2F		0.87a	−0.82a	−0.73a	−0.55a	−0.5a	0.06	0.02	−0.05	−0.01	−0.03	0.05	0.04
WE	0.93a		−0.78a	−0.84a	−0.56a	−0.61a	0.22	0.02	−0.07	0.01	0.04	0.07	0.08
N2F	−0.81a	−0.84a		0.85a	0.88a	0.72a	−0.17	0.05	0.13	−0.08	−0.09	−0.15	−0.13
NE	−0.72a	−0.83a	0.92a		0.75a	0.9a	−0.44a	0.03	0.13	−0.05	−0.09	−0.12	−0.14
Y2F	−0.48a	−0.55a	0.85a	0.81a		0.81a	−0.23	0.11	0.18	−0.16	−0.16	−0.21	−0.19
YE	−0.44a	−0.55a	0.75a	0.88a	0.89a		−0.51a	0.08	0.16	−0.12	−0.13	−0.16	−0.17
J1	0.19	0.28a	−0.4a	−0.47a	−0.42a	−0.51a		−0.08	−0.17	0.14	0.16	0.15	0.21
LF1	−0.21	−0.17	0.17	0.1	0.12	0.03	−0.08		0.96a	−0.99a	−0.96a	−0.96a	−0.95a
LF2	−0.2	−0.16	0.19	0.1	0.14	0.05	−0.07	0.97a		−0.94a	−0.99a	0.93a	−0.97a
aF1	0.21	0.18	−0.2	−0.14	−0.16	−0.08	0.12	−0.99a	−0.97a		0.95a	0.98a	0.96a
aF2	0.16	0.12	−0.16	−0.07	−0.14	−0.03	0.08	−0.97a	−0.99a	0.96a		0.93a	0.98a
bF2	0.27	0.24	−0.28a	−0.19	−0.24	−0.13	0.16	−0.96a	−0.95a	0.98a	0.94a		0.96a
bv2	0.21	0.21	−0.22	−0.18	−0.23	−0.13	0.2	−0.96a	−0.96a	0.97a	0.97a	0.98a

^aSignificant correlation (P < 0.01).

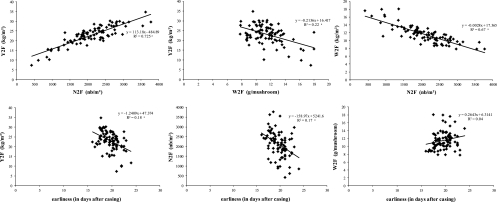
The yield was positively correlated with the number of mushrooms per m² but negatively correlated with the average weight (Table 3 and Fig. 2). The number of fruiting bodies per m² and the average weight of a fruiting body were negatively correlated, underlining the fact that the higher the number of fruiting bodies, the lower the average weight. These results were not surprising, due to the triangular relationship between these variables. However, the absolute correlation value between yield and number of fruiting bodies was greater (more than 0.75) than that between yield and fruiting body average weight (up to 0.55), indicating that the number of mushrooms outweighed the yield.

Fig 2.

Scatter plots showing relationships between several pairs of variables: Y2F against N2F and W2F; W2F against N2F; and earliness against Y2F, N2F, and W2F in the experiment H0513. Regression lines are drawn according to the corresponding linear regression equation. The coefficient of determination (R²) is indicated. ^a, significant correlation (P < 10^–3).

A negative correlation was also observed between earliness and yield (Table 3). The earliest genotypes tended to produce numerous but small mushrooms (Fig. 2). In general, the correlation of earliness was higher with the final variables than with the midproduction variables. In addition, earliness was found to be negatively correlated with the efficient cropping period (data not shown). The earliest hybrids showed a production spread throughout the whole cropping period, whereas the latest productive hybrids tended to produce mainly during the first two flushes under our experimental conditions. Some hybrids did not show a fourth flush (11.23% and 7.86% in H0513 and H0517, respectively). For some of them (5 in H0513 and 6 in H0517), this may be due to the fact that all the crops were stopped at the same time, and these hybrids were supposed to be able to do a 4th flush with a longer cropping period.

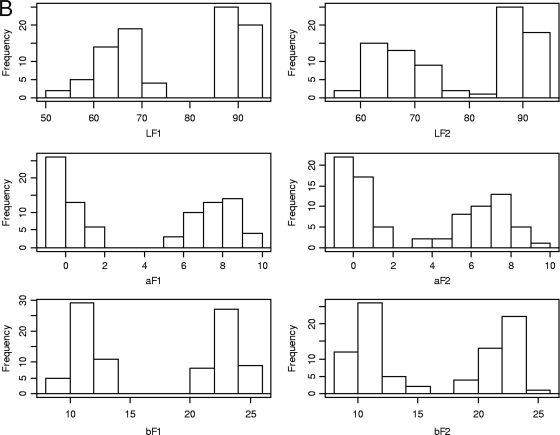
(ii) Cap color parameters.

A bimodal distribution was observed for each color parameter (Fig. 1). Very high correlations were found (r_p > 0.96; P < 10⁻⁵) between the first and second flushes and between the two experiments. Analyses of variance revealed the variability among the hybrids for the cap color parameters (P < 10⁻⁶) (Table 2). Considering arbitrarily two balanced color classes of hybrids based on L values (limit, 80, fixed from the bimodal distribution), genetic variability within each class was also highly significant, and it was found to be greater in the brown subgroup than in the white one. Very high heritability (h² > 0.98) was estimated for the cap color parameters. No significant correlation was found between the yield-related traits and the cap color variables. In addition, no significant difference for yield traits was observed between the brown and the white hybrids (t test; P < 0.01).

QTL detection.

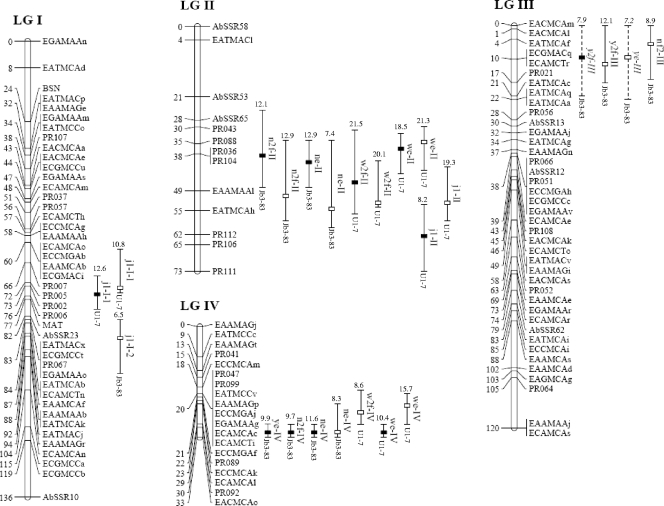
Only results obtained from the CIM procedure are presented for each trait and each experiment (Table 4 and Fig. 3). Empirical thresholds determined after 1,000-permutation LR tests were very similar, ranging from 2.32 to 2.74, depending on the trait and the experiment. Thus, an average LOD threshold of 2.5 was used to declare a QTL significant. Also, in order to compare the two experiments, genomic areas highlighted for one of the experiments were also checked for QTL with a LOD score between 2.0 and 2.5.

Table 4.

QTL for yield-related traits and cap color parameter (logitL) detected in the second-generation hybrid progeny derived from the crossⁱ

Trait	H0513										H0517
	QTL	LG	Markera	Position (cM)b	LODc	CI position (cM)d	Parental allelee	Additive effect	R2 (%)	R2t (%)	QTL	LG	Marker	Position (cM)	LOD	CI position (cM)	Parental allele	Additive effect	R2 (%)	R2t (%)
Y2F	y2f-III	III	ECAMCTr	9.6	2.25	0–21	Jb3-83	2.82	7.9	25.2	y2f-III	III	ECAMCTr	11.6	2.65	0–17	Jb3-83	3.24	12.1	20.8
	y2f-X	X	ECGMACv	57.4	3.35	45–65	Jb3-83	3.54	12.1		y2f-X	X	ECGMACv	57.4	2.01	45–64	Jb3-83	5.04	8.7
YE											ye-III	III	ECAMCTr	9.6	2.22	0–22	Jb3-83	3.31	7.2	33.3
	ye-IV	IV	PR092	31.3	2.75	29–end	Jb3-83	6.70	9.9	22.8
	ye-X	X	EAAMAGh	55.4	3.63	45–65	Jb3-83	4.73	12.9		ye-X	X	PR082	47.1	6.40	41–55	Jb3-83	5.81	23.2
N2F	n2f-II	II	PR088	38.1	3.05	25–48	Jb3-83	506.62	12.1	30.9	n2f-II	II	PR036	50.1	3.17	34–58	Jb3-83	448.60	12.9	23.1
											n2f-III	III	EATMCAf	5.5	2.61	0–16	Jb3-83	378.63	8.9
	n2f-IV	IV	PR092	31.3	2.68	29–end	Jb3-83	688.30	9.7
	n2f-X	X	PR082	49.1	3.34	41–57	Jb3-83	456.87	11.4
NE	ne-II	II	PR088	40.1	2.77	34–48	Jb3-83	935.53	12.9	35.9	ne-II	II	EAAMAA1	54.1	2.50	34–59	Jb3-83	458.36	7.4	33.2
	ne-IV	IV	PR092	31.3	3.67	29–end	Jb3-83	1001.11	11.6		ne-IV	IV	PR092	31.3	2.60	23–end	Jb3-83	505.35	8.3
	ne-X	X	PR082	47.1	4.69	41–51	Jb3-83	682.72	14.5		ne-X	X	EAAMAGh	51.4	4.15	47–61	Jb3-83	637.60	13.1
W2F	w2f-II	II	PR088	46.1	5.10	31–56	U1-7	2.10	21.5	21.5	w2f-II	II	PR36	52.1	4.88	40–54	U1-7	2.60	20.1	23.2
											w2f-IV	IV	ECCMCAk	25.3	2.51	19–29	U1-7	1.13	8.6
WE	we-II	II	PR088	36.1	5.23	32–44	U1-7	1.83	18.5	39.5	we-II	II	PR088	34.1	6.40	30–43	U1-7	1.61	21.3	35.5
	we-IV	IV	PR092	31.3	3.34	22–end	U1-7	1.33	10.4		we-IV	IV	ECCMACk	23.3	4.97	20–29	U1-7	1.33	15.7
	we-XI	XI	PR090	48.1	2.50	42–56	Jb3-83	1.10	7.6
J1	j1-I	I	PR006	75.3	5.2g	70–80	U1-7	1.52	12.6	56.3	j1-I-1	I	PR002	73.3	4.56f	62–74	U1-7	2.30	10.8	58.8
											j1-I-2	I	EATMACj	88.6	2.60	83–99	Jb3-83	1.62	6.5
	j1-II	II	EATMCAh	62.3	3.94g	53–74	U1-7	1.22	8.2		J1-II	II	EAAMAA1	52.3	7.54h	42–58	U1-7	2.01	19.3
	j1-V	V	EATMACn	25.8	4.5h	9–30	U1-7	1.42	10.9		j1-V	V	EATMACn	31.9	2.7g	24–end	U1-7	1.04	5.7
	j1-X	X	EATMCAm	45.2	8.25h	43–48	U1-7	2.02	22.4		j1-X	X	EATMCAm	47.1	8.52h	45–61	U1-7	2.15	19.8
											j1-XI	XI	EGCMCGa	33.4	3.84f	28–38	Jb3-83	1.23	8.1
logLF1	lf1-VIII	VIII	Ppc1	65.16	51.2	61–68	U1-7	0.62	86.3	89.8	lf1-VIII	VIII	Ppc1	65.16	57.8	62–68	U1-7	0.70	89.2	89.8
	lf1-XIII	XIII	EATMCCt	33.9	2.34	32–end	U1-7	0.08	1.5		lf1-XIII	XIII	EATMCCt	33.9	2.8	32–end	U1-7	0.10	1.8
logLF2	lf2-VII	VII	EATMCCk	12.6	2.75	2–14	U1-7	0.10	2.2	88.0	lf2-VII	VII	EATMCCk	10	2.97	2–14	U1-7	1.1	2.92	87.1
	lf2-VIII	VIII	Ppc1	65.16	42.5	62–68	U1-7	0.58	85.7		lf2-VIII	VIII	Ppc1	65	38.9	62–68	U1-7	0.61	84.5
	lf2-XIII	XIII	EATMCCt	33.9	3.8	26–end	U1-7	0.1	3.1		lf2-XIII	XIII	EATMCCt	33.9	2.96	32–end	U1-7	0.11	2.67

^aNearest upstream marker to the LOD score peak.

^bPosition of the LOD score peak in cM.

^cLOD score value at the LOD score peak.

^dLOD-1 support intervals.

^eParental alleles that contribute to increase the trait values.

^fKruskal-Wallis test; P < 0.05.

^gKruskal-Wallis test; P < 0.01.

^hKruskal-Wallis test; P < 10⁻³.

ⁱQTL detected with 2 < LOD score < 2.5 are in italics.

Fig 3.

Map positions of the significant QTL on the A. bisporus linkage map. Only linkage groups for which QTL were found are shown. Positions are given in cM (Kosambi units) to the right of the linkage groups. The QTL nomenclature is described in the text. The position of the maximum LOD value is indicated by a box, black for experiment H0513 and white for H0517. LOD-1 confidence intervals are represented by plain lines for QTL with LOD scores of >2.5 and by dashed lines for QTL with 2 < LOD score < 2.5. The R² value of each QTL and the parental allele that contributed to increase the trait are given at the top and bottom of the confidence intervals, respectively.

Epistatic interactions were tested for each trait between the 217 markers of the framework map. With 23,436 tests performed per trait, a significance threshold at a P value of <10⁻⁵ was chosen. Thus, less than one (0.23) interaction could occur by chance. At this threshold, no significant epistatic interaction was identified between markers.

No significant marker x evaluation interactions were indicated by multiway ANOVA (P < 10⁻³).

Yield-related traits.

Across the seven yield-related traits, 18 and 19 QTL were detected for experiments H0513 and H0517, respectively (Table 4). Consistencies between experiments were found for most of the QTL. Some QTL were specific to one experiment, such as ye-III or we-XI, which were found only in H0517 and H0513, respectively.

Depending on the trait, up to six QTL were detected, with individual R² values ranging from 5.7% (j1-V in H0517) to 23.2% (ye-X in H0517). The total phenotypic variation explained by all the QTL (R²t) ranged from 20.8% for the yield trait in H0513 to 58.8% for the earliness trait in H0517. The traits with the highest R²t value were earliness (4 to 6 QTL; R²t > 56), followed by the number of fruiting bodies per m² (2 or 3 QTL; R²t > 23.1), the average weight per mushroom (up to 3 QTL; R²t > 21.5), and the yield (2 or 3 QTL; R²t > 20.8).

For the number of fruiting bodies and the yield, the alleles that increased the trait values came from the wild parent, JB3-83. Conversely, for the weight of fruiting bodies, the allele derived from the parental cultivar strain U1 contributed to increase the trait values. Considering earliness, for j1-I-1, j1-II, j1-V, and j1-XI, the U1 contributing alleles were associated with higher values, i.e., with tardiness. For the two QTL j1-I-2 and j1-XI, observed only in H0517, the JB3-83 allele delayed the first harvest day.

The overlapping of QTL confidence intervals revealed clusters of QTL governing several distinct traits. Indeed, four genomic regions located on linkage groups II, III, IV, and X were involved in weight, number, and yield scores. Two genomic regions, on LGII and LGX, appeared to also be shared by these traits and earliness. However, large confidence intervals were drawn on LGII, whatever the trait considered.

Cap color parameters.

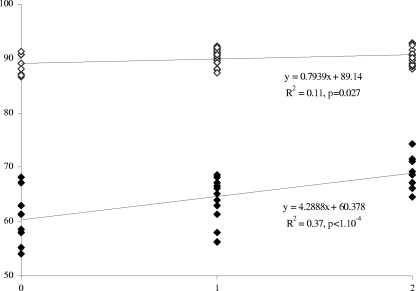
As the QTL analysis of the a and b parameters did not provide useful additional information (data not shown), only the results of QTL detection for the logitL variable are presented. In addition to the major QTL (R² > 84%) controlling cap color located on LGVIII in the vicinity of the PPC1 locus, two other genomic regions were detected by CIM, on LGVII and LGXIII. The phenotypic variation of the lightness explained by all the QTL reached 89.8%. Thus, the favorable alleles present at these two additional QTL contributed to lighten the cap color of the hybrids, as illustrated by the higher value of the lightness (Fig. 4). This was particularly significant for the brown hybrids, and it explained the variability observed within them.

Fig 4.

Effects of favorable alleles at the two additional QTL, other than the PPC1 locus, found for cap color parameters on the lightness value in the hybrid progeny. Zero corresponds to no favorable allele at the two additional QTL. The variation in cap color is explained only by the segregation at the PPC1 locus; 1 and 2 stand for one favorable allele for either of the two additional QTL and two favorable alleles at the two additional QTL, respectively.

DISCUSSION

The QTL involved in the inheritance of crop production traits provide a picture of their genetic complexity, and the location of the major loci should be informative for genetic analysis and breeding in A. bisporus. To our knowledge, this is the first QTL detection of yield-related traits for this species.

General features and accuracy of QTL detection.

The use of a comprehensive genetic map combined with a composite interval-mapping procedure strengthens our QTL results. Indeed, the framework map used in this study was built using markers spaced on average every 6 cM and evenly spread over the genome (8). This average distance between markers contributed to better precision of the QTL position by reducing the confidence interval and limiting discrepancies in the explained phenotypic variance due to incomplete linkage between the QTL and the marker inferred in the multiple-regression model (5). However, we observed some inconsistencies in QTL detection on LGII. Quantitative trait loci with high LOD values (from 2.5 to 7.5) but large confidence intervals were undoubtedly revealed. This could be attributed to biases in marker segregation previously observed on this linkage group (8), which might have decreased the power of QTL detection, as proposed by several authors (37, 39). Analysis by CIM increased control of the genetic background and the resolution of QTL mapping. It also provided a more accurate estimation of R² values and additive effects (21, 40). In our study, CIM made it possible to detect additional QTL compared to simple interval mapping (data not shown). The use of replicate experiments also increased the statistical power of QTL detection (12), and the observed consistency of the results between the two trials validates the QTL detection (13).

The highly significant correlations between the two experiments validate the reproducibility of the phenotypic evaluations for the yield-related traits. The stable behavior of the hybrids conferred high heritability estimates (0.68 to 0.90), indicating that the variations observed within the progeny are mostly genetically controlled. However, the detected QTL together explained from 20.8 to 58.8% of the phenotypic variation for the different yield-related traits, while the heritability values were quite comparable, suggesting that all the genetic variation is not explained by these QTL. Several hypotheses may support these results. First, the small size of the population used in this study (89 hybrids) can lead to an underestimation of QTL numbers, an overestimation of QTL effects, and biases in the estimated proportions of the total genotypic variance (21, 32, 33). Thus, some QTL with low individual effects may remain undetected. Second, in A. bisporus, the linkage mapping is performed using haploid progeny (homokaryons), whereas the evaluation of numerous important agronomic traits is only possible at the dikaryotic stage, after crossing with a compatible tester. This peculiarity, common to numerous edible mushrooms, may lead to inconsistencies in QTL detection (16). Indeed, our QTL-mapping procedure relies on the allelic-substitution effects of the segregating nuclei, together with their interaction with the constant tester nucleus (16). Therefore, the differential effect might not be sufficient to reveal significant marker-trait association.

Genetic architecture of yield-related traits.

Analyses of correlations between yield components showed that the average weight of fruiting bodies decreased when the yield and the number of mushrooms increased, as demonstrated in previous studies (27). Given these negative relationships, the development of high-yield genotypes able to produce mushrooms with a high average weight may be challenging.

Among the progeny, several hybrids exhibited high yields (30 to 35 kg/m²) and quite good average weight (>10 g/mushroom). Whereas these values were quite a bit lower than the usual commercial criteria, particularly the average weight, the further development of new hybrids is conceivable. We also observed that the earliest hybrids tended to produce a higher number of smaller mushrooms, as already underlined by Xu (38), with production spread throughout the whole cropping period. Similar relationships between these productive traits have been described in another edible mushroom, P. ostreatus (15). This variability in earliness could be useful in developing new hybrid strains that cover the range of commercial mushroom outlets. Indeed, for the fresh market, genotypes with a harvest spread across several days facilitate hand picking, whereas for the canning industry, varieties for which all the mushrooms come simultaneously into the expected maturity stage are preferred for mechanical harvesting. Moreover, genotypes bred for earliness would be expected to be more tolerant of dry bubble (7).

All the yield-related traits are under polygenic control, mainly by small-effect QTL, as the individual R² values never surpassed 23%. No significant epistatic interaction was detected in our study, whatever the trait under consideration, suggesting that loci involved in trait variation acted additively. Accordingly, the total R² values were similar to the arithmetic sum of the individual QTL R² values.

Four genomic regions on LGII, -III, -IV, and -X were found to be involved in the genetic control of yield, average weight, and number of mushrooms per m². It was not surprising to find colocation between these traits due to their mathematical relationship. Such clusters of QTL were also observed in P. ostreatus for comparable productivity traits (15). However, the decomposition of the yield into the two elementary components, number and weight, made possible a refined analysis of the genetic parameters controlling this trait. More QTL were detected with a higher LOD score for the N and W variables together rather than for the Y variable alone. The colocations of QTL observed are also in agreement with the correlations found between traits. It is difficult to determine whether these QTL colocations are due to the pleiotropic effect of a single locus or to effects of closely linked genes. Only fine mapping would provide additional information on the linkage versus pleiotropic genetic determinism of these traits. Some QTL were found to be specific to one experiment, reflecting G × E interactions. Despite the controlled environment of the cultivation room, microvariations in temperature and moisture could not be completely excluded and may have impacted the behavior of the hybrids. The compost batch was not the same in the two experiments, and thus, the compost quality might have varied and affected the crop production.

Considering the cap color trait, our results are in agreement with a previous study that described the cap color as being governed by the major locus PPC1 (3). Thanks to the saturated linkage map used in this study, together with lightness and chromaticity measurements, the QTL analysis with composite interval mapping made it possible to refine the inheritance of the cap color trait, since two additional loci were found. The phenotypic variation explained by all the QTL, associated with the high heritability values, suggests that undetected QTL are unlikely. We have also demonstrated that lightness and chromaticity are under the same genetic control. While the PPC1 locus was found to be recessive for the white color (3), our data did not allow us to establish the dominance status of the two new loci, since only additive effects could be estimated. Such oligogenic control of cap color has already been suggested (24, 27), and this assumption is coherent with the variability observed for this trait in genetic resources (2, 24).

For breeding purposes, the wild germ plasm of A. bisporus is a valuable source of variability for several important agronomic traits, such as yield and resistance to disease (2, 14, 27). Accordingly, it is not surprising to find that the wild parental strain JB3 brought favorable alleles for some of the studied traits (earliness, yield, and number of mushrooms per m²). Nevertheless, the use of wild strains in mushroom breeding could be hampered by the introduction of undesirable traits, as illustrated in our study by the decrease in average mushroom weight. Other detrimental traits for mushroom production, such as bruising, cap scaling, or stipe brittleness, were also observed among the progeny (data not shown). A repeated backcrossing strategy can be applied in mushroom breeding to introgress the trait of interest derived from a wild line into a recipient commercial strain while limiting unfavorable linkage drag (30).

In conclusion, our results provide a solid foundation for further investigation into the biological mechanisms controlling productive traits in the white button mushroom. The recent release of the reference genome sequence of A. bisporus (http://genome.jgi-psf.org/Agabi_varbisH97_2) will help to further the understanding of genomic loci underlying quantitative traits through the identification of potential candidate genes, targeted marker design for fine mapping, or genetic/genomic experiments (25, 36). Furthermore, the QTL-marker associations highlighted in the present study, together with the QTL analyses of dry-bubble resistance described in the companion paper (8a), are valuable tools to make up multitrait marker-based breeding strategy in this fungus.