Achievable Convergence Angle and the Effect of Preparation Design on the Clinical Outcome of Full Veneer Crowns in Dogs

Summary

It is widely accepted that the convergence angle of a full veneer crown preparation should be as close to parallel as possible to attain adequate retention/resistance. The shape of the dog’s canine tooth limits the veterinary dentists’ ability to achieve the recommended convergence angle. However, the clinically achievable convergence angle of the canine tooth in dogs has not been evaluated. In addition, the convergence angle and other physical properties of a preparation, such as height and base diameter, have been shown to affect the retention/resistance of full veneer crowns, in vitro. This effect has not been evaluated clinically in the dog. Physical properties of 32 stone dies from full veneer crowns of canine teeth were studied to evaluate the clinically achievable convergence angle and the potential effect physical properties of the preparation had on the clinical outcome of the restoration. The clinically achievable convergence angle was much higher than the current recommendation. There was an association, albeit not statistically significant, between physical properties of a preparation (convergence angle, height, base diameter) and the clinical outcome of the restoration.

Introduction

To achieve clinical success of full metal crown therapy in the dog, the veterinary dentist must use an appropriate preparation design. The preparation design is guided by five principles: preservation of tooth structure, retention and resistance, structural durability, marginal integrity, and preservation of the periodontium.¹ For a restoration to have longevity in the oral cavity, a preparation should have retention and resistance form. The concept of retention form refers to the ability of a restoration to resist forces along the long axis, or path of insertion, of the tooth.¹ Resistance form works in tandem with the concept of retention. Resistance form prevents dislodgement of the restoration under occlusal forces directed in an apical or oblique direction.¹ A preparation either has retention/resistance form or it does not.²

Convergence angle is one of four operator-controlled factors in tooth preparation that influence retention/resistance. Some confusion has been perpetuated in the literature regarding the terms taper and convergence angle. These terms are often inappropriately used synonymously to describe a gradual decrease in the width of an elongated object. For the purposes of this manuscript, we will use the following nomenclature: Taper is the angle between one axial wall of the preparation and the long axis of the preparation. Convergence angle is defined as the angle between two opposing axial walls of a preparation and equals the sum of the taper of two opposing axial walls (Fig 1).

Figure 1.

Photograph of a stone die depicting the difference between taper (T) and convergence (CA) angles.

A strong relationship has been shown to exist between the retention/resistance form of a preparation and the convergence angle. The ideal convergence angle has been reported to be between 3 and 14°.¹ Convergence angles higher than this are said to have inadequate resistance/retention form. Further, an interdependent relationship has been established between convergence angle, preparation height, and preparation base diameter in which the acceptable convergence angle for resistance depends on preparation height and base diameter.³ As the preparation height increases, for a given base diameter, the maximal allowable convergence angle that will maintain adequate resistance form also increases.³ This relationship can be considered as a height (H) to base diameter (D) ratio (H/D).²

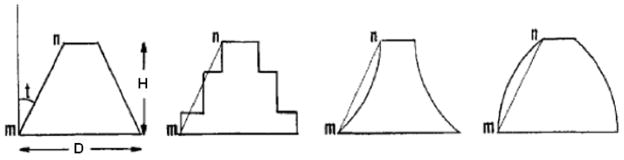
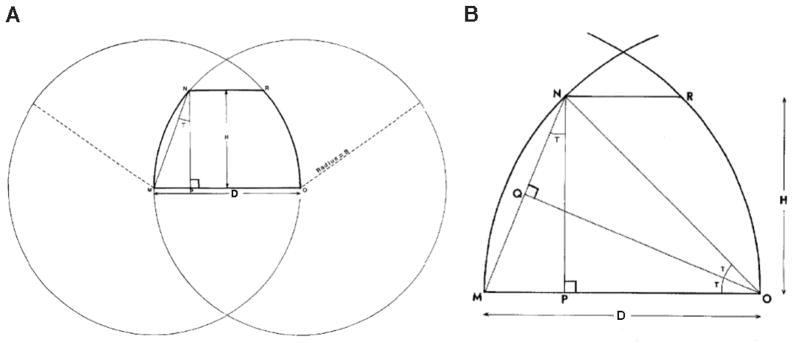
The H/D has been used to establish conceptual guidelines for taper in humans.² Briefly, this concept is based on the theoretical foundation that resistance form is either present or absent. If one were to try to roll a crown off a die, resistance form is either present (and the operator cannot roll the crown off) or absent (and the operator easily rolls the crown off). The point at which resistance form is lost is recognized as a minimally acceptable taper and is designated the limiting average taper. Tapers lower than this value do have resistance form and those greater do not have resistance form. The limiting average taper can be calculated with the formula T = ½ arcsin (H/D). This formula was first arrived at by first considering that, regardless of shape, every preparation has an average taper (Fig. 2).² The authors then considered a representative preparation in which the taper at every point was equivalent to the limiting taper (Fig. 3). The opposing sides of the preparation represent the arc of two intersecting circles. The center of each circle represents the opposing preparation margin. Thus, the radius of each circle is equal to the base diameter. Intuitively, one can see that the preparation does not have resistance form because the preparation sides are the arc of a circle. In other words, if one were to try to roll a crown off the preparation, it would easily roll off along the arc of the circle. If the taper were to be smaller, it would then have resistance form. The authors then added lines OQ and ON to solve for the limiting average taper (T). Using similar triangles MNP, MOQ, and NOQ, it is seen that angle PON is equal to 2T. Therefore, the sine of angle PON equals the sine of 2T that also equals PN/NO. Line NO is the radius of the circle, which, as discussed earlier, is the preparation base diameter (D). Line PN is the preparation height (H). Thus, sin 2T = PN/NO or sin 2T = H/D. The inverse function then yields 2T = arcsin (H/D) or T = ½ arcsin (H/D). Therefore, the limiting average taper is ½ arcsin (H/D). Each preparation will have a distinct H/D that can be used to determine what taper is clinically acceptable.

Figure 2.

Figure depicting the concept of average taper. All four of these preparations have the same average taper even though the shape of each one is different. The average taper of each preparation equals the taper of line mn, which is shown by angle t in the first preparation.

(Modified with permission from Parker MH, Calverley MJ, Gardner FJ, et al. New guidelines for preparation taper. J Prosthodont 1993; 2:61–66.2)

Figure 3.

Figure (A) depicting the mathematical basis for the concept of the limiting average taper.² Each side of the preparation is formed by the arc of a circle with its radius equal to the base and its center of rotation the opposing margin. Because the taper at each point on the side is as small as possible without providing resistance form, the taper of line MN (defined as the limiting average taper) must also be as small as possible without providing resistance form. When (A) is modified in order to solve for the taper of line MN (B), the sine of 2T equals NP/NO or H/D, T is equal to arcsin (H/D).

(Modified with permission from Parker MH, Calverley MJ, Gardner FJ, et al. New guidelines for preparation taper. J Prosthodont 1993; 2:61–66.2)

Multiple studies in humans have indicated that the recommended convergence angle is rarely obtained. Despite this revelation, and the obvious anatomical differences of the canine tooth in dogs, the current veterinary recommendation echoes the recommendation for humans.^4,5 The unique anatomical features of the canine tooth in dogs make achieving this recommendation unlikely, if not impossible. However, the feasibility of achieving the recommended convergence angle has not been evaluated in dogs. In addition, studies in humans have shown that convergence angles of clinically successful preparations exceed the recommended values.⁶ Anecdotally, veterinary dentists would likely affirm this sentiment. However, no evidence-based clinical recommendations have been offered for prosthodontic treatment of teeth in dogs. The aims of this study are to establish the clinically achievable convergence angle and evaluate what effects the preparation convergence angle, height, and base diameter may have on the clinical outcome of full crown restoration of the canine tooth in dogs. Also, to evaluate the utility of the concept of limiting average taper in the dog and offer clinical guidelines for crown preparation. Specifically, our hypotheses are: 1) the clinically achievable convergence angle for the canine tooth in dogs exceeds the current recommendations; 2) because of the natural anatomical variation in the inclination of the distal axial wall of the canine tooth in dogs, the clinician’s ability to achieve a low convergence angle will depend on the height of the tooth. Stated another way, as H/D increases, the achievable convergence angle will decrease; 3) those preparations with a high H/D will be more successful than those with a low H/D; 4) those restorations that “fall off ” will have a higher convergence angle than the restorations that do not “fall off ”; 5) the concept of limiting average taper can be used to guide the veterinary dentist in preparation design.

Materials and Methods

Physical properties of preparations were measured/calculated on 32 stone dies of maxillary and mandibular canine teeth from the collection of the Dentistry and Oral Surgery Service of the University of Wisconsin-School of Veterinary Medicine’s Veterinary Medical Teaching Hospital. The dies originated from single unit full veneer preparations of clinical patients, performed by either residents in dentistry and oral surgery or a board-certified veterinary dentist between 2002 and 2008. At the time of treatment, the clinicians were not aware of any future study regarding the preparation. The dies were randomly assigned a numerical identification and marked with an indelible felt tip marker^a on the facial aspect. Dies were then entered into a spreadsheet^b by patient name and numerical identification. The achievable convergence angle (CA), preparation base diameter (D), and preparation height (H) were measured. The H/D and the limiting average convergence angle (CA_lim) were then calculated based on these measurements. A description of the specific methodology of the measurements/calculations is provided below.

Achievable Convergence Angle

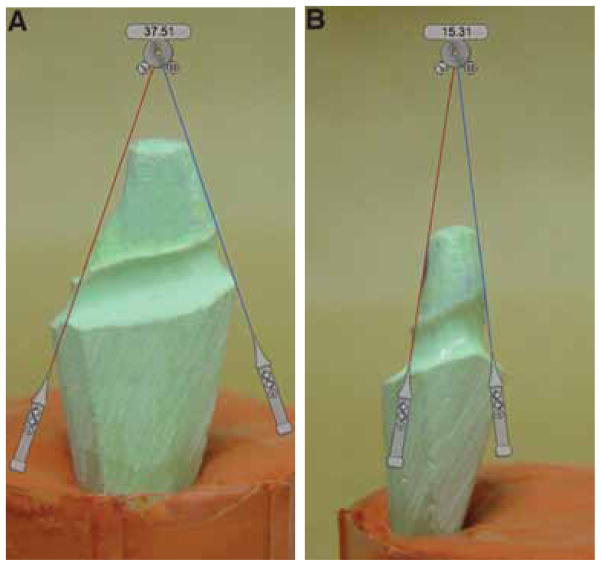
Each die was photographed with a digital camera^c in two planes (faciolingual and mesiodistal). The faciolingual (FL) image allowed measurement of the CA between the facial and lingual axial walls (CA-FL). The mesiodistal (MD) image allowed measurement of the CA between the mesial and distal axial walls (CA-MD). The digital images were uploaded into a designated folder within the hospital server on a desktop computer^d. Individual image files were named by the numerical identification followed by MD or FL for directional description. Digital images were captured in a continuous manner and obtained with macro setting for optimal detail. Software^e with a digital protractor tool was used to measure the CA for the MD and the FL images. CA measurements were determined by superimposing the digital protractor over the individual die’s digital image. Due to the natural anatomical variation in the inclination of the axial walls of the canine tooth, the average CA was used based on a previous study (Fig 2).² One side of the digital protractor was aligned along the best-fit line connecting the preparation margin to the preparation cusp. The other side of the digital protractor was aligned similarly on the opposite axial wall to provide for the average CA (Fig. 4). The CA-MD and CA-FL for each preparation was measured by three blinded, independent examiners (JWS, CJS, JR) for a total of three measurements per die. The mean CA-MD and CA-FL for each preparation were then calculated. Finally, the CA-MD and CA-FL means were combined to determine an overall mean preparation CA (CA-O).

Figure 4.

Photographs of stone dies depicting the digital method used in this study to measure the mesial-distal (A) and facial-lingual (B) convergence angles [CA], CA-MD and CA-FL, respectively.

Preparation Height and Diameter

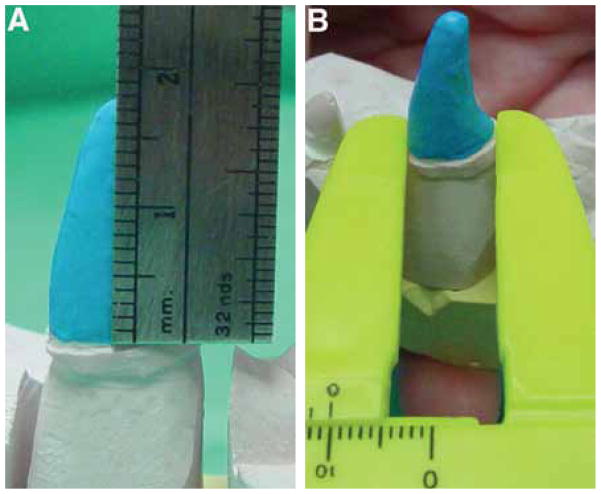
Preparation height was measured directly from each preparation with a stainless steel ruler^f. Measurements were made from the gingival preparation margin to the most coronal point of the preparation along the facial axial wall. Preparation base sdiameter was measured from the mesial axial wall to the distal axial wall (D-MD) at the level of the preparation margin using vernier calipers^g and recorded for each die (Fig. 5). Preparation base diameter was also measured and recorded from the facial axial wall to the lingual axial wall (D-FL) at the level of the preparation margin using the same vernier calipers. The D-MD and D-FL were averaged to calculate an overall mean preparation base diameter (D-O). All measurements were performed in a continuous fashion by a single investigator (JR) for consistency.

Figure 5.

Photographs of stone dies depicting the method used in this study to measure preparation height (A) and base diameter (B).

Preparation Height/Diameter Ratio

Using formula calculating capabilities of the spreadsheet software^b, the height to mesiodistal base diameter ratio (H/D-MD) and the height to faciolingual base diameter ratio (H/D-FL) were calculated and recorded for all preparations. The H/D-MD and H/D-FL were combined to determine an overall mean preparation H/D (H/D-O).

Limiting Average Convergence Angle

The limiting average CA was utilized instead of limiting average taper to allow direct comparison with the CA measured in the study. The limiting average convergence angle was calculated for the mesiodistal angle (CA_lim-MD), the faciolingual angle (CA_lim-FL), and the overall preparation (CA_lim-O) according to the following formulas: CA_lim = 2T_lim and T_lim = ½ arcsin (H/D) where T_lim is the limiting average taper of a single axial wall; and CA_lim is the sum of the T_lim of two opposing axial walls; and H is the preparation height; and D is the preparation base diameter; thus CA_lim = 2[1/2 arcsin (H/D)] or CA_lim = arcsin (H/D).

For teeth with an H/D greater than 1.0, the height is greater than or equal to the base diameter and no CA_lim exists. Thus, for all dies with a H/D greater than or equal to 1.0, any CA would theoretically provide adequate resistance form.

Clinical Outcome

The medical records of all patients corresponding to the preparations were reviewed to determine the clinical outcome of the restoration and recorded as one of three outcomes: Adhesive/Cohesive failure- this is a failure of either the bond between the cement and the tooth or between the cement and the restoration or within the internal bond of the cement. For the purposes of this study, this type of failure was considered a failure in retention/resistance form. Tooth fracture failure- this is not a bond failure and is represented by a tooth crown fracture with some of the natural crown still adhered to the interior surface of the restoration. Although a tooth fracture is considered a clinical failure, for the purposes of this study, a tooth fracture was not considered a failure in retention/resistance form. Non-failure- crown still intact at time of data collection.

For those patients that did not have a recent clinical examination and for those that did have a recent clinical examination but no specific mention of the restoration was noted in the medical record, owners were contacted by telephone and information regarding restoration presence or absence was obtained.

Statistical Analysis

All preparation measurements and calculations (CA, H, D, H/D, CA_lim) were expressed as the mean ± SD. Data ranges were also recorded. Where appropriate, MD and FL means ± SD were averaged to calculate an overall preparation mean ± SD. Inter-examiner reliability for measurement of CA was estimated using the intraclass correlation coefficient (r). The relationship between H/D and CA was evaluated by calculating the Spearman correlation coefficient (ρ). One-way analysis of variance (ANOVA) was utilized to evaluate any associations between preparation measurements/calculations and the clinical outcome. A value of P ≤ 0.05 was considered indicative of statistical significance.

Results

Achievable Convergence Angle

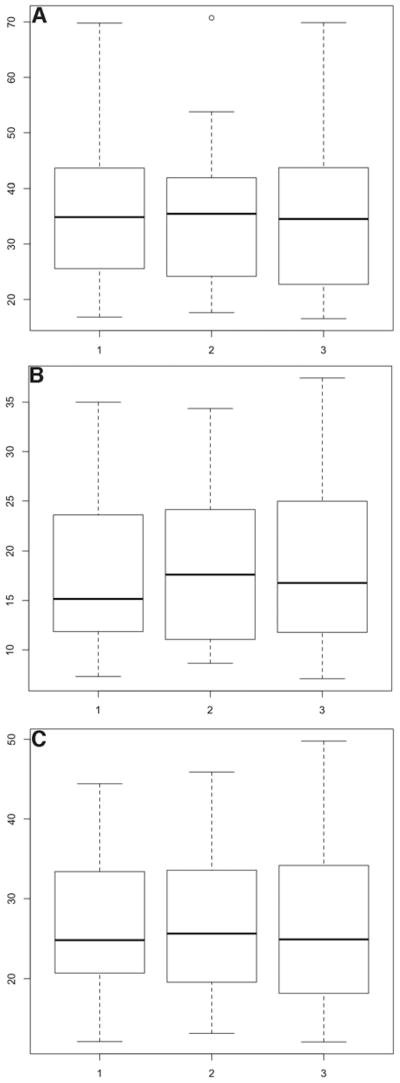
The mean ± SD for CA-MD was 35.50 ± 1.99 (range = 17.01° – 70.14°). The mean ± SD for CA-FL was 18.48 ± 1.51 (range = 7.86° – 35.6°). The mean ± SD for CA-O was 26.71 ± 1.75 (range = 12.43° – 46.70°). The degree of inter-examiner reliability for CA measurements was found to be high (r = 0.9813 for CA-MD, r = 0.9792 for CA-FL) (Fig. 6).

Figure 6.

Boxplots depicting the inter-examiner variability for mesial-distal (A), facial-lingual (B), and overall (C) convergence angles [CA], CA-MD, CA-FL, and CA-O, respectively. Examiners are plotted on the x axis and CA (in degrees) is plotted on the y axis.

Table 1 shows the percentage of preparations distributed among three categories (< 12°, 12.1° – 25°, and > 25°). The first cut-off point (< 12°) was chosen because it has traditionally been considered the upper limit of the recommended convergence angle range. The other categories were chosen arbitrarily. When considering CA-MD, 0/32 (0 %) were within the recommended range. When considering CA-FL, 10/32 (31.25 %) were within the recommended range. When considering the overall preparation (CA-O), 0/32 (0 %) were within the recommended range.

Table 1.

Distribution of preparations according to convergence angle (CA) ranges.

	Achievable CA
	*< 12.0	12.1 – 25	> 25
CA-MD	0 %	25 %	75 %
CA-FL	31.25 %	46.88 %	21.87 %
CA-O	0 %	50 %	50 %

MD = mesiodistal; FL = faciolingual; O = overall

Red = recommended* and arbitrary range caregories; blue = actual measurement distribution

Preparation Height and Diameter

The mean ± SD for preparation height was 11.24-mm ± 3.48 (range = 6.5 – 20.5-mm). The mean ± SD for D-MD was 9.12-mm ± 1.51 (range = 6.0 – 12.0-mm). The mean ± SD for D-FL was 5.94-mm ± 0.72 (range = 4.0 – 7.0-mm). The mean ± SD for D-O was 7.53-mm ± 0.98 (range = 5.25 – 9.5-mm). In general, the D-MD was larger than D-FL and H was larger than D.

Preparation Height/Diameter Ratio

The mean ± SD for H/D-MD was 1.26 ± 0.41 (range = 0.52 – 2.13). The mean ± SD for H/D-FL was 1.91 ± 0.59 (range = 1.08 – 3.15). The mean ± SD H/D for the entire preparation (H/D-O) was 1.59 ± 0.46 (range = 0.80 – 2.51).

Table 2 shows the distribution of preparations between two categories (H/D < 0.0, H/D > 1.0). An H/D of 1.0 was chosen as a cut-off point because any H/D > 1.0 theoretically has no CA_lim and thus would always have resistance form, regardless of CA. Considering H/D-MD only, 23/32 (71 %) were > 1.0. Considering only H/D-FL, 32/32 (100 %) were > 1.0. When H/D-O was considered, 28/32 (87.5 %) were > 1.0.

Table 2.

Percentage of preparations with height/diamaeter ratio (H/D) above and below 1.0.

	H/D Ratio
	< 1.0	> 1.0
H/D-MD	29.0%	71.0%
H/D-FL	0%	100%
H/D-O	12.5%	87.5%

MD = mesiodistal; FL = faciolingual; O = overall

Upon evaluation of the data, a significant association between H/D and CA was seen (MD: ρ = −0.76, FL: ρ = −0.62, O: ρ = −0.8). As H/D increased, CA decreased and approached what has been traditionally considered ideal (Fig. 7).

Figure 7.

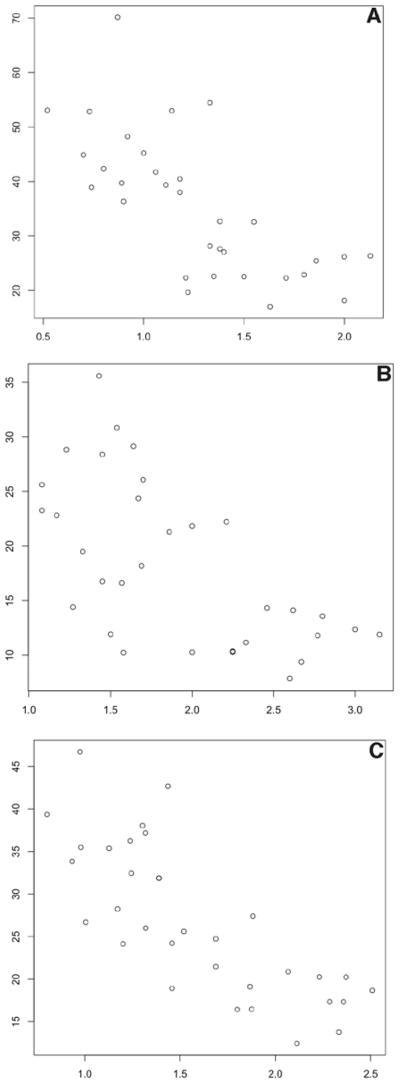
Histograms depicting the relationship between height/diameter (H/D) and convergence angle (CA) for mesial-distal (A), facial-lingual (B), and overall (C) measurements. H/D is plotted on the x axis and CA (in degrees) is plotted on the y axis.

Limiting Average Convergence Angle

Considering the MD measurements, 9/32 (28.13 %) of preparations had a calculable CA_lim. If only the FL measurements were considered, this number dropped to 0/32 (0.00 %). When the overall preparation was taken into consideration, 4/32 (12.5 %) of preparations had a calculable CA_lim.

When considering only the MD measurements, 28/32 (87.5 %) of the preparations had a CA below the corresponding CA_lim. When considering only the faciolingual measurements, 32/32 (100 %) of the preparations had a CA below the corresponding CA_lim. When considering the overall preparation, 32/32 (100 %) of the preparations had a CA below the corresponding CA_lim.

Clinical Outcome

Of the 32 medical records reviewed, one patient was lost to follow up. Of the patients that required follow-up by phone communication, none had a restoration failure, as indicated by the client confirming that the restoration was present. The mean ± SD for follow-up time was 3.59 ± 1.63 yrs (range = 1.5 – 7 yrs). Three restorations (3/31, 9.67 %) were lost because of an adhesive/cohesive failure and three (3/31, 9.67 %) were lost because of a tooth fracture. When considering all sources of failure, the clinical failure rate was 6/31 (19.35 %).

Association Between CA and Clinical Outcome

Restorations that failed via adhesive/cohesive failure had numerically higher mean ± SD CA’s (CA-MD: 50.62° ± 1.02; CA-FL: 25.34° ± 2.54; CA-O: 37.98° ± 1.78) than those that failed via tooth fracture (CA-MD: 28.38° ± 1.13; CA-FL: 18.58° ± 0.62; CA-O: 23.46° ± 0.87) and those that did not fail (CA-MD: 34.42° ± 2.16; CA-FL: 17.74° ± 1.46; CA-O: 25.72° ± 1.81) (Table 3). However, this association was not statistically significant. (CA-MD: P = 0.07, CA-FL: P = 0.26, CA-O: P = 0.06).

Table 3.

Convergence angle (CA) according to clinical outcome.

	Adhesive/Cohesive Failure	Non-Failure	Tooth Fracture Failure
CA-MD	50.62 1.02	34.42 2.16	28.38 1.13
CA-FL	25.34 2.54	17.74 1.46	18.53 0.62
CA-O	37.98 1.78	25.72 1.81	23.46 0.87

^*= mean SD; MD = mesiodistal; FL = faciolingual; O = overall; MD= mesiodistal; FL = faciolingual; O = overall

Association Between H/D and Clinical Outcome

In general, restorations that failed via an adhesive/cohesive failure had a numerically lower mean ± SD H/D (CA-MD: 0.92 ± 0.16; CA-FL: 1.4 ± 0.29; CA-O: 1.16 ± 0.2) than both non-failures (CA-MD: 1.29 ± 0.41; CA-FL: 1.96 ± 0.61; CA-O: 1.6 ± 0.5) and restorations that failed from tooth fracture (CA-MD: 1.49 ± 0.46; CA-FL: 2.11 ± 0.51; CA-O: 1.8 ± 0.48) (Fig. 8). Restorations that failed from tooth fracture had a higher mean H/D than those that did not fail and those that failed from adhesive/cohesive failure (Table 4). However, neither of these associations were statistically significant (H/D-MD: P = 0.22, H/D-FL: P = 0.26, H/D-O: P = 0.23).

Figure 8.

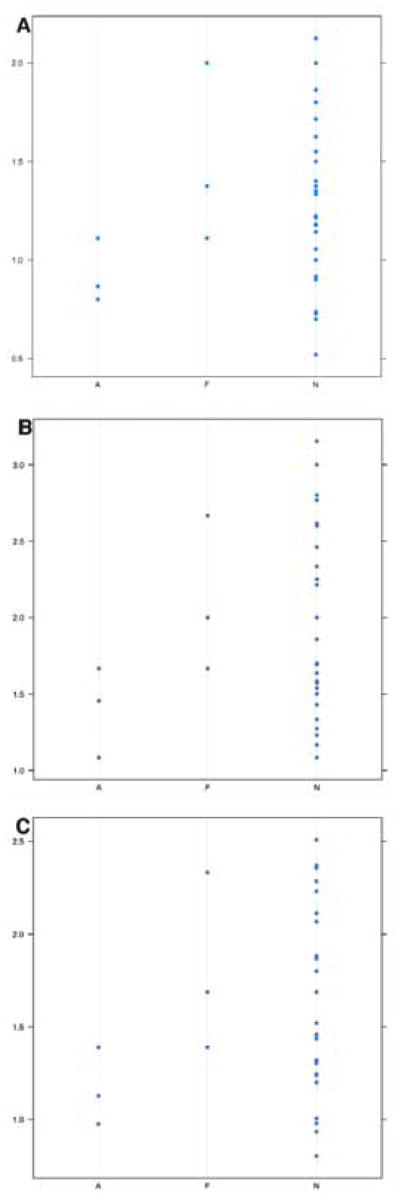
Dotplots depicting the association between height/diameter (H/D) and clinical outcome for mesial-distal (A), facial-lingual (B), and overall diameter (C) measurements. Clinical outcome (A = adhesive/cohesive failure, F = fracture failure, N = non-failure) is plotted on the x axis and H/D is plotted on the y axis.

Table 4.

Preparation height/diameter ratio* (H/D) according to clinical outcome.

	Adhesive/Cohesive Failure	Non-Failure	Tooth Fracture Failure
H/D-MD	1.40 0.16	1.96 0.41	2.11 0.45
H/D-FL	0.92 0.29	1.29 0.61	1.49 0.51
H/D-O	1.16 0.20	1.63 0.50	1.80 0.48

^*= mean SD; MD = mesiodistal; FL = faciolingual; O = overall; MD = mesiodistal; FL = faciolingual; O = overall

Association Between CA_lim and Clinical Outcome

The number of adhesive/cohesive failures with a CA that exceeded the CA_lim was numerically higher (1/3; 33.33 %) than the number of both fracture failures (0/3; 0 %) and non-failures (3/25; 12 %) with a CA that exceeded CA_lim (Fig 9). However, this association was not statistically significant (CA_lim-MD: P = 0.66, CA_lim-FL: P = 0.9, CA_lim-O: P = 0.9).

Figure 9.

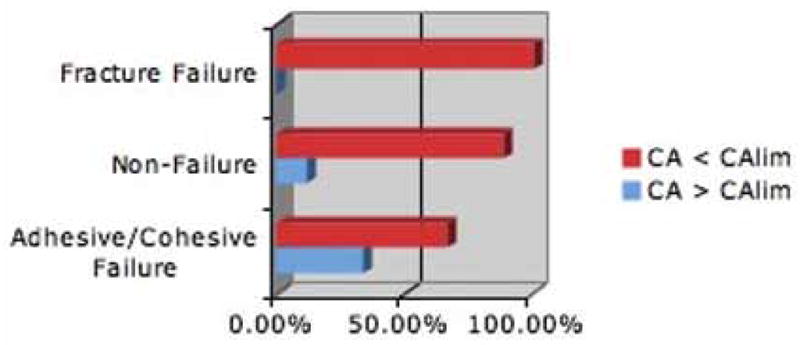
Bar graph depicting clinical outcome and the association between (% preparations) those preparations in which the convergence angle (CA) either exceeded the limiting CA (CA_lim) or did not exceed the corresponding CA_lim.

Discussion

A review of the literature on the subject of inclination of clinical crown preparations reveals a frustrating reality based on the inappropriate and synonymous use of the terms taper and convergence angle leading to inevitable confusion. One must always pay close attention to how authors define these terms. Most authors define taper and convergence angle as we have defined them within this manuscript. In this manuscript, every effort to distinguish between the two terms has been done when possible. However, in some cases, authors are not explicit in how they define taper and convergence angle. For example, some authors use the term taper to describe what most authors define as convergence angle.^1,6,8 Others use the term taper without clearly defining its meaning.⁵ Thus, the reader could interpret a recommendation of a 5 – 7° taper as meaning anything between 5° and 14°. When possible, we have substituted convergence angle for taper when referencing these authors to increase the readers ability to easily compare previously reported angles with those reported in this study.

Evidence-based clinical guidelines for full veneer restorations have not been clearly established in the veterinary literature. Indeed, the veterinary literature regarding prosthodontic treatment in companion animals is sparse and consists primarily of case reports and guidelines based on human research.^4,5,9–12 An early description of crown therapy in dogs recommends the divergence of a single axial wall not exceed 3° (or a 6° CA).⁹ Another veterinary dentist has recommended a 10° convergence angle.¹⁰ Otherwise, references simply state that near parallelism should be attempted,^4,5,11,12 with one author describing a “stair-stepping” preparation to aid in achieving parallelism.⁴ Others admit that although a 5–7° taper is recommended, this cannot be achieved in the canine tooth of the dog without major structural reduction.⁵ This would suggest that the “stair-stepping” technique might be contraindicated.

The earliest work evaluating the relationship between convergence angle and retention/resistance, and thus, the current recommendation, was performed in 1955.¹³ Prior to this work it had been generally accepted that retention of a crown would increase as the convergence angle decreased. In an in vitro study, the authors showed that if a tensile force was applied, the amount of force required to separate the restoration would drop as the convergence angle increased. This relationship was found to be hyperbolic with a precipitous drop in retention as the convergence angle increased from 5° to 20° with a plateau in retention between 20° and 90°.¹³ These findings were confirmed in subsequent in vitro studies.^14,15

Despite the in vitro data that supports a low convergence angle, several studies in humans have shown that such a low convergence angle can rarely be achieved clinically.^7,8,16–19 The mean mesiodistal and faciolingual convergence angles of stone dies prepared by dental students were evaluated with a reported range between 12.8° and 23.0°.¹⁶ Mean mesiodistal convergence angles of 16° and 24° for maxillary and mandibular full crowns, respectively were reported. For the faciolingual convergence angle, 20.7° and 20.3° were reported for maxillary and mandibular teeth, respectively. The overall preparation means were found to be 18.4° and 22.2° for maxillary and mandibular full crowns, respectively.⁷ Others have reported mean convergence angles that were similar to previous studies.⁸ The mean mesiodistal and faciolingual angles were found to be 20.3° and 18.3°, respectively. In a prospective study, a group of participants were advised to attempt a 4–10° convergence angle.¹⁷ The average mesiodistal convergence angles achieved for anterior and premolar regions were 16.05° and 16.8°, respectively. The average faciolingual convergence angles were determined to be 21.05° and 16.15° respectively for the anterior and premolar regions. Another study reported a mean convergence angle between 15° and 19°, while another showed a mean convergence angle ranging between 15° and 27° depending on the experience of the clinician.^18,19 The present study reveals a pattern of higher CA’s than the established ideal similar to that reported in humans. The CA ranged between 7.86° and 70.14°, with the lowest value measured in the CA-FL orientation and the highest value measured in the CA-MD orientation. This range is much broader than that reported in humans. In addition, the CA-FL in humans is typically larger than the CA-MD. We found the opposite to be true for the canine tooth in dogs (mean CA-MD = 35.5°; mean CA-FL = 18.48°). These differences likely reflect anatomical differences between human and dog teeth and differences in how the tooth presents for restoration in humans compared to dogs. The natural CA between the mesial and distal axial walls is quite large in dogs due to the distal curvature of the tooth. The natural CA between the facial and lingual axial walls approaches parallelism. Human teeth tend to be more columnar or cuboidal in shape, which allows a better chance at achieving parallelism. Full veneer restoration in human teeth is typically performed secondary to decay, which may not cause significant variation in tooth height. However, dogs receive full veneer restoration either secondary to dentoalveolar trauma and distal abrasion, or subsequent to endodontic therapy of an intact, non-vital tooth. Intact and abraded teeth usually do not have any significant reduction in height, whereas fractured teeth have variable degrees of height reduction. Due to the curvature and the associated steep inclination of the cervical region of the distal aspect of the canine tooth in dogs, fractured teeth have a higher natural CA compared to intact and abraded teeth.

If consideration was given to only the mesiodistal or faciolingual axial wall of human teeth, the ideal convergence angle was achieved only 5.3 % of the time.¹⁸ If both axial walls were considered together, this figure dropped to 0.4 %. When considering the faciolingual axial walls, 13 % of preparations fell within the recommended convergence angle range, while only 3 % of mesiodistal axial wall preparations fell within the recommended range. Our study revealed that when considering only the CA-FL, more preparations (31.25 %) were within the recommended range. However, the forces that canine teeth are exposed to are typically in a mesiodistal oblique direction. Therefore, the convergence angle that would be of most clinical interest would be CA-MD. Considering only the CA-MD, 0% were within the recommended range (< 12.0°), which is closer to what has been reported in humans. In addition, when considering only the CA-MD, 75 % of the preparations had a CA > 25°. Taking the entire preparation into consideration, 0 % fell within the recommended range.

There is a linear regression relationship between achievable convergence angle and height of clinical preparations.⁶ As the preparation height decreased, the clinically achieved convergence angle increased. It was presumed that a lower tooth height made it more difficult for the operator to visually maintain the bur at the appropriate angle. The present study reveals a similar pattern. This relationship is the reverse of what is clinically desired. As the preparation height decreases, achieving a low convergence angle becomes even more important to maintain retention/resistance. However, due to the naturally steep inclination of the cervical distal axial wall of the canine tooth, achieving a lower convergence angle in this region becomes extremely difficult, if not impossible.

Most studies evaluating the effect of convergence angle on retention/resistance are in vitro studies. To our knowledge, this is the first study that has attempted to evaluate the role of the clinically achieved convergence angle in clinical outcome of the restoration. Although not statistically significant, our study showed that restorations that failed via adhesive/cohesive failure had numerically higher mean CA’s than those that failed via tooth fracture and those that did not fail (Table 3). This was expected given the enormity of in vitro data that supports this association.

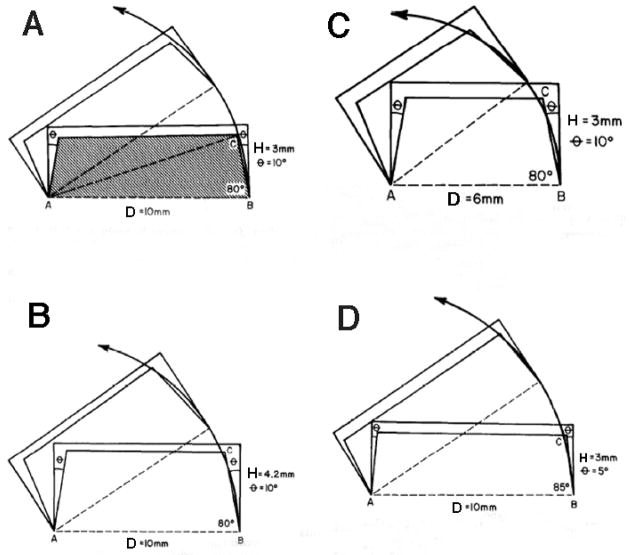
Convergence angle is only one of many factors influencing retention/resistance form. The height and base diameter of the preparation are also important factors. It has been shown that for a given base diameter and convergence angle, an increase in height results in increased retention.¹⁴ The roles of height, base diameter, and convergence angle in preventing restoration dislodgement have been evaluated.³ For a given tooth diameter and convergence angle, preparation height is directly proportional to dislodgement resistance (Fig. 10). Conversely, for a given height and diameter, convergence angle is inversely proportional to dislodgement resistance. The present study suggests that this is also true for the canine tooth in dogs. Although not statistically significant, those restorations that proved not to have adequate retention/resistance (indicated by an adhesive/cohesive failure) generally had a lower H/D, compared to those that did not fail and those that failed via fracture (Table 4; Fig. 8).

Figure 10.

Figures depicting the interdependent relationship between preparation height, preparation base diameter, and convergence angle (CA). (A) If for a given diameter (10-mm), convergence angle (10), and height (3-mm), line AB is equal to or longer than line AC, casting will dislodge. (B) If height is increased from 3 to 4.2-mm, casting will not dislodge because of interference with side BC. (C) If diameter is decreased from 10 to 6-mm, casting will not dislodge because of interference with side BC. (D) If convergence angle is reduced from 10 to 5, casting will not dislodge because of interference with side BC.

(Modified with permission from Weed RM, Baez RJ. A method for determining adequate resistance form of complete cast crown preparations. J Prosthet Dent 1984; 52:330–334.3)

After evaluation of the inter-dependant relationship between the physical properties of a preparation and retention/resistance, the concept of limiting average taper (T_lim) was developed.² This concept allowed the authors to provide, for any given H/D ratio, a limiting taper at which any taper above this value does not have resistance form and any taper below this value does have resistance form. Based on the formula presented previously, any ratio > 1.0 always has resistance form regardless of taper. In the present study, we modified this formula to use convergence angle, rather than taper, to allow a direct comparison between CA and CA_lim. The present study suggested an association between CA_lim and clinical outcome. Those preparations with a CA that exceeded CA_lim were 2.7 times more likely to suffer an adhesive/cohesive failure compared to those that did not have a CA that exceeded the CA_lim.

Early studies evaluating the effect of convergence angle on resistance/retention form were based on the use of zinc phosphate cement. Newer resin-based cements have since been developed and have been shown to provide greater retentive force compared to zinc phosphate cements.^20–23 Studies have also shown that the type of cement used plays a pivotal role in the relationship between convergence angle, height, and the retentive force of the restoration.^24,25 It has been shown that a restoration cemented with a resin-based cement onto a preparation with 35° taper had higher retention compared to a restoration cemented with zinc phosphate onto a preparation with 12° taper.²⁴ Further, if the taper remained constant and the crown height was increased, preparations cemented with resin-based cements had higher retention values compared to preparations cemented with zinc phosphate cements. It was concluded that preparations with tapers greater than 12° should be cemented with resin-based cements to improve retention and clinical success.²⁵ All restorations in this study were cemented with the same resin-based cement. Despite the high mean CA found in our study, the success rate compares to those reported in the literature regarding humans.²⁶ Although we did not evaluate the effect of the cement on the clinical outcome in this study, it is likely that the high success rate of full veneer crowns of canine teeth in dogs is due at least in part to the excellent bonding properties of resin-based cements.

Our overall clinical failure was 6/31 (19.35 %). In the present study, we considered an adhesive/cohesive failure representative of inadequate retention/resistance form. Three (3/31; 9.67 %) were considered adhesive/cohesive failures and 3 (9.67 %) were considered tooth fracture failures. This is comparable to a previous report of the clinical performance of metal crowns in a group of 18 working dogs, which reported an overall clinical failure rate of 12.2 % (5/41); one (2.4 %) of which was considered an adhesive/cohesive failure and 4 (9.8 %) of which were considered fracture failure.²⁷ The higher failure rate reported in the present study may reflect the follow-up time. Survivability of a restoration is time-dependent. Studies in humans reveal a steady decline in survivability with increased follow-up time.²⁶ The mean follow-up time for the previous study²⁷ was 2.83 yrs, compared to 3.59 yrs for this study. It is likely that the success rate would further decline with increased follow-up time.

The retrospective nature of this study presents several limitations. The most significant limitation was the population size. The low clinical failure rate of full veneer restorations of the studied population presented challenges the statistically significant associations between the physical properties of the preparation and clinical outcome. Assuming a failure rate consistent with that determined within this study, a power analysis reveals a necessary population size of approximately 300 total cases to ensure statistically significant data. Larger, multi-institutional studies are indicated to fully evaluate the potential associations investigated in this study.

The data presented here does suggest an association between physical properties of a preparation and the clinical outcome: preparations with a high CA are more likely to not have retention/resistance form; successful restorations can have a CA higher than that which is recommended; preparations with a high H/D are more likely to have retention/resistance form but also more likely to fracture; the chance of adhesive/cohesive failure may be higher if the CA exceeds the calculated CA_lim. These findings support, but do not confirm in a statistically significant manner, our original hypotheses. We believe that, based on this study, the following clinical recommendations can be made: 1) an ideal CA (12.0°) can rarely be achieved for the canine tooth in the dog. However, a CA exceeding 12.0° is usually acceptable for resistance/retention. 2) the more clinical crown available (high H/D), the less concerned the veterinary dentist needs to be with the CA. Achieving a low CA becomes most important as the H/D decreases. 3) in light of the high CA shown in this study, a resin-based cement is always recommended. 4) as the H/D increases, the chance of a tooth fracturing post-treatment may increase. 5) the CA_lim can be used as a guide for determining the necessary CA for retention/resistance according to the formula CA_lim = arcsin (H/D).