ESTIMATING WITHIN-HOUSEHOLD CONTACT NETWORKS FROM EGOCENTRIC DATA

Abstract

Acute respiratory diseases are transmitted over networks of social contacts. Large-scale simulation models are used to predict epidemic dynamics and evaluate the impact of various interventions, but the contact behavior in these models is based on simplistic and strong assumptions which are not informed by survey data. These assumptions are also used for estimating transmission measures such as the basic reproductive number and secondary attack rates. Development of methodology to infer contact networks from survey data could improve these models and estimation methods. We contribute to this area by developing a model of within-household social contacts and using it to analyze the Belgian POLYMOD data set, which contains detailed diaries of social contacts in a 24-hour period. We model dependency in contact behavior through a latent variable indicating which household members are at home. We estimate age-specific probabilities of being at home and age-specific probabilities of contact conditional on two members being at home. Our results differ from the standard random mixing assumption. In addition, we find that the probability that all members contact each other on a given day is fairly low: 0.49 for households with two 0–5 year olds and two 19–35 year olds, and 0.36 for households with two 12–18 year olds and two 36+ year olds. We find higher contact rates in households with 2–3 members, helping explain the higher influenza secondary attack rates found in households of this size.

1. Introduction

Acute infectious diseases such as influenza are spread over networks of social contacts. The 2009 pandemic influenza A (H1N1) virus has spread to 214 countries and caused over 18,000 deaths (WHO, 2010), and a global avian influenza pandemic continues to pose a real and dangerous threat. Large-scale simulation models are used to predict the spread of the epidemic and evaluate intervention strategies, but these models are based on simplistic and strong assumptions about human interactions. (See Halloran et al (2008), Germann et al (2006), and Ferguson et al (2006).) For example, they assume random mixing within homes, schools, workplaces, and communities, but these social network patterns are not estimated from surveys of contact behavior. Eubank et al (2004) implement a more detailed agent-based simulation model based on transportation data and activity surveys, but again the model is not informed by contact surveys. As Mossong et al (2008) stated in their analysis of the data motivating our methods, “Researchers often rely on a priori contact assumptions with little or no empirical basis.”

These basic assumptions are also used in estimating key transmission parameters. One such parameter is the basic reproductive number (R₀), the expected number of secondary infections generated by a single infectious individual in a completely susceptible population (Anderson and May, 1991). Estimating R₀ for acute infectious diseases commonly assumes random contacts by age group. Goeyvaerts et al (2009) and Wallinga, Teunis, and Kretschmar (2006) use contact data to inform the age-based contact rates used to estimate R₀, but other network structures are not taken into account. Davoudi et al (2009) took a new and important step by incorporating the degree distribution in their estimation of R₀ for influenza, where the degree is the number of contacts each person makes. Random mixing within households is also assumed when estimating secondary attack rates within households – for example in Longini et al (1988), Halloran et al (2006), and Yang, Longini, and Halloran (2007). Britton and O’Neill (2002) assume random mixing in their Bayesian method to estimate the mean of the infectious period, the infection rate, and the probability of social contact. Demeris and ONeill (2005) develop a Bayesian method which imputes the graph of contacts between individuals from final outcome data. They assume random mixing (within group and between group) and separate within-group and between-group infection rates.

Network structures such as clustering, transitivity, and variation in degree are known to play a role in disease transmission (e.g. Hethcote (1984), Miller (2009), and Keeling and Eames (2005)). However, the impact of these structures on transmission models is still an open area of exploration. We can improve existing influenza simulation models by collecting survey data on social contact behavior, developing methodology to infer the contact network from survey data, assessing the impact of network structures on disease spread, and finally, integrating the important structures into the simulation models. Parameter estimation procedures can be improved by the same process.

We contribute to the second step in this process by developing a parametric model to estimate within-household contact networks from diaries of social contacts and analyzing the POLYMOD data from Belgium. In the diaries respondents reported on their contacts to other household members, but not on contacts between other members. This network sampling design is called egocentric. Egocentric data includes information on respondents and people contacted, as well as numbers and characteristics of contacts, but the identities of the people contacted are not collected. With such data, the probability distribution of the entire network may be inferred if we assume that the probability of contact depends only on individual-level attributes, or if explicit assumptions regarding dependence are made. We take the latter approach in this paper. Koehly, Goodreau, and Morris (2004) discuss the use of conditional log-linear models to analyze egocentric data. Handcock and Gile (2007, 2010) develop a conceptual framework for inference of network parameters from sampled data under a variety of sampling designs. As egocentric data is commonly and easily collected from networks, our work is applicable to network inference in other settings.

A number of dependencies may exist in the contact network. For example, transitivity may be present: that is, if two household members contact the same third member, they are more likely to contact each other. Our observed egocentric data contain limited information about dependencies in contact behavior: for example, they do not contain information about transitivity. However, our data set includes a household age roster for each respondent, so some information on dependency is available. We observed that some respondents contact no household members, but those who contact any household members are likely to contact all or most of them. Thus, the raw data suggest that if a respondent contacts at least one household member, then the probability of contacting other members is increased. We hypothesize that some respondents were away from home on the day they filled out the contact diary (which was mailed to them in advance). We model a latent variable indicating which household members are at home on a given day, thus building dependency into our network. We assume that no contacts occur to household members who are away from home on a given day. We estimate age-specific probabilities of being at home as well as age-specific probabilities of contact conditional on both household members being at home. We test whether contact behavior differs on weekdays versus weekends, during the Easter holiday period versus the non-holiday period, and in small (< 4) versus large (≥ 4) households. We prove identifiability of our model and use simulated data to assess conditions for weak identifiability.

2. Data

Our data comes from the POLYMOD study, a survey in eight European countries of social contact behavior. Mossong et al (2008) perform descriptive analyses of this data set and analyze mixing patterns by age. We use the Belgian data, which was collected from 750 respondents during March-May 2006. Hens et al (2009) perform a detailed analysis of the Belgian POLYMOD data using association rules and classification trees. Participants were recruited by random digit dialing on fixed telephone lines. Respondents were selected to represent the urban/rural divide in Belgium and the populations of the three main regions (Flemish, Walloon, and Brussels). Children were oversampled as they play an important role in infectious disease spread. By design, 10% of the sample falls in each of the child age groups (0–4, 5–9, 10–14, and 15–19) and 6% in each of the adult age groups (20–24, 25–29, 30–34, 35–39, 40–44, 45–49, 50–54, 55–59, 60–64, 65+). Survey participants were assigned two randomly selected days (one weekday and one weekend day) and were asked to record their social contacts between 5 a.m. and 5 a.m. the following morning. Each received a paper diary and recorded sociodemographic information of self and household, and characteristics of all contacts made during the day. A contact was defined to be either a physical contact or a two-way conversation of at least three words in the physical presence of another person. Age and sex of the person contacted were recorded, but no other identifying information on the contacted individual was collected.

Respondents did not record whether contacted individuals were household members or not. However, they did record the ages of all household members in the demographic section of the survey. In addition, respondents recorded age and sex of each person contacted, recorded frequency of contact with that person, and checked off all locations where that person was contacted on the day of the survey (home, work, school, transport, leisure, and/or other). We assume that contacts which occurred “at home”, were reported as “daily or almost daily”, and whose age matches one of the reported ages of household members, were indeed contacts to that member. For each household we observe a partial contact network: we have information on ties between the respondent and all other members, but not on contacts between other members. By design, only one respondent per household was surveyed.

Participants also recorded the date of the diary. Roughly half of respondents (381 of 750) filled out the first day of their diary during the two-week Easter holiday period (April 3–17), during which schools were closed. Nearly three quarters (545 of 750) filled out the second day of their diary during this holiday period, and over half (365 of 750) filled out both days during the holiday period.

Table 1 shows the household size distribution of our data set. Most households are size 2, 3, or 4. To give the reader a sense of the diversity in age composition in the data set, we display the age composition distribution in Table 2 for households of size four only. We have divided survey respondents and their household members into the following five categories: 0–5, 6–11, 12–18, 19–35, and 36+, because we believe these age groups are likely to exhibit different contact behavior. For example, 0–5 year olds are not yet in school in Belgium and require high levels of contact with their parents, 6–11 year olds are in primary school, and teenagers are even more independent than 6–11 year olds so may spend less time at home, etc. Note that some age compositions are represented by only one or two respondents in the survey. Of course, additional age compositions exist in the data set for households with sizes other than four, so there is a great deal of diversity. As we are modeling household contact networks, we restrict our attention to respondents in households with two or more members (n=675).

Table 1.

Household size distribution in the POLYMOD data from Belgium

Household size	1	2	3	4	5	6	7	9	12
Number of observations	75	157	195	213	83	23	2	2	1

Table 2.

Age composition of households of size four in the Belgian POLYMOD survey. Each row depicts a specific age composition by showing the number of members in each age category. The rightmost column of the table shows the number of respondents in households of that age composition in the POLYMOD study in Belgium.

Age Category					Number of Respondents
0–5	6–11	12–18	19–35	36+
0	0	0	0	4	1
0	0	0	1	3	1
0	0	0	2	2	35
0	0	0	3	1	1
0	0	0	4	0	1
0	0	1	1	2	23
0	0	1	2	1	1
0	0	2	0	2	40
0	0	3	0	1	2
0	1	0	0	3	1
0	1	0	1	2	1
0	1	1	1	1	2
0	1	2	0	1	1
0	1	1	0	2	17
0	1	2	0	1	1
0	2	0	0	2	16
0	2	0	1	1	8
0	2	0	2	0	4
1	0	1	0	2	1
1	1	0	0	2	6
1	1	0	1	1	8
1	1	0	2	0	12
2	0	0	0	2	2
2	0	0	1	1	12
2	0	0	2	0	16

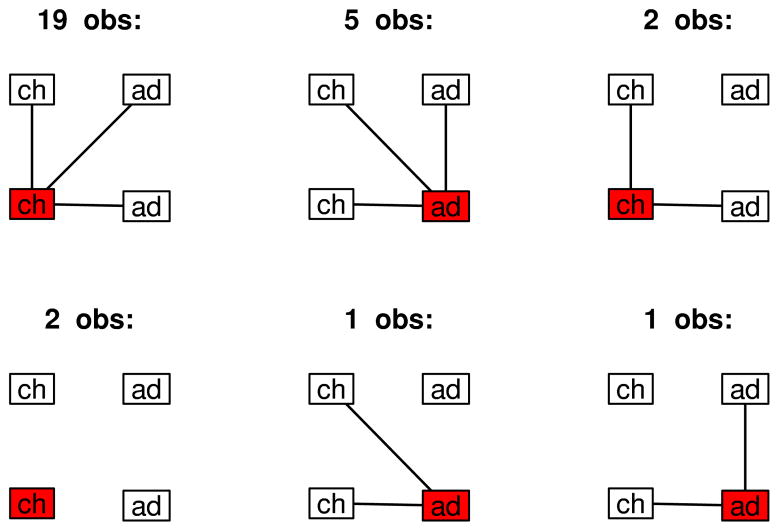
Figure 1 shows a subset of the data: households of size four with two 0–5 year olds and two 19–59 year olds. We have marked the respondent in red. For display purposes we have assumed the two children are exchangeable and the two adults are exchangeable. Child respondents are likely to report making all three possible contacts, and adult respondents are also likely to report having contacted all three other household members. The next most likely report is two out of three contacts. Finally, two child respondents reported contacting no one. This seems strange as the children are 0–5 years old, but we hypothesize that they were not at home on the day of the survey. The paper diary mailed to respondents could be filled out anywhere, and a parent or other guardian filled out the survey for child respondents. We examined several types of household age compositions and always found a subset of respondents to report no household contacts. Overall, 16% of respondents report no household contacts, yet those who report at least one contact contacted an average of 88% of their household members. This suggests a dependency in contact behavior: if at least one household member is contacted, then others are more likely to be contacted.

Fig 1.

Subset of observed data: households with two 0–5 year olds and two 19–59 year olds; respondent in red. Lines indicate reported contact.

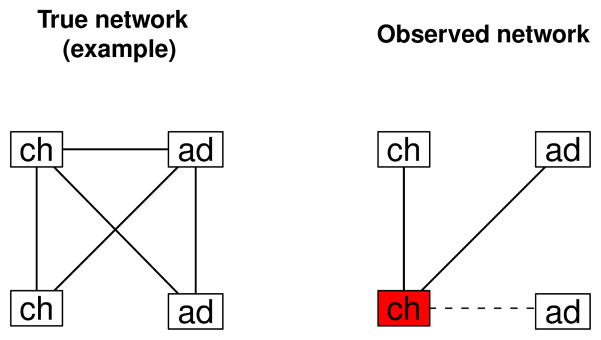
Figure 2 shows an example of how the observed data compare to the true, complete network. We develop a model to infer the probability distribution of the complete network, based on partial observations of the network.

Fig 2.

Example of a true network and the observed portion from the POLYMOD study. In the plot of the observed portion, the respondent is red, solid lines indicate observed contacts, and the dashed line shows the observed non-contact.

3. Methods

In this section we present a model for the contact network and develop inference for it based on the incomplete information available in the egocentric data. The model for the contact network is of primary scientific interest.

3.1. A Latent Variable Model

Our inspection of the observed data revealed that some respondents reported no “at home” contacts to other household members on the day of the survey. This may occur because the respondent was not actually at home on the day of the survey, or because he/she was at home but made no social contacts at home. Our data do not directly distinguish between a respondent being away from home versus being at home but not contacting any household members. We use a latent variable model to tease apart these two phenomena.

For a household of size k, let Z denote a random matrix representing the at home contact network. We represent Z by a k by k sociomatrix, where

$$Z_{ij}=\{\begin{array}{ll}1\hfill & \text{if}\text{there}\text{is}\text{a}\text{contact}\text{between}\text{person}\text{i}\text{and}\text{person}\text{j},\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

Let H be a Bernoulli random vector of length k, indicating whether each household member is home or not. We assume that the elements of H are independent; that is, the absence of one household member does not influence whether another household member is also absent. If H is unobserved, we can express the likelihood of Z by the Law of Total Probability as follows:

$$P(\mathbf{Z}=\mathbf{z})=\sum _{\mathbf{h}\in \mathcal{H}}P(\mathbf{Z}=\mathbf{z}\mid \mathbf{H}=\mathbf{h})P(\mathbf{H}=\mathbf{h})$$ (3.1)

Above, 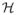represents the space of all possible “at home” vectors H. We now add some assumptions about the distributions of H and Z|H.

We assume that H_i ~ Bernoulli(p_v), where v is the age category of house-hold member i. We parametrize the distribution of Z|H by assuming that contacts Z_ij|(H_i = 1, H_j = 1) are independent Bernoulli random variables whose probability parameters depend only on the age categories of house-hold members i and j. We define p_rs as the probability of contact between a member of age category r with a member of age category s, conditional on both of them being at home. So Z_ij|(H_i = 1, H_j = 1) ~ Bern(p_rs), where r is the age category of member i and s is the age category of member j. We assume contacts are symmetric, so p_rs = p_sr. We will model only at-home contacts between household members, so Z_ij is zero when either H_i = 0 or H_j = 0. Thus, we assume that the only dependence in contacts between members comes from whether the members are at home or not.

The Bernoulli assumptions allow us to collapse contacts into counts by age groups. Although our outcome of interest is the sociomatrix, we observe only a single row of the sociomatrix for each household. Under our model assumptions, a sufficient statistic for the contribution of each household is a vector W, with elements W_s = the number of contacts observed from the respondent to household members in age group s, for s ∈ {1, …, 5}. Let n = (n₁, n₂, n₃, n₄, n₅) denote the number of non-respondent household members in each age category. Then n_s − W_s is the number of members in age category s who were not contacted by the respondent.

With a slight abuse of notation we will still use H to denote home/away status, but the elements will be counts rather than indicators. Now let H_v be the number of non-respondent household members in age category v who are at home rather than the home/away status of member v. The new H has length 5 regardless of household size. Then H_v follow independent binomial distributions with parameters n_v and p_v, where n_v is the number of non-respondent household members in age category v, and p_v is the probability of a person in age category v being at home. In addition, let R denote the home/away status of the respondent, with R = 1 if the respondent is home, and R = 0 otherwise. Since respondents were mailed a paper diary in advance of their survey date and returned it by mail, and since some respondents did not list any household contacts in their diary, the “at home” status of the respondent is unobserved. The latent variables of interest are H and R.

Under these assumptions the likelihood contribution for a respondent in age category j is:

$$P(\mathbf{W}=\mathbf{w})=P(\mathbf{W}=\mathbf{w}\mid \text{R}=0)(1-p_j)+P(\mathbf{W}=\mathbf{w}\mid \text{R}=1)p_j$$ (3.2)

Above, P(W = w|R=0) = 1 if w = (0, 0, 0, 0, 0) and zero if w_s > 0 for at least one s ∈ {1, 2, 3, 4, 5}. If the respondent is at home, it follows from our assumptions that contacts to other household members are independent, so we can rewrite the second term as follows:

$$P(\mathbf{W}=\mathbf{w}\mid \text{R}=1)p_j=\prod _{s=1}^{5}P(W_s=w_s\mid R=1)p_j$$ (3.3)

Household members who had reported contact with the respondent were necessarily at home. Those without reported contact could have been away from home, or could have been at home but not contacted. By applying the Law of Total Probability again, conditioning on the home/away status of non-respondent household members, (3.3) becomes:

$$p_j\sum _{h_1=0}^{n_1}\sum _{h_2=0}^{n_2}\cdots \sum _{h_5=0}^{n_5}\prod _{s=1}^{5}P(W_s=w_s\mid H_s=h_s)P(H_s=h_s)$$ (3.4)

By applying our distributional assumptions, this term becomes:

$$p_j\sum _{h_1=w_1}^{n_1}\sum _{h_2=w_2}^{n_2}\cdots \sum _{h_5=w_5}^{n_5}\prod _{s=1}^5\left(\begin{array}{l}{h}_s\hfill \\ w_s\hfill \end{array}\right)p_{js}^{w_s}{(1-p_{js})}^{h_s-w_s}\left(\begin{array}{l}{n}_s\hfill \\ h_s\hfill \end{array}\right)p_s^{h_s}{(1-p_s)}^{n_s-h_s}$$ (3.5)

We assume that households are independent, so the likelihood of the entire data set is the product of the likelihood contributions of all respondents. Note that the parameters n_s are determined by the data and differ for different respondents.

To aid in understanding, we provide an example for the reader.

Example 3.1

Suppose the respondent is in age group 1, and has two household members, one in age group 2, and one in age group 4, and suppose the respondent reports no contacts to household members on the day of the survey. Then, W = (0, 0, 0, 0, 0) ≡ 0 and n = (0, 1, 0, 1, 0). The likelihood contribution for this respondent is:

$$\begin{array}{l}P(\mathbf{W}=\mathbf{0})=P(\mathbf{W}=\mathbf{0}\mid \text{R}=0)(1-p_1)+P(\mathbf{W}=\mathbf{0}\mid \text{R}=1)p_1\\ =1-p_1+p_1(P(\mathbf{W}=\mathbf{0}\mid \mathbf{H}=\mathbf{0})P(\mathbf{H}=\mathbf{0})\\ +P(\mathbf{W}=\mathbf{0}\mid \mathbf{H}=(0,1,0,0,0))P(\mathbf{H}=(0,1,0,0,0))\\ +P(\mathbf{W}=\mathbf{0}\mid \mathbf{H}=(0,0,0,1,0))P(\mathbf{H}=(0,0,0,1,0))\\ +P(\mathbf{W}=\mathbf{0}\mid \mathbf{H}=(0,1,0,1,0))P(\mathbf{H}=(0,1,0,1,0)))\end{array}$$

by the Law of Total Probability, the independence of H and R, and the fact that P(W = 0|R=0) = 1. Next we apply the distributional assumptions on P(W|H) and P(H) to obtain

$$\begin{array}{l}=1-p_1+p_1\left((1-p_2)(1-p_4)+(1-p_{12})p_2(1-p_4)+(1-p_{14})(1-p_2)p_4+(1-p_{12})(1-p_{14})p_2{p}_4\right)\end{array}$$

Through algebra we can see that this is equivalent to (3.2).

3.2. Maximum Likelihood Estimation

By maximizing the likelihood we estimate the probability parameters p_rs and p_v for r, s, v ∈ {1, 2, 3, 4, 5}. We note that a Bayesian approach would also be appropriate for our question of interest, as we expect contact probabilities within households to be high, particularly when one of the members is a young child. We chose not to use a Bayesian approach because we prefer not to increase the subjectivity of our results.

Optimization was performed in R version 2.8 with the optimfunction. We used the BFGS method, a quasi-Newton method published simultaneously by Broyden, Fletcher, Goldfarb and Shanno (1970). The optim function estimates the Hessian of the log likelihood at the MLE, so providing an estimate of the observed Fisher information matrix which one can invert to compute confidence intervals. However, some parameter estimates were on the boundary of the parameter space, so we computed confidence intervals by a non-parametric bootstrap, as described by Efron and Tibshirani (1993), instead of by inverting the Fisher information matrix. We used 1,000 bootstrap iterations. In one case, both lower and upper bounds of the interval were estimated to be 1 since all data points supported a parameter estimate of 1. Since the bootstrap fails as an estimate of uncertainty in this case, we omit the lower bound of this interval. R code used for estimation is included in the supplementary material (Potter et al, 2011).

3.3. Identifiability of the Latent Variable Model

Since we are estimating a latent variable from a data set with structurally missing data, it is not immediately apparent that our parameters are identifiable. According to Silvey (1975), a parameter is identifiable if distinct values of the parameter vector give distinct probability distributions on the sample space. We prove identifiability of our parameter vector in the Appendix. It is possible that the identifiability is only “weak”. Identifiability guarantees that the parameter can be determined with an infinite amount of data, but “weak identifiability” means that even very large data sets do not contain enough information to precisely estimate the parameter (Bolker, 2008). Because we are using partially observed network data to estimate 20 parameters, five of which correspond to a latent variable, it is not immediately obvious that our data set is large and diverse enough to disentangle the “at home” probabilities from the conditional contact probabilities. We perform a simulation study to assess whether data sets with the same size and distribution of household age compositions as ours contain enough information to estimate our parameters.

3.4. Model Selection

We investigated three effects which could help to model contact behavior. First, contact probabilities may vary with household size, as people in large households may be less likely to contact all other members than those in small households. We also tested for differences during the Easter holiday and a non-holiday period, and between weekend days and weekdays. Because we are performing three statistical tests, we applied Bonferroni’s correction for multiple testing: we use a critical value of α = 0.05/3 = 0.017 instead of α = 0.05 (Abdi, 2007).

Let p_rs,small denote the conditional probability of contact between house-hold members in age groups r and s for households with 2–3 members, and p_rs,large denote the conditional probability of contact between household members in age groups r and s for households with four or more members. Similarly let p_s,small and p_s,large be the probabilities of a member in age category s being at home in small and large households. Let Ω₀ be the subspace in which we’ve restricted parameters for small households to be equal to those for large households: that is, p_rs,small = p_rs,large and p_s,small = p_s,large for r, s ∈ {1, 2, 3, 4, 5}. We are interested in testing whether p ∈ Ω₀ or p ∈ Ω\Ω₀. Because three of the parameter estimates are on the boundary of the space (p_0–5,0–5 = 1, p_{6–11,6–11} = 1 and p_{6–11,12–18} = 1), the conditions for the classical likelihood ratio test using Wilk’s (1938) theorem do not hold. However, when estimation was performed separately for small and large households, we found p_0–5,0–5 = 1, p_{6–11,6–11} = 1 and p_{6–11,12–18} = 1 for both small and large households. In both cases, there is not enough variability in the data to compute a confidence interval, suggesting that the true value is close to 1 for both small and large households. These parameters are estimated with sample sizes ranging from 29–34, and the data is consistent with a parameter value of 1. For this reason we considered it unnecessary to test for a household effect for these three parameters. Instead, we assumed that these three parameters were equal for small and large households, and tested whether any of the other 17 parameters differed for small versus large households. This permits us to do a classical likelihood ratio test, in which the test statistic is compared to a chi-square distribution with 17 degrees of freedom. Our test statistic was 37.4 with a p-value of 0.003, so we concluded that one or more of the parameters differs for small versus large households. While the estimated “at home” probabilities were similar for small and large households, nearly all conditional contact probability estimates were larger in small households than in large households. We chose not to include a household size effect in our final model, as some cell counts were too small to obtain reasonable estimates. The separate estimates for small and large households are included in the supplementary material (Potter et al, 2011).

We used the same method to assess whether contact behavior differed on the weekend versus on a weekday. Here, only one parameter estimate was on the boundary of the space. Our likelihood ratio test statistic was 23.3, which, when compared to a chi-square distribution with 19 degrees of freedom, gives a p-value of 0.22. Thus, we found no evidence that contact behavior differed over the weekend versus on a weekday.

Similarly, we tested the null hypothesis that the parameters were the same during the two-week Easter holiday period as during a non-holiday period against the alternative that one or more probability parameters could differ between the holiday and the non-holiday. Since our test statistic was 53.3 with a p-value < 0.001, we concluded that within-household contact behavior in Belgium is different during the Easter holiday period than during a non-holiday period. However, we did not see a systematic, meaningful, and substantive pattern explaining the difference. The separate holiday and non-holiday estimates are included in the supplementary material (Potter et al, 2011). For this reason, we chose not to include a holiday effect in our final model.

4. Results

4.1. Parameter Estimates

Table 3 shows maximum likelihood estimates for the probability of contact between two members, conditional on them both being at home. Table 4 shows estimates of the probability of members being at home on a given day. We see that contact probabilities are quite high from young children to all age groups, and decrease slightly as the ages of both members increase.

Table 3.

Conditional contact probability estimates with 95% bootstrap confidence intervals

Age Category	0–5	6–11	12–18	19–35	36+
0–5	1.00 [-, 1.00]	0.90 [0.76, 0.99]	0.67 [0.24, 0.99]	0.99 [0.93, 1.00]	0.96 [0.86, 1.00]
6–11		1.00 [0.86, 1.00]	1.00 [0.89, 1.00]	0.96 [0.88, 1.00]	0.91 [0.82, 0.98]
12–18			0.88 [0.74, 0.99]	0.65 [0.48, 0.81]	0.91 [0.85, 0.97]
19–35				0.80 [0.65, 0.94]	0.83 [0.75, 0.90]
36+					0.89 [0.81, 0.97]

Table 4.

Estimated probabilities of being at home with 95% bootstrap confidence intervals

Age Category	0–5	6–11	12–18	19–35	36+
Probability	0.90 [0.86, 0.95]	0.92 [0.88, 0.98]	0.89 [0.84, 0.94]	0.90 [0.86, 0.94]	0.92 [0.89, 0.95]

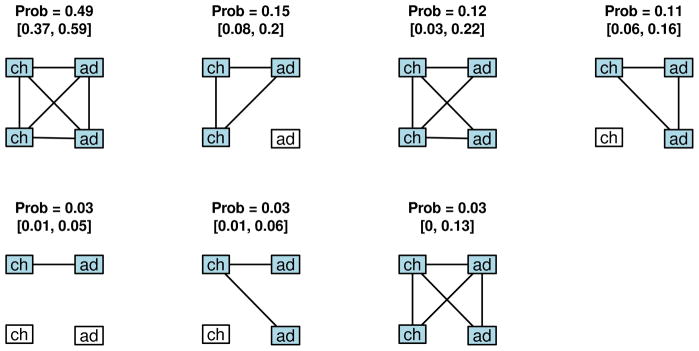
Our 20 parameters and our distributional assumptions determine the probability distribution of within-household contact networks for any household of a specified size and age composition. Figure 3 shows the estimated probability distribution of contact networks for households with two 0–5 year olds and two 19–35 year olds. The probability of the first network depicted is the probability that all household members are at home times the probability that all contacts between them occur. Other network probabilities are computed similarly. Confidence intervals were computed by performing this deterministic computation 1,000 times, using the parameter estimates obtained from the 1,000 bootstrap re-samples of our data set.

Fig 3.

Estimated probability distribution of contact networks, households with two 0–5 year olds and two 19–35 year olds, with 95% confidence intervals. Members at home are shown in blue; those away from home are shown in white. Only networks with probability >0.02 are depicted.

The “at-home” status of each member is indicated by color: blue members are at home and white members are away from home. According to our model, the most likely network includes all possible contacts, which fits with our understanding of social behavior. This network is estimated to have a 49% chance of occurring on a given day in this type of household. The second most likely network shows one of the adults away from home, but all other contacts occurring. The third most likely network, with probability 12%, has all members at home, and all contacts except the one between the two adults occurring.

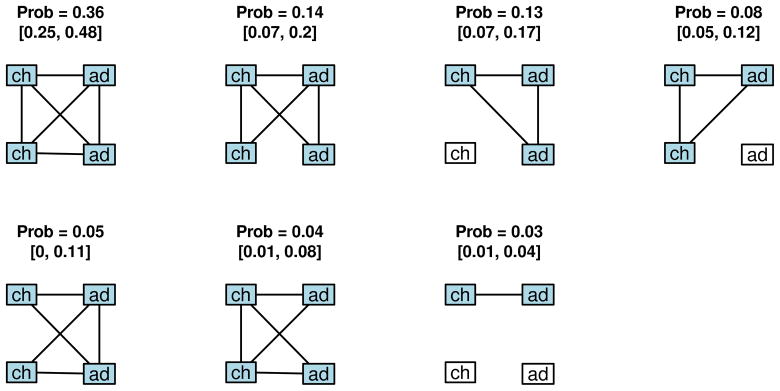
Figure 4 shows the estimated probability distribution for contact networks with two 12–18 and two 36+ year olds. As with the younger household type, the most likely network is the one in which all contacts occur, but its estimated probability is 0.36, rather than 0.49. As teenagers are more independent than children under 5, this seems reasonable. The second most likely network is one in which all members are at home, but one of the child-adult contacts does not occur, and the third most likely network has one teenager away from home, but all other contacts occurring. These estimates are also reasonable given our understanding of social behavior.

Fig 4.

Estimated probability distribution of contact networks, households with two 12–18 year olds and two 36+ year olds, with 95% confidence intervals. Members at home are shown in blue; those away from home are shown in white. Only networks with probability >0.02 are depicted.

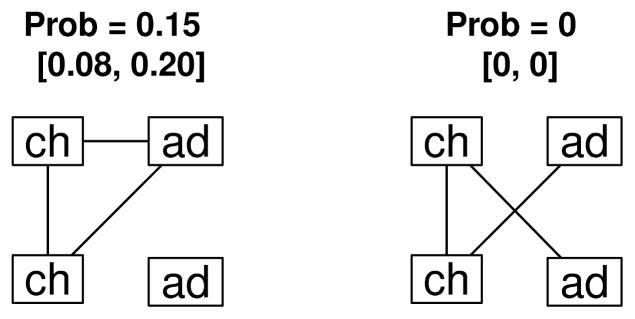
The dependency in our model can be seen by studying Figures 3 and 4. Networks which would be equally likely under an independence assumption have different estimated probabilities under our assumptions. For example, Figure 5 shows two possible contact networks and their probabilities computed under our model for a household with two 0–5 year olds and two 19–35 year olds. Under a random mixing assumption these two networks would have the same probability since they have the same numbers of child-child ties and adult-adult ties. An independence model which has age-specific contact probabilities but no latent variable effect would also assign the same probabilities to these two networks. Yet under our model, one of them has probability 0.15, and the other has probability 0. Thus, our assumptions give rise to a process very different from random mixing. The latent variable in our model creates dependencies which would not be captured in a model with only age-specific mixing probabilities.

Fig 5.

Illustration of dependency in our model. Under random mixing or under an independence model with age-specific contact probabilities but no latent variable, the two networks below would have the same probability.

4.2. Model Validity and Weak Identifiability

Our results suggest that our algorithm has succeeded at uncovering the parameter values and disentangled the home/away process from the contact process for our data set. However, it is possible that the identifiability is only weak. In this section we show results from a validity check evaluating our model and perform simulations to assess weak identifiability.

To check the validity of our model, we compare our estimates of “at home” probabilities to the percentage of respondents who report any contacts to household members. Since respondents are randomly sampled, these percentages are unbiased estimates of the probability of a person having at least one contact to another household member at home. The probability of being at home is greater than or equal to the probability of contacting at least one household member at home, since the latter event implies the former.

Table 5 compares MLEs of the probability of being at home to the estimated probability of being at home and contacting at least one household member. For 4 of 5 age groups, the estimated probability of being at home is greater than the estimated proportion of people contacting any household members at home, as we expect. The difference is statistically significant only for the oldest age group. For 6–11 year olds, the direction of the difference is opposite what we expect, but the statistically insignificant difference is small enough not to raise concern. Although the probability of being at home is necessarily greater than or equal to the probability of contacting anyone at home, we expect these probabilities to be close. Our validity check indicates that our model is producing reasonable results.

Table 5.

Validity check, all households

Age Category	Estimated probability of being at home	% of respondents with any at home contacts
0–5	0.90 [0.86, 0.95]	0.89 [0.83, 0.96]
6–11	0.92 [0.88, 0.98]	0.93 [0.87, 0.98]
12–18	0.89 [0.84, 0.94]	0.88 [0.81, 0.94]
19–35	0.90 [0.86, 0.94]	0.82 [0.75, 0.89]
36+	0.92 [0.89, 0.95]	0.80 [0.75, 0.85]

We performed a simulation study to assess whether data sets with the same size and distribution of household age compositions as ours contain enough information to estimate our parameters. The simulation procedure was as follows:

1. Choose values for the five “at home” probabilities and the 15 conditional contact probabilities.

2. Simulate 500 data sets with the same size and distribution of household age compositions as ours from the model using these parameters.

3. For each simulated data set, compute maximum likelihood estimates of the parameters.

4. Compute the mean of the MLEs over the 500 simulations and compare to the true value.

We performed simulations for two different sets of parameter values. First we set the conditional contact probabilities equal to our estimated contact probabilities, but we varied the “at home” probabilities in our simulation to test whether the method could detect the variation. (Recall that all of our estimated “at home” probabilities were near 0.90.) We chose the values 1.0, 0.9, 0.8, 0.7, and 0.6 for “at home” probabilities of the five age groups. Our results in Tables 6 and 7 indicate that the estimation procedure does a good job of uncovering the true “at home” probabilities, and a fair job of uncovering the conditional contact probabilities. The accuracy of the conditional contact probability estimates is highest when the two age groups have a high probability of being at home. These estimates are most accurate when one of the age groups is 0–5, whose probability of being at home is one, and least accurate when one of the age groups is 36+, who have the smallest probability (0.60) of being at home. Since our estimated “at home” probabilities from the actual data are all near 0.90, our conditional contact probability estimates are probably fairly accurate.

Table 6.

At home probabilities used for simulations, mean estimated at home probabilities over 500 simulations, and 2.5% and 97.5% quantiles of the estimates.

Age	Truth	Mean of estimates	95% Quantile Interval
0–5	1	1.00	[1.00, 1.00]
6–11	0.9	0.93	[0.87, 0.98]
12–18	0.8	0.85	[0.77, 0.92]
19–35	0.7	0.73	[0.68, 0.79]
36+	0.6	0.61	[0.57, 0.64]

Table 7.

Conditional contact probabilities used for simulations, mean estimated at home probabilities over 500 simulations, and 2.5% and 97.5% quantiles of the estimates.

Age 1	Age 2	Truth	Mean of estimates	95% Quantile Interval
0–5	0–5	1.00	1.00	[1.00, 1.00]
	6–11	0.90	0.89	[0.78, 1.00]
	12–18	0.67	0.67	[0.32, 0.99]
	19–35	0.99	0.96	[0.86, 1.00]
	36+	0.96	0.93	[0.81, 1.00]
6–11	6–11	1.00	0.94	[0.79, 1.00]
	12–18	1.00	0.93	[0.78, 1.00]
	19–35	0.96	0.89	[0.76, 1.00]
	36+	0.91	0.83	[0.72, 0.94]
12–18	12–18	0.88	0.80	[0.63, 0.98]
	19–35	0.65	0.59	[0.41, 0.78]
	36+	0.91	0.80	[0.71, 0.87]
19–35	19–35	0.80	0.75	[0.56, 0.99]
	36+	0.83	0.74	[0.64, 0.82]
36+	36+	0.89	1.00	[0.99, 1.00]

Our data set contains fairly high reported rates of contact. A data set with lower contact rates may not provide enough information to distinguish household members being away from home versus not being contacted. To investigate this, we performed a second simulation for which we reduced contact probabilities to obtain empirical data sets with households in which some respondents are home but don’t contact any other members. Our results, given in the supplementary material (Potter et al, 2011), show that in this type of data set the procedure does not work as well. The “at home” probabilities are underestimated, and the contact probabilities are overestimated.

5. Discussion

In this paper we infer the structure of within-household contact networks, which are a key component for models of epidemic spread. We show how to infer the probability distribution of the complete within-household contact network from individual-level data from one respondent per household in a random sample of households. By modeling the unobserved event that some members may be away from home on a given day, we incorporate dependency in contact behavior, resulting in a process different from random mixing. We also find the probability of all household members contacting each other on a given day to be substantially less than one. These two findings indicate that contact behavior reported in surveys is different from the contact patterns generally used for epidemic models and estimation methods. Our finding that contact probabilities are higher in households with 2–3 members than in households with 4+ members helps to explain the higher transmission rates found by Cauchemez et al (2009) in households with 2–3 members than in larger households.

The contact probability matrices show that contact between any two members is highly likely if both members are at home. All probabilities are over 50%, and most range from 90–100%. In any size household, 0–5 year olds are highly likely to contact other young children and adults, as we might expect. The contact probability is lowest between teenagers in any size household, as we might also expect. Our model succeeded at disentangling the contact process from the home/away process, and the estimated probabilities of being at home are all close to 90%.

The plots of the probability distribution of the contact network show that the complete network – in which all possible contacts occur – is the most likely. However, the probability of this network is lower than one might expect. We estimate this probability to be 0.49 in households with two 0–5 year olds and two 19–35 year olds, and 0.36 in households with two 12–18 year olds and two 36+ year olds. The dependency in contact behavior arising from our model is apparent in these plots.

We have made some strong assumptions for our model. First, we have assumed that the only dependence in ties arises from household members being away from home. Our data suggest that there is indeed an “away from home” effect on contact behavior, but other dependencies are likely to exist. For example, one parent contacting a child may reduce the probability that the other parent contacts the child, if one parent has more child care responsibilities. In addition, our assumption that the events of members being at home or away from home are independent is quite strong. Family members are likely to travel together, and in a household with small children, if one parent is away from home the other is probably more likely to be at home. Furthermore, we assumed that contacts occur independently conditional on members being at home. In fact, contact between two family members may influence their behavior with others, conditional on all of them being at home. We have also assumed that contact behavior does not change when a household member is away, other than the removal of contacts to that member. In fact, it is possible that contact density tends to increase when some members are away, violating this assumption. Our data do not contain information to estimate these other potential dependencies. We have estimated one dependency in contact behavior, informed by the data and by a reasonable social theory. Our model is a simplification of the true underlying process, and further data is required to estimate additional dependencies and assess whether our model captures the network structures relevant to the disease transmission process. We recommend collecting complete network data to analyze these patterns.

Finally, we’ve assumed that contacts depend on the age categories of the two members. This assumption is realistic, as evidenced by our different contact probability estimates in the matrices. However, contacts could also depend on gender. In particular, mothers may be more likely to contact children than fathers. Although our data set contains the gender of each respondent and of all contacts, it does not contain the gender of each household member. For this reason, including gender as a predictor is not straightforward.

Our predictions could be improved by collecting additional data. We recommend asking respondents whether they were at home on the day of the survey, whether contacted persons were household members, and whether each household member was at home on the survey day. It could also be useful to collect the gender of each household member. Based on our recommendation, the next implementation of POLYMOD in Belgium, as well as similar studies in Vietnam and Thailand, ask respondents to identify whether contacted people are household members (Horby 2011). In addition, we recommend collection of complete network data to validate our results and improve understanding of within-household contact behavior.

Our method can be used in other settings to infer networks from egocentric data. For example, our method could be used to infer household contact networks in cultures with larger household sizes than commonly found in Belgium. A study of household economic networks in a Malawian village found a mean household size of 9, rather than 3.24 as in our Belgian data set (Potter and Handcock, 2010). Our method could also be used to infer within-classroom networks or within-workplace networks from the POLYMOD data.

We have demonstrated that this method works reasonably well for small networks. As the network size increases, the proportion of the network reported by a single respondent decreases, but identifiability of the parameter vector depends on the number of age categories. As long as there is an adequate number of respondents in each age category, the parameter vector remains identifiable as network size increases. Computation time is an issue because the number of hidden configurations increases at a faster rate than network size. The number of hidden configurations depends on the number of age categories, the network size, the distribution of household age compositions, the number of respondents, and the number of reported contacts. Computation is still feasible for household networks with up to 10 members and for larger sizes if the number of age categories is reduced. Classroom, workplace, or daycare networks could be modeled with a single age category. With a single age category, estimation for networks with up to 50 members is feasible.

Our method requires a single respondent per network, a common sampling design for household studies. If multiple respondents per network are observed, their reports will not be independent, so the joint likelihood is not the product of the marginal likelihoods as we assumed. The independence assumption is reasonable for inference of small networks when respondents have been sampled at random from an entire country as in the POLYMOD study. For inference of much larger networks, with hundreds or thousands of members, it would be more convenient to sample multiple members per network and develop an inference technique accounting for the dependence in contact reports.

We have developed a model to infer complete within-household contact networks from egocentric data. Although our results are from a single survey, they are broadly relevant to epidemic models. Our model incorporates dependency in contact behavior by estimating a latent variable indicating which household members are at home, and our inferred contact structure departs from the standard random mixing assumption. In addition, we find higher contact probabilities in households with 2–3 members than in larger households. This should also be taken into account when estimating transmission parameters from household-level data. Finally, many epidemic models assume that all household members contact each other on a given day, but we find that the probability of all possible contacts occurring is actually fairly small. Estimation of contact probabilities and of disease transmission probabilities is often confounded, since disease outcomes are collected but detailed information about contact behavior is not. By shedding light on the contact structure, our work can help disentangle the contact process from the transmission process. Our findings can be used to improve epidemic models and estimation methods. As future work, we propose integrating our findings into these models and performing simulation studies to evaluate their impact on results.

APPENDIX A: PROOF OF IDENTIFIABILITY

Theorem A.1. Identifiability

The latent variable model described in 3.1 is identifiable.

Proof

To see that our model is identifiable, suppose for the sake of contradiction that two different sets of probability parameters produce the same probability distribution. Assuming that the two probability distributions are equal, we will show that the parameterizations must be identical, which is a contradiction.

We will denote the two different probability parameter vectors p_A and p_B, so the elements of p_A which are the at home indicators are denoted p_j,A for j ∈ {1, …, 5}, and the contact probabilities are denoted p_rs,A for r, s ∈ {1, …, 5}. The elements of p_B have analogous notation. Recall that the observations used to estimate our model parameters represent households of diverse sizes and age compositions. With an infinite amount of data, any type of household may be represented in the data set. Therefore, a household containing only two members, both in age category k, may be in the data set. Our observed outcome is the presence or absence of contact to the other member. Keeping our notation from the description of the likelihood, the observed outcome is denoted w_k and is equal to either zero or 1. (The other elements of w are zero since there are no household members in the other age categories.) Using our formula for the likelihood and the assumption that probability distributions are equal under parameterizations A and B, we have:

$$\text{P}(w_k=1\mid {\mathbf{p}}_{\mathbf{A}})=p_{k,A}^2{p}_{kk,A}=\text{P}(w_k=1\mid {\mathbf{p}}_{\mathbf{B}})=p_{k,B}^2{p}_{kk,B}.$$ (A.1)

We want to show that the corresponding elements of p_A and p_B are equal. For this, we’ll need information from a different household, one which contains three members in age category k. For this household, the sufficient statistic is again w_k, which can now take on the values 0, 1, or 2. Under our assumptions,

$$\text{P}(w_k=2\mid {\mathbf{p}}_{\mathbf{A}})=p_{k,A}^3{p}_{kk,A}^2=\text{P}(w_k=2\mid {\mathbf{p}}_{\mathbf{B}})=p_{k,B}^3{p}_{kk,B}^2.$$ (A.2)

Dividing (A.2) by (A.1), we obtain:

$$p_{k,A}{p}_{kk,A}=p_{k,B}{p}_{kk,B}.$$ (A.3)

Now dividing (A.1) by (A.3) yields:

$$p_{k,A}=p_{k,B}.$$ (A.4)

Thus we have shown that the “at home” probability parameters are the same under parameterizations p_A and p_B. To see that the conditional contact probabilities are also equal, consider a household containing two members in age categories r and s, and suppose the respondent is in age category r. Our sufficient statistic is denoted w_s, which can take on values 0 or 1. We have:

$$\text{P}(w_s=1\mid {\mathbf{p}}_{\mathbf{A}})=p_{s,A}{p}_{r,A}{p}_{rs,A}=\text{P}(w_s=1\mid {\mathbf{p}}_{\mathbf{B}})=p_{s,B}{p}_{r,B}{p}_{rs,B}.$$ (A.5)

Since we have already proven that p_s,A = p_s,B for all age categories s, it follows that p_rs,A = p_rs,B. Thus the parameter vectors p_A and p_B are identical. Since we have contradicted our assumption that they were distinct, we’ve proven that our model is identifiable.