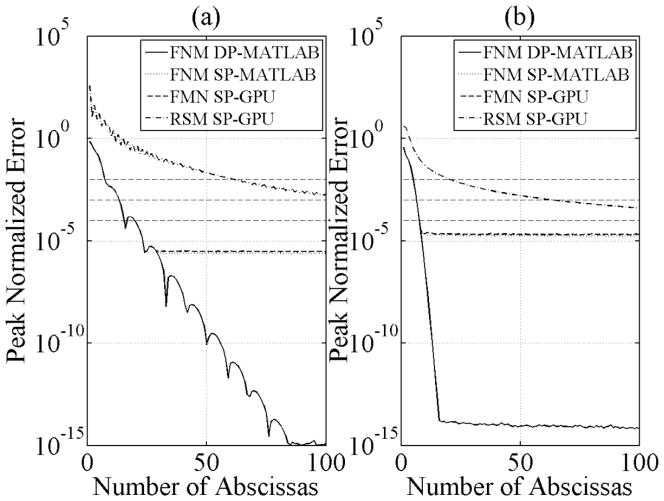
Fig. 6.
Peak normalized relative errors in the azimuth-depth plane for a single rectangular piston using parameters identical to those used to generate Fig. 5, as a function of number of abscissas for (a) the near-field out to 1 far-field transition distance from the piston and (b) for the far-field between 1 and 10 far-field transition distances from the piston. The reference field was calculated in MATLAB in double-precision using 200 abscissas. Results for FNM in double-precision MATLAB (solid), FNM in single-precision MATLAB (dotted), FNM in single-precision GPU (dashed), and RSM in single-precision GPU (dash-dot) are shown. The dashed horizontal lines indicate 1, 0.1, and 0.01% relative error. Note that the single-precision FNM curves track the double-precision FNM curve up the respective numerical accuracy limits of each method. In the near-field, the FNM in single-precision GPU converges to within 1, 0.1, and 0.01% error with 8, 14, and 16 abscissas, respectively, and correspondingly 612, 1262, and 3962 abscissas for the RSM.