Assumption weighting for incorporating heterogeneity into meta-analysis of genomic data

Abstract

Motivation: There is now a large literature on statistical methods for the meta-analysis of genomic data from multiple studies. However, a crucial assumption for performing many of these analyses is that the data exhibit small between-study variation or that this heterogeneity can be sufficiently modelled probabilistically.

Results: In this article, we propose ‘assumption weighting’, which exploits a weighted hypothesis testing framework proposed by Genovese et al. to incorporate tests of between-study variation into the meta-analysis context. This methodology is fast and computationally simple to implement. Several weighting schemes are considered and compared using simulation studies. In addition, we illustrate application of the proposed methodology using data from several high-profile stem cell gene expression datasets.

Availability: http://works.bepress.com/debashis_ghosh/50/

Contact: ghoshd@psu.edu

1 INTRODUCTION

In recent years, with the extensive usage of microarray and other high-throughput technologies in biomedical research, there has been a rapid growth in the amount of publicly available datasets. The NCBI Gene Expression Omnibus (GEO, http://www.ncbi.nlm.nih.gov/geo/), the EBI ArrayExpress (http://www.ebi.ac.uk/arrayexpress/) and the Stanford Microarray Database (SMD, http://smd.stanford.edu/) are a few examples of widely used public internet repositories. These resources allow researchers to further exploit the information in these data, especially in the form of meta-analysis. How to effectively integrate information of microarray datasets from multiple studies is becoming an increasingly important problem. The other area of genomics that has increasingly relied on the use of meta-analysis has been genome-wide association studies (GWAS); some seminal studies in this field are Scott et al. (2007) and Willer et al. (2008).

Returning to the microarray example, the most common type of analysis is the detection of differentially expressed genes, especially for the case of two groups of samples, namely treatment and control. Combining information from multiple datasets is expected to increase the power for differential expression analysis. Many methods for meta-analysis addressing this type of problem have been proposed and reviewed in recent years. An incomplete list includes the P-value combining approach of Rhodes et al. (2002), the GeneMeta method by Choi et al. (2003), RankProd method by Hong et al. (2006), the metaArray approach of Choi et al. (2007), a hierarchical model put forth by Scharpf et al. (2009) and the mDEDS algorithm of Campain and Yang (2010). In this latter paper, a comparison between several meta-analysis approaches was considered as well.

One important issue that has received limited discussion in most of this literature is the assessment of the concordance of data among different studies and the integration of this information into further analysis. This problem is very well understood in the classical meta-analysis problem and tests for between-study heterogeneity have been accordingly developed; see Normand (1999) for a discussion. However, it becomes conceptually problematic to extend this approach directly to the genomic meta-analysis problem, as one has to perform G tests of heterogeneity and then determine based on the result of the tests whether or not meta-analysis is feasible for every single gene. It will be the case that there will be some genes that will show significant evidence for between-study heterogeneity. Thus, the meta-analysis will be done on a subset of genes, contrary to the approaches described in the previous paragraph. In addition, there are issues of ‘pre-testing’ and model selection that arise which complicate the analysis and interpretation of such a meta-analysis.

The evidence for between-study heterogeneity in these high-throughput genomic data settings is growing. One potential cause is errors in mapping the proper gene to the microarray annotation (Dai et al., 2005). This can be viewed as a technical mistake that leads to between-study variation. A more biologically oriented cause is that samples being profiled actually represent subtypes of different disease groups. This has been mostly famously explored in breast cancer (Sorlie et al., 2001), prostate cancer (Tomlins et al., 2005) and leukaemia (Vardiman et al., 2002). Thus, the presence of subtypes of samples leads to the between-study heterogeneity. A final reason is the fact that due to the diversity of labs generating these data, there will inherently exist between-lab variation and more generally, batch effects. A recent review by Leek et al. (2010) demonstrates the existence of batch effects in a variety of high-throughput genomic datasets.

Two questions then naturally arise from these findings. First, how does one assess between-study variation using high-throughput genomic data? Second, how can one incorporate the between-study variation into the analysis. Measures of reproducibility have been proposed by Parmigiani et al. (2004), Lee et al. (2004) and Li et al. (2011). Implicitly, once these measures are calculated, one would then calculate a summary measure on genes that were ‘sufficiently’ reproducible. Another approach would be to model the between-study variation; this has been done by Shabalin et al. (2008) and Scharpf et al. (2009).

Lai et al. (2007) developed a framework for integrating two studies for differential expression analysis that entails assessment of global concordance. In contrast, the approach developed in this article will utilize measures of gene-wise or local concordance. Other methods have been proposed to assess the global concordance of studies, such as the concordance correlation coefficient (CCC) by Miron et al. (2006). Lu et al. (2010) proposed a multi-class correlation measure to seek for genes of concordant inter-class patterns across studies. The between-study variation can also be modelled as variance components or other parameters in the joint modelling frameworks of GeneMeta (Choi et al., 2003) and Scharpf et al. (2009). These algorithms will tend to be more computationally intensive than what is proposed in this article.

In this article, we focus on meta-analysis of microarray datasets for differential expression analysis. We take the viewpoint that the major goal in these studies is selection and prioritization of genes for further validation studies. We exploit the weighted hypothesis testing framework proposed by Genovese et al. (2006) and propose an ‘assumption weighting’ methodology. To be specific, we will use weights that assess between-study heterogeneity and incorporate them into a multiple testing procedure. We also note in passing that the use of weights for characterizing the assumptions needed for meta-analysis is a novel application of this weighted hypothesis testing framework. We proposed four different weighting schemes, including two based on an assessment of the concordance of the test statistics of different studies—the I² index (Higgins and Thompson, 2002)—and two based on a newly proposed measure of expression correlation between studies. The performance of these methods are assessed through simulation studies as well as applications to a set of stem cell studies.

2 METHODS

2.1 Weighted hypothesis testing framework

Before describing the proposed methodology, we briefly review the weighted hypothesis testing framework of Genovese et al. (2006) for multiple hypothesis testing. It is summarized in Box 1. The method incorporates prior information about the hypotheses in the form of P-value weights for each hypothesis, while maintaining control of the false discovery rate (FDR) for multiple hypothesis testing. The procedure is as follows: first assign weights W_i>0 to the i-th null hypothesis (1≤i≤n) such that 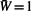; then compute q_i=p_i/W_i for each i, where p_i is the unweighted P-value for testing the i-th hypothesis; and last, if it is desired to control the FDR at a specific α, apply the Benjamini and Hochberg (1995) procedure at level α to the q_i's. In practice, if we simply wish to pick out the top most significant genes, we can directly use the ordering of the q_i's and omit the B-H procedure in the last step. Genovese et al. showed that if the assignment of weights is positively associated with the null hypothesis being false, then the procedure improves power, and that even if the assignment of weights is poor, power is only reduced slightly.

Box 1. Weighted B-H procedure of Genovese et al. (2006).

1. Let p₁,…, p_n denote the n P−values with associated weights W₁,…, W_n.

2. Define q_i=p_i/W_i.

3. Let q₍₁₎≤q₍₂₎≤···≤q_(n) denote the ordered values.

4. Find

   

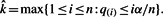
5. If 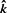exists, then reject null hypotheses corresponding to 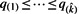. If the set in (d) is empty, reject nothing.

2.2 Proposed methodology

We consider S studies to be combined. Within each study, there are two groups of samples (control and treatment), and the goal is to find genes that are differentially expressed between the two groups. Let p_gs be the P-value for the two sample t-test between treatment and control for gene g (1≤g≤G), study s (1≤s≤S). Here, as well as in following steps, we used the basic two sample t-test to obtain the t-statistic and P-values. However, this can be straight-forwardly generalized to other variations of the t-test. Some tests developed in recent years might be more preferable in the analysis of gene expression data, such as the moderated t-statistic by Smyth (2004).

By Fisher's combined probability test, we can combine the P-values from the S studies to obtain a single test statistic for each gene: X²_g=−2∑_s log(p_gs). Under the null hypothesis that the gene is not differentially expressed in any of the studies, and that the studies are independent, X²_g has a chi-squared distribution with 2S degrees of freedom. Thus for each gene we can obtain a Fisher's P-value, p_g=P(χ²_2S>X²_g), for testing differential expression between the two groups combining all the studies. However, Fisher's combined test does not specifically account for heterogeneity among the studies.Thus, a significant Fisher's P-value does not necessarily reflect a consensus result. A small Fisher's P-value could be driven by a single study with an extremely small P-value; or even if many of the studies had small P-values, it could be the case that differential expression are of different directions among the studies, thus making it hard to interpret the combined test.

To account for this problem, we will adjust the Fisher's P-value by using the methodology summarized in Box 1.

In our case, the prior information is the degree of heterogeneity among the studies. Let U be a measure of heterogeneity among the studies, such that large values of U represent less heterogeneity. Denote by U_g the heterogeneity measure for gene g. Define weights 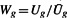, where 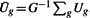, so that the weights have mean 1. Then the P-value weighting method gives us the adjusted P-value for each gene q_g=p_g/W_g. By this construction, genes with homogeneous expression patterns among the studies are assigned larger weights, resulting in smaller adjusted P-values, which are more likely to be found significant. In contrast, genes displaying heterogeneity are down-weighted, resulting in larger adjusted P-values and are less likely to be found significant. We shall explore and compare several different measures of heterogeneity to incorporate the weighted multiple testing procedures.

2.3 Using I² as weight

2.3.1 I²: definition and weighting scheme

One approach is to assess the concordance of the test statistics of the different studies. A common measure of this kind used in meta-analysis is the Q-statistic (Cochran, 1954). To adjust for the dependency of the Q-statistic on the number of studies, an I² index (Higgins and Thompson, 2002) was proposed based on the Q-statistic. We shall adopt the I² index as one method of weighting.

Let T_gs be the t-statistic for the two sample t-test between control and treatment, for gene g(1≤g≤G), study s(1≤s≤S). The Q-statistic for gene g is defined as 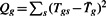, where 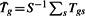. The I² index compares the Q-statistic with its expected value assuming homogeneity (which is S−1). The I² index for gene g is

if Q_g>S−1 and defined to be 0 if Q_g≤S−1. Therefore, a large I²_g corresponds to higher heterogeneity for that gene, in which case we wish to down-weight.

We define U_1g=(I²_g+10⁻⁵)⁻¹ and the corresponding weights W_1g≡U_1g/Ū_1g so that higher heterogeneity corresponds to lower weights. Adding 10⁻⁵ in the denominator is just for technical purposes so that the weights are well defined when I²=0.

2.3.2 Accounting for direction of change

The I² index measures the heterogeneity of the test statistics for different studies, but it does not explicitly take into account the direction of the change, i.e. in our case the sign of the t-statistic. Define C_g=min{∑_sI_{Tgs>0}, ∑_sI_{Tgs<0}}/S for gene g. Thus 0≤C_g≤0.5. Small values of C_g indicate that most studies display a change of the same direction between treatment and control, while large values of C_g indicate a relatively stronger disagreement on the direction of change among the studies for that particular gene. Define U_2g=W_1g/(C_g+0.01) and the corresponding weights W_2g≡U_2g/Ū_2g. Genes that show discordant directions of change would be further down-weighted in adjusting the P-values. Adding 0.01 in the formula of U_2g is to avoid the denominator being 0.

2.4 Using correlation as weight

2.4.1 Correlation measurement between a pair of studies

Another intuitive way of quantifying heterogeneity is to assess the expression correlation of a gene between studies. We start with assessing the correlation of expression values between two studies for a given gene. For simplicity of notation, we drop the subscripts g and s, and let x_ki(1≤i≤n_k) and y_ki(1≤i≤m_k) be the expression value of gene g for class k (k=0, 1), sample i of the first study and the second study, respectively. For the case n_k=m_k (k=0, 1), a naive way of assessing the expression correlation between the two studies is to directly take the sample correlation of (x₀₁,…, x_0n0, x₁₁,…, x_1n1) and (y₀₁,…, y_0m0, y₁₁,…, y_1m1). However, this approach is not adaptable to cases where n_k≠m_k, and it also ignores the exchangeability of samples within a group.

We shall introduce a new way of computing the correlation addressing these two issues. In order for the new method to still fit into the general framework of sample correlation, we need to construct paired samples from the two studies. The construction of paired samples are based on the following two considerations: (i) since we are interested in the comparison between treatment and control, treatment samples from the two studies should be paired together, and control samples from the two studies should be paired together, while it does not make sense to pair a treatment sample from one study with a control sample from another study. That is to say sample pairs should be created between (x_k1,…, x_knk) and (y_k1,…, y_kmk) for the same k. (ii) The ordering of samples within a group should not matter. That is to say, if we have a permutation of the samples (x_k1,…, x_knk), the results should remain the same. Based on these two considerations, we create paired samples by taking all possible pairs between (x₀₁,…, x_0n0) and (y₀₁,…, y_0m0), and all possible pairs between (x₁₁,…, x_1n1) and (y₁₁,…, y_1m1). Thus, the resulting sample vectors of the two studies are in the form of:

where x_ki=(x_ki,…, x_ki) is a vector of length m_k, and y_k=(y_k1,…, y_kmk). Both resulting sample vectors are of length n₀m₀+n₁m₁. We shall use the sample correlation of these two sample vectors, denoted by ρ, as our measurement of the expression correlation between the two studies. Intuitively, differential expression of the same direction in both studies will lead to a positive ρ. Similarly, differential expression in opposite directions in the two studies will lead to a significantly negative ρ; no differential expression in one or both studies will lead to an insignificant ρ.

Thus, we may calculate a correlation measurement ρ_gss′ for each gene g and each pair of studies s and s′ [there are S(S−1)/2 pairs of studies in total]. We use these ρ's to construct another measurement of heterogeneity U_3g for each gene. Let U_3g be the absolute value of the mean ρ_gss′ for all pairs of studies raised to the power of 10, that is

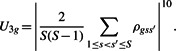Defining U_3g in this way, we will expect large values of U_3g if most of the studies display differential expression in the same direction; we will expect small values of U_3g if differential expression only occur in a small fraction of the studies, in which case most of the ρ_gss′ are small, or if the studies are not consistent in the direction of differential expression, in which case the positive ρ's and negative ρ's will be washed out when we take the mean. Thus, large values of U_3g correspond to homogeneous patterns of differential expression among the studies. Raising the mean correlation to the power of 10 is used to amplify the effects of weighting, as we found that using versions of U_3g without raising the power did not lead to change in the weights relative to an unweighted scheme (data not shown). As before, let W_3g=U_3g/Ū_3g be the weights, and obtain the adjusted P-values by dividing the original Fisher's P-values by the weights.

2.4.2 Correlation measurement among S studies

Previously, we assessed the correlation of expression levels among S studies by breaking down the studies into pairs. However, we may adopt the idea we used for deriving correlation for a pair of studies to directly construct a measurement of correlation among all the studies.

Similar to before, we shall construct paired samples. Again, it only makes sense to pair up samples coming from the same class (i.e. both samples belong to control group or both samples belong to treatment group), but now the two samples may come from any two studies among all the studies. Thus, we pool all the control samples from the S studies and take all possible pairs of samples from this pool, and do the same thing for the treatment samples.

Suppose for study s there are n_s0 replicates for the control group and n_s1 replicates for the treatment group. Then there are a total of N₀=∑_sn_s0 control samples and N₁=∑_sn_s1 treatment samples from all the studies. Denote by x_0i (1≤i≤N₀) the expression values for the control samples from all the studies, and x_1i (1≤i≤N₁) the expression values for the treatment samples from all the studies. Create two sample vectors as follows:

where x_ki=(x_ki,…, x_ki) is a vector of length N_k−1, and x^*_ki=(x_k1,…, x_k(i−1), x_k(i+1),…, x_kNk) is a vector of all the samples from group k excluding x_ki. Both resulting sample vectors are of length N₀(N₀−1)+N₁(N₁−1). Let λ be the sample correlation between these two sample vectors. We shall use λ as a measurement of expression correlation among all studies. It can be seen from the construction of λ that consistent differential expression will lead to large values of λ, whereas inconsistent differential expression or non-differential expression will lead to small values of λ.

Denote by λ_g the λ value computed for each gene. Let U_4g=|λ_g|¹⁰ be a fourth measure of heterogeneity among studies, with large values of U_4g corresponding to less heterogeneity, and construct corresponding weights W_4g=U_4g/Ū_4g. The correlation is raised to the power of 10 to be consistent with the mean correlation case.

3 RESULTS

3.1 Simulation studies

We conducted simulation studies to assess the performance of our weighted P-value methods in detecting differential expression across multiple studies. We compared results from the four different weighting schemes, as well as from existing meta-analysis methods RankProd (Hong et al., 2006) and GeneMeta (Choi et al., 2003).

The simulation study focuses on assessing the methods' abilities of efficiently selecting and prioritizing genes that demonstrate consistent differential expression patterns across the studies. The key issue here is ‘consistency’ across studies, and it consists of two aspects: (i) the proportion of studies that display significant differential expression out of all the studies; (ii) whether gene expression change occurs in the same direction for the studies that do show differential expression. We conducted two sets of simulation studies, simulation-I and II, focusing on these two aspects, respectively.

The detailed simulation setup is described as follows. For both sets of simulations, we simulated a scenario of 10 studies to be combined and a total of 10 000 genes. Each study consists of a treatment group and a control group. The sample sizes were randomly generated for each study and each group, ranging from 4 to 15. For simulation-I, we simulated five categories (scenarios) of differential expression: differential expression in all 10 studies, in 8 studies, 6 studies, 4 studies and 2 studies. In all, 500 genes were assigned to each of these categories, and the rest of the genes were assigned to be not differentially expressed in any of the studies. For simulation-II, we simulated two groups of categories (scenarios) of differential expression. For the first group, differential expression occurs in all 10 studies, but we split this group further into three categories: all 10 studies show differential expression of the same direction; 7 out of 10 studies show differential expression in one direction, while the rest 3 show differential expression in the other direction; 5 out of 10 studies show differential expression in one direction, while the rest 5 in the other direction. For the second group, differential expression occurs in 6 out of 10 studies, and we also split this group into three categories: all 6 studies show differential expression of the same direction; 4 out of 6 studies show differential expression in one direction, while the rest 2 show differential expression in the other direction; 3 out of 6 studies show differential expression in one direction, while the rest 3 in the other direction. In all, 500 genes were assigned to each of the six categories described above, and the rest of the genes were assigned to be not differentially expressed in any of the studies. The simulation setups described above are summarized in Table 1.

Table 1.

Summary of the category setups for simulation-I and II

Simulation-I	Categories	1	2	3	4	5	6
Number of differentially expressed studies out of 10		10	8	6	4	2	0
Direction of differential expression across differentially expressed studies		Same direction	Same direction	Same direction	Same direction	Same direction	Same direction
Simulation-II	Categories	1	2	3	4	5	6
Number of differential expression studies out of 10		10	10	10	6	6	6
Direction of differential expression across differentially expressed studies		Same direction	7 ↑ 3 ↓	5 ↑ 5 ↓	Same direction	4 ↑ 2 ↓	3 ↑ 3 ↓

‘↑’ and ‘↓’ are only used to indicate different directions of change, and are interchangeable.

We use a random effects linear model to model the gene expression measurements. The expression intensity of the i-th sample from group k (k=0, 1) of study s for gene g was simulated from x_gsik~N(μ_gsk, σ²_err). The mean expression level of gene g for the control group of study s is modelled as μ_gs0=μ+α_g+β_s+(αβ)_gs, where μ represents the overall mean expression level, α_g~N(0, σ²_gene) represents the gene effect, β_s~N(0, σ²_study) represents the study effect and (αβ)_gs~N(0, σ²_int) represents the gene–study interaction. For non-differentially expressed genes, the mean expression level for the treatment group is the same as the control group, i.e. μ_gs1=μ_gs0. For differentially expressed genes, we model the difference of mean expression between treatment and control group as μ_gs1−μ_gs0=δ+ν_g+ϵ_gs, where δ represents the overall mean difference, ν_g~N(0, σ²_diff) represents the gene effect of the difference and ϵ_gs~N(0, σ²_derr) represents the gene–study interaction of the difference.

We conducted the simulation using two different sets of parameter choices. In order to get an idea of the general magnitude of parameters in real data, we fitted the above model on a set of microarray gene expression data from a series of stem cell studies (Chin et al., 2009, Guenther et al., 2010, Newman and Cooper, 2010 and Chin et al., 2010). The first set of parameter choices is based on estimates from the stem cell study data, with μ=5, σ²_gene=2.5, σ²_study=0.7, σ²_int=0.5, σ²_err=0.3, δ=0.8, σ²_diff=0.15, and σ²_derr=0.3. We also used a second set of parameter choices with a larger gene effect but smaller effects for the other terms, with μ=5, σ²_gene=6.25, σ²_study=0.49, σ²_int=0.25, σ²_err=0.16, δ=0.8, σ²_diff=0.0016 and σ²_derr=0.0256.

Seven methods are tested out for simulation-I and II, respectively: Fisher's method, our weighted methods with four different weighting schemes, RankProd (Hong et al., 2006) and GeneMeta (Choi et al., 2003). For Fisher's method and our weighted methods, we applied the Benjamini–Hochberg (1995) procedure to the P-values/weighted P-values to control for the FDR. For RankProd (Hong et al., 2006) and GeneMeta (Choi et al., 2003), we used the inherent options provided in their R functions to control for the FDR. For all the methods, the resulting lists of significant genes are obtained controlling for FDR to be <0.05.

To assess the performance of the methods, we calculated the proportion of rejections (i.e. proportion of genes found to be significant under FDR<0.05) for each category in simulation-I and II. That is, for each category, we count the number of rejections (significant genes) in that category and divide it by the total number of genes in that category. Both simulations were repeated 50 times, and the final results were averaged over the replicates. Since our goal is to select genes that display consistent differential expression behaviour across studies, we would expect to see a higher proportion of rejections for those categories whose genes were simulated to be differentially expressed in a larger number of studies; vice versa, we would expect a lower proportion of rejections for those categories whose genes are only differentially expressed in very few studies; also, we would expect a lower proportion of rejections for those categories whose genes were differentially expressed in different directions across studies.

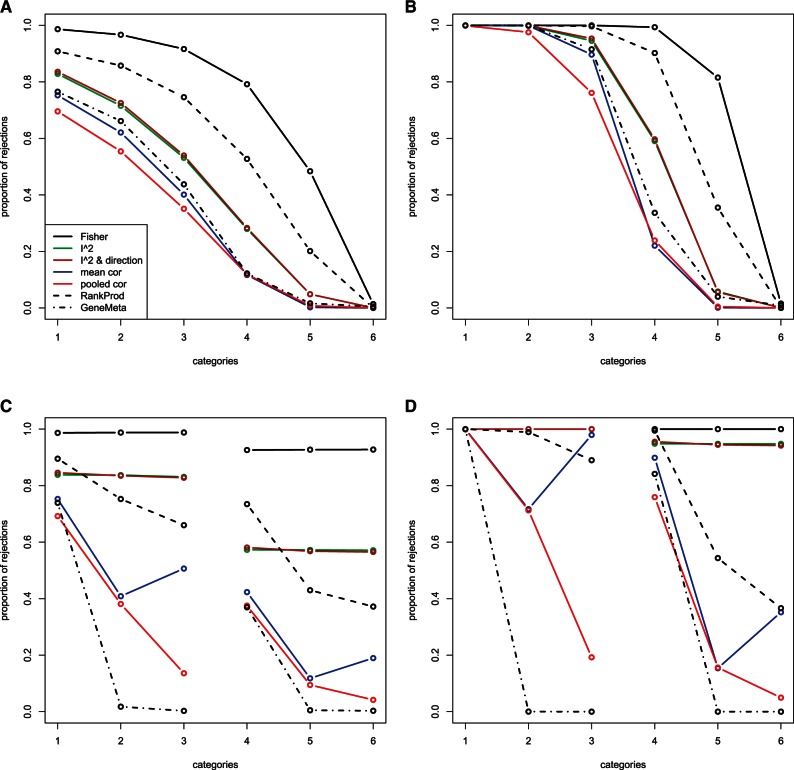
To better visualize the results, we plotted the proportion of rejections against categories, for both simulation-I and II, and both parameter settings (Fig. 1). For simulation-I, the number of studies in which the genes differentially express decreases from 10 to 0 throughout Categories 1–6 (Table 1). Thus, we would expect the proportion of rejections to decrease throughout Categories 1–6. The faster the proportion of rejections drop, the more sensitive the method is to inconsistent expression patterns across studies. As we can see from plots (A) and (B) in Figure 1, for both parameter settings, our weighted hypothesis testing methods, especially the two weighting schemes based on correlation, show a relatively higher sensitivity to inconsistent expression patterns across studies. Out of the seven methods, Fisher's method appears to be the least sensitive to inconsistent expression patterns, rejecting a large proportion of genes even when they are only differentially expressed in 2 out of 10 studies (Category 5). RankProd (Hong et al., 2006) comes next in comparison. The proportion of rejections for RankProd is significantly less than Fisher's method for genes that only differentially expressed in a small number of studies. Next in comparison is our weighted methods with weights based on the I² statistic. The methods that appear to be most sensitive to inconsistent expression patterns across studies are GeneMeta (Choi et al., 2003) and our weighted methods with weights based on correlation. The weighted method based on pooled correlation seems to be the most sensitive, with proportion of rejections starting to drop for genes that differentially express in 6 out of 10 studies (Category 3), and significantly dropping for genes that differentially express in 4 out of 10 studies (Category 4). The above observations are more obvious in the case of the second parameter setting, where all seven methods start off rejecting almost all the genes that differentially express in all 10 studies, and end up rejecting almost none of the genes that differentially express in none of the studies, but the proportion of rejections drop at different rates for the seven methods throughout the categories, with the pooled correlation weighted method most sensitive to inconsistent expression patterns. For the first parameter setting, it seems that methods that are more sensitive to inconsistent expression patterns tend to have relatively less power in detecting genes that do differentially express in all the studies. In this case, the scientist would need to consider the trade-off.

Fig. 1.

Plots showing the proportion of rejections for each category for simulation-I and II, for two parameter settings, respectively. (A) Simulation-I: Paramater-I; (B) Simulation-I: Paramater-II; (C) Simulation-II: Paramater-I; (D) Simulation-II: Paramater-II.

Note that Category 6 in simulation-I can been seen as an examination of the ‘specificity’ of the methods. Ideally, under any criterion, genes that do not differentially express in any of the studies should not be rejected. We can see from the plots that the proportion of rejections for Category 6 is very close to 0 for all the methods under both parameter settings. As the plot only shows the average result across the 50 simulation runs, we also checked the actual rejection proportions for each run to make sure that they were consistently low across simulations. In fact, our two weighted methods based on correlation performed the best in this aspect, not rejecting a single gene in Category 6 in all 50 simulation runs for both parameter settings.

For simulation-II, we would expect a lower proportion of rejections for Categories 2 and 3 compared to 1, and Categories 5 and 6 compared to 4, since genes in Categories 2, 3, 5 and 6 differentially express in different directions across the studies, especially for Categories 3 and 6, which are the extreme cases where differential expression occurs in one direction for half the studies and the other direction for the other half of the studies (Table 1). Results for simulation-II are shown in plots (C) and (D) in Figure 1. Fisher's method and the two weighted methods based on I² do not appear to be sensitive to different directions of DE across studies. For these three methods, the proportion of rejections are almost the same for genes that differentially express in the same number of studies, regardless of whether the direction of change is the same across the studies. For RankProd (Hong et al., 2006), GeneMeta (Choi et al., 2003) and the two weighted methods based on correlation, the proportion of rejections drop for genes that differentially express in different directions across studies. GeneMeta seems to be the most sensitive, with proportion of rejections close to 0 for all the categories with inconsistent DE direction. Our pooled correlation weighted method comes up next in comparison, with proportion of rejections dropping significantly for categories with inconsistent DE direction, especially for Categories 3 and 6, where the inconsistency of DE direction is the most extreme.

Summarizing the results from simulation-I and II, our weighted method with pooled correlation weighting scheme and GeneMeta (Choi et al., 2003) seem to be the two more competitive methods out of the seven methods tested, with regard to our goal of selecting genes that display consistent differential expression patterns, where ‘consistency’ is evaluated from two aspects mentioned previously addressed by the two simulations, respectively. Notice that under our simulations, it is expected that GeneMeta performs well, since the model we used to simulate the data is essentially the same model that GeneMeta uses to analyse the data. As discussed above, our weighted method with pooled correlation weighting scheme shows competitive results compared with GeneMeta, but our method does not rely on assumptions such as normality of the data, or more importantly, the structure of the model.

To get some sense of how the methods perform with non-normal data, we also simulated the expression data with ϵ_gs generated from the log of a gamma distribution. The resulting plots look very similar to those in Figure 1. Power is generally lower for all the methods and categories, but the trends of the plots and the relative comparisons between the methods remain almost the same.

During implementation of our weighted methods, we also find that they are significantly more efficient in terms of computing time, compared to RankProd (Hong et al., 2006) and GeneMeta (Choi et al., 2003), both of which involve permutations in the analysis process. In an experiment of the time costs of the methods, we implemented the three methods on a set of real data (described in the next section of the article), and the results are summarized in Table 2, where the time for our weighted method indicates the time used to achieve results for all four weighting schemes.

Table 2.

Summary of the time costs of the three methods (in seconds)

Method	User time	System time	Elapsed time
Weighted methods	175.701	0.430	176.449
RankProd	1174.512	26.272	1203.214
GeneMeta	274.749	13.801	289.317

3.2 Application to stem cell data

We applied the weighted P-value methods to a set of microarray data studies from four stem cell papers (Chin et al., 2009, Guenther et al., 2010, Newman and Cooper, 2010 and Chin et al., 2010). We focus on differential expression analysis between human-induced pluripotent stem (hiPS) cells and human embryonic stem (hES) cells. Some of the studies contain other samples such as human fibroblasts, but we only used samples from hiPS cells and hES cells. Studies that did not have at least two samples for each group (hiPS and hES) were excluded due to the inability to perform the t-test, leaving us nine studies in total. All the studies used the Affymetrix Human Genome U133 Plus 2.0 Array platform, which contains 54 675 features (probesets). For all the studies, we directly used the data pre-processed by the original contributors and did not perform any additional normalization, except for taking the log for data that were not already on the log2 scale.

We performed a two sample t-test between the hiPS cell samples and the hES cell samples for the nine studies and applied the Fisher's combined probability test as well as the weighted P-value methods using the four different weighting schemes. To adjust for multiple hypothesis testing, we applied the Benjamini–Hochberg (1995) procedure to the unweighted Fisher's P-values as well as the four kinds of weighted P-values, controlling the FDR at the 0.05 level. In all, 16 508 out of 54 675 features showed up to be significant by the unweighted Fisher's method. This seems to be an abnormally high proportion of significant features, and may be due to the fact that Fisher's test is prone to be driven by significant results of single studies. On the other hand, for the weighted methods, the weighting scheme based on I² index yields 777 significant features; the weighting scheme based on I² index and accounting for direction yields 670 significant features; the one based on mean correlation has 778 features showing up significant and the one based on pooled correlation has 196 features showing up significant.

We also performed the RankProd method by Hong et al. (2006) and the GeneMeta method by Choi et al. (2003) on this set of data. Based on controlling the FDR at the 0.05 level, the RankProd method found 2893 significant up-regulated (iPS compared with hES) features and 1996 significant down-regulated features, while the GeneMeta method found 2021 significant features for a two-sided test. Notice that the different methods resulted in significant gene lists of different sizes. Fisher's method resulted in an abnormally large number of significant features. Our weighted methods result in relatively smaller lists of significant features compared with RankProd (Hong et al., 2006) and GeneMeta (Choi et al., 2003). The weighted method based on pooled correlation seems to be the most conservative. This observation agrees with the simulation results.

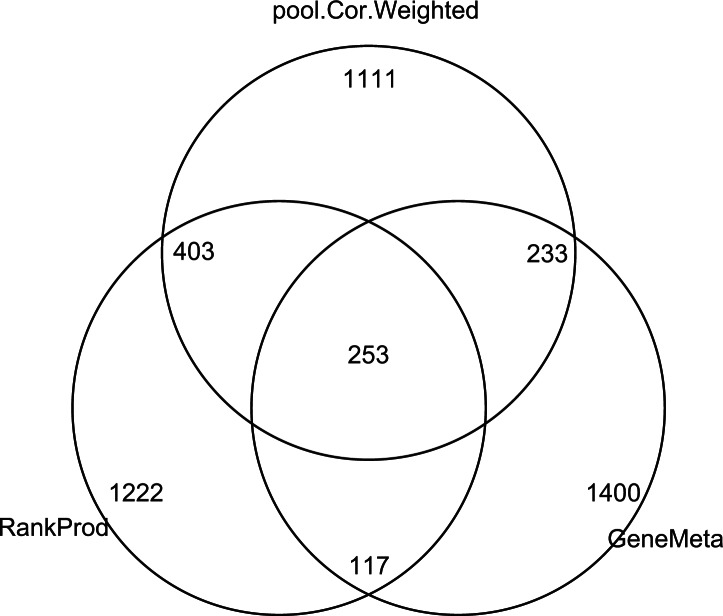
In order for the selected features lists from different methods be more comparable in size, we created lists of the top 2000 features for all the methods, disregarding the FDR, by selecting the features with the smallest P-values/weighted P-values/q-values for each of the methods. Figure 2 is a venn diagram displaying the overlap of the top 2000 features found respectively by using our pooled correlation weighted method, the RankProd method and the GeneMeta method. The fact that a significant number of features were only selected by one of the methods shows that these methods rank features from different perspectives, and that it maybe useful to select candidate genes using a combination of these methods, so as to capture genes that are interesting from different aspects.

Fig. 2.

Venn diagram showing the overlapping of significant features found by performing different methods on the stem cell data.

To further assess the top features lists produced by different methods, pathway analysis was done based on functional annotation clustering analysis using DAVID, which is available at http://david.abcc.ncifcrf.gov/home.jsp. Table 3 shows the results for the top features lists by our pooled correlation weighted method, RankProd (Hong et al., 2006) and GeneMeta (Choi et al., 2003). The first table shows the top pathways/functions for the 253 features that were selected by these three methods simultaneously. The next three tables show the top pathways/functions for the features that were selected by only one of the methods. We see that each method has its unique contributions of top functions, although the top functions for the pooled correlation weighted method and RankProd seem to be relatively more related, and they also seem to be more related to the top functions for the intersection of the three methods. The enrichment scores for the top functions by the pooled correlation weighted method and by RankProd also appear to be higher compared with GeneMeta. A higher enrichment score indicates that the top features lists contains features that aggregate into certain functions, as opposed to individual features that are unrelated. Thus, results with higher enrichment score may make more sense and be more easily interpretable.

Table 3.

Functional annotation clustering results (DAVID) for the top features lists by our pooled correlation weighted method, RankProd and GeneMeta

Top functions by the intersection of the three methods	Enrichment score
Extracellular region, signal peptide	4.65
Signal peptide, glycoprotein	3.04
Cell migration	2.63
Skeletal, face, head development	2.54
Cell adhesion	2.54
Extracellular matrix	1.91
Endochondral bone morphogenesis	1.64
Negative regulation of DNA binding	1.64
Blood vessel development	1.57
Top functions by pooled correlation weighted method only	Enrichment score
Blood vessel development	8.24
Embryonic development	6.15
Embryonic morphogenesis	5.44
Cell migration	5.01
Cell adhesion	4.71
Extracellular matrix	4.36
Regulation of cell migration	4.34
Mesenchymal cell development	4.21
Regulation of biosynthetic process and transcription	4.09
Tube and respiratory system development	3.42
Embryonic skeletal system development	3.4
Top functions by RankProd only	Enrichment score
Transcription regulation, zinc finger	9.96
Zinc finger	7.1
Tube and respiratory tube development	4.67
Positive regulation of transcription	4.4
Blood vessel development	4.2
Pattern specification process	4
Neuron development, cell morphogenesis	2.82
Negative regulation of transcription	2.77
Pathways in cancer	2.65
Sensory organ development	2.61
Top functions by GeneMeta only	Enrichment score
Nucleotide binding	5.18
Helicase, ATP binding	2.96
Protein localization	2.73
GTPase regulator activity	2.21
Hydrolase, protease	2.09
Metal-binding, zinc finger	2.01
Chromatin regulator	1.86

Since different methods have different assumptions and focus on different aspects in selecting significant features, it may be useful to use a combination of methods when doing meta-analysis for real data. Compared to GeneMeta, which relies heavily on assumptions of the distribution and structure of the data, and RankProd, which is less sensitive to inconsistent differential expression patterns across studies, our weighted method is a fast and convenient alternative that aims at selecting consistently differentially expressed genes without imposing too many assumptions on the data.

4 DISCUSSION AND CONCLUSIONS

While there have been many papers and methodologies written on the meta-analysis of high-dimensional genomic data, more recent efforts have focused on assessing reproducibility and concordance of these datasets. In this article, we have attempted to address these issues using the weighted hypothesis testing framework of Genovese et al. (2006). This seems very natural for our problem in that the weights represent relative measures of ‘strength of evidence’ for whether or not the data are combinable, and genes for which this assumption does not hold are down-weighted. The assumption weighting methodology itself is quite straightforward to implement; R scripts implementing the proposed methodology are available from the second author. While we have used Fisher's method for combining P-values, other methods for combining P-values could be used as well (Hedges and Olkin, 1985).

As pointed out by a reviewer, the correlation weights U_3g have a dependence structure due to the manner in which they are constructed. While we did not make any adjustment in the weighted multiple testing procedure for the dependence, we do not currently have a formal proof that using these weights will maintain control of the FDR. We leave this for future work.

The application of our methodology to the stem cell dataset found that there was substantial evidence of gene-specific heterogeneity across the datasets. One of the advantages of our methodology, relative to those of Miron et al. (2006) and Lai et al. (2007), is the assessment of local (i.e. gene-specific) heterogeneity, as opposed to the global heterogeneity assessment of those procedures. It appears that there is a bias-variance tradeoff between the two approaches and is something that we plan to investigate in future work.

Funding: National Institute of Health grants R01 GM72007 to D.G. and R01 CA129102 to D.G. and Y.L.

Conflict of Interest: none declared.