Abstract
Motivation: Pathway genes are considered as a group of genes that work cooperatively in the same pathway constituting a fundamental functional grouping in a biological process. Identifying pathway genes has been one of the major tasks in understanding biological processes. However, due to the difficulty in characterizing/inferring different types of biological gene relationships, as well as several computational issues arising from dealing with high-dimensional biological data, deducing genes in pathways remain challenging.
Results: In this work, we elucidate higher level gene–gene interactions by evaluating the conditional dependencies between genes, i.e. the relationships between genes after removing the influences of a set of previously known pathway genes. These previously known pathway genes serve as seed genes in our model and will guide the detection of other genes involved in the same pathway. The detailed statistical techniques involve the estimation of a precision matrix whose elements are known to be proportional to partial correlations (i.e. conditional dependencies) between genes under appropriate normality assumptions. Likelihood ratio tests on two forms of precision matrices are further performed to see if a candidate pathway gene is conditionally independent of all the previously known pathway genes. When used effectively, this is a promising approach to recover gene relationships that would have otherwise been missed by standard methods. The advantage of the proposed method is demonstrated using both simulation studies and real datasets. We also demonstrated the importance of taking into account experimental dependencies in the simulation and real data studies.
Contact: hhuang@stat.berkeley.edu; ljfeldman@berkeley.edu
Supplementary information:Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
A biological pathway is a series of chemical reactions that form an integral and critical part of every biological process. Pathway genes, or genes involved in the same biological pathway, constitute a fundamental functional grouping in a biological process. A major task in understanding biological processes is to identify a set of genes in the same biological pathways and elucidating the relationships between them.
Using gene expression data, there have been two popular computational approaches for finding pathway genes: clustering analysis and network models. Clustering analysis uses a co-expression measure to quantify similarities in gene expressions and then assigns similar genes into clusters (Eisen et al., 1998). Genes in each cluster are considered to be functionally related, and thus likely to be in the same pathway. This approach works when the pathway genes exhibit strong co-expressions with one another. Network models generally model a pathway as a network, with the genes represented as nodes and the gene relationships represented as edges linking the nodes, e.g. the work in Friedman et al. (2000). Starting with a full network, a typical pathway can be identified as a connected (sub)network after all the weak or insignificant edges are removed by a backward edge exclusion technique. Or alternatively, starting with an empty network, strong or significant edges can be added gradually to form a (sub)network using the method of forward inclusion of edges. Both have been widely used in literature to construct biological networks (Bolouri and Davidson, 2002; Butte and Kohane, 2000; De la Fuente et al., 2004; Dobra et al., 2004; Edwards, 1995; Lauritzen, 1996; Matsuno et al., 2006; Opgen-Rhein and Strimmer, 2007; Schäfer and Strimmer, 2005a, b; Wille et al., 2004).
The property of a network mainly relies on how to evaluate the edges between genes. There are two ways to assign edge weights. One is based on gene covariance matrix, which measures marginal similarity/correlation between any two genes. The other is based on inverse covariance matrix of genes, leading to a graph concerning conditional independence relationships. The latter is equivalent to using partial correlations as similarities.
Despite their appealing features, the approaches described above have limitations. One limitation comes from the high dimensionality of microarray data. The well-known large p, small n problem can result in an unreliable co-expression measure and hence a very high rate of false discoveries in clustering analysis. In the network models, this raises concern about the stability and accuracy of the model inference; it is almost impossible to employ the network models on a genomic scale as the estimation of covariance or its inverse matrices becomes problematic. Although there has been recent work such as regularized network models to overcome this problem (Schäfer and Strimmer, 2005a, b), the accuracy of the results remains unclear. As such, in practice, these approaches are usually applied to a rather small number of genes or among a small number of clusters of genes preselected based on some prior knowledge, which as a consequence, makes it difficult for us to explore the whole genomic scale of information.
Another concern is related to the limited biological inference of these approaches. Cluster methods are based on a marginal co-expression measure between two genes independent of other genes. Similarly in a network model using covariance matrix, an edge only connects genes with strong marginal correlations. Such approaches potentially expose us to the risk of missing higher level interactions such as group interactions, i.e. gene A interacts with a group of genes but it does not possess any strong relationship with the individual ones. This group interaction is frequently observed in real biological pathways when a group of genes cooperatively regulate one gene. Using the inverse covariance matrix of genes in a network model has a better hope for detecting such kinds of higher level interactions. The inverse covariance matrix is also known as the precision matrix, whose elements have an interpretation in terms of partial correlations (i.e. the correlation between any two genes conditioned on one or several other genes). However, in the current literature, partial correlation is mostly calculated conditioned on either all the available genes or a more-or-less arbitrary subset of them that likely contain noisy (i.e. non-pathway or biologically unrelated) genes. It is reported that conditioning on all genes simultaneously can introduce spurious dependencies which are not from a direct causal effect or common ancestors (De la Fuente et al., 2004). This problem may be circumvented to some extent by considering lower order partial correlations, e.g. calculating a partial correlation of two genes conditioned on every other individual variables (first-order partial correlation), and on every other two variables (second-order partial correlation) (De la Fuente et al., 2004; Magwene and Kim, 2004; Wille et al., 2004; Wille and Bühlmann, 2006). However, one concern on lower order partial correlation is its insensitivity for inferring higher level gene associations such as group interactions. More importantly, if the conditioned genes are biologically unrelated, the corresponding conditional dependence properties would be difficult to interpret and verifying the biological relevance of the recovered networks becomes challenging. Further discussions on the adverse effects of conditioning on noisy genes are given in Sections 2 and 3.
In this article, we introduce a new pathway gene search algorithm, designed based on evaluating partial correlations between genes, for a particular biological pathway of interest. The motivation of using partial correlation is based on its ability to detect complex gene relationships under appropriate normality assumptions of the data: (i) a strong partial correlation between two genes suggests a direct interaction despite a weak marginal correlation; (ii) a negligible partial correlation suggests no direct relationship after removing influences from other genes and the two genes are conditionally independent. To overcome the concerns and limitations of current methods for using partial correlations, we require a few (e.g. 3–5) preselected biologically related pathway genes, upon which the partial correlation is conditioned on, to guide the search. Specifically, we perform the likelihood ratio tests to see if a candidate gene is conditionally independent of all the preselected known pathway genes. The requirement of pre-known pathway genes seems a limitation of our approach. However, by incorporating this small amount of biological knowledge, huge advantages on biological inference can be gained and false positive discoveries have been reduced dramatically (Section 3). Furthermore, by conditioning on preselected pathway genes, the resulting partial correlation coefficients can be directly interpreted as a similarity measure to the considered pathway. In addition to suggesting satisfying mathematical and biological properties, the proposed approach is also advantageous computationally since we only need to estimate a moderate dimensional precision matrix once for each candidate gene.
Moreover, we also take into account the presence of experiment dependencies in the gene expression data when estimating a precision matrix [elements in a precision matrix are proportional to partial correlations between genes (Schäfer and Strimmer, 2005a)]. In current studies of gene relationships, the presence of expression dependencies attributable to the biologically interrelated experiments has been widely ignored. When unaccounted for these (experiment) dependencies can result in inaccurate inferences of functional gene relationships, and hence incorrect biological conclusions (Teng and Huang, 2009). Our simulation and real data study supports this conclusion and confirms that considering those dependencies indeed plays a critical role in correctly inferring pathway gene relationships.
The rest of the article is organized as follows. In the Section 2, we introduce the mathematical and statistical background of our approach. In Section 3, we demonstrate the model validity and evaluate the performance of our approach using extensive computer simulations and real data applications. In real data applications, we apply it to genomic scale Arabidopsis thaliana datasets obtained from four different types of environmental stresses (oxidation, wounding, UV-B light and drought). We examine the effects of these stresses by focusing on the genes associated with the glucosinolate (GSL) and flavonoid biosynthesis (FB) pathways. Finally, we discuss the advantages as well as potential drawbacks of our framework and consider further directions for research.
2 METHODS
As we discussed earlier, in contrast to marginal calculation (e.g. the Pearson correlation), partial correlation can work as a more effective tool for inferring complex gene interactions in pathways when it is properly computed. Below, we first provide a brief review on the concept of partial correlation, followed by a detailed description of a new search strategy, designed based on a likelihood ratio test on partial correlations, for finding pathway genes.
2.1 Partial correlation
When an expression matrix (with genes in rows and experimental conditions in columns) is multivariate normally distributed, standard graphical model theory (Edwards, 1995) shows that the partial correlation between genes can be equivalently represented by the corresponding elements in the precision matrix (ΣG)−1 , where ΣG is the covariance matrix. That is, for a set of genes W, the partial correlation between genes i and j can be expressed as
 |
(1) |
where ωij are elements in the inverse gene covariance (or inverse gene correlation) matrix (Edwards, 1995; Schäfer and Strimmer, 2005a). With the normality assumption on expression measurements, when ρij vanishes, two genes i and j are conditionally independent given the remaining genes.
2.2 Method motivation
A negligible element in the precision matrix suggests conditional independence between two genes. This motivates us to use precision matrix as a key component in our method for detecting higher level gene interactions, e.g. group gene interactions in a pathway. However, the successful use of partial correlation highly relies on two issues. One issue is about the selection of a proper set of genes upon which the correlation is conditioned on, i.e. W\i,j in formula (1). When this set of genes contains noisy (i.e. non-pathway) genes, the derived partial correlation would be unreliable for detecting gene relationships. We can see this explicitly through a linear regression interpretation of partial correlation: the partial correlation ρij between gene i and gene j conditioned on a set of genes Z is simply the correlation cor(ε1, ε2) of the residuals ε1 and ε2 resulting from linearly regressing gene i and gene j against the genes in Z, respectively. Assume we have pre-known pathway genes x and y, and a non-pathway gene h that is independent of genes x and y in Z. Now we consider two candidate genes u=x+y and v=δ(x+y)+h (note that these two equations only represent the expression relationship between the genes), where δ is small and close to 0. Clearly, u is more likely to be a pathway gene due to its direct and strong relationship with two pre-known pathway genes x and y, while v is more likely to be a non-pathway gene since it is almost a replicate of the non-pathway gene h. However, the partial correlations cor(u, x|Z\{x})=cor(v,x|Z\{x})=cor(u, y|Z\{y})=cor(v, y|Z\{y})=1, showing no advantages of gene u over gene v for their partial correlations with the pathways genes x and y. This undesired performance is due to the inclusion of noisy genes in the gene set Z upon which the partial correlation was computed. Recognizing this, we decide to build up our approach by conditioning only on a small set of pre-known pathway genes to reduce noise in partial correlation estimation. We call this set of pre-known pathway genes as seed genes. Though the requirement of seed genes seems a limitation, only 3–5 seed genes are really needed for our method to run and generate reliable results. In brief, by incorporating a small amount of prior biological information, we can gain huge advantages in detecting genes involved in a particular pathway (Section 3). Furthermore, in Section 3, by using both simulation and real data, we additionally demonstrate the adverse effects of having noisy genes in the set of seed genes in detecting pathways genes. The other issue critical to the proper use of partial correlation is on the estimation of gene precision matrix [see Formula (1)]. Given a gene expression matrix with genes in rows and experiments in columns, an effective estimation of gene precision matrix is challenging especially when there are experiment dependencies (or when the row-wise and column-wise dependencies co-exist) in the original gene expression. Experiment dependencies can be defined as the dependencies in gene expression between experiments due to the similar or related cellular states induced by the experiments (Teng and Huang, 2009). Such dependencies cause dependent elements in a gene expression vector. When unaccounted for, they can result in inaccurate inferences of gene relationships, and hence incorrect biological conclusions. To take into account the experiment dependencies in partial correlation estimation, we adapt a model and an estimation procedure, named Knorm from Teng and Huang (2009), for inferring gene correlation matrix when there are both the gene-wise and experiment-wise dependencies in the gene expression matrix. The main aspect of the framework is the use of a Kronecker product covariance matrix to model the gene–experiment interactions. The Knorm estimation is mainly achieved by an iterative estimation of the two covariance matrices: one covariance matrix is estimated through a weighted correlation formula assuming the other covariance matrix is known. In addition, a row subsampling technique (to enable a comparable number of rows and columns in estimation) and a covariance shrinkage technique (to stabilize the estimated covariance matrices) are employed to ensure a robust estimation. Compared with the Pearson coefficient, the Knorm correlation has a smaller estimation variance when experiment dependencies exist. More details of incorporating Knorm in our estimation procedure are presented in next section.
2.3 Likelihood ratio tests for pathway gene search
Let S={g1,…, gk} denote the set of seed genes for a pathway of interest and G denote the set of all genes whose expression measurements in T experiments (each experiment may have > 1 replicates) are available. Usually |G|≫|S|=k and T > |S|. Motivated by the arguments in the above section, we formulate a searching strategy, based on performing likelihood ratio tests, for pathway genes as follows.
We first estimate the experiment correlation matrix ΣE using the Knorm R package provided by Teng and Huang (2009). The input data are the expression measurements of the |G| genes in T experiments, and there are > 1 replicated samples for each experiment. To generate expression matrices, we randomly choose one replicate from each experiment to compose a sample matrix Xb of dimension |G|×T and by repeating this process, we generate B sample matrices X1,…, XB with B large enough. By the model in Teng and Huang (2009), Xb is considered to be generated from a multivariate normal distribution with mean M (a matrix of dimension |G|×T) and a covariance matrix ΣG ⊗ ΣE, where ΣG represents the gene covariance matrix and ΣE is the experiment correlation matrix. The output of the Knorm R package is the estimated M and ΣE, denoted as
and 
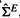, by an iterative estimation procedure. More details on the Knorm estimation procedure can be found in (Teng and Huang, 2009).- For a candidate gene gc∈G\S (S is the set of k seed genes), we estimate the gene covariance matrix for genes in S∪gc by
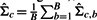, where
Xc,b represents one of the sample matrices [of dimension (k+1)×T] constructed by bootstrapping the replicates of each experiment for the expression measurements of the genes in S∪gc (the first k rows correspond to the k seed genes and the row k+1 corresponds to the candidate gene gc).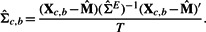
(2) - Obtain the precision matrix,
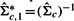. Note that we usually require T> 1.5k so that 
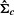is usually invertible. When 
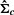is not invertible, we use its pseudo inverse. 
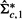will be used as an approximate Maximum Likelihood Estimate (MLE) of the precision matrix under the alternative model in Equation (3). We further write
where ai,j=aj,i for i=1,…, k+1 and j=1,…, k+1.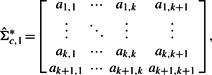
- Obtain matrix
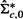from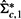 
by replacing the offdiagonal elements in the bottom row and rightmost column of 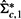by zeros. That is,
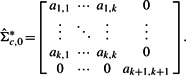
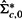will be used as an approximate MLE of the precision matrix under the null hypothesis in Equation (3). - Perform the following hypothesis test
where Ω0 is the collection of precision matrices (for the genes in S∪gc) with zero offdiagonal elements in the bottom row and rightmost column, and Ω is the collection of all possible precision matrices. The null hypothesis assumes conditional independence between the candidate gene and each of the seed genes given all other seed genes. Then the test statistic is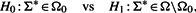
where L(·) and l(·) denote the likelihood and the log-likelihood function, respectively. When a candidate gene has no relationship with the pathway seed genes, the corresponding elements in a precision matrix will be close to zeros (i.e. null is true and the test statistic will be small). In contrast, if a candidate gene has a significant association with the pathway genes, those values will be far from zero and naturally the test statistic will be large and declared as significant under the test.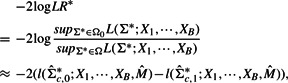
(3) Repeat steps (ii)–(v) for all candidate genes in G\S. Given the test statistic values for all the candidate genes, we rank them in decreasing order. It is a natural interpretation that the higher a candidate gene is ranked in the list, the more likely that gene is associated with the seed genes. Based on the list, we can decide how many of them should be declared as pathway genes using statistical thresholds (see Supplementary Material for p-value calculations) and/or biological cutoff. We call this method as pwsrc.knorm.
If there are questions on which known pathway genes to include as seed genes or on which expression datasets to use, an optional method is to repeatedly run pwsrc.knorm to derive a set of frequently identified pathway genes under different datasets with different possible sets of seed genes tried (Supplementary Material for details). The candidate pathway genes identified this way would be robust against the change of data and the choice of seed genes.
2.4 Other methods for comparison
For performance comparison, four additional methods, pwsrc.null, pearson.mean, pearson.max and GLM are considered. The first pwsrc.null is designed by replacing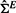 
in Equation (2) with the identity matrix to represent the case ignoring experiment dependencies. pearson.mean and pearson.max adopt the Pearson correlation as a distance measure. Specifically, they calculate pair-wise correlation coefficients between each candidate gene and the seed genes and take either mean (pearson.mean) or maximum (pearson.max) of them. GLM adopts the regression model of the candidate gene gc on the seed genes in S as follows:
 |
(4) |
where ε is assumed to be normally distributed with zero mean. Since a negligible residue implies a possible interaction between the candidate gene and the seed genes, naturally we can use the residuals as our test statistics (all the genes are scaled to have unit norm before doing regression analysis). For a fair comparison with our method, the experiment dependencies in the gene expression are removed by projecting the data matrix onto the eigenspace of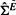 
by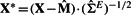 
.
3 RESULTS
We evaluate the performance of the proposed method in identifying pathway genes using simulation data and real microarray datasets. In both studies, we calculated precision = TP/(TP+FP) and recall = TP/(TP+FN) to assess the results from our approach and several other methods mentioned in Section 2. Here TP is the number of true positive findings of pathway genes, FP is the number of false positives and FN is the number of false negatives. Note that precision and recall are popular measures for evaluation of classification performance. In the context of this study, they can be regarded as a measure of exactness and completeness of our pathway gene searching results, respectively. In the real data analysis, we will present the strength and usefulness of our approach as a tool for identifying pathway genes, particularly in glucosinolate (GSL) and flavonoid biosynthesis (FB) pathways. In our study, the pathway genes are defined as composed of structural genes that encode an enzyme, whereas regulator genes are defined as genes controlling the expression of the structural genes.
3.1 Simulation study
We simulate a microarray dataset consisting of 500 genes and 30 experiments, with 5 replicates for each experiment. To make the approach more realistic, we introduce experiment dependencies, multiple distinct pathways and some random noise into the simulated data. The simulation parameters are as follows:
Experiment correlation matrix, ΣE. This matrix characterizes the experiment dependencies. For illustrative purposes, we set the experiment correlation matrix to have various dependencies such as 10, 33, 50 and 67%. In the case of a 33 dependency, for example, ~33% of the experiments have high dependencies while the remaining experiments are uncorrelated with one another, i.e. the first 10×10 elements in ΣE lie between 0.5 and 0.6, with the rest being zeros. Diagonals on ΣE are set to 1. Figure 1 shows the heatmaps for three of the four experiment correlation matrices mentioned above.
Gene covariance matrix, ΣG. This matrix characterizes the gene dependencies among one another. As an illustrative example, we introduce two distinct pathways with 15 genes in each pathway; genes in the same pathway have high correlation while genes not in the same pathway are uncorrelated. Specifically, in each pathway the first four genes designated to be seed genes show high correlation (correlation coefficient changes between 0.5 and 0.6) between each other. The remaining 11 genes are separated into three subgroups and are designed to have high correlation with 1, 2 or 4 of the seed genes, respectively, and low correlation with the others (correlation coefficient changes between 0.1 and 0.2).
Fig. 1.
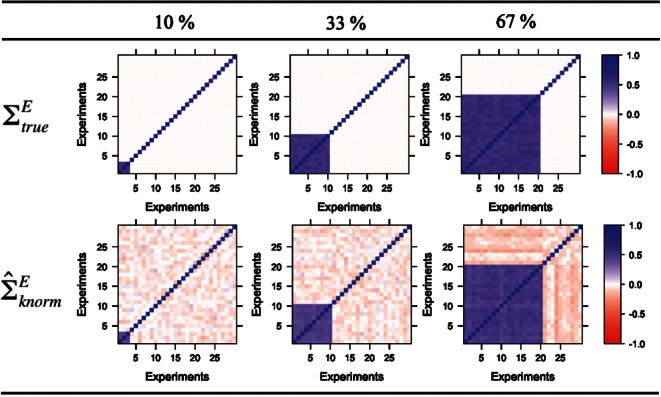
Heatmaps of (Top) true and (Bottom) estimated experiment correlation matrices of the simulation datasets having different experiment dependencies (10, 33 and 67%).
The simulated data is generated as follows. First, we generate a 500×30 gene expression matrix X, with vec(XT), from a multivariate normal distribution with mean X (zero matrix) and a covariance matrix ΣG ⊗ ΣE. To make the pathway genes more realistic, for each pathway two randomly chosen genes in each subgroup are linearly combined to make a new pathway gene. The same procedure generated all the final 11 pathway genes for each pathway (replacing the original 11 pathway genes generated above). Using the final 500×30 gene expression matrix, we add random noise with a small SD (e.g. 0.01) to each column (i.e. experiment) to generate the 5 replicates for each experiment. Repeating this process, we generate 1000 simulation datasets.
In this analysis, we compare our approach to that of others and evaluate the performance using precision and recall measures. All the approaches are implemented as follows: given seed genes, run the pathway search algorithms as described in Section 2 and rank the genes by their measured relationships to the seed genes. Calculate precision and recall for the top n (i.e, n = 1,…, 15) genes.
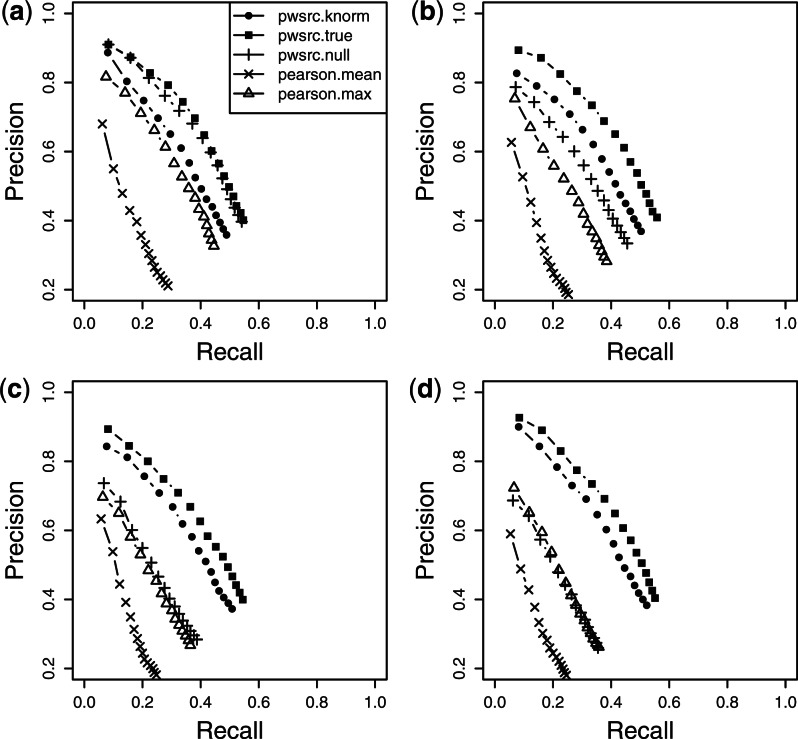
As this is a simulation study and we know the true experiment correlation matrix, we add one more method pwsrc.true into the comparison. The only difference between pwsrc.true and pwsrc.knorm is that pwsrc.true uses the true experiment correlation matrix (ΣEtrue) instead of the estimated one in Equation (2). We denote the estimated correlation matrix used by our method as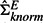 
for clarity. The results are summarized in Figure 2. When the dependencies among experiments are low, pwsrc.knorm performs worse than pwsrc.null. However, this performance discrepancy becomes smaller as the experiment dependency increases and finally pwsrc.knorm outperforms pwsrc.null when the experiment dependency exceeds 33%. This situation can be easily understood in Figure 1. When the dependencies among experiments are low, the noisy signals in the offdiagonal elements in 
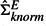become non-negligible and so ΣEnull becomes a better estimate for ΣEtrue even though it totally misses capturing the experiment dependencies. However, when the experiment dependency increases up to 33%, 
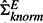estimates ΣEtrue better than ΣEnull as it is critical to capture the dependent structure now. These results emphasize the importance of considering experiment dependencies when they exist at a non-negligible level in data, which is actually the case in real applications. Our approach overall achieves higher precision and recall than pearson.mean and pearson.max (Fig. 2), whereas the GLM method provides about the same result as our method due to the way we simulated the data (results are not shown here).
Fig. 2.
Graphical summary of the simulation study. Simulation datasets are generated with different experiment dependencies (a) 10%, (b) 33%, (c) 50% and (d) 67%. For each plot, precision and recall are calculated from the top n (n=1,…, 15) genes in the list obtained by five different methods.
To determine the importance of the seed gene quality, we added two randomly chosen, non-pathway genes into the seed-gene-set which is originally composed of four pathway genes. The results are summarized in Supplementary Figure S1. Regardless of the experiment dependencies, the performance of pwsrc.knorm becomes worse when the seed-gene-set contains noisy genes.
3.2 Application to real datasets
We next test the validity of our approach by applying it to biological pathways composed of genes that are known to operate in tandem. For this test set, we selected two secondary metabolic pathways from the model plant A.thaliana: the pathway leading to GSLs, sulfur-rich amino acid-containing compounds which become active in response to tissue damage, and believed to offer a protective function (Hammond-Kosack and Jones, 2001; Sønderby et al., 2010; Verkerk et al., 2009; Yan and Chen, 2007), and the pathway leading to flavonoids, compounds of diverse biological activities such as anti-oxidants, functioning in UV protection, in defense, in auxin transport inhibition, and in flower colouring (Gachon et al., 2005; Naoumkina et al., 2010; Taylor and Grotewold, 2005; Woo et al., 2005). In Arabidopsis, the regulators and structural genes in glucosinolate (GSL) and flavonoid biosynthesis (FB) pathways have been extensively characterized. A considerable number of genes in both pathways are induced by broad environmental stresses, and regulated at the transcriptional level. Furthermore, several research groups have applied transcriptome co-expression to analyze the two pathways (Gachon et al., 2005; Hirai et al., 2007; Yonekura-Sakakibara et al., 2008), thus providing us with a rich source of data for validating our results.
Known genes in each pathway were selected and their conditional dependencies examined using the approach outlined in Section 2. For this effort, we used public ATH1 microarray datasets from the AtGenExpress consortium (www.arabidopsis.org/portals/expression/microarray/ATGenExpress.jsp). Among stress serial microarray experiments, we selected four datasets for analysis. A summary of the experimental sets used is listed in Table 1, whereas a detailed description of their experimental parameters is provided in Supplementary Table S1. We then asked, under these varied conditions whether we could recover these known pathway genes by our approach. Finally, having investigated the validity of this approach, and demonstrating that our approach is much more effective than any previous approaches for detecting the known pathway genes, we asked whether we could identify other possible candidate pathway (new) genes. Initially, we investigated the two pathways gene sets in shoot tissue only, but then later expanded the study to include root tissue.
Table 1.
Description of the A.thaliana microarray datasets with four different types of stress
| Oxidation | Wounding | UV-B light | Drought | |
|---|---|---|---|---|
| Data counts (biosamples/replicate sets) | 52 (26/26) | 60 (30/30) | 60 (30/30) | 60 (30/30) |
| Number of genes | 22 810 | 22 810 | 22 810 | 22 810 |
| Experimental variables | MVa, time, shoot, root | Wounding, time, shoot, root | UV-B lightb, time, shoot, root | Drought, time, shoot, root |
| Submission number | ME00340 | ME00330 | ME00329 | ME00338 |
aMethyl viologen.
bUV-B light: ultraviolet radiation with a range of 280–320 nm.
3.2.1 Studies on GSL pathway
Based on an extensive literature search, we determined 64 genes that can be associated with the GSL pathway (Supplementary Table S2). These 64 genes include, in addition to core genes involved in GSL biosynthesis, regulators of this biosynthesis, early steps of side chain elongation/modification and late steps of catabolism (Supplementary Fig. S2 in detail). For our study, two seed-gene-sets are proposed: (i) seed-gene-set I: AT5G60890 (ATR1), AT4G39950 (CYP79B2), AT2G20610 (SUR1), AT4G31500 (CYP83B1) and (ii) seed-gene-set II: AT5G60890 (ATR1), AT5g07690 (MYB29), AT5g61420 (MYB28), AT4G39940 (AKN2). In seed-gene-set I, only ATR1 encodes a transcription factor (TF), whereas three other genes encode enzymes. In contrast to seed-gene-set I (composed of the core pathway genes), seed-gene-set II is composed of four regulatory genes (Supplementary Fig. S2).
Using two seed-gene-sets, we first analyzed only the shoot tissue dataset from tissues subjected to oxidative stress. This dataset is composed of 22 810 genes and 13 experiments with two biological replicates for each experiment. The number of identified GSL pathway genes is summarized in Table 2(a)–(b) for the top 10, 20, 30 and 50 genes from the list obtained by pwsrc.knorm, pwsrc.null, pearson.mean, pearson.max and GLM. With seed-gene-set I in Table 2(a), pwsrc.knorm works best, finding 4, 6, 7 and 8 pathway genes out of the top 10, 20, 30 and 50 genes, respectively. With seed-gene-set II in Table 2(b), a significant increase is observed in the number of identified pathway genes, especially for pwsrc.knorm. For example, among the top 30 genes in the list, pwsrc.knorm finds 7 more pathway genes, while pwsrc.null, pearson.mean, pearson.max and GLM find 2, 2, 1 and 4 more genes compared to Table 2(a), respectively. This increase demonstrates that seed-gene-set II indeed carries more influential information than seed-gene-set I, which enables us to examine the GSL pathway more thoroughly. Furthermore, our method pushes the pathway genes to rank higher positions in the list so that the final precision becomes 60, 55 and 47%, respectively, for the top 10, 20 and 30 genes.
Table 2.
The number of identified GSL pathway genes in the A.thaliana microarray dataset from tissues subjected to oxidative stress using (a) shoot tissue only, seed-gene-set I; (b) shoot tissue only, seed-gene-set II; (c) shoot and root tissues, seed-gene-set I; (d) shoot and root tissues, seed-gene-set II
| Top | pwsrc.knorm | pwsrc.null | pearson.mean | pearson.max | GLM | |
|---|---|---|---|---|---|---|
| (a) | 10 | 4 | 0 | 2 | 1 | 0 |
| 20 | 6 | 1 | 3 | 4 | 0 | |
| 30 | 7 | 1 | 3 | 5 | 0 | |
| 50 | 8 | 1 | 4 | 7 | 0 | |
| (b) | 10 | 6 | 0 | 4 | 2 | 2 |
| 20 | 11 | 3 | 4 | 4 | 3 | |
| 30 | 14 | 3 | 5 | 6 | 4 | |
| 50 | 14 | 5 | 8 | 8 | 5 | |
| (c) | 10 | 9 | 0 | 3 | 0 | 3 |
| 20 | 11 | 0 | 3 | 0 | 5 | |
| 30 | 12 | 0 | 3 | 1 | 7 | |
| 50 | 12 | 0 | 3 | 2 | 10 | |
| (d) | 10 | 6 | 0 | 5 | 1 | 4 |
| 20 | 10 | 0 | 7 | 1 | 5 | |
| 30 | 13 | 0 | 9 | 1 | 9 | |
| 50 | 19 | 0 | 9 | 1 | 12 | |
Next, the dataset is expanded to include the root tissue as well, so now the dataset consists of 26 experiments with two replicates each. Again, the combined dataset is analyzed with the two seed sets as above and the results are summarized in Table 2(c)–(d). For pwsrc.knorm, a dramatic increase is observed with the seed-gene-set I [compare Table 2(a) and (c)], in contrast to the seed-gene-set II [compare Table 2(b) and (d)]. This finding emphasizes the importance of designing the seed-gene-set. When the seed set is appropriately designed for the pathway of our interest, i.e. seed-gene-set II, pathway searches could proceed more efficiently with a smaller set of data, but if not, more information (a larger dataset) would be needed to achieve the same performance. pwsrc.null finds no pathway genes in this data, which demonstrates the importance of considering experiment dependency, especially as the dataset dimension expands. Different to pwsrc.null and the Pearson correlation-based measures, GLM shows a prominent increase, and we believe that the extra information added by the root tissue helps GLM perform better. The graphical summary of Table 2 is given in Supplementary Figure S3. For each method, precision and recall are calculated for the top 10, 20, 30, 50 and 100 gene lists and plotted accordingly.
In contrast to and different from the oxidative stress, wounding stress is known to induce the expression of MYB28 and MYB29 (Gigolashvili et al., 2009), which are the two of four seed genes in seed-gene-set II and which regulate Met-derived GSL biosynthesis. Based on our success in finding additional GSL pathway genes using seed-gene-set II and oxidative stress as the environmental input, we predicted that we would have similar success using wounding as the environmental input. We expected under wounding stress conditions, that structural genes in the GSL pathway would have stronger association with seed-gene-set II than under oxidative stress condition. Data from the shoot only subjected to wounding are first analyzed by considering 22 810 genes, and 15 experiments, each with two biological replicates. The results are summarized in Table 3(a)–(b). Again, a significant increase in the number of identified pathway genes is observed from seed-gene-set I [Table 3(a)] to seed-gene-set II [Table 3(b)]. Next, the dataset from the root portion is also included, now comprising 30 experiments in total, with two biological replicates for each experiment. No matter what seed-gene-set we use, pwsrc.knorm works best [Table 4(c)–(d)]. The precisions for the top 10, 20 and 30 ranked genes are 100, 70, 50% with the seed-gene-set I, and 90, 65, 60% with the seed-gene-set II. It is also noteworthy that with seed-gene-set I and II, pwsrc.knorm finds 10 and 9 genes to be in the same biological pathway from the top 10 genes, respectively. A graphical summary of Table 3 is given in Supplementary Figure S4. The performances in the analysis of the last two A.thaliana microarray datasets from plants subjected to UV-B light and drought stresses are about the same, compared to the previous results with oxidative and wounding stresses (summarized in Supplementary Tables S3 and S4, respectively, and the corresponding graphical summaries are also provided in Supplementary Figs S5 and S6).
Table 3.
The number of identified GSL pathway genes in the A.thaliana microarray dataset from tissues subjected to wounding stress using (a) shoot tissue only, seed-gene-set I; (b) shoot tissue only, seed-gene-set II; (c) shoot and root tissues, seed-gene-set I; (d) shoot and root tissues, seed-gene-set II
| Top | pwsrc.knorm | pwsrc.null | pearson.mean | pearson.max | GLM | |
|---|---|---|---|---|---|---|
| (a) | 10 | 3 | 1 | 2 | 3 | 0 |
| 20 | 4 | 1 | 2 | 3 | 0 | |
| 30 | 4 | 1 | 3 | 3 | 0 | |
| 50 | 4 | 1 | 3 | 6 | 0 | |
| (b) | 10 | 4 | 0 | 6 | 4 | 0 |
| 20 | 8 | 0 | 9 | 5 | 1 | |
| 30 | 11 | 2 | 13 | 5 | 1 | |
| 50 | 12 | 5 | 15 | 8 | 1 | |
| (c) | 10 | 10 | 3 | 3 | 0 | 6 |
| 20 | 14 | 4 | 3 | 1 | 10 | |
| 30 | 15 | 5 | 3 | 1 | 12 | |
| 50 | 16 | 5 | 3 | 2 | 14 | |
| (d) | 10 | 9 | 0 | 6 | 0 | 7 |
| 20 | 13 | 0 | 7 | 0 | 8 | |
| 30 | 18 | 0 | 8 | 0 | 10 | |
| 50 | 22 | 2 | 10 | 1 | 16 | |
Table 4.
The number of pathway genes identified from FB and phenylpropanoid biosynthesis pathways by (a) seed-gene-set III and (b) seed-gene-set IV in the A.thaliana microarray dataset from shoot and root tissues subjected to drought stress
| Top | pwsrc.knorm | pwsrc.null | pearson.mean | pearson.max | GLM | |
|---|---|---|---|---|---|---|
| (a) | 10 | 6 (2) | 0 | 0 | 2 | 4 (1) |
| 20 | 9 (3) | 1 | 0 | 3 | 5 (1) | |
| 30 | 10 (3) | 1 | 0 | 4 | 6 (2) | |
| 50 | 11 (3) | 1 | 0 | 4 | 6 (2) | |
| (b) | 10 | 6 (2) | 2 | 1 | 4 | 5 (1) |
| 20 | 9 (3) | 2 | 2 | 4 | 5 (1) | |
| 30 | 10 (3) | 2 | 2 | 4 | 6 (2) | |
| 50 | 13 (4) | 2 | 2 | 4 | 6 (2) | |
For complete results, see Supplementary Table S6. The number of identified genes from phenylpropanoid pathways is designated in the parenthesis adjacent to the total number of identified genes.
3.2.2 Studies of the FB pathway
The flavonoid pathway is derived from the upstream phenylpropanoid pathway, beginning at coumaroyl-CoA (Supplementary Fig. S7). Based on an extensive literature search, we found that at least 26 genes can be associated with the FB pathway (Supplementary Table S5). Genes encoding enzymes in this pathway are regulated by at least 12 TFs belonging to different families, including bZIP WD40, WRKY, MADS-box, R2R3-MYB, and the basic helix–loop–helix (bHLH) family (Yonekura-Sakakibara et al., 2008). It is also worth noting that the genes we considered for the two pathways (GSL and flavonoid) are exclusive to each other, and thus there is no overlap in the genes of the pathways we consider.
It is reported that structural genes (encoding enzymes) in the FB pathway are regulated at the transcriptional level, suggesting that the regulation genes would be good candidates as seed genes, as indicated by the result of GSL pathway study in Section 3.2.1. Then we selected two different seed-gene-sets from four different types of TFs [AT4G09820 (TT8), AT5G23260 (TT16), AT5G24520 (TTG1), AT2G37260 (TTG2)] and one structural gene [AT5G08640 (FLS)]: (i) seed-gene-set III: AT4G09820 (TT8), AT5G23260 (TT16), AT5G24520 (TTG1), AT5G08640 (FLS) and (ii) seed-gene-set IV: AT4G09820 (TT8), AT5G23260 (TT16), AT2G37260 (TTG2), AT5G08640 (FLS).
In this FB pathway study, we present the results using both shoot and root tissues. The number of genes identified by seed-gene-set III and IV using four different datasets is similar, with the results from drought stress summarized for brevity in Table 4 (see Supplementary Table S6 for the complete results). Overall, pwsrc.knorm outperforms other methods regardless of seed-gene-sets and stress types. It is worth noting that both seed-gene-sets detected several genes from the upstream phenylpropanoid pathway by pwsrc.knorm and GLM. To elucidate the cooperative nature of these pathways, we designate the number of identified genes from the upstream pathways (phenylpropanoid pathway) in the parenthesis adjacent to the total number of identified genes (Table 4). For example, the dataset with drought stress 33% (by pwsrc.knorm), and 20% (by GLM) of the identified genes from top 20 derive from the upstream pathways. Supplementary Table S7 lists all the identified drought stress pathway genes from the top 20 list, and designates the original pathway to which each gene belongs. In Supplementary Figure S7, all the identified genes in Table 4 by pwsrc.knorm are visualized. It is noteworthy that pwsrc.knorm not only detects six core genes [AT3G51240 (F3H), AT3G55120 (CHI), AT5G13930 (CHS), AT5G07990 (F3′H), AT5G17050 (UGT78D2), AT1G78570 (RHM1)] in the FB pathway, but additionally finds three more genes, AT1G65050 (4CL3), AT2G23910 (CCR6) and AT2G37040 (PAL1), located at the branch points of phenylpropanoid pathway to the FB pathway or to the lignin biosynthesis pathway at coumaroyl-CoA (Supplementary Fig. S7). Among those additionally found genes, CCR6 and PAL1 are uniquely detected by our method. Thus, in contrast to, and differing from the other methods, pwsrc.knorm enables us to find additional genes from closely related pathways by considering the indirect relationships between genes. This finding can be useful for future studies targeted to discovering the cooperative nature of genes in the FB pathways.
We also compared our results with the seed-gene-sets containing some noisy genes. For example, we applied our method to the dataset with drought stress with the seed-gene-set composed of seed-genes-set III and two of GSL pathway genes. As summarized in Supplementary Table S8, the number of pathway genes identified decreased which implies that the pathway gene search becomes less efficient when the seed-gene-set contains noisy genes not biologically related to the pathway of our interest.
Finally, we compared our results with other literatures on the discovery of GSL and FB pathway genes. See the Supplementary Material for details.
4 DISCUSSION
We have proposed a novel approach to identify genes associated with a pathway specified by a set of seed genes. This approach considers the space of pathway genes as a span generated by its pathway genes and uses partial correlation as a distance measure to determine genes interacting with the previously identified pathway genes. This approach differs from many existing approaches in the following aspects: (i) it uses the partial correlation conditioned upon identified pathway genes, not on all genes; (ii) it enables us to identify genes having higher level interaction (i.e. group interaction) although their pair-wise marginal correlations are weak; (iii) it considers experiment dependencies when inferring gene relationships; (iv) its computational workload is less demanding.
The first aspect above implies our method is pathway specific. It focuses its search only on a particular pathway among all existing multiple (unknown) pathways in a dataset. This is a limitation of our approach. But we note that this specific search has shown huge advantages in reducing false positive discoveries in both our simulation and real data studies, and has also led to a deeper and insightful biological interpretation of the results. This approach can potentially be extended to the situation that the seed genes or target pathways are not available, if the seed genes for different pathways can be originated from analysis of other sources of biological data.
Although our approach has yielded encouraging biological results in a real dataset application, there is still room for further improvement, including exploration of properties of this approach to answer questions like, ‘What are the biological properties of the identified genes?’ and, ‘How reliable is the set of identified genes?’. Further biological understanding of the identified pathway genes would give us deeper insights into the biological process under consideration.
Funding: National Institutes of Health, National Eye Institute (R21EY019094 to H.H.) in part.
Conflict of Interest: none declared.
Supplementary Material
REFERENCES
- Bolouri H., Davidson E.H. Modeling transcriptional regulatory networks. BioEssays. 2002;24:1118–1129. doi: 10.1002/bies.10189. [DOI] [PubMed] [Google Scholar]
- Butte A.J., Kohane I.S. Mutual information relevance networks: Functional genomic clustering using pairwise entropy measurements. Pac. Sympos. Biocomput. 2000;24:418–429. doi: 10.1142/9789814447331_0040. [DOI] [PubMed] [Google Scholar]
- De la Fuente A., et al. Discovery of meaningful relationships in genomic data using partial correlation coefficients. Bioinformatics. 2004;20:3565–3574. doi: 10.1093/bioinformatics/bth445. [DOI] [PubMed] [Google Scholar]
- Dobra A., et al. Sparse graphical models for exploring gene expression data. J. Multivar. Anal. 2004;90:196–212. [Google Scholar]
- Edwards D. Introduction to Graphical Modeling. Springer-Verlag New York, Inc.; 1995. [Google Scholar]
- Eisen M.B., et al. Cluster analysis and display of genome-wide expression patterns. Proc. Natl Acad. Sci. USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman F., et al. Using Bayesian networks to analyze expression data. J. Comput. Biol. 2000;7:601–620. doi: 10.1089/106652700750050961. [DOI] [PubMed] [Google Scholar]
- Gachon C.M.M., et al. Transcriptional co-regulation of secondary metabolism enzymes in Arabidopsis: functional and evolutionary implications. Plant Mol. Biol. 2005;58:229–245. doi: 10.1007/s11103-005-5346-5. [DOI] [PubMed] [Google Scholar]
- Gigolashvili T., et al. The plastidic bile acid transporter 5 is required for the biosynthesis of methionine-derived glucosinolates in arabidopsis thaliana. Plant Cell. 2009;21:1813–1829. doi: 10.1105/tpc.109.066399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammond-Kosack K., Jones J.D.G. Responses to plant pathogens. In: Buchanan B.B., et al., editors. Biochemistry and Molecular Biology of Plants. Rockville: American Society of Plant Physiologists; 2001. pp. 1114–1115. [Google Scholar]
- Hirai M.Y., et al. Omics-based identification of Arabidopsis Myb transcription factors regulating aliphatic glucosinolate biosynthesis. Proc. Natl Acad. Sci. USA. 2007;104:6478–6483. doi: 10.1073/pnas.0611629104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauritzen S. Graphical models. Oxford: Clarendon Press; 1996. [Google Scholar]
- Magwene P.M., Kim J. Estimating genomic coexpression networks using first-order conditional independence. Genome Biol. 2004;5:R100. doi: 10.1186/gb-2004-5-12-r100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuno T., et al. Graphical gaussian modeling for gene association structures based on expression deviation patterns induced by various chemical stimuli. IEICE Trans. Inf. Syst. 2006;E89D:1563–1573. [Google Scholar]
- Naoumkina M.A., et al. Genome-wide analysis of phenylpropanoid defence pathways. Mol. Plant Pathol. 2010;11:829–846. doi: 10.1111/j.1364-3703.2010.00648.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opgen-Rhein R., Strimmer K. From correlation to causation networks: a simple approximate learning algorithm and its application to high-dimensional plant gene expression data. BMC Syst. Biol. 2007;1:37. doi: 10.1186/1752-0509-1-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer J., Strimmer K. An empirical bayes approach to inferring large-scale gene association networks. Bioinformatics. 2005a;21:754–764. doi: 10.1093/bioinformatics/bti062. [DOI] [PubMed] [Google Scholar]
- Schäfer J., Strimmer K. A shrinkage approach to large-scale covariance matrix estimation and implications for functional genomics. Stat. Appl. Genet. Mol. Biol. 2005b;3:32. doi: 10.2202/1544-6115.1175. [DOI] [PubMed] [Google Scholar]
- Sønderby I.E., et al. Biosynthesis of glucosinolates - gene discovery and beyond. Trends Plant Sci. 2010;15:283–290. doi: 10.1016/j.tplants.2010.02.005. [DOI] [PubMed] [Google Scholar]
- Taylor L.P., Grotewold E. Flavonoids as developmental regulators. Curr. Opin. Plant Biol. 2005;8:317–323. doi: 10.1016/j.pbi.2005.03.005. [DOI] [PubMed] [Google Scholar]
- Teng S.L., Huang H. A statistical framework to infer functional gene relationships from biologically interrelated microarray experiments. J. Am. Stat. Assoc. 2009;104:465–473. [Google Scholar]
- Verkerk R., et al. Glucosinolates in Brassica vegetables: the influence of the food supply chain on intake, bioavailability and human health. Mol. Nutr. Food. Res. 2009;53(Suppl. 2):S219. doi: 10.1002/mnfr.200800065. [DOI] [PubMed] [Google Scholar]
- Wille A., et al. Sparse graphical Gaussian modeling of the isoprenoid gene network in Arabidopsis Thaliana. Genome Biol. 2004;5:R92. doi: 10.1186/gb-2004-5-11-r92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wille A., Bühlmann P. Low-order conditional independence graphs for inferring genetic networks. Stat. Appl. Genet. Mol. Biol. 2006;5:1. doi: 10.2202/1544-6115.1170. [DOI] [PubMed] [Google Scholar]
- Woo H., et al. Flavonoids: from cell cycle regulation to biotechnology. Biotechnol. Lett. 2005;27:365–374. doi: 10.1007/s10529-005-1521-7. [DOI] [PubMed] [Google Scholar]
- Yan X., Chen S. Regulation of plant glucosinolate metabolism. Planta. 2007;226:1343–1352. doi: 10.1007/s00425-007-0627-7. [DOI] [PubMed] [Google Scholar]
- Yonekura-Sakakibara K., et al. Comprehensive flavonol profiling and transcriptome coexpression analysis leading to decoding genemetabolite correlations in arabidopsis. Plant Cell. 2008;20:2160–2176. doi: 10.1105/tpc.108.058040. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.