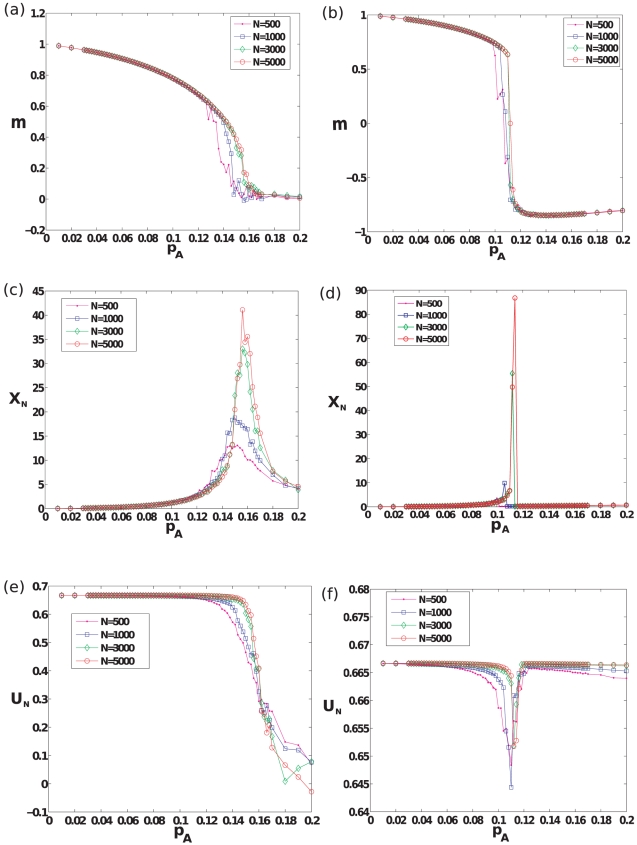
Figure 2. Behavior of typical order parameters as a function of linear trajectories of slope that pass through the origin, in parameter space for a complete graph.

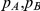(a)–(b) Steady-state magnetization defined in the text, for successive pairs along lines of slope 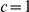and 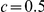respectively that pass through the origin. The 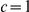line in parameter space passes through the cusp point and gives rise to a second-order phase transition, while the 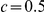line passes through a point on the (right) bifurcation line giving rise to a first-order phase transition. Here 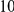realizations of social influence dynamics were performed for each 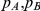pair, starting from the initial condition 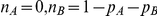, and the magnetization was measured conditioned on the system remaining in the steady state that it initially converged to. 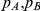(c)–(d) Binder cumulant defined in the text for successive pairs along lines of slope 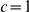and 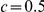respectively, that pass through the origin. (e)–(f) Scaled variance, 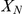, defined in the text for successive 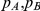pairs along lines of slope 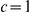and 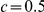respectively, that pass through the origin. Data for (c),(d),(e) and (f) were generated from 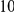realizations of the social influence dynamics, per 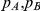pair, for each of two initial conditions: 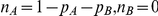and 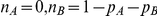.