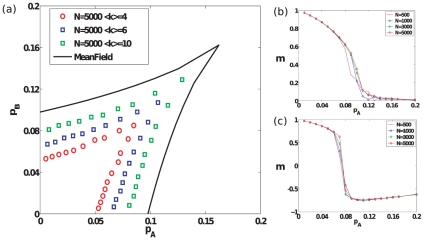
Figure 5. Results for Erdös-Rényi random graphs.
(a) The bifurcation lines and cusp point in parameter space obtained through simulations of Erdös-Rényi random graphs of size 
with different average degrees. The mean-field analytical curve is shown for comparison. For simulation results, the bifurcation curves are obtained by identifying the critical points that lie on linear trajectories described by 
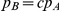in parameter space. This process is carried out for different values of 
between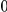 
and 
at intervals of 
, and for each value of 
, 
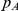is varied at a resolution of 
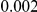. For each such combination of 
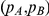obtained, we perform averages for quantities of interest over 
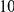realizations of networks (with a single realization of the social influence dynamics per network), for each of two initial conditions, 
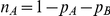and 
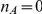with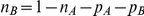 
in each case. (b)–(c) Steady-state magnetization for ER graphs with 
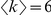and different sizes 
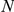, as parameter pair values are varied successively along slope 
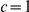and slope 
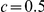lines in parameter space respectively.