A Limited Sampling Schedule to Estimate Mycophenolic Acid Area Under the Concentration-Time Curve in Hematopoietic Cell Transplantation Recipients

Abstract

Mycophenolate mofetil (MMF) is a key component of post-grafting immunosuppression in hematopoietic cell transplant (HCT) recipients. The plasma area under the curve (AUC) of its active metabolite, mycophenolic acid (MPA), is associated with MMF efficacy and toxicity. This study developed a population pharmacokinetic model of MPA in HCT recipients and created limited sampling schedules (LSS) to enable individualized pharmacotherapy. A retrospective evaluation of MPA concentration-time data following a 2 hr MMF intravenous (IV) infusion was conducted in 77 HCT recipients. The final model consisted of one and two compartments for MMF and MPA pharmacokinetics, respectively. The mean estimated values (coefficient of variation, %) for total systemic clearance, distributional clearance, and central and peripheral compartment volumes of MPA were 36.9 L/h (34.5%), 15.3 L/h (80.4%), 11.9 L (71.7%), and 182 L (127%), respectively. No covariates significantly explained variability among individuals. Optimal LSS were derived using a simulation approach based on the scaled mean squared error. A five-sample schedule of 2, 2.5, 3, 5, and 6 hr from the start of the infusion precisely estimated MPA AUC_{0–12 hr} for Q12 hr IV MMF. A comparable schedule (2, 2.5, 3, 4 and 6 hr) similarly estimated MPA AUC_0–8hr for Q8 hr dosing.

Introduction

Allogeneic hematopoietic cell transplantation (HCT) offers curative treatment for hematologic diseases.¹ An integral component of this procedure is post-grafting immunosuppression, administered after the allogeneic donor graft has been infused. The combination of a calcineurin inhibitor (cyclosporine or tacrolimus) and mycophenolate mofetil (MMF) has an established use in post-grafting immunosuppression in both nonmyeloablative^2–3 and myeloablative HCT.^4–6

After administration, the prodrug MMF is rapidly hydrolyzed to mycophenolic acid (MPA).⁷ MPA selectively and reversibly inhibits inosine monophosphate dehydrogenase (IMPDH), subsequently blocking the de novo pathway of purine synthesis in T and B lymphocytes.⁷ In allogeneic HCT recipients, the current method of dosing MMF based on body weight leads to considerable interpatient variability in the pharmacodynamics (i.e., the efficacy and toxicity) and the pharmacokinetics of MPA. Notably, the plasma MPA half-life is shorter in allogeneic HCT recipients (0.6 to 3.6 hr)⁶ than in solid organ transplant patients (9 to 17 hr).⁷ MPA undergoes hepatic metabolism with biliary excretion as the pharmacologically inactive MPA 7-O-glucuronide. MPA 7-O-glucuronide is converted back to MPA by β-glucuronidase enzyme by the gastrointestinal track flora.⁷ MPA is then reabsorbed (enterohepatic recycling), leading to a secondary peak in the concentration-time profile. In solid organ transplant recipients, the secondary peak accounts for 40% (range 10% – 60%) of the total MPA AUC over a dose-interval (i.e., AUC_0-τ).⁷ Allogeneic HCT recipients have a lower prevalence of a delayed second peak,⁶ presumably resulting from reduced enterohepatic circulation. Various mechanisms have been proposed for this pharmacokinetic difference between these patient populations. Reduced enterohepatic circulation of MPA glucuronide may result from mucosal damage caused by radiation or high-dose chemotherapy doses of myeloablative conditioning and/or the reduction in bacterial flora in the gastrointestinal tract from broad-spectrum antibiotic use. Furthermore, MMF is often combined with cyclosporine, which inhibits excretion of glucuronidated MPA by multi-drug resistance protein 2 (MRP2, or ATP binding cassette protein C2). This subsequently reduces the enterohepatic circulation of MPA glucuronide back to MPA.⁷

The available pharmacodynamic data in allogeneic HCT recipients suggest that the relationship between MPA concentration and clinical outcomes may differ based on the conditioning regimen and/or graft source. In patients undergoing nonmyeloablative conditioning with an unrelated donor graft, we have demonstrated that less frequent (i.e., Q12 hr) MMF dosing and low total MPA plasma area under the concentration-time curve (AUC) are related to a higher risk of graft rejection.^8–9 Thus, in this subset of allogeneic HCT recipients, MMF is administered every 8 hr to achieve AUCs similar to those in solid organ transplant patients.³ Low total MPA AUC is also related to low (<50%) T cell donor chimerism, but no significant association was observed between total or unbound MPA AUC and acute GVHD or relapse.⁹ MPA AUC or predose concentrations have also been associated with clinical outcomes in patients receiving fludarabine/cyclophosphamide conditioning regimens and cord blood grafts.^10–11 Personalizing MMF doses based on MPA AUC has been proposed by some HCT centers.¹² First, however, further studies in homogenous HCT populations are needed.

Population pharmacokinetic models are key tools for elucidating pharmacodynamic relationships in HCT recipients. These models provide a quantitative approach to characterizing the time-course of net drug exposure and to identifying the patient characteristics or covariates that explain variance in the model parameters used to determine individual AUC values. Subsequently, a population model can be used in conjunction with sparse concentration-time data to estimate individual patient AUC values without difficult, frequent, and invasive pharmacokinetic sampling. The creation of a population pharmacokinetic model and limited sampling schedule (LSS) can greatly facilitate the identification of pharmacodynamic relationships in homogenous HCT populations and the use of kinetics-based MMF dosing to achieve the target total MPA AUC associated with optimal clinical outcomes.

Thus, in this analysis, we sought to create a population pharmacokinetic model for total MPA concentrations in HCT patients who received intravenous (IV) MMF. We also evaluated covariates associated with MPA pharmacokinetics, with the aim of further understanding factors influencing the time-course of MPA exposure in allogeneic HCT recipients. Finally, we sought to create a LSS to be used in ancillary biomarker studies in both inpatient and outpatient HCT recipients.

Materials and Methods

Patients and sampling design

Pharmacokinetic data were collected from 77 allogeneic HCT recipients who underwent HCT for a variety of hematologic malignancies between 1999 and 2006 at the Fred Hutchinson Cancer Research Center (Seattle, WA). Written informed consent was obtained from all patients; study protocols were approved by the Institutional Review Board at the Fred Hutchinson Cancer Research Center and monitored by an independent Data Safety Monitoring Board. MMF and a calcineurin inhibitor (either cyclosporine or tacrolimus) were given as post-grafting immunosuppression. Patients received MMF 15 mg/kg Q6, Q8, or Q12 hr by 2 hr IV infusion; the MMF dose was based on adjusted ideal body weight (AIBW). The first dose of IV MMF was administered at least 2 hr after the end of the hematopoietic cell infusion. The pharmacokinetic blood samples were obtained at 0, 1, 2, 4, 6, 8, and 10 hr for the Q 12 hr dosing regimen and at 0, 1, 2, 4, 6, and 8 hr in group B for the Q 8 hr dosing regimen.⁶ 166 total MPA AUCs were collected among the following occasions: week 0 (day 0 – day 1), week 1 (day 6 – day 9), week 2 (day 13 – day 16), week 3 (day 20 – day 24), week 4 (day 26 – day 28), and 2–9 months post transplantation. For each AUC calculation, between four and seven pharmacokinetic samples were collected during one dosing interval; most patients had five to six pharmacokinetic samples, including one pre-dose measurement. Total MPA plasma concentration was quantified using reverse-phase high performance liquid chromatography (HPLC) with UV detection as previously described.⁹ The dynamic range was 0.2 to 30 μg/mL and the inter-day coefficient of variation was less than 10%.

Population pharmacokinetic analysis

Total MPA plasma concentration-time data were analyzed using nonlinear mixed effect modeling (NONMEM^® VI; Icon Development Solutions, LLC, Ellicott City, MD, USA). The first-order conditional estimation method with interaction (FOCEI) was used throughout the modeling process. MMF doses were converted to the equivalent MPA content by multiplying by 0.739.⁷

Structural model

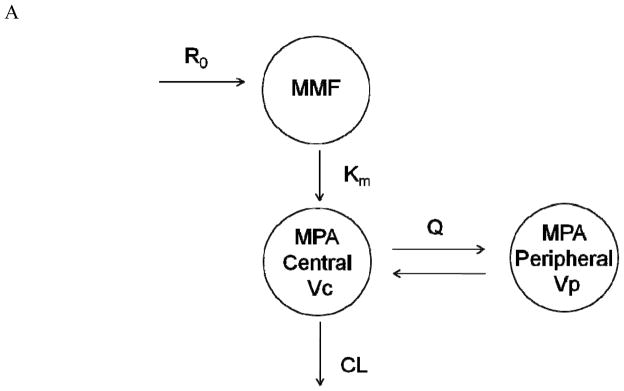
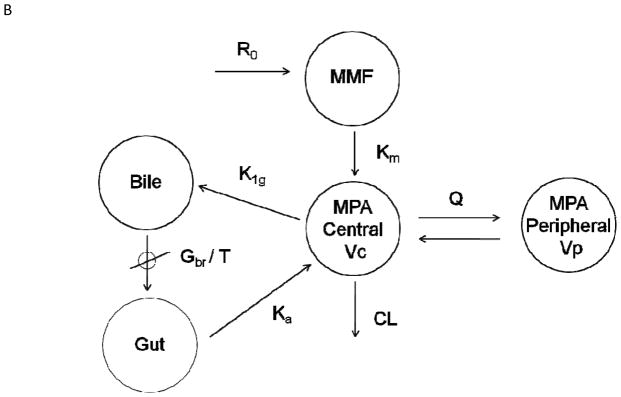
Two structural pharmacokinetic models were tested. The first model consisted of one compartment for MMF kinetics and two compartments with first-order elimination for MPA (Figure 1A) and was parameterized in terms of a first-order MMF metabolic rate constant (k_m), MPA clearance (CL), central and peripheral volumes of MPA distribution (V_c, V_p), and inter-compartmental clearance of MPA (Q). This structure was extended in the second model to include additional compartments (bile and gut compartments) to account for enterohepatic cycling of MPA (Figure 1B). A log normal distribution was assumed on inter-individual variability (IIV, also referred to as between-subject variability or BSV) and inter-occasion variability (IOV, also referred to as between-occasion variability or BOV). Individual pharmacokinetic parameters were modeled using an exponential error model:

$${\text{P}}_{\text{ij}}={\text{P}}_{\text{pop}}\times exp({\eta }_{\text{i}}+{\kappa }_{\text{j}})$$ (Eq. 1)

Figure 1.

Schematic of pharmacokinetic models used to describe total MPA concentration time course following 2 hr IV infusion of MMF: one compartment model for IV MMF pharmacokinetics and two compartments with first-order elimination for MPA (1A), and an extension including additional compartments (i.e., bile and gastrointestinal or GI) of enterohepatic cycling (1B). R₀ = zero-order IV infusion rate constant; k_m = first-order metabolizing rate constant; CL = clearance; V_c = volume of central compartment of MPA; Q = inter-compartment clearance; V_p = volume of peripheral compartment of MPA; k_1g = first-order order rate constant of drug excreted into bile; G_br = zero-order release bile from gallbladder into GI tract; T = bile emptying interval; k_a = first-order rate constant for absorption from GI tract.

(Eq. 1) where P_ij is the parameter value for the i^th individual on the j^th occasion, and P_pop is the population mean for pharmacokinetic parameter P (e.g., CL). η_i and κ_j represent differences from P_pop among individuals and among occasions, with a mean of zero and variance of ω² and π², respectively. The covariance between inter-individual random effects was estimated using a full variance-covariance matrix. Residual variability was modeled with additive, proportional, or additive plus proportional error models:

$${\text{Y}}_{\text{ijk}}={\text{IPRE}}_{\text{ijk}}\times (1+{\epsilon }_{1\text{ijk}})+{\epsilon }_{2\text{ijk}}$$ (Eq. 2)

where Y_ijk represents the observed concentration and IPRE_ijk is the predicted concentration for the i^th individual on the j^th occasion at the k^th sampling time. ε_ijk terms were assumed to follow a normal distribution with a mean of 0 and variance of σ². Model selection was based on objective function values (OFV), precision of parameter estimates, goodness-of-fit (GOF) plots, and visual predictive check (VPC) plots. GOF plots included observed versus predicted concentrations, as well as weighted residuals (WRES) versus predicted values and time post dose. Diagnostic graphics were generated in S-PLUS 8.0 (Insightful Corp., Seattle, WA, USA).

Covariate analysis

Relationships between pharmacokinetic parameters and patient characteristics and clinical laboratory tests were investigated to evaluate IIV of pharmacokinetic parameters. The following covariates were analyzed: gender, age, AIBW, height, body surface area (BSA), type of conditioning (nonmyeloablative vs. myeloablative), fludarabine administration (yes vs. no), donor type (HLA-matched related vs. unrelated), concomitant calcineurin inhibitor (cyclosporine vs. tacrolimus), serum creatinine, creatinine clearance (estimated using weight-adjusted Cockcroft-Gault equation), alanine aminotransferase (ALT), aspartate aminotransferase (AST), alkaline phosphatase (ALK), lactate dehydrogenase (LDH), total bilirubin, direct bilirubin, and serum albumin. Biochemistry values were obtained within the seven days before MPA pharmacokinetic sampling. If no value was available within one week, the missing value was replaced by the population median.¹³ More than 10% of ALT, LDH, ALK, and direct bilirubin data were missing; 1.2% of AST data were missing. Individual Bayesian estimates of pharmacokinetic parameters were obtained from the structural model by using the ‘POSTHOC’ option in NONMEM. Scatter plots of individual Bayesian estimates versus covariates were generated to visually inspect for relationships between pharmacokinetic parameters and covariates.

Covariate model building followed a standard two-step approach of stepwise forward selection and backward elimination. The covariates evaluated are listed in Table I. In the first step (forward selection), all covariates were introduced into the structural model separately. Inclusion of a covariate was determined by the likelihood ratio test and a reduction in unexplained IIV. For the likelihood ratio test, the difference in OFV between a model with and without a covariate is approximately χ² distributed with degrees of freedom equal to 1. A decrease of at least 6.6 in the OFV (p<0.01) was considered to be statistically significant. In the second step (backward elimination), all covariates selected in the first step were excluded one by one from the intermediate model. A covariate was retained in the final model if an increase of at least 10.8 (p<0.001) in the OFV occurred after excluding the covariate.

Table I.

Characteristics of HCT Recipients^a

Number of participants	77
Demographic characteristics
Gender (male/female)	46/31
Age (year)	45 [18–73]
Adjusted ideal body weight (kg)	70.9 [42.2–95.0]
Height (cm)	172.0 [82.9–191]
Body surface area (m2)	1.92 [1.30–2.59]
HCT characteristics
Type of conditioning
Nonmyeloablative	17
Myeloablative	60
Fludarabine administration (yes/no)	16/61
Donor type (HLA-matched related/unrelated)	58/19
Concomitant calcineurin inhibitor
Tacrolimus	24
Cyclosporine	53
Biochemistryb
Serum creatinine (mg/dL)	0.8 [0.3–5.7]
Creatinine clearance (ml/min)	92 [46.7–159]
Serum alanine aminotransferase (U/L)	23 [8–717]
Serum aspartate aminotransferase (U/L)	20 [7–204]
Serum alkaline phosphatase (U/L)	68 [30–366]
Serum lactate dehydrogenase (U/L)	190 [87–1697]
Serum total bilirubin (μmol/L)	0.9 [0.2–37.5]
Serum direct bilirubin (μmol/L)	0.2 [0.1–23.7]
Serum albumin (g/dL)	3 [1.7–3.9]

^acategorical data presented as number of participants meeting stated criteria; continuous data presented as median [min-max];

^bobtained within the seven days before MPA pharmacokinetic sampling

Continuous covariates, such as AIBW, were centered to their median and relationships with pharmacokinetic parameters, P, were defined as:

$${\text{P}}_{\text{i}}={\text{P}}_{\text{pop}}\times {({\text{AIBW}}_{\text{i}}/{\text{AIBW}}_{\text{med}})}^{\theta }\text{AIBW}$$ (Eq. 3)

where P_pop is the population value of parameter P for an individual (i) with median AIBW. θ_AIBW is an exponent determining the shape of the relationship between AIBW and parameter P. Categorical covariates, such as gender, were tested in the model according to:

$${\text{P}}_{\text{i}}={\text{P}}_{\text{pop}}\times {\theta }^{\text{gender}}$$ (Eq. 4)

where P_pop is the population value of parameter P for males (for females, gender = 1 and for males, gender =0) and θ is the ratio of parameter P in females to males. The effect of concomitant medication (cyclosporine or tacrolimus) was tested on CL:

$${\text{CL}}_{\text{i}}={\text{CL}}_{\text{pop}}+{\theta }_{\text{cyclosporine}}$$ (Eq. 5)

where CL_pop is the population mean CL for patients co-medicated with tacrolimus and θ_cyclosporine is the change in CL for patients co-medicated with cyclosporine.

Model qualification

The predictive performance of the final model was internally qualified using VPC plots. 500 data sets were simulated from parameter estimates of the final model. 5^th, 50^th, and 95^th percentiles of simulated data were compared with observed data. In addition, bootstrapping was conducted using algorithms implemented in Wings for NONMEM VI (http://wfn.sourceforge.net/index.html). 200 bootstrap data sets were generated by nonparametric sampling from the original dataset with replacement. Parameters were estimated for each bootstrap data set using the final model. The performance of the model was evaluated by comparing the median and 95% confidence interval (2.5%–97.5% percentiles) of the parameter estimates of the bootstrap data sets with that of the original data set.

LSS development for estimating AUC values

Optimal LSSs were determined separately for Q8 hr and Q12 hr IV MMF dosing regimens, where 1000 mg of MMF (~ 1050 mg = 15 mg/kg MMF dose for a 70 kg patient) is administered over a 2 hr IV infusion. To minimize patient inconvenience, the optimal LSSs were designed to include no more than five samples, which would be obtained within 6 hr after the end of the 2 hr IV infusion. Optimal sampling times were selected from the time set of 2, 2.5, 3, 4, 5, 6, 7, and 8 hr from the start of infusion, as well as one pre-dose time point (time = −0.1hr). LSSs were developed for both non-steady-state (day 2, 4^th dose for Q12 hr and 5^th dose for Q8 hr) and steady-state (day7, 14^th dose for Q12 hr and 20^th dose for Q8 hr) conditions.

Optimal LSSs were determined by a simulation approach that was described previously.¹⁴ Briefly, based on the population pharmacokinetic model of MPA described above, MPA concentration-time curves for 1000 virtual subjects were simulated; individual pharmacokinetic parameters followed a log normal distribution with a mean and variance equal to the estimated population values, P_pop and ω², respectively. Each simulated subject’s MPA time-course was replicated 15 times with different simulated residual errors to account for unknown residual variability (e.g., assay error, error in sampling times, etc.). For each potential LSS, maximum a posteriori (MAP) Bayesian estimates of pharmacokinetic parameters were obtained from the MPA concentration-time profile of each virtual subject at each replicate using the ‘POSTHOC’ and MAXEVAL=0 options in NONMEM. Predicted AUC values (AUC_0–12hr for Q12 hr dosing and AUC_0–8hr for Q8 hr dosing) were calculated based on MAP Bayesian estimates and were compared with the true (simulated) AUC values, which were computed using the ODE solver in NONMEM to integrate the AUC from 0–8 or 0–12 hr. A scaled mean square error (sMSE) was computed to assess the agreement between the predicted AUC calculated based on data from the LSS and the true AUC:

$$\begin{array}{l}{\mathit{MSE}}_j={(\frac{1}{N}\sum _{i=1}^N({\mathit{AUC}}_{ij}^{\mathit{pred}}-{\mathit{AUC}}_j^{\mathit{true}}))}^2+\frac{1}{N}\sum _{i=1}^N{({\mathit{AUC}}_{ij}^{\mathit{pred}}-\frac{1}{N}\sum _{i=1}^N{\mathit{AUC}}_{ij}^{\mathit{pred}})}^2\\ ={\mathit{Bias}}^2+\mathit{Variance}\end{array}$$ (Eq. 8)

$${\mathit{sMSE}}_j={\mathit{MSE}}_j/{({\mathit{AUC}}_j^{\mathit{true}})}^2$$ (Eq. 9)

where MSE_j and sMSE_j were calculated for the j^th simulated subject, N=15 are the 15 residual variability replicates for the j^th subject, ${\mathit{AUC}}_{ij}^{\mathit{pred}}$ is the predicted AUC from the LSS for each residual variability replicate i of the j^th subject, and ${\mathit{AUC}}_j^{\mathit{true}}$ is the true (simulated without error) AUC of the j^th subject. The LSS producing the minimum mean sMSE (across all virtual subjects) was considered optimal. The square root of the mean sMSE (so-called RMSE) was calculated as:

$$\mathit{Root}\mathit{Mean}\mathit{sMSE}=\sqrt{\frac{1}{M}\sum _{j=1}^M{\mathit{sMSE}}_j}$$ (Eq. 10)

The root mean sMSE was calculated across 1000 simulated subjects (M = 1000). In addition to the Pearson correlation coefficient (r), the mean relative bias (r_bias), one component of MSE, was also computed as an assessment of the performance of the LSS:

$$\mathit{mean}\mathit{relative}\mathit{bias}\%=\frac{1}{M}\sum _{j=1}^M\frac{\sqrt{{(\frac{1}{N}{\displaystyle \sum _{i=1}^N}({\mathit{AUC}}_{ij}^{\mathit{pred}}-{\mathit{AUC}}_j^{\mathit{true}}))}^2}}{{\mathit{AUC}}_j^{\mathit{true}}}\times 100$$ (Eq. 11)

Comparisons between the optimal LSS and the reference design were conducted for the 1000 simulated subjects (each subject’s time-course was averaged across the 15 residual variability replicates). The reference design included sampling prior to and at 1, 2, 4, 6, 8, and 10 hr after the morning dose for the Q12 hr dosing regimen. An identical reference design was specified for the Q8 hr regimen, with exclusion of the 10 hr sample. Simulations and statistical analysis were performed in the open-source statistical software R with parameter estimation conducted via system calls to NONMEM.

Results

Population pharmacokinetic model

In total, 166 MPA concentration-time profiles (955 concentration-time measurements) were obtained from 77 allogeneic HCT recipients. Fifty of the 77 participants were enrolled in clinical trials evaluating the efficacy of IV MMF and a calcineurin inhibitor (either cyclosporine⁶ or tacrolimus) as post-grafting immunosuppression. The remaining 27 patients were enrolled on various protocols that stipulated pharmacokinetic sampling after MMF administration. Patient characteristics and biochemistry values are summarized in Table I. As described above, two structural models were evaluated; the simpler model, with one and two compartments for MMF and MPA pharmacokinetics, respectively, adequately described the data and was selected as the final model (Figure 1A). Plots of individual model predicted versus observed MPA concentrations showed satisfactory agreement (Supplemental Figure 1). Individual weighted residuals (IWRES) were evenly distributed on both sides of the identity line (IWRES = 0), although a slight trend was observed during the third treatment occasion (Supplemental Figure 2). The enterohepatic cycling model could not be identified using the available data. This agrees with only eight AUCs (each from a different patient) having a secondary peak after visual inspection of the MPA concentration-time profile. Population parameter estimates of the final model are summarized in Table II. Most parameters were estimated with reasonable precision: RSE% was less than 30% except for IIV on the first-order MMF metabolic rate constant (k_m) and on the volume of the central compartment (V_c). Introduction of inter-occasion variability into the model did not improve its performance in terms of the precision of parameter estimates and standard diagnostics and hence was excluded from the final model. The median terminal elimination estimate was 11.9 hr in these HCT patients. Shrinkage estimates were calculated based on the empirical Bayesian estimates of η and IWRES,¹⁵ and the η-shrinkage of CL, V_c, Q, V_p, and k_m were 9.0%, 36.8%, 18.6%, 26.0%, and 31.7%, respectively. The ε-shrinkage was 7.7%.

Table II.

Final total MPA pharmacokinetic parameter estimates in HCT recipients receiving IV MMF

Pharmacokinetic Parameter	Explanation	Estimate [RSE%a]	Bootstrap Analysis
			Median	95% CI [2.5th–97.5th percentile]
km (1/h)	First-order metabolizing rate constant of MMF to MPA	1.69 [14.4]	1.70	[1.46 – 2.60]
CL (L/h)	MPA clearance	36.9 [5.4]	36.4	[34.1 – 39.5]
Vc (L)	Volume of central compartment	11.9 [46.0]	11.3	[4.79 – 22.8]
Q (L/h)	Intercompartmental clearanceb	15.3 [12.9]	15.2	[12.4 – 18.7]
Vp (L)	Volume of peripheral compartment	182 [16.9]	200	[122– 300]
Inter-individual variability
η km (CV%)		17.0 [219.7]	24.9	[4.02 – 54.0]
η CL (CV%)		34.5 [25.0]	34.1	[28.5 – 39.5]
η Vc (CV%)		71.7 [114.2]	70.5	[40.2 – 131.1]
η Q (CV%)		80.4 [33.5]	79.9	[64.2 – 97.3]
η Vp (CV%)		127.3 [34.1]	127.5	[88.0 – 165.0]
Proportional error (CV%)		44.5 [9.2]	44.5	[36.9 – 49.0]
Additive error (mg/L)		0.10 [23.1]	0.09	[0.032 – 0.17]

^aRSE = relative standard error; CV = coefficient of variation;

^bbetween central and peripheral compartment;

^cmedian half-life estimate was 11.9 hr

Covariate analysis

The final model did not include any of the covariates which were investigated in this current study (listed in Table I). The change in OFV values during forward step-wise covariate selection and backward elimination is shown in Supplemental Table I. Body surface area (BSA) was slightly correlated with CL (Pearson r = 0.24; p<0.05) and V_c (Pearson r = 0.22; p<0.1). In the forward selection step, inclusion of BSA as a covariate to CL resulted in a significant improvement in the OFV and slight decrease in IIV of CL (1.6%) but not V_c. Inclusion of AIBW as a covariate to CL decreased OFV greater than 6.6 unit and IIV of CL by 0.9%. However, neither BSA nor AIBW were retained in the backward elimination step. Exclusion of either BSA or AIBW caused an increase of OFV less than 10.8 units. No correlation was found between other model parameters and AIBW.

Adding albumin as a covariate to the intercompartmental clearance (Q) resulted in a 20 unit decrease in the OFV and a 7.5% decrease in the IIV of Q. Introduction of albumin as a covariate on CL did not decrease the IIV of CL although the OFV decreased 8.4 units (p <0.01). Therefore, the association of albumin with Q but not CL indicated this covariate was not fully supported within the pharmacokinetic model, so it was not included in the final model. No significant correlation could be found between MPA CL and the use of cyclosporine versus tacrolimus.

Model qualification

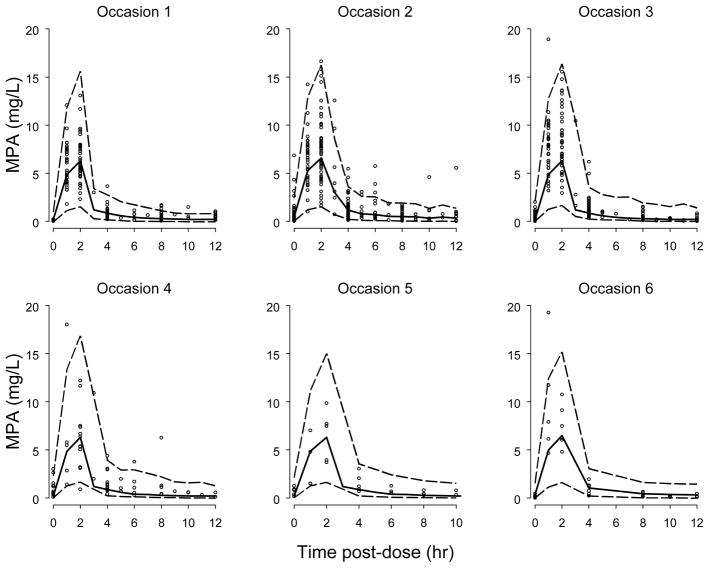
The predictive performance of the final model was assessed using VPCs and bootstrap analysis. As shown in Figure 2, the final model adequately characterized the observed data. The results of 200 bootstrap runs are presented in Table II. The median of the pharmacokinetic parameter estimates resulting from the 198 successful bootstrap runs compared favorably with the estimates of the final model (Table II).

Figure 2.

Visual predictive check for total MPA concentration-time data in HCT recipients. Open circles represent observed data, solid lines represent the 50^th percentile of simulated concentrations, and dashed lines represent the 5^th and 95^th percentiles of the simulated data. Occasions 1 – 6 correspond to week 0 (day 0–day 1), week 1 (day 6–day 9), week 2 (day 13–day 16), week 3 (day 20–day 24), week 4 (day 26–day 28), and 2–9 months post transplantation.

MAP Bayesian-based LSS

The root mean sMSE of the ten best five-sample LSSs for non-steady-state and steady-state conditions for the Q12 hr IV MMF dosing regimen are listed in Supplemental Table I. These sampling designs demonstrated similar overall performance. The 2, 2.5 and 3 hr time points were present in all of the ten best five-sample LSSs, indicating that these points were highly informative. A sampling schedule at 2, 2.5, 3, 5, and 6 hr after the start of MMF infusion provided the lowest root mean sMSE on AUC_0–12hr for sampling at both the 4^th (non-steady-state) and 14^th doses (steady-state). This design was determined to be the optimal five-sample LSS for Q12 hr IV MMF dosing based on the low root mean sMSE and on the shorter sampling duration.

Various alternative LSSs (i.e., three- and four-sample designs) were also developed and compared to the five-sample LSS and the reference design (Table III). Optimal four- and five-sample schedules performed favorably when compared with the reference design for the purpose of estimating individual exposure (i.e. AUC_0–12hr) in terms of sMSE, Pearson correlation coefficient (r), mean relative bias (r_bias) %, and the percentage of patients with a relative bias greater than 10%. Predicted AUC_0–12hr values for 100 simulated subjects (each subject was averaged across 15 residual variability replicates) were compared to the true AUC_0–12hr (Supplemental Figure 3). The optimal four- and five-sample LSSs provided accurate estimation of AUC_0–12hr, although a bias is observed leading to slight under-prediction of AUC_0–12hr for high values. Compared to the five-sample LSS, the three-sample LSS showed a slightly inferior performance, as evidenced by the higher root mean sMSE, higher relative bias, and higher percentage of patients with a relative bias greater than 10%.

Table III.

Comparison between optimal LSS and reference design for estimating AUC^a_0-τ after IV MMF dosing

	Sampling time (hr)	Root mean sMSEb % (AUC0-τ)	Mean relative bias (rbias)% (AUC0-τ)	Pearson r	Percent of subjects with rbias% > 10%
Q 12 hr MMF dosing
Reference design	Pre-dose, 1, 2, 4, 6, 8, 10	17.62	9.19	0.97	1.7%
5-sample LSS	2, 2.5, 3, 5, 6	17.37	9.03	0.97	1.5%
4-sample LSS	2, 2.5, 3, 6	18.50	9.78	0.97	1.2%
3-sample LSS	2, 2.5, 5	20.56	10.8	0.97	3.2%
Q 8 hr MMF dosing
Reference design	Pre-dose, 1, 2, 4, 6, 8	18.37	10.0	0.97	1.7%
5-sample LSS	2, 2.5, 3, 4, 6	17.36	9.29	0.97	1.5%
4-sample LSS	2, 2.5, 3, 5	18.18	9.59	0.97	1.3%
3-sample LSS	2, 2.5, 5	20.30	11.0	0.98	2.5%

^aAUC_0-τ where τ is dosing frequency, so AUC_0-12hr for IV MMF dosed Q12 hrs and AUC_0-8hr for IV MMF dosed Q8hrs;

^bsMSE: scaled mean square error.

The same methodology was applied to develop the optimal LSS for the Q8 hr regimen; the results are shown in Table III and Supplemental Figure 4. A five-sample design including samples at 2, 2.5, 3, 4, and 6 hr resulted in comparable or improved predictive performance relative to the reference design (e.g., pre-dose, 1, 2, 4, 6, 8 hr) for estimating AUC_0–8hr. The optimal four- and five-sample LSSs provided accurate estimation of AUC_0–8hr, although a bias is observed leading to slight under-prediction of AUC_0–8hr for high values. The three-sample LSS did have a slightly inferior performance, as evidenced by the higher root mean sMSE, higher relative bias, and higher percentage of patients with a relative bias greater than 10% compared to the five-sample LSS.

Discussion

MPA is increasingly used for prophylaxis and treatment of GVHD after solid organ or allogeneic hematopoietic cell transplantation. As a result of large between-subject variability and a narrow therapeutic index, therapeutic drug monitoring (TDM) of MPA in HCT recipients may be recommended to maximize its immunosuppressive effect while minimizing adverse events (e.g., cytopenias or cytomegalovirus reactivation).⁷ Although the pharmacokinetics of MPA are well characterized in solid organ transplant recipients, this study represents the first population pharmacokinetic model in HCT patients who received IV MMF. The population pharmacokinetic models and therapeutic drug monitoring methodology for MPA in solid organ transplant patients are not immediately applicable to HCT recipients, who have a decreased MPA AUC and a shorter half-life.⁶ The present study also sought to identify covariates associated with MPA pharmacokinetics and to develop population pharmacokinetic-based LSSs. Our MPA pharmacokinetic dataset was obtained from various clinical studies in HCT recipients, predominantly phase I/II trials evaluating the pharmacokinetics and toxicity of IV MMF as acute GVHD prophylaxis.

The pharmacokinetic profile of MPA is bi-exponential, and a two-compartmental model with first-order elimination was found appropriate to describe its disposition (Figure 1A). The single compartment with first-order metabolism of MMF (k_m) represents the process of MMF hydrolysis to MPA in the blood. Few (8) of the AUCs exhibited a secondary peak, consistent with enterohepatic circulation, and it was not unexpected that the current data did not collectively support such a model (Figure 1B). Reduced enterohepatic circulation in HCT recipients has been reported;⁶ this has been hypothesized to result from mucosal damage due to radiation or high-dose chemotherapy. This hypothesis, however, is not supported by our covariate analysis; the type of conditioning was not a covariate in our population pharmacokinetic model. A recent population pharmacokinetic analysis of MPA in patients with varying diseases (19 renal transplant, 38 HCT, and 36 autoimmune disease patients) found that the underlying diagnosis was not a covariate. MPA clearance was associated with cyclosporine pre-dose concentration and albumin levels, which could explain the difference in MPA pharmacokinetics between the three disease states.¹⁶ Uniquely, our dataset also contained allogeneic HCT recipients treated with tacrolimus.^16–17 A covariate analysis failed to identify comedication with cyclosporine as a significant covariate on MPA CL, in contrast with prior studies in renal transplant recipients.¹⁸ This might be attributed to the minor contribution of enterohepatic cycling to MPA pharmacokinetics in HCT patients. Unfortunately, MPA glucuronide concentrations were not available to better characterize the enterohepatic cycling of MPA and MPAG in allogeneic HCT recipients. It is possible that cyclosporine, as well as albumin, may be detected as covariates of MPA pharmacokinetics in larger sample sizes or in patients receiving oral MMF.

LSSs are essential tools for pharmacodynamic studies in homogeneously treated HCT recipients. This is especially true for nonmyeloablative HCT recipients, many of whom are treated in an outpatient setting and must remain at the clinic during pharmacokinetic sampling. Therefore, we sought to create a LSS in HCT patients receiving IV MMF. A retrospective analysis using a multiple linear regression approach in 73 adult HCT recipients receiving IV or oral MMF with cyclosporine found a three-point LSS, with sampling at 2, 4, and 6 hr post-dose, to best estimate the AUC_0–12hr after IV MMF administration.¹⁹ The multiple linear regression approach is limited in that it is a heuristic approach that is not based on mechanistic understanding of the dose-exposure pharmacokinetics and pharmacology of MMF. Multiple linear regression is less robust and not very useful in practice, as samples must be drawn at precise times, whereas our MAP Bayesian approach can accommodate slight variations in actual sampling times. Our three-sample LSS of 2, 2.5 and 5 hr post dose for Q12 hr IV MMF differs from the 2, 4, and 6hr post-dose LSS proposed by multiple linear regression analysis.¹⁹

The observed differences in LSSs may be explained by several factors, including differences in MPA pharmacokinetics after IV and oral MMF administration. Differences in the patient populations may also contribute; our covariate analysis could not, however, identify any pharmacologically relevant covariates associated with the pharmacokinetic parameters of MPA. Other sources contributing to differences in our LSSs include: the development of an appropriate pharmacokinetic model relating dose and AUC, as opposed to the use of empirical regression analysis; the LSS methodology, which accounts for both precision and bias as opposed to just precision, as routinely done in D-optimality analyses; and lastly, the varying constraints specified to minimize sample collection and patient inconvenience. The three-sample LSS performed adequately and may be used in pharmacodynamic studies where more pharmacokinetic samples cannot be obtained. Compared to the five-sample LSS, the three-sample LSS leads to only a slight increase in the number of patients having a relative bias greater than 10% (1.7% compared to 0.6%), suggesting that a three-sample LSS could be used without sacrificing accuracy.

In the present study, the optimal sampling design was chosen based on minimum sMSE of AUC_0-τ. The advantage of such an approach is that the AUC determined using a variety of alternative LSS can be compared against “true” AUC values, which are known exactly from the simulated concentration-time curves of virtual patients. The D-optimality criterion, which is based on minimizing a norm (i.e., the determinant) of the covariance matrix of the pharmacokinetic parameter estimates, is often used to determine LSS. Although D-optimality is useful, both in individuals and populations, to obtain the most favorable parameter estimate precision, it does not address the question of systematic bias in the AUC estimate (i.e. outcome accuracy). In a small population of 14 HCT recipients receiving oral MMF with cyclosporine, a LSS was recently estimated based on combining the D-optimality criterion for sampling schedule determination with Bayesian estimators.¹⁷ It is difficult, however, to compare the LSS after oral MMF administration, when the absorption rate of MMF must be accounted for, to our findings in patients receiving IV MMF.

In our analysis, combinations of three, four, or five samples after IV MMF administration were tested for evaluation of Bayesian forecasting of MPA AUC. As might be expected, allocating time points around peak concentration (i.e., end of infusion), in the distribution phase (i.e., 2.5 and 3 hr post dose), and in the elimination phase (i.e., 5 and 6 hr post dose) allows for accurate AUC projections. The four- or five-sample LSSs require fewer blood samples without sacrificing the precision of AUC calculations using the reference sampling design. These LSS cannot be applied to solid transplant patients because of the underlying differences in the MPA concentration-time profile, which are presumably due to differences in the cyclosporine pre-dose concentration and albumin levels between these disease states.¹⁶ In renal transplant recipients, oral MMF doses have been personalized based on estimating an individual’s Bayesian estimates for MPA and a LSS.²⁰ Bayesian estimates of MPA pharmacokinetic parameters using a LSS of 20 minutes, 1 hr, and 3 hr after oral MMF administration had satisfactory accuracy and precision to estimate individual AUCs in renal transplant recipients.^21–22 Within the manuscript, we report the successful development of a population pharmacokinetic model and LSS specific to HCT recipients.

In conclusion, dosing IV MMF based on AIBW appears to be of limited value in decreasing the inter-individual variability in MPA pharmacokinetics although further studies confirming our covariate analysis are needed. Total MPA pre-dose concentrations or AUCs are associated with clinical outcomes in allogeneic HCT recipients.^9–11 Future pharmacodynamic studies can be facilitated by obtaining fewer pharmacokinetic samples. Using a LSS is a practical solution to the problem of projecting MPA AUC values in the absence of rich concentration-time profiles. Three-, four- and five-sample LSSs were developed from both patient data and in a simulation setting; these LSSs enabled accurate estimation of MPA AUCs for HCT recipients. Targeting MPA exposure with a limited number of sampling occasions is desirable for personalizing MPA pharmacotherapy. The developed LSS are clinically applicable, requiring as few as three samples over a 5 or 6 hr time span.